[Wärmeabsorption] [Strahlungsabsorption] [CO2 Einfluss]
Milutin Milanković entwickelt in dieser Publikation eine astronomische Theorie zur Erklärung des periodischen Auftretens von Eiszeiten. Damit die Eiszeiten periodisch auftreten können, müssen zwischen ihnen Warmzeiten auftreten. Das macht die Theorie interessant für eine Erklärung der Klimaerwärmung, die wir gerade diskutieren. Interessanterweise sagt Milanković mit seiner Theorie gerade die stärckere Erwärmung der Polregionen voraus, die die "anthropogene Kohlendioxid Hypothese" nicht erklären kann.
Mit Hilfe der Newton′schen Gravitation leitet Milanković die Bahnbewegungsgleichung der Planeten ab (Nicht die Kepler′sche Gleichung!)
Ich habe die Absätze im Volltext übernommen, die ich mathematisch nachvollziehen kann. Zum Glück habe ich die Grundlagen der sphärischen Trigonometrie, der Infinitesimalrechnung und der Vektorrechnung auf meiner Website bereits dargestellt. Die helfen beim Nachvollziehen der Argumentation Milutin Milanković′s.
Die Ausführungen führen zu ein paar überraschenden Erkenntnissen. Erdbeben und Klimaänderung haben z. B. die gleiche Ursachen: die unregelmäßige Gestalt der Erde.
Kanon der Erdbestrahlung und seine Anwendung auf das Eiszeitproblem
Milutin Milanković
Inhaltsverzeichnis
Kapitel I. Das Newtonsche Gravitationsgesetz
Kapitel II. Das Zweikörperproblem der Himmelsmechanik und die ungestörte heliozentrische Bewegung der Planeten
- § 3. Problemstellung.
- § 4. Die Schwerpunktsintegrale.
- § 5. Die beiden Vektorintegrale der Differentialgleichung der ungestörten heliozentrischen Bewegung der Planeten.
- § 6. Geometrische Deutung der beiden Vektorintegrale.
- § 7. Verschiedene andere Formen der erhaltenen Integrale.
- § 8. Das sechste skalare Integral.
- § 9. Endgültige vektorielle Form der vollständigen Integrale der Differentialgleichung der ungestörten Bewegung der Planeten.
- § 10. Das Satellitenproblem, zurückgeführt auf das Zweikörperproblem.
- § 11. Der Zusammenhang zwischen den vektoriellen und den elliptischen Elementen.
Kapitel III. Die Störungsrechnung
- § 12. Das Mehrkörperproblem der Himmelsmechanik und seine allgemeinen Integrale.
- § 13. Die Differentialgleichungen der hetiozentrischen Bewegung der Planeten.
- § 14. Die vektoriellen Grundgleichungen der Störungsrechnung.
- § 15. Die Klammerausdrücke von Lagrange.
- § 16. Berechnung der Lagrange′schen Klammerausdrücke für die vektoriellen Elemente.
- § 17. Die Gleichungen der zeitlichen Aenderungen der vektoriellen Elemente.
- § 18. Periodische und säkulare Störungen; die Bedeutung dieser letzteren für die Ziele der nachstehenden Forschungen.
- § 19. Die Differentialgleichungen der säkularen Aenderungen der vektoriellen Elemente.
- § 20. Klassische Form der Differentialgleichungen der säkularen Aenderungen der astronomischen Elemente.
- § 21. Die Integration der Differentialgleichungen der säkularen Aenderungen der astronomischen Elemente.
- § 22. Einige Schlussfolgerungen aus den vorstehenden Integralen.
Kapitel IV. Ableitung der für das Studium der Drehbewegungen der Erde erforderlichen Sätze und Gleichungen
- § 23. Das tellurische Massenpunktsystem.
- § 24. Die Impulssätze.
- § 25. Der Schwerpunktsatz.
- § 26. Unabhängigkeit der Drehbewegung von der fortschreitenden Bewegung.
- § 27. Einführung beweglicher Bezugssysteme.
- § 28. Das mit dem bewegten Körper fest verbundene Bezugssystem.
- § 29. Die Eulerschen Winkel.
- § 30. Polhodie und Herpolhodie.
- § 31. Einiges über das Gravitationsfeld raumfüllender Massen.
- § 32. Drehbewegung flüssiger oder gasförmiger Himmelskörper.
- § 33. Drehbewegung mit ausgeglichenen Winkelgeschwindigkeiten.
- § 34. Gleichgewichtsbedingungen.
- § 35. Das Theorem von Clairaut.
Kapitel V. Die tägliche Drehbewegung der Erde und ihre Folgen
- § 36. Mechanismus der kräftefreien Drehbewegung der Erde.
- § 37. Erfahrungstatsachen.
- § 38. Die tägliche Drehbewegung der Erde und ihr Spiegelbild.
- § 39. Sphärische Koordinaten.
- § 40. Die tägliche Bewegung des Himmels.>
- § 41. Die Bewegung der Sonne am Himmel.
- § 42. Nebeneinflüsse.
Kapitel VI. Die Präzession der Erdachse
- § 43. Geschichtliches.
- § 44. Das Drehmoment der auf die Erde einwirkenden äusseren Kräfte.
- § 45. Bewegungsgleichungen. Permanente und periodische Störungsglieder.
- § 46. Wirkung der einzelnen Bestandteile des Drehmoments.
- § 47. Die Präzession der Erdachse.
- § 48. Periodische Glieder.
Kapitel VII. Die astronomische Nutation der Erdachse
Kapitel VIII. Zeitmessung und Zeitzählung.
Kapitel IX. Das Polwanderungsproblcm und seine mathematische Erfassung
- § 53. Geschichtliches.
- § 54. Geophysikalische Tatsachen.
- § 55. Mathematische Erfassung des vorstehenden Tatsachenmaterials.
Kapitel X. Die dynamische Asymmetrie der Erdrinde und ihre Folgen
Kapitel XI. Der Mechanismus der säkularen Polwanderungen
- § 58. Die vektorielle Grundgleichung der säkularen Bewegung der Erdpole.
- § 59. Periodische Glieder der Polbahnbewegung.
- § 60. Eine andere Ableitung der Grundglelchung der säkularen Bewegung der Erdpole.
- § 61. Allgemeine Eigenschaften des Feldes Ω und der Polbahnkurven.
- § 62. Die Gleichung der ungestörten Polbahnkurve.
- § 63. Die säkulare Bewegung des Poles längs seiner Bahnkurve.
Kapitel XII. Numerische Ausrechnung und kartographische Veranschaulichung der säkularen Polwanderungen
- § 64. Grundlagen der Berechnung.
- § 65. Gang und Ergebnis der Berechnung.
- § 66. Vergleich des durch die vorstehende Berechnung erhaltenen Ergebnisses mit den Dokumenten der Erdgeschichte.
- § 67. Der zeitliche Verlauf der Polverlagerungen.
- § 68. Der Einfluss der Polverlagerungen auf die Orientierung der Erdachse im Weltraume.
- § 69. Nebeneinflüsse.
Kapitel XIII. Der gegenwärtige Bestrahlungszustand der Erde
- § 70. Die Solarkonstante.
- § 71. Das Bestrahlungsgesetz.
- § 72. Die Bestrahlung der Erde in einem gegebenen Zeitpunkte.
- § 73. Der tägliche Bestrahlungsgang.
- § 74. Die täglichen Strahlungsmengen.
- § 75. Die Diskontinuität des Bestrahlungsganges und deren Elimination.
- § 76. Reihenentwicklungen.
- § 77. Der jährliche Gang der Bestrahlung.
- § 78. Die während beliebiger Zeitabschnitte des Jahres zugestrahlten Wärmemengen.
- § 79. Die astronomischen Jahreszeiten.
- § 80. Quantitäten der Bestrahlung während der astronomischen Jahreszeiten.
- § 81. Die den beiden Hemisphären während beliebiger Intervalle des Jahres zugestrahlten Wärmemengen.
Kapitel XIV. Säkulare Änderungen der den Bestrahlungszustand der Erde bestimmenden astronomischen Elemente
- § 82. Mechanismus der säkularen Aenderungen der den Bestrahlungszustand der Erde bestimmenden astronomischen Elemente.
- § 83. Analytische Darstellung der säkularen Aenderungen der Elemente e, Πγ, ε.
- § 84. Numerische Ausrechnungen der säkularen Aenderungen der astronomischen Elemente.
Kapitel XV. Analytische Darstellung des säkularen Ganges der Erdbestrahlung
- § 85. Hilfstabellen zur Berechnung der säkularen Aenderungen der Erdbestrahlung.
- § 86. Allgemeines über den säkularen Gang der Erdbestrahlung.
- § 87. Die kalorischen Jahreszeiten.
- § 88. Die den kalorischen Jahreszeiten der einzelnen Breiten zugehörigen Zeitintervalle.
- § 89. Die während der kalorischen Jahreszeiten den einzelnen Breiten zugestrahlten Wärmemengen.
- § 90. Der kalorische Aequator.
- § 91. Analytische Darstellung des säkularen Bestrahlungsganges der einzelnen Breiten der Erde.
- § 92. Analytische Darstellung des säkularen Bestrahlungsganges einzelner Zonen der Erdoberfläche.
- § 93. Analytische Darstellung des säkularen Ganges der durchschnittlichen Bestrahlung der nördlichen bzw. der südlichen Hemisphäre der Erde.
Kapitel XVI. Das mathematische Klima der Erde. Einleitung. Grundlegende Tatsachen und Gesetze
- § 94.Das mathematische Klima der Erde
- § 95. Die Schichtung der Atmosphäre.
- § 96. Das Bouguer-Lambertsche Gesetz.
- § 97. Numerische Ergebnisse.
- § 98. Die Strahlungsbilanz der Erde.
Kapitel XVII. Zusammenhang zwischen Einstrahlung und Temperatur im Falle eines stationären Bestrahlungszustandes
- § 99. Differentialgleichungen der Strahlungsvorgänge in der Atmosphäre.
- § 100. Integration der vorstehenden Differentialgleichungen für den Fall einer stationären Bestrahlung.
- § 101. Gesetze von Beer, Kirchhoff und Stefan.
- § 102. Das solare Temperaturfeld der Erde.
- § 103. Der Aufbau der Atmosphäre im Strahlungsgleichgewicht.
- § 104. Stabilitätsfragen.
- #167; 105. Einfluss des durchschnittlichen Wasserdampfgehaltes der Atmosphäre auf den thermischen Aufbau derselben.
Kapitel XVIII. Zusammenhang zwischen Einstrahlung und Temperatur im Falle einer variablen Bestrahlung
- § 106. Die Wärmeleitung des Erdbodens.
- § 107. Der Wärmeumsatz des Erdbodens.
- § 108. Integration der Differentialgleichungen des Strahlungsvorganges in der Atmosphäre im Falle variabler Bestrahlung.
- § 109. Vertikale Fortpflanzung der Temperaturoszillationen in der Atmosphäre.
- § 110. Der jährliche Wärmeumsatz der Atmosphäre.
Kapitel XIX. Das Eiszeitenproblem und seine Geschichte
- § 111. Die Eiszeiten.
- § 112. Die alten Theorien der Eiszeiten.
- § 113. Ueber einige weiteren Versuche, die Eiszeiten rechnerisch zu erklären.
Kapitel XX. Verlauf der Erdbestrahlung während der letztverflossenen 600 Jahrtausende
Kapitel XXI. Die Strahlungskurven als Grundlage der Chronologie und der Vollgliederung des Eiszeitalters
- § 116. Die Strahlungskurven und ihre erste Anwendung.
- § 117. Die Zergliederung des alpinen Glazials.
- § 118. Die Vollgliederung des Eiszeitalters.
- § 119. Weitere Anwendungen der Strahlungkurven.
Kapitel XXII. Klimatische Answirkungen des säkularen Ganges der Erdbestrahlung
- § 120. Die unmittelbaren thermischen Effekte des säkularen Ganges der Erdbestrahlung.
- § 121. Die mittelbaren klimatischen Effekte des säkularen Ganges der Erdbestrahlung.
- § 122. Die durch den säkularen Gang der Erdbestrahlung unmittelbar hervorgerufenen Verschiebungen der Schneegrenze.
- § 123. Klimatische Auswirkungen der säkularen Aenderungen des Reflexionsvermögens der Erde.
Kapitel XXIII. Mechanismus und Ablauf der grossen klimatischen Schwankungen des Quartärs
- § 124. Zusammenfassung der Ergebnisse über den säkularen Gang der Erdbestrahlung-und seine klimatischen Auswirkungen.
- § 125. Zeitliche Abfolge und Ausmass der grossen klimatichen Schwankungen der letztverflossenen 660 Jahrtausende.
- § 126. Die vor dem 600. Jahrtausend stattgefundenen klimatischen Schwankungen.
- § 127. Einzelheiten über den Verlauf der klimatischen Schwankungen des Eiszeitalters.
Vorwort
Das vorliegende Werk, das ich durch die hohe Vermittlung der königlich-serbischen Akademie der Öffentlichkeit übergebe, fasst die wichtigsten Ergebnisse meiner dreißigjährigen Arbeit zusammen, ergänzt sie und formt zu einem abgerundeten Ganzen, zu einem besonderen Kapitel der kosmischen Physik. Eine solche systematische Zusammenfassung meiner auf eine ganze Reihe von Problemen sich erstreckenden Untersuchungen war durch den ihnen zu Grunde liegenden Leitgedanken angebahnt und durch deren Ergebnisse ermöglicht, wie dies aus der nachstehenden Schilderung des Werdeganges des vorliegenden Werkes ersichtlich ist.
Es war dies, wie ich es in meinem in nachstehendem Verzeichnis unter 27 angeführten autobiographischen Werke ausführlich erzählte, im Jahre 1911 als mir meine Überlegungen folgendes kundtaten.
Das Newtonsche Gravitationsgesetz, dem die Lehre von der Bewegung der Himmelskörper, die Mechanik des Himmels, ihr festes Fundament verdankt, ist der erste Paragraph im Gesetzbuche des Weltalls und unseres Planetensystems Diesem Paragraphen reiht sich ein zweiter Paragraph an, nicht minder wichtig und nicht weniger umfassend. Der erste Paragraph spricht von der Größe der gegenseitigen Anziehung der Weltkörper, die ihren Lauf regelt und die Planeten zu ihrem Umlauf um die Sonne zwingt, der zweite Paragraph spricht von der Ausbreitung der Strahlung der Gestirne, also auch von der wärmespendenden Kraft der Sonne. Auch diese nimmt, geradeso wie die anziehende Kraft der Sonne, mit dem Quadrat der Entfernung ab; In den Weltraum sich mit Lichtgeschwindigkeit ausbreitend, erreichen die Sonnenstrahlen die Oberflächen der Planeten. Die Wärmemengen, die sie dabei den Planeten zuführen, hängen nicht nur von der Entfernung des betreffenden Planeten von der Sonne ab, sondern auch von dem Einfallswinkel, unter dem die Strahlen den in Betracht gezogenen Teil der Planetenoberfläche erreichen. Die Verteilung der Sonnenwärme auf den Oberflächen der Planeten lässt sich unter Berücksichtigung dieser Tatsachen durch mathematische Formeln erfassen.
Die Bestrahlung der Planeten durch die Sonne, also auch jene des uns am meisten interessierenden unter ihnen, der Erde, ist ununterbrochener Änderung unterworfen. Die Drehung der Erde um ihre Achse hat den Wechsel von Tag und Nacht zur Folge, ihre Umlaufsbewegung um die Sonne ruft den Ablauf der Jahreszeiten hervor; die gegenseitige Anziehung der Planeten ändert langsam aber stetig die Form und die räumliche Lage der Erdbahn; die Präzession der Erdachse bewirkt, dass sich die Äquinoktiallagen der Erde längs dieser veränderlichen Erdbahn verlagern, und dies alles hat den säkularen Gang der Erdbestrahlung zur unausweichlichen Folge.
Alle diese Änderungen lassen sich, dank der Sphärischen Astronomie und der Himmelsmechanik mathematisch exakt beschreiben und in ferne Zeiten Schritt für Schritt verfolgen Der Schlusseffekt der Sonnenstrahlung, der uns ganz besonders interessiert, ist der Temperaturzustand der Planetenoberflächen und der Planetenatmosphären Beim Eintritt der Sonnenstrahlen in die Atmosphärenhülle der Planeten erfährt die Energie, die in diesen Strahlen enthalten ist, mannigfaltige Umwandlungen, um schließlich im jeweiligen Temperaturzustand des Planeten und seiner Atmosphäre ihren sinnfälligen Ausdruck zu finden, ist doch die Sonnenstrahlung die einzige aktive Post im Wärmehaushalt unserer Erde und der mit einer festen Kruste bedeckten Planeten.
Die in den Atmosphärenhüllen der Planeten sich abspielenden Erscheinungen gehorchen ebenfalls wohl begründeten durch mathematische Formeln erfassbaren Gesetzen der Physik. Wenn es also gelingen würde, den Zusammenhang zwischen dem Bestrahlungszustand und dem Temperaturzustand der Planeten zu ermitteln, so wäre es möglich, aus der Stärke der Sonnenstrahlung und aus dem Mechanismus unseres Planetensystems den zeitlichen Ablauf der Temperaturerscheinungen auf den Oberflächen der Planeten mathematisch zu beschreiben und numerisch zu veranschaulichen.
In dieser exakt formulierten Fassung stand dies große kosmische Problem seit jener Zeit im Zielpunkt meiner Forschungen. Die erste Frage, die ich mir vorerst stellen musste, war, ob dieses Problem nicht von jemand anderem schon gelöst worden war. Ich überzeugte mich bald, dass dies nicht der Fall war. Alles, was mit diesem Problem im Zusammenhange stand und was ich aus der ganzen Weltliteratur darüber sammeln konnte, das waren nur einige Abhandlungen, von denen keine einzige dieses Problem in seinem oben angegebenen Umfang erfasste und von denen manche mit kardinalen Fehlern behaftet waren. Während also damals die Lehre von der Bewegung der Himmelskörper, die Mechanik des Himmels, bereits seit hundert Jahren an der ersten Stelle unter den exakten Naturwissenschaften stand, war eine mathematische Lehre von den thermischen Erscheinungen auf den Oberflächen der Planeten nicht einmal ernstlich in Angriff genommen. Ich musste mich also zunächst fragen, was die Ursache dieses Sachverhaltes sei, und fand auf diese Frage die folgende Antwort.
Die Forscher, die sich mit den thermischen Erscheinungen auf der Erdoberfläche, d. h. mit dem Klima der Erde, befassten, die Meteorologen, kümmerten sich damals noch nicht um das Klima der übrigen Planeten. Das Klima der Erde erforschend, waren sie _reine Erfahrungswissenschaftler. Sie hatten keine Veranlassung, sich mit komplizierten mathematischen Theorien zu befassen; die meisten von ihnen wären auch nicht in der Lage, dies zu tun. Man könnte es von ihnen auch gar nicht verlangen, durch den Schornstein den Weg in ein Gebäude zu suchen, dessen Pforte weit geöffnet steht. Warum den Weg über die Sonne unternehmen, um zu erfahren, was auf der Erde geschieht? Hat man nicht auf der Erde Tausende von meteorologischen Stationen errichtet, die uns über alle Einzelheiten der Temperaturerscheinungen zuverlässiger und genauer unterrichten als die vollkommenste Theorie.
Der zweite Grund, warum es niemand vor mir ernstlich unternommen hatte, eine mathematische Theorie des Klimas auf zu bauen, war wohl der, dass man bei einem derartigen Versuch sofort auf eine ganze Reihe komplizierter Probleme stoßen musste, die verschiedenen Gebieten der exakten Wissenschaften angehören, die damals voneinander scharf abgegrenzt waren.
Der dritte, vielleicht der ausschlaggebende Grund, warum sich jene Theorie nicht früher entwickeln konnte, war der Umstand, dass bis zum Jahre 1913 die Stärke der Sonnenstrahlung nicht zuverlässig ermittelt war. Wohl hatten es seit langem viele unternommen, die Intensität der Sonnenstrahlung auszumessen, aber die dabei gewonnenen Messungsergebnisse waren derart verschieden, dass man nicht genau angeben konnte, wieviel Wärme diese Strahlen in der Zeiteinheit der ihnen senkrecht exponierten Flächeneinheit zuführen , d. h. wie groß die Solarkonstante ist. So blieb in der Formel, durch die der zweite Paragraph des Gesetzbuches des Weltalls zum Ausdruck gelangt, eine wichtige Zahl, die Solarkonstante, lange unbekannt. Aus diesem Grunde war damals jede Rechnung, die darauf ausging, aus der Intensität der Sonnenstrahlen die Hauptmerkmale des Erdklimas zu ermitteln, aussichtslos gewesen.
Dies waren die Gründe, warum jenes Problem lange Zeit ungelöst, ja unbemerkt blieb, abseits gelegen an der Dreiländergrenze der Sphärischen Astronomie, der Himmelsmechanik und der Mathematischen Physik. Die Lehrkanzel der Universität in Belgrad, die ich im Jahre 1909 bestiegen hatte, umfasste alle diese wissenschaftlichen Disziplinen, die sonst an den anderen Universitäten voneinander getrennt sind. Diese Koinzidenz, die mir die Inangriffnahme der Behandlung des gestellten Problems ermöglichte, war, so zufällig sie erscheint, doch kein Zufall. Gerade deshalb, weil ich mich mit diesen Disziplinen befasste, war es mir möglich, jenes Problem zu erspähen, zu formulieren und seine Behandlung in Angriff zu nehmen.
Bald war mir folgendes klar geworden. Wenn es tatsächlich gelingen sollte, das gestellte Problem in seinem vollen Umfang zu lösen und dadurch eine mathematische Theorie zu schaffen, mittels der man die Wirkungen der Sonnenstrahlung in Raum und Zeit verfolgen könnte, so wäre man vor allem in der Lage, die wichtigsten Grundzüge des Erdklimas rechnerisch zu ermitteln. Dies allein würde, so möchte es scheinen, nicht Gott weiß was bedeuten, denn man würde bestenfalls nur das gefunden haben, was schon längst bekannt war. Aber ein derartiges Urteil wäre voreilig, denn eine mathematische Theorie des Erdklimas würde uns den ganzen Mechanismus der thermischen Erscheinungen aufdecken , von dem wir bisher nur die Schlusseffekte kannten. Sie würde uns außerdem Auskunft über die Temperaturen der hohen Luftschichten geben, bis zu denen wir noch nicht emporgestiegen sind. Sie würde noch viel weiter vordringen. Dieselbe Wärmequelle, die Sonne, die unsere Erde mit Wärme versorgt, erwärmt auch jene Planeten, die mit festen Krusten bedeckt sind. Die Ergebnisse der neuen Theorie würden auch für diese Planeten und auch für den Erdmond ihre Gültigkeit bewahren. Sie würden uns die ersten zuverlässigen Angaben über das Klima dieser fernen Welten liefern können, von dem wir vorher nichts Bestimmtes wussten. Doch selbst damit wären die Leistungen einer derartigen Theorie nicht erschöpft. Hat sie einmal die Grundzüge des gegenwärtigen Klimas der Erde erfasst, so wäre sie in der Lage, das Klima der Vorzeit zu erforschen und zu beschreiben, wo die Bahnelemente der Erde und die Neigung ihrer Drehachse, wie uns dies die Himmelsmechanik lehrt, andere gewesen sind. Mit einem Worte, die neue Theorie würde uns ermöglichen, die Grenzen unserer direkten Wahrnehmungen weit zu überschreiten.
Diese Betrachtungen bildeten den Leitgedanken meiner daran sich anschließenden langjährigen Arbeit, deren Ergebnisse nach und nach in einer Reihe von Abhandlungen und Werken ihre Veröffentlichung fanden. Ein Verzeichnis dieser Schriften befind et sich am Schlusse des vorliegen Vorwortes. Die in dieses Verzeichnis eingetragenen Schriften sind nach dem Datum ihrer Fertigstellung und nicht nach dem Zeitpunkt ihrer Veröffentlichung geordnet; die durch Sperrschrift gekennzeichneten Werke bilden zusammenfassende Darstellungen der bis zu dem Jahre 1920 bzw. 1930 und 1938 sichergestellten Ergebnisse meiner Arbeit; sie veranschaulichen die wichtigsten Etappen der Erforschung des in der oben angegebenen Richtung beschrittenen neuen Wissensgebietes. Aus diesem stufenförmigen Aufbau ist schließlich das hier zum Abschluss gebrachte Lehrgebäude entstanden.
Zum besseren Verständnis des vorliegenden Werkes erscheint es notwendig, die wichtigsten Phasen seiner Entstehung hier zu überblicken.
In meinem während des Weltkrieges in der Gefangenschaft geschriebenen Werke "Théorie mathématique des phénomènes thermiques produits par La radiation solaire", das auch die Ergebnisse der im Verzeichnis unter 1 bis 6 angeführten Abhandlungen beinhaltet, wurden die wichtigsten Teile des gestellten Problems gelöst, wodurch das begonnene Lehrgebäude seine festen Grundmauern erhielt, auf denen man weiter bauen konnte. Jenes Werk gliedert sich i n zwei Teile, der erste umfasst die Theorie, der zweite deren Anwendungen, die sich auf drei verschiedene Gebiete erstreckten. Das erste derselben umfasste die mathematische Erforschung und Beschreibung des gegenwärtigen Bestrahlungszustandes und des daraus sich ergebenden solaren Klimas der Erde, das zweite die säkularen Variationen der Erdbestrahlung und deren Effekte, das dritte die Erforschung der thermischen Erscheinungen auf den Oberflächen der Planeten.
Die in meinem Erstlingswerke auf dem dritten der drei auf gezählten Anwendungsgebiete durchgeführten Untersuchungen zeichneten sich durch ihre damalige Aktualität aus und schienen eine Zeit lang das wichtigste Ergebnis meines Buches zu sein, weil im Augenblicke seiner Veröffentlichung die Frage nach der Bewohnbarkeit der Planeten und namentlich jener des Planeten Mars im Blickpunkte der astronomischen Forschung stand. Die in meinem Werke geschaffene Theorie ermöglichte mir tatsächlich, nicht nur jene Wärmemengen zuverlässig zu berechnen, die im Laufe eines Marsjahres den verschiedenen Breiten seiner Oberfläche zu gestrahlt werden, sondern auch die zugehörigen jährlichen Temperaturen dieser Breiten zu ermitteln. Aus diesem Resultate ergab sich eine mittlere Temperatur der untersten Luftschlicht des Planeten von -17 °Celsius. Durch dieses Ergebnis, das bald die Aufmerksamkeit der Astronomen auf sich lenkte, wurde die damals weitverbreitete Ansicht von der Bewohnbarkeit dieses Planeten durch höher organisierte Lebewesen endgültig zerstört. Auch die von den amerikanischen Astronomen fünf Jahre nach der Veröffentlichung meines Werkes durchgeführten Messungen der von der Marsoberfläche zu uns gelangenden Strahlung bestätigten die Ergebnisse meiner Berechnungen vollauf.
In meiner "Théorie mathématique" wurden auch die Temperaturverhältnisse auf der Oberfläche des Merkurs und jener des Erdmondes einer mathematischen Untersuchung unterworfen, die durch den Umstand begünstigt, dass diese beiden Himmelskörper keine atmosphärische Hülle besitzen, zu numerischen Ergebnissen führte. Was den Planeten Venus anbelangt, konnte in Unkenntnis seiner Rotationsdauer und der Lage seiner Drehachse nur die obere Grenze der Mitteltemperatur seiner untersten Atmosphärenschicht festgelegt werden, die ein organisches Leben auf diesem Planeten nicht ausschließt.
Diese Ergebnisse meiner "Théorie mathématique", die in dem ausführlichen Bericht Schoenberg's "Über die Temperaturen der Planeten. Physikalische Zeitschrift>. 26. Jahrgang, 1925" ihre Würdigung fanden und jene der beiden im nachstehenden Verzeichnis unter 12 und 16 an geführten Abhandlungen, die sich mit dem thermischen Aufbau der Planeten Jupiter, Saturn, Uranus und Neptun und jenem der Uratmosphäre der Erde befassen, habe ich, wie dies in seinem Titel angedeutet, nicht in den Rahmen des vorliegenden Werkes einbeziehen können, weil dadurch dessen Umfang ein viel zu großer geworden wäre, denn bald nach der Veröffentlichung meines Erstlingswerkes erweiterte sich das Anwendungsgebiet der darin niedergelegten Theorie ganz gewaltig, was einen·weiteren Ausbau derselben nach sich zog. Dazu kam es auf folgende Weise.
Die Ergebnisse meiner "Théorie mathématique" lenkten auf sich die Aufmerksamkeit des großen deutschen Klimatologen Wladimir Köppen, der die Tragweite dieser Theorie richtig erkannte. Er arbeitete damals mit seinem Schwiegersohne Alfred Wegener an dem Werke "Die Klimate der geologischen Vorzeit" und gedachte darin meine Theorie zu verwerten. Nach kurzem Briefwechsel luden mich beide Forscher zur Mitarbeit an ihrem Werke ein. Diese Einladung freudig annehmend, überdachte ich, bevor ich an die Ausarbeitung des für ihr Werk bestimmten Beitrages schritt, ob es nicht möglich wäre, die in der "Théorie mathématique" mitgeteilte Methode der Darstellung des säkularen Ganges der Erdbestrahlung zu vervollkommnen. Die gelang mir durch die in meiner im nachstehenden Verzeichnis unter 8 angeführten Abhandlung mitgeteilten Überlegungen, aus denen durch die Einführung der kalorischen Jahreszeiten eine einwandfreie Methode zur Darstellung des säkularen Bestrahlungsganges hervorging, die ich mit jeder weiteren Veröffentlichung über diesen Gegenstand verfeinerte, um ihr schließlich ihre im Kapitel XV dieses Werkes bis in alle Einzelheiten ausgearbeitete endgültige Form zu geben.
Diese Methode wandte ich an, um auf Wunsch von Köppen die säkularen Änderungen zu berechnen, die die sommerliche Bestrahlung der geographischen Breiten von 55° bzw. 60° und 65° nördlich während der letztverflossenen 650 Jahrtausende erfahren hat. Dabei beschränkte ich mich darauf, nur die Amplituden dieser Veränderungen zu berechnen, stellte das Ergebnis der Rechnung durch Zackenlinien dar und schickte dieses Graphikon mit den erforderlichen Erläuterungen anfangs des Jahres 1923 an Köppen, der diesen Beitrag seinem und Wegeners Werke einverleibte. Ich aber musste mich unverzüglich an deren wissenschaftlichen Problem zuwenden. Im Mai 1923 tagte in Konstantinopel der Kongress der orthodoxen orientalischen Kirchen, der sich mit der Reform des julianischen Kalenders, der damals bei diesen Kirchen im Gebrauch stand, befassen sollte. Ich hatte die Ehre als bevollmächtigter Delegierte der serbischen orthodoxen Kirche und der königlichen Regierung an diesem Kongress teil zu nehmen und die Genugtuung, mein auf die Kalenderreform sich beziehenden Vorschläge von diesem Kongress angenommen zu sehen, wodurch der neue Kalender der orientalischen Kirchen geschaffen wurde, worüber ich in den im nachstehenden Verzeichnis unter 9 und 10 eingetragenen Schriften berichtete und worüber im Kapitel VIII dieses Werkes ebenfalls die Rede sein wird. Im Jahre 1924 wurde das Köppen-Wegenersche Werk "Die Klimate der geologischen Vorzeit" veröffentlicht. Eines der wichtigsten Ergebnisse desselben war, dass in meinem Strahlungsdiagramm den Ablauf des Eiszeitalters erkannte, wodurch die auf zuverlässiger astronomischer Grundlage beruhende Chronologie dieses Zeitalters geschaffen wurde, wie ich dies in meiner im nachstehenden Verzeichnis unter 11 angeführten akademischen Antrittsrede wie folgt berichten konnte.
Unser bürgerliche und kirchliche Kalender ist seinem Wesen nach nichts anderes als eine Abzählung der Himmelserscheinungen. In seinen Elementen, dem Tag, dem Monat und dem Jahr, spieg eln sich die kosmischen Erscheinungen, die Drehung der Erde, der Umlauf des Mondes und die Umkreisung der Sonne durch die Erde, wider. Geradeso verhält es sich mit dem durch die Strahlungskurven geschaffenen Kalender des Eiszeitalters. In ihm spiegeln sich die kosmischen Erscheinungen höherer Kategorie wider, die oszillierenden Schwankungen der Ekliptik-Schiefe und der Exzentrizität der Erdbahn und der Umlauf des Perihels. Die Ungleichheit und die Unregelmäßigkeit dieser Erscheinungen ist es, die die äußerst komplizierten, aber rechnerisch zuverlässig Schritt für Schritt verfolgbaren Schwankungen der Erdbestrahlung verursachen, die ihrerseits derartig tiefe Spuren im Antlitz der Erde hinterlassen hatten, dass man in der Lage ist, diese Spuren astronomisch zu datieren.
Durch das Köppen-Wegenersche Werk haben meine Strahlungskurven eine große Publizität erlangt und sind, wie dies im Kapitel XXI berichtet werden wird, zum Ausgangspunkt an derer grundlegender Arbeiten der Klimatologen und Geologen geworden. Als bald darnach W. Köppen in Verein mit R. Geiger an die Ausgabe seines groß angelegten fünfbändigen Handbuches der Klimatologie schritt, übertrug er mir die Ausarbeitung des Einleitungsartikels (Band 1, Teil A) dieses Handbuches, der den Titel "Mathematische Klimalehre und Astronomische Theorie der Klimaschwankungen" erhielt und 1930 veröffentlicht wurde. Dieses Buch, in dem auch die Ergebnisse meiner inzwischen erschienenen, im nachstehenden Verzeichnis unter 13 und 14 angeführten Abhandlungen berücksichtigt wurden, bildet die zweite zusammenfassende Darstellung meiner bis zu jenem Zeitpunkt auf diesem Gebiete vollführten Forschungen. In demselben bildet nur der Planet Erde mit seinem gegenwärtigen und vorzeitlichen Klima den Gegenstand der Behandlung, wodurch die Richtung angedeutet erscheint, in der sich das neue Wissensgebiet weiter entwickeln sollte. In dieser Richtung weist das Buch einen wesentlichen Fortschritt gegenüber der "Théorie mathématique" auf, weil darin die mathematische Theorie des gegenwärtigen Erdklimas, die mathematische Klimalehre, durch die vollständige Lösung ihrer Grundprobleme zu einem abgeschlossenen Lehrgebiet der exakten Wissenschaften geworden ist. Auch die astronomische Theorie der Klimaschwankungen erhielt in diesem Buche ihre festen Umrisse und führte zur numerischen Berechnung dieser Schwankungen. Die in diesem Buche enthaltene vielzahlige Tabelle stellt eine ausführliche, in mathematischer Sprache verfasste Geschichte der Erdbestrahlung der letztverflossenen 600 Jahrtausende dar.
Noch während der Niederschrift der "Mathematischen Klimalehre" erweiterte sich mein Arbeitsgebiet durch neue Probleme, die mit den in jenem Buche behandelten in enger Beziehung standen. Ende des Jahres 1927 erhielt ich von B. Gutenberg die Einladung zur Mitarbeit an seinem auf zehn Bände vorgesehenem "Handbuch der Geophysik". Ich war selbstverständlich gern bereit, dieser ehrenden Aufforderung zu entsprechen, war jedoch wegen der bereits übernommenen Verpflichtungen nicht in der Lage, auf die von Gutenberg vorgesehenen Termine für die Ablieferung der mir zugedachten Beiträge einzugehen. Gutenberg kam mir aber weitgehend entgegen. Er erklärte sich bereit, die Einordnung des Materiales in die einzelnen Bände des Handbuches und die Termine ihrer Veröffentlichung derart umzuändern, dass meine Mitarbeit ermöglicht werde und nahm alle meine diesbezüglichen Vorschläge verständnisvoll an. Einer dieser Vorschläge ging dahin, dem ersten Band den Titel zu geben "Die Erde als Planet" und darin jene Fragen zu behandeln, die diesen höheren Standpunkt der Geophysik zum Ausdruck bringen. Ich übernahm es für diesen Band drei von einander getrennte Abschnitte zu liefern: "Stellung und Bewegung der Erde im Weltall", "Drehbewegungen der Erde" und "Säkulare Polverlagerungen". Die Fertigstellung der zwei ersten Abschnitte bereitete mir keine Schwierigkeiten, betreffen sie doch klassische Probleme der Himmelsmechanik, die ich mit dem modernen Werkzeug der Vektoranalysis bearbeitend bald nach der Veröffentlichung meiner "Mathematischen Klimalehre" fertigstellte und dem Herausgeber des Handbuches einlieferte, der sie unverzüglich dem Drucke übergab. Anders war es mit den "Säkularen Polverlagerungen". In dieser geophysisch sehr wichtigen Fragestanden damals die Lehren der beschreibenden Naturwissenschaften und jene der exakten Wissenschaften in schroffem Gegensatze, Während die beschreibenden Wissenschaften untrügliche Belege dafür besaßen, dass während der Vorzeit die Lage der Pole auf der Erdoberfläche eine andere gewesen war als heute, stand die exakte Wissenschaft dieser Erscheinung ratlos gegenüber. Der Begriff der Pole ist ein solcher der Mechanik, die Pole veranschaulichen die Durchstoßpunkte der Drehachse der Erde mit deren Oberfläche. Die Drehbewegung der Erde muss den Gesetzen der Mechanik gehorchen. Diese Wissenschaft war, wie es aus meinem vorangehen den Artikel folgte, tatsächlich in der Lage, alle bisher astronomisch festgestellten Eigentümlichkeiten dieser Drehbewegung, die Präzession, die astronomische und die freie Nutation der Erdachse auf das befriedigendste zu erklären und zu beschreiben, aber ihre Lehren waren nicht imstande, eine Ursache für größere Verlagerungen der Drehpole der Erde anzugeben und deren Mechanismus zu erklären. Ich unternahm also mit meinem Artikel, diese ganze Frage noch einmal zu überprüfen und zu klären. Es ergab sich dabei, dass die Ursache, warum alle früheren Versuche fruchtlos geblieben sind, darin zu erblicken ist, dass man bei jenen theoretischen Untersuchungen der Drehbewegungen der Erde nicht alle Eigentümlichkeiten des Erdkörpers in Rechnung gestellt hatte. Der Bau der Erde ist viel komplizierter als es früher die Theoretiker bei ihren Untersuchungen vorausgesetzt halten. Es hat sich auch hier abermals gezeigt, dass die gegenwärtige Trennung der Wissenschaften in ihre Spezialgebiete für manches neue Problem nachteilig ist und man bei Stellung eines solchen Problems gezwungen ist, vorerst einen Brückenschlag zwischen zwei solchen Gebieten zu bewerkstelligen. Ich musste also, bevor ich mich an die Lösung des gestellten Problems wagen konnte, als Himmelsmechaniker in die Schule der Geophysiker mich begeben Hier war mein Lehrer A1fred Wegener. Das Studium seiner wissenschaftlichen Arbeiten und die mehrfachen Unterredungen, die ich mit ihm gepflogen hatte, haben mich mit geophysikalischen Tatsachen vertraut gemacht, die sonst einem Mathematiker und Himmelsmechaniker wenig geläufig sind. Diese Gespräche haben mir nicht nur die grundlegende Bedeutung des Polverlagerungsproblems offenbart, sondern mich zu neuen Anschauungen über die Beschaffenheit des Erdkörpers geführt, die sich in der Folge als fruchtbringend erweisen sollten. Erst als ich mich mit dem Aufbau der Erdkruste und namentlich mit der isostatischen Lagerung der Kontinentalschollen auf ihrer gegen langandauernde Kräfte nachgiebigen Unterlage vertraut machte, konnte ich das Problem fest anpacken und beweisen, dass die durch die im Tauchgleichgewicht gebetteten und aus ihrer Unterlage hervor ragenden Kontinentaltafeln verursachte dynamische Asymmetrie des Erdkörpers eine langsam vor sich gehende, aber unaufhaltsame Verschiebung der Sialdecke der Erde auf ihrer nachgiebigen Unterlage, also eine säkulare Verlagerung der Erdpole zur Folge haben muss. Die weitere Untersuchung ergab, dass diese Verlagerung der Pole längs der orthogonalen Trajektorie des Trägheitsfeldes dieser Sialdecke vor sich gehen muss. Dadurch wurde das grundlegende Theorem hinsichtlich der Polverlagerung gewonnen , das man in der Literatur mit meinem Namen bezeichnete und aus dem sich alle weiteren Einzelheiten dieser Erscheinung ableiten und mathematisch darstellen ließen.
Durch die Ableitung dieses Theorems, das in meiner im nachstehenden Verzeichnis unter 19 angeführten Abhandlung seine erste Veröffentlichung fand, wurde das mir vom Herausgeber des "Handbuches der Geophysik" zur Behandlung zugewiesene Problem im Prinzip gelöst. Zur weiteren Behandlung dieses Problems blieb aber keine Zeit mehr übrig, weil der Herausgeber die sofortige Drucklegung meines bis zu diesem Stadium gediehenen Beitrages wünschte. Wir vereinbarten also, dass die weitere Behandlung der Polverlagerungsfrage in meinem für den neunten Band des Handbuches vorgesehenem Beitrage "Astronomische Mittel zur Erforschung der erdgeschichtlichen Klimate" durchgeführt werden möge und so geschah es. Die Drucklegung dieses letzten Beitrages verzögerte sich durch den inzwischen heran gebrochenen wirtschaftlichen Niedergang beträchtlich und erfolgte erst im Juli 1938. Ich hatte aber keine Ursache, mich über diese Verzögerung zu beklagen, denn dadurch habe ich Zeit gewonnen, mehrere wichtige Fragen meines Forschungsgebietes zu kläre n und zu lösen. Die geschah in einer Reihe von Abhandlungen, die in den Jahren 1932 bis 1937 veröffentlicht wurden und die im nachstehenden Verzeichnis unter 21, 22, 23, 24, 25 und 28 angeführt sind.
Die fünf ersten dieser Abhandlungen betrafen das Polverlagerungsproblem. In denselben wurde die Differentialgleichung der Polverlagerung integriert, d. h. die analytische Gleichung der Polbahnkurve abgeleitet. Mit Hilfe dieser Gleichung konnte dann an die numerische Berechnung der aus der Konfiguration der Kontinente sich ergebenden säkularen Bahnen der beiden Erdpole geschritten und das Ergebnis der Rechnung mit den Dokumenten der Erdgeschichte verglichen und beglaubigt werden. Auch eine neue von den Polfluchtkräften ausgehende Ableitung der Grundgleichung der säkularen Polverlagerungen konnte als ein weiterer Beleg für die Richtigkeit dieser Gleichung geliefert werden.
Nicht minder wichtig waren die Ergebnisse meiner Forschungen über die Auswirkungen des säkularen Ganges der Erdbestrahlung, die ich in meiner im nachstehenden Verzeichnis unter 28 angeführten Abhandlung veröffentlichte. Das wichtigste derselben betraf die Frage, ob der durch die Veränderlichkeit der astronomischen Elemente hervorgerufene Bestrahlungsgang der Erde, an dessen durch die Rechnung sich ergebenden Rhythmus nicht mehr zu zweifeln war, ausreichend sei, um auch die größten klimatischen Schwankungen des Quartärs in ihrem vollem Umfang zu erklären. Manche Gelehrte bezweifelten dies, und es war deshalb wünschenswert, meine Berechnungen des säkularen Ganges der Erdbestrahlung durch die Ermittlung der klimatischen Effekte dieses Ganges zu vervollständigen, um zu sehen, wie groß diese Effekte gewesen sind. Einen Schritt in dieser Richtung habe ich bereits in meiner "Mathematischen Klimalehre" gemacht, aber den entscheidenden erst in den "Neuen Ergebnissen der astronomischen Theorie der Klimaschwankungen" vollführt. Da bei ging ich von der mathematischen Analyse des Zusammenhanges zwischen der Höhenlage der Schneegrenze und der zugehörigen dem kalorischen Sommerhalbjahr entsprechenden Strahlungsmenge aus, und fand, dass jeder Veränderung dieser Menge von einer kanonischen Einheit eine Verschiebung der Schneegrenze von einem Meter entspricht. Ich fand nachträglich, dass dasselbe Resultat auch aus dem in der "Mathematischen Klimalehre" abgeleiteten Zusammenhang zwischen Bestrahlung und Temperatur zwangläufig folgt.
Auf Grund dieses Ergebnisses konnte der wichtigste klimatische Effekt des vorzeitlichen Ablaufes der Erdbestrahlung, die dadurch hervorgerufenen Verschiebungen der Schneegrenze, erfasst werden: man hatte die in meinen Tabellen mitgeteilten Zahlen, die die Änderungen der sommerlichen Bestrahlung der einzelnen geographischen Breiten in kanonischen Einheiten wiedergeben, einfach als Meter zu deuten, um die zugehörigen Verschiebungen der Schneegrenze zu erhalten. Da bei bedeutet das Vorzeichen + die Verschiebung der Schneegrenze nach oben, das Zeichen - die Verschiebung nach unten. Dadurch haben jene Tabellen einen mit der Hand erfassbaren klimatologischen Inhalt erhalten.
Die derart gedeuteten Tabellen der Erdbestrahlung zeigen, dass die durch die Änderungen dieser Bestrahlung an Ort und Stelle hervorgerufenen Verschiebungen der Schneegrenze genügend mächtig gewesen sind, um deutliche Spuren zu hinterlassen, also den säkularen Bestrahlungsgang der Erde auf ihrem Antlitz zu markieren, aber nicht ausreichend waren, um die großen Vereisungen der Vorzeit in ihrem vollem Umfang hervorzurufen. Zu diesem vollem Ausmaß der Vereisungen war ein weiterer klimatischer Faktor erforderlich. Um diesen Faktor zu entdecken und mathematisch zu erfassen, musste noch ein letzter, dem Ziele führende Schritt gemacht werden, zu dem mich folgende Überlegungen führten.
Sind wir imstande, rechnerisch zu verfolgen, wie sich die Schneegrenze im Laufe der Vorzeit nach oben bzw. nach unten verschoben hatte, so sind wir dadurch in die Lage versetzt, auch jene Änderungen rechnerisch zu verfolgen, die die polaren Eiskalotten während der Vorzeit Erfahren hatten. Diese schneeweißen Polarkappen besitzen ein sehr hohes Reflexionsvermögen, weshalb sie einen namhaften Teil der ihnen zu gestrahlten Wärmemengen in den Weltraum zu rückweisen, der dadurch für den Wärmehaushalt der Erde verloren geht. Vergrößert sich also durch die säkulare Verschiebung der Schneegrenze nach unten die mit Eis und Schnee bedeckte Kalotte der in Betracht gezogenen Hemisphäre der Erde, so wird durch das vergrößerte Reflexionsvermögen dieser Hemisphäre ihre nutzbare Bestrahlung vermindert, und daraus resultiert eine weitere, sekundäre Verschiebung der Schneegrenze nach unten.
Es handelte sich also darum, auch dies durch das veränderte Reflexionsvermögen hervorgerufene Verschiebung der Schneegrenze mit ihrer primären Ursache, dem Gang der Erdbestrahlung, in Beziehung zu bringen und mathematisch zu erfassen. Ich bemühte mich bereits in meiner "Mathematischen Klimalehre" diesbezügliche Berechnungen durchzuführen, stieß aber dabei auf Schwierigkeiten, die davon herrührten, dass ich keine verlässliche numerische Angabe darüber besaß, welcher Bruchteil der Wärmestrahlung der Sonne von der mit Schnee bzw. mit Eis bedeckten Flächeneinheit in den Weltraum zurückreflektiert wird. Eine erfolgversprechende Berechnung wäre ohne eine diesbezügliche Angabe nicht möglich gewesen, und eine solche konnte nur durch systematische Forschungen in schneebedeckten Gebieten der Erde gewonnen werden, was aber damals noch nicht geschehen ist. Ich musste also mein im Sinne gehabtes Vorhaben aufgeben bis derartige Messungen durchgeführt wären.
Ich habe, und hier hatte ich, so wie es auch mit der Ermittlung der Solarkonstante der Fall gewesen ist, wieder Glück - nicht lange warten müssen lm Sommer des Jahres 1933 erhielt ich aus Paris eine wissenschaftliche Arbeit des Herrn Joseph Devaux, in der dieser junge Gelehrte, der bald nach her bei einer Forschungsreise in die polaren Gegenden seinen Tod fand, die Ergebnisse seiner auf den Gletschern der Pyrenäen und den Alpen und in Grönland durchgeführten Untersuchungen über das Reflexionsvermögen dieser Schneebedeckungen bekannt gab. In dieser Abhandlung fand ich die für die Durchführung meiner Berechnungen erforderliche zuverlässig ermittelte numerische Angabe. Ich konnte also meine Berechnungen auf einer gesicherten Basis durchführen.
Die Berechnungen, die ich nach Veröffentlichung meines im nachstehenden Verzeichnis unter 26 angeführten Lehrbuches der Mechanik des Himmels durchführte und in meinen "Neuen Ergebnissen" veröffentlichte, ergaben, dass der mit Berücksichtigung des veränderlichen Reflexionsvermögens der Erde berechnete vorzeitliche Gang der Erdbestrahlung vollkommen ausreicht, um auch die größten klimatischen Änderungen des Quartärs in ihrem volle m Umfang zu erklären. Die abkühlende Wirkung der zeitweilig verbreiterten Eiskalotten der Erde gesellte sich als sekundärer Effekt dem säkularen Gange der Erdbestrahlung hinzu, denn sie war durch diesen Gang hervorgerufen. Deshalb weisen die neuen, mit Berücksichtigung dieses Effektes ermittelten Strahlungskurven den selben Rhythmus wie die früher berechneten auf, und zeichnen sich nur durch ihre größeren Ausschläge aus. Aus diesem Grunde hat mein Kalender des Eiszeitalters auch weiterhin seine Gültigkeit behalten, nur sind darin die großen Ereignisse der Vorzeit, ähnlich den Feiertagen des bürgerlichen Kalenders, mit fetten Buchstaben eingetragen.
Als ich die endgültige Niederschrift meines letzten Beitrages für das "Handbuch der Geophysik" der "Astronomischen Mitteln zur Erforschung der erdgeschichtlichen Klimate", in Angriff nahm, waren alle noch offengebliebenen Fragen vollständig gelöst. So konnte ich diese Veröffentlichung als den Schlussstein meiner Forschungen auf dem Gebiete der Erdgeschichte betrachten und in meinen zwei Vorträgen, die ich Ende des Jahres 1937 an den Universitäten in Prag und Brünn hielt und die im nachstehenden Verzeichnis unter 30 angeführt sind, erklären, dass ich damit meine Arbeit auf diesem Gebiete· als abgeschlossen betrachte. Bald nachher sah ich aber ein, dass mein Lebenswerk damit nicht vollendet war und ich ihm noch weitere Arbeitsjahre widmen müsse.
Die Mechanik des Himmels war eine der beiden Grundmauern, auf denen das vor mir vor vielen Jahren begonnene Lehrgebäude errichtet stand. Ihre Lehren für den Aufbau dieses Gebäudes benützend, habe ich gesehen, dass nur ein besonderer Teil derselben für Probleme, mit denen ich mich befasste, in Betracht kommt, wie sich dies aus verschiedenen Zielen der Astronomie und jenen der Geophysik naturgemäß ergibt. Für den Astronomen ist unsere Erde der Standort, von dem aus er die Himmelserscheinungen erforscht, und das Bezugssystem, auf das er die mathematische Beschreibung dieser Erscheinungen bezieht; für den Geophysiker bildet die Erde das einzige Objekt seiner Untersuchungen. Für den Astronomen sind alle Himmelserscheinungen von Interesse, für den Geophysiker nur jene, die den Lebenslauf der Erde und ihrer Welt beeinflussen. Bei meinen Untersuchungen ward mir die Aufgabe zu teil, die die Geschicke der Erde betreffenden Lehren der Himmelsmechanik aus dem umfangreichen System dieser Wissenschaft herauszuschälen, um sie bei meinen Forschungen zu benützen. Bei dieser Auslese habe ich die Beobachtung gemacht, dass manche von diesen Lehren in den Werken über Himmelsmechanik stiefmütterlich behandelt erscheint und dem ausübenden Astronomen nicht genügend geläufig ist. Den auf dem Gebiete der beschreibenden Wissenschaften tätigen Forschern blieben diese Lehren größtenteils unzugänglich. Darüber belehrten mich die Einwände, die man seitens einiger dieser Forscher gegen meine Theorie erhoben hat. Alle ihre Einwände rührten, wie man im sechsten Abschnitt deutlich sehen wird und wie es sich aus meinem im nachstehenden Verzeichnis unter 32 angeführten und im § 113 wiedergebenden Referat ebenfalls ergeben hat, davor her, dass keiner der erwähnten Forscher genügende Kenntnisse der exakten Wissenschaft besaß, um eine astronomische Theorie begutachten zu können· Dies alles überzeugte mich, dass meine Theorie erst dann ein in sich abgeschlossenes und auch den beschreibenden Wissenschaften zugängliches Lehrgebiet bilden wird, wenn ich sie durch die für die Geophysik in Betracht kommenden Lehren der Himmelsmechanik ergänze. Einen ersten Schritt in dieser Richtung habe ich bereits in meinen drei im nachstehend en Verzeichnis unter 17, 18 und 20 angeführten Artikeln des "Handbuches der Geophysik" getan, um die damit begonnene Arbeit erst durch das vorliegende Werk zu vollenden. Darüber möchte ich folgendes vorausschicken.
Die für meine Theorie wichtigen Lehren der Himmelsmechanik betreffen die säkularen Störungen der Planeten und die Drehbewegungen der Erde. Bei der Neubearbeitung der Theorie der säkularen Störungen, die ich in meiner im nachstehenden Verzeichnis unter 31 angeführten Abhandlung einleitete und hier zu Ende führte, bin ich durch Einführung vektorieller Elemente eigene Wege gegangen und habe derselben eine für ihre Anwendungen zweckmäßigere Form gegeben, ohne dadurch die Endergebnisse der klassischen Theorie zu ändern. Die Theorie der Drehbewegungen der Erde, die ich hier in der ihr von mir in dem gleichbetitelten Handbuchartikel gegebenen Form wiedergebe, habe ich durch die Ergebnisse meiner Untersuchungen über die säkularen Wanderungen der Pole wesentlich erweitern können.
Mit dem allgemeinen Problem der Drehbewegung der Himmelskörper haben sich auch meine beiden Kollegen, Professoren der Belgrader Universität A. Bilimovitch und W. Jardetzky, erfolgreich befasst. W. Jardetzky hat sich dabei mit dem zonalen Drehbewegungszustand der Himmelskörper, den auch unsere Erde einst durchgemacht hat und der möglicherweise noch nicht ganz ausgeklungen ist, sehr eingehend beschäftigt. Seine diesbezüglichen Untersuchungen hat er in seinem Werke "Recherches mathematiques sur l'evolution de la Terre", das ebenfalls als Veröffentlichung der königlich serbischen Akademie erschienen ist, zusammengefasst und dadurch die auf ein Jahrzehnt auf diesem Gebiet der Himmelsmechanik sich erstreckende Arbeit unserer Belgrader Schule zu eine m schönen Abschluss gebracht. Als ich die für das Verständnis meiner Theorie erforderlichen Lehren der Himmelsmechanik vervollständigte und in der hierzu entsprechenden Form zu einem Ganzen zusammenfügte, führte mich eine Um schau über das bis dahin geleistete zu neuen Entschlüssen, die durch folgende Überlegungen veranlasst wurden.
Im Frühjahr 1938 war meine Abhandlung "Neue Ergebnisse der astronomischen Theorie der Klimaschwankungen" erschienen und ich hatte noch nicht Zeit gefunden, Sonderabdrücke dieser Abhandlung an meine engere Fachgenossen zu versenden, setzte, wohl durch eine in der Meteorologischen Zeitschrift erschienene und von W. Wundt herrührende Besprechung derselben ausgelöst, eine rege Nachfrage nach dieser Arbeit ein. In rascher Folge erhielt ich Briefe auch aus außereuropäischen Ländern, aus Nord- und Südamerika, aus Südafrika und aus Asien, in denen ich um die Übersendung dieser Abhandlung ersucht wurde. Mit 50 Exemplaren, die ich hatte, konnte ich nicht alle diese Wünsche befriedigen. Dies überzeugte mich, dass das Interesse an meiner Theorie rege geblieben ist. Dies bewies mir auch der Umstand, dass im Laufe desselben Jahres meine "Mathematische Klimalehre" ins russische übersetzt und 1939 in 4000 Exemplaren gedruckt worden ist. Ich dachte also darüber nach, wie ich den durch die vorstehenden Begebenheiten mir zur Kenntnis gebrachten Wünschen am besten nachkommen könnte. Meine beiden die Theorie der erdgeschichtlichen Klimate ausführlich behandelnden Schriften ergänzen sich gegenseitig. Der räumliche Umfang meiner "Astronomischer Mittel" wurde schon im Jahre 1927, lange Zeit vor Inangriffnahme dieser Arbeit, festgelegt. Damals ahnte ich nicht, dass sich dieser Rahmen durch die inzwischen erfolgte Lösung neuer Probleme als zu eng erweisen sollte. Aus diesem Grunde und obwohl mir der Herausgeber in entgegen kommender Art ausnahmsweise erlaubt hat, den vorgesehenen Umfang meines Beitrages zu überschreiten, bildet diese Veröffentlichung keine zusammenfassende Darstellung meiner Forschungsergebnisse, sondern nur eine Ergänzung meiner "Mathematischen Klimalehre". Es ist aber zu berücksichtigen, dass diese beiden Veröffentlichungen, von denen die erste einen Bestandteil des fünfbändigen "Handbuches der Klimatologie", und die zweite einen solchen des zehnbändigen "Handbuches der Geophysik" bildet, einzelnen Forschern schwer zugänglich sind, weil selbst nur wenige der wissenschaftlichen Anstalten diese beiden viel bändigen Sammelwerke besitzen. Alle diese Erwägungen führten mich zum Entschluss, an eine vollständige zusammenfassende Darstellung meines Lebenswerkes zu schreiten.
Dies ist der Werdegang meines neuen Werkes, in dem alle wichtigsten Ergebnisse meiner Forschungen über das Klima der Gegenwart und der Vorzeit mit ihren himmelsmechanischen Grundlagen vereinigt, erweitert und vervollständigt erscheinen und ein zusammenhängendes Ganze bilden, zu dessen vollem Verständnis nur die Kenntnisse der höheren Mathematik und der Vektoranalysis erforderlich sind. Die ersten drei Abschnitte des Werkes sind jenen Grundlagen, also den aus dem Newtonschen Gravitationsgesetz sich ergebenden Konsequenzen und den für meine Theorie ebenfalls wichtigen Lehren der Sphärischen Astronomie gewidmet, die übrigen drei Abschnitte betreffen die aus dem Bestrahlungsgesetz sich ergeben den Schlussfolgerungen. In dieser Zweiteilung gelangt der Leitgedanke aller meiner Forschungen zum sinnfälligen Ausdruck.
Aus diesem Werdegang meines Werkes und aus seinem soeben gekennzeichneten Inhalt ergibt sich auch die Sonderstellung, die das Werk im System der Wissenschaften einnimmt. Die Hauptergebnisse des Werkes sind, wie es seine programmatische Grundidee forderte, ohne Zuhilfenahme irgend welcher Hypothesen aus dem Newtonschen Gravitationsgesetz und aus dem Bestrahlungsgesetz gewonnen worden. Wo es notwendig war, sich auch anderer Doktrinen der Naturwissenschaft zu bedienen, so waren es nur wohl begründete Gesetze der Physik oder anerkannte Lehren der Geophysik. Deshalb gehört das Werk ganz und gar dem Gebiet der exakten Wissenschaften an.
Bei der Berechnung des säkularen Ganges der Erdbestrahlung, der im vorliegenden Werke durch die umfangreiche Tabelle XXV zur vollständigen numerischen Darstellung gebracht wurde, habe ich nur von dem Newtonschen Gravitationsgesetz und von dem Bestrahlungsgesetz Gebrauch machen müssen. Diese beiden Gesetze gehören zu den exaktesten Gesetzen unserer heutigen Naturwissenschaft, weshalb der Berechnung jener Tabelle der Charakter ein es astronomischen Kalküls zukommt. Mit denselben Hilfsmitteln, mit denen man die Zeitpunkte der während der Vorzeit stattgefundenen Sonnen- und Mondfinsternisse zu berechnen pflegt, erscheinen hier die Epochen der einzelnen Phasen des säkularen Ganges der Erdbestrahlung ermittelt. Weil man das Ergebnis der Berechnung der stattgefundenen Finsternisse als Kanon der Finsternisse zu bezeichnen gewöhnt ist, kann man das Ergebnis meiner Berechnungen als Kanon der Erdbestrahlung bezeichnen. Dies rechtfertigt den Haupttitel, den ich meinem Werke gegeben habe. Die ersten zwanzig Kapitel dieses Werkes geben diesen Kanon mit allen seinen theoretischen Grundlagen wieder.
Die letzten drei Kapitel des Werkes sind den Anwendungen dieses Kanons auf das Eiszeitenproblem gewidmet, wie dies im Untertitel des Werkes angegeben ist. Die Anwendungen, die meine Strahlungskurven seitens der Klimatologen und der Geologen erfahren haben, sind zahlreich: ich habe in meinem Buche über hundert diesbezügliche Abhandlungen und Werke anführen und benützen können, in denen man sich über 600 Mal auf mich und noch ausgiebiger auf meine Strahlungskurven beruft. Durch diese Anwendungen greift das auf dem Boden der exakten Wissenschaft fußende Werk auf das Gebiet der beschreibenden Naturwissenschaften hinüber und bildet dadurch eine Brücke zwischen den exakten und den beschreibenden Naturwissenschaften, das bisher fehlende Verbindungsglied zwischen der Himmelsmechanik und der Geologie.
Belgrad, März 1941.
M. Milankovitch
Erster Abschnitt
Die Bewegung der Planeten um die Sonne und die gegenseitigen Störungen dieser Bewegung
Kapitel I
Das Newtonsche Gravitationsgesetz
§ 1. Die Keplerschen Gesetze. Ich habe in meinen beiden im Vorwort angeführten Schriften "Stellung und Bewegung der Erde im Weltall" und "Mechanik des Himmels" den geschichtlichen Entwicklungsgang unserer Kentnisse von der Bewegung der Himmelskörper ausführlich geschildert. Indem ich auf diese historische Studie verweise, möchte ich einiges davon hier kurz erwähnen. Der auf Jahrtausende sich erstreckenden ununterbrochenen Tätigkeit der chaldäischen Himmelsbeobachter ist es zu danken, dass eine Fülle astronomischen Tatsachenmaterials zu Tage gefördert wurde. mit dem die alten Griechen und Alexandriner das antike Gebäude der astronomischen Wissenschaft errichten konnten, Die Pythagoräer lehrten die Kugelgestalt der Erde, später auch ihre Drehbewegung. Aristote1es bewies jene Kugelgestalt, und aus der Anschauung einer sich drehenden Erde entwickelte sich nach und nach das heliozentrische Weltsystem der Alten, das durch Aristarch von Samos zum vollständigen Ausbau gebracht wurde, denn "er liess den Fixsternhimmel feststehen, dagegen die Erde sich auf einen gegen den Aequator geneigten Kreise bewegen und gleichzeitig um ihre Achse drehen".
Sonderbar waren die Schicksale dieses antiken heliozentrischen Weltsystems. Ich glaube in meiner Studie zur Genüge bewiesen zu haben, dass Apo11onios von Perge durch die Beantwortung der naheliegenden Frage, wie die Bewegungen der Planeten im Aristarch′schen Weltsystem verlaufen müssten, wenn man sie von der Erde aus verfolge, seine Theorie der Epizyklen geschaffen hat. Diese Epizyklen stellten also die relativen Bahnen der Planeten in bezug auf die Erde dar und konnten deshalb im geozentrischen Weltsystem des Pto1emaios ausgiebige Verwendung finden, die das heliozentrische Weltsystem in den Hintergrund, ja in gänzliche Vergessenheit zurückdrängte. Erst Kopernikus gelang es, den Knäuel der Epizyklen zu entwirren und das Gebäude des heliozentrischen Weltsystems wieder zu errichten. Galilei brachte dasselbe zur Anerkennung und Kepler entdeckte die kinematischen Gesetze der Planetenbewegung. Ich habe in den erwähnten Schriften berichtet, wie Kep1er die Himmelsbeobachtungen des Tycho Brahe genial verwertend seine Gesetze abgeleitet hat. Diese Gesetze sind bekanntlich die folgenden:
- Die Planeten beschreiben um die Sonne Ellipsen, in derem gemeinsamen Brennpunkte die Sonne steht.
- Der Radiusvektor von der Sonne nach dem Planeten hin überstreicht dabei in gleichen Zeiten gleiche Flächen.
- Die Quadrate der Umlaufszeiten der Planeten verhalten sich zu einander wie die dritten Potenzen der grossen Halbachsen ihrer Bahnellipsen.

Es ist notwendig, diese Gesetze in mathematische Formeln zu kleiden, weil davon oft Gebrauch zu machen sein wird. Dabei ist unter der Bahn des Planeten jene seines Schwerpunktes zu verstehen.
Es stelle also BCADB (Fig. 1) die Bahnellipse des in Betracht gezogenen Planeten dar. AB sei die grosse, CD die kleine Achse derselben. S und F seien die beiden Brennpunkte dieser Ellipse, wobei S derjenige dieser Brennpunkte sein möge, den die Sonne umschliesst; dann heisst B das Perihelium und A das Aphelium der Planetenbahn. Bezeichnet a die grosse, b die kleine Halbachse der Ellipse, es ist GS = OF = √(a2 + b2). Die unbenannte Zahl
| (1) |  |
Wird die numerische Exzentrizität oder kurz die Exzentrizität der Planetenbahn genannt. Es ist
- (2) b2 = a2 · (1 - e2)
Die Länge
- (3) p = b2 ⁄ a
- (4) p = a · (1 - e2)
wird der Parameter der Bahnellipse genannt.
Verbindet man einen beliebigen Punkt M der Bahnellipse, d.h. eine beliebige Lage des Planeten auf dieser Bahn mit den beiden Brennpunkten S und F und bezeichnet die beiden Radiusvektoren SM bzw. FM mit r bzw. r1, so ist nach der Definition der Ellipse
- r + r1 = 2 · a.
Der mit ν bezeichnete Winkel BSM wird die wahre Anomalie des in der Lage M gedachten Planeten genannt.
Es folgt aus dem Dreieck FSM, in dem nach dem soeben gesagten FS = 2 · e · a ist,
- r12 = (2 · e · a)2 + r2 + 4· e · a · r · cos ν.
Setzt man hierin für r1 = 2a - r
ein, so wird
- (1 + e · cos ν) · a · r = 2 - e2 · a2 = b2,
d. h.
| (5) |  |
Dies ist die Gleichung der Planetenbahnellipse und der mathematische Ausdruck des ersten Keplerschen Gesetzes.
Für ν = π ⁄ 2 wird r = p, woraus die Bedeutung des Parameters p ersichtlich ist: seine Länge ist gleich jener des auf der grossen Bahnachse senkrechten Radiusvektors.
Um das zweite Keplersche Gesetz mathematisch zum Ausdruck zu bringen, sei dν die dem unendlich kleinen Zeitintervall dt entsprechende Zunahme der wahren Anomalie. Während dieser Zeit überstreicht der Radiusvektor r die Fläche dF = ½ · r2dν des unendlich schmalen Dreiecks MSM'. Der Quotient
wird die Flächengeschwindigkeit der Bewegung genannt; diese soll dem zweiten Keplerschen Gesetz zufolge konstant sein. Es ist deshalb
worin C eine der doppelten Flächengeschwindigkeit gleiche Konstante bedeutet. Es folgt aus den vorstehenden Gleichungen
| (6) |  |
wodurch das zweite Keplersche Gesetz mathematisch in Differentialform ausgedrückt erscheint.
Bezeichnet T die Umlaufszeit des Planeten um die Sonne, so wird während dieser Zeit die ganze von der Bahnellipse umschlossene Fläche ζab überstrichen. Die Flächengeschwindigkeit erscheint also auch durch den Ausdruck
dargestellt. Es ist also
| (7) |  |
Das dritte Keplersche Gesetz ist mathematisch durch die Gleichung
| (8) |  |
veranschaulicht, in der k für alle Planeten eine und dieselbe Grösse ist.
Durch die Gleichungen (5) und (6) ist die Bewegung des Planeten auf seiner Bahn eindeutig gegeben und es lässt sich durch Integration dieser Gleichungen die Lage des Planeten auf dieser Bahn in endlicher Form als Funktion der Zeit darstellen. Kepler hat dieses Problem durch geometrische Überlegungen gelöst, die ihre Bedeutung bis heute bewahrt haben, weshalb sie hier wiedergegeben werden mögen.
…
§ 2. Ableitung des Gravitationsgesetzes aus den Keplerschen Gesetzen. Hochbedeutend waren die Schlüsse: die Isaac Newton aus den Keplerschen Gesetzen zog und in seinen "Philosophiae naturalis principia mathematica, London 1687" veröffentlichte, nachdem es ihm durch dieses Werk gelungen war, den von Ga1i1ei und Huyghens begonnenen Aufbau der Mechanik zum epochemachenden Abschluss zu bringen. Seine Schlussfolgerungen, in die Sprache der modernen Vektoranalysis übertragen, sind die folgenden.

Ein Massenpunkt bewege sich unter dem Einflusse sonst beliebiger Kräfte in einer Ebene, in der der Pol 0 und die Achse O-X eines polaren Koordinatensystems nach Belieben festgelegt werden mögen. Seien r und ν die zugehörigen Koordinaten einer beliebig gewählten Lage M des sich bewegenden Massenpunktes und 𝔯 dessen auf den Punkt 0 sich beziehender Ortsvektor.
Vektorgrössen sollen in Hinkunft durch gotische, Skalargrössen durch lateinische oder griechische Buchstaben bezeichnet werden; der einem Vektor zugehörige Einheitsvektor soll durch den Index Null gekennzeichnet werden. Es ist also
| (16) | 𝔯 = r · 𝔯0 |
worin 𝔯0 den Einheitsvektor der Richtung 𝔯 bedeutet.
Bildet man die Ableitung des vorstehenden Ausdruckes nach der Zeit t, so wird
Die linke Seite dieser Gleichung stellt den Geschwindigkeitsvektor
| (17) |
 |
des in Betracht gezogenen Massenpunktes dar. Ebenso stellt d𝔯0 ⁄ dt den Geschwindigkeitsvektor des Endpunktes des Einheitsvektors 𝔯0 infolge der Aenderung des Winkels ν dar. Bezeichnet also 𝔫0 den auf dem Vektor 𝔯 senkrecht stehenden, in der Bahnebene gelegenen Einheitsvektor, der nach der Seite des wachsenden ν gerichtet ist, so ist jener Geschwindigkeitsvektor dargestellt durch:
| (18) |
 |
Es wird also
| (19) |
 |
Setzt man
| (20) |
 |
So bekommt man
| (21) |
 |
Es stellen also vr und vn die Komponenten des Geschwindigkeitsvektors 𝔳 in der Richtung 𝔯0 bzw. 𝔫0 dar.
Die Differentiation des Ausdruckes (19) nach der Zeit t ergibt:
Dieselben Betrachtungen, die man bei der Niederschrift von (18) angestellt hat, ergeben
so dass man bekommt:
oder, weil
ist,
| (22) |
 |
Die linke Seite dieser Gleichung stellt den Beschleunigungsvektor
| (23) |
 |
des in Betracht gezogenen Massenpunktes dar. Setzt man
| (24) |
 |
so bekommt man
| (25) | 𝔭 = pr · 𝔯0 + pn · 𝔫0 |
Es stellen also pr und pn die Komponenten des Beschleunigungsvektors 𝔭 in der Richtung von 𝔯0 bzw. 𝔫0 dar.
Wenden wir nun die soeben gewonnenen Gleichungen auf die Bewegung eines unter dem alleinigen Einflusse der Sonne stehenden Planeten an! Legen wir dabei den Pol O unseres Koordinatensystems in den Mittelpunkt der vorläufig ruhend gedachten Sonne und richten wir dessen Achse gegen das Perihelium. Dann kommt den Grössen r und ν die ihnen im vorigen Paragraphen gegebene Bedeutung zu und es ist deshalb nach (6)
worin C eine von der Zeit unabhängige Grösse bedeutet. Setzt man dies in (24) ein, so wird
| (26) | pn = 0 |
Dies bedeutet, dass der Beschleunigungsvektor des Planeten in jedem Punkte seiner Bahn in der Verbindungsgeraden des Planeten mit der Sonne gelegen ist. Um die skalare Grösse und die Richtung dieses Beschleunigungsvektors auf die einfachste Weise zu ermitteln, soll wie folgt verfahren werden.
Weil
und
ist, so wird
Setzt man die beiden vorstehenden Ausdrücke in (24) ein, so bekommt man die nachstehende von Binet herrührende Formel
| (27) |
 |
Es folgt aus dem ersten Keplerschen Gesetze, also aus (5),
d. h.
also
Setzt man dies in (27) ein, so wird
Zieht man (3) und (7) heran, so bekommt man
| (28) |
 |
oder wegen (8)
Die Konstante k ist, wie bereits angegeben, für alle Planeten eine und dieselbe, was für
ebenfalls der Fall ist. Es ist deshalb
Setzt man dies in (26) und (25) ein, so bekommt man
| (29) |
 |
Diese Gleichung besagt, dass alle Planeten in jeder Lage auf ihrer Bahn einer gegen die Sonne gerichteten Beschleunigung unterliegen, deren skalare Grösse dem Quadrat des Abstandes von der Sonne umgekehrt proportional ist.
Bei diesem Ergebnis angelangt, ging Newton mit grosser Kühnheit des Gedankens weiter. Er erkannte, und zwar an dem BeispieI des Erdmondes, dass jene sich kundgebende Beschleunigung ihrem Wesen nach identisch ist mit der uns bekannten Schwerebeschleunigung. Newton nahm also an, die von der Erde ausgehende Wirkung, die sich in der Beschleunigung fallender Körper äussert, reiche in die Himmelsräume, also auch bis zum Erdmond. Um dies zu ersehen, stellte er folgende Berechnung an. Auf der Erdoberfläche, d. h. in einer Entfernung R vom Erdmittelpunkt, wo R den Radius der Erdkugel bedeutet, erleiden schwere Körper eine Beschleunigung g, die nach den Messungen von Galilei etwas über 30 Fuss pro sec2 beträgt. In der Entfernung r des Mondes von der Erde beträgt diese Beschleunigung, weil sie mit dem Quadrat der Entfernung abnimmt,
- (R2 ⁄ r2) · g.
Wenn also für die Bewegung des Mondes um die Erde dasselbe Gesetz gilt wie für die Bewegung der Planeten um die Sonne, dann muss nach (28) der absolute Wert jener Beschleunigung durch den Ausdruck dargestellt sein:
-
 .
.
worin T die Umlaufszeit des Mondes um die Erde und a die grosse Halbachse der Mondbahn bedeutet. Aus den vorstehenden zwei Ausdrücken folgt weiter:
-
 .
.
Mit Hilfe dieser Gleichung konnte Newton die Schwerebeschleunigung g aus den numerischen Werten der Grössen R, a, T berechnen. Das Rechnungsergebnis stimmte mit der von Ga1i1ei ermittelten Grösse der Schwerebeschleunigung überein, wodurch die Richtigkeit des Newtonschen Gedankens erwiesen wurde.
Auch bei diesem grundlegenden Ergebnisse blieb Newtons Genie nicht stehen. Nachdem er erkannt hatte, dass ein und derselbe Körper, je nach seiner Entfernung vom Erdmittelpunkte, eine verschiedene Beschleunigung erleide, d. h. ein verschiedenes Gewicht aufweise, führte Newton den Begriff der Masse ein, die, als das eigentliche Merkmal des Körpers, unveränderlich ist. Damit trennte Newton als erster klar die Begriffe Masse und Gewicht. Dieses letztere definierte er als Produkt von Masse und Schwerebeschleunigung. Damit war auch der allgemeine Begriff der Kraft gewonnen, die dem Produkt der Masse und der dem Körper erteilten Beschleunigung gleich ist. Zu gleicher Zeit stellte Newton auch sein grundlegendes Prinzip der Gleichheit von Wirkung und Gegenwirkung auf. Als Folge dieser Klarlegung der Begriffe ergab sich die nachstehende Überlegung.
Multipliziert man die Gleichung (29) mit der Masse m des in Betracht gezogenen Planeten, so erhält man links das Produkt der Masse und der Beschleunigung des Planeten, also die auf den Planeten wirkende Kraft:
| (30) |
 |
Diese Kraft ist wegen des hier vorkommenden Vorzeichen minus gegen die Sonne gerichtet und stellt deshalb die von der Sonne auf den Planeten ausgeübte Anziehungskraft dar. Nach dem Prinzip der Wirkung und Gegenwirkung übt der Planet seinerseits auf die Sonne dieselbe anziehende Wirkung aus, und diese muss nach dem soeben klargelegten Kraftbegriff proportional sein der Masse M der Sonne. Führt man also eine neue Grösse f, die durch die Gleichung
| (31) | f = μ ⁄ M |
oder
| (32) |
 |
definiert erscheint, ein, so bekommt man statt (30)
| (33) |
 |
Der Faktor f wies einen und denselben numerischen Wert für alle Planeten auf, ja er galt in der ihm durch (32) verliehenen Bedeutung auch für den Mond and die Schwere. Es stellt also f eine für das ganze Sonnensystem geltende Konstante dar, die eine allgemeine Eigenschaft der in diesem System befindlichen Materie zum Ausdruck bringt. Zu dieser Erkenntnis angelangt, konnte Newton noch einen gewaltigen Schritt machend, behaupten, dass die Gleichung (33) für alle Teile der im Weltraum angehäuften Materie giltig ist und sein Gesetz der allgemeinen Gavitation aufstellen. Nach demselben zieht jedes Teilchen der Materie im Weltall jedes andere Teilchen instantan mit einer Kraft an, die in der Verbindungslinie der beiden Teilchen gelegen ist und deren Grösse sich direkt wie das Produkt der Massen m1 und mw beider Teilchen und umgekehrt wie das Quadrat ihres Abstandes r verhält, also durch
-
 .
.
dargestellt erscheint. Dabei ist der Proportionalitätsfaktor f eine universelle Konstante. Im obigen Ausdruck ist das Vorzeichen minus fortgefallen, weil durch die Worte "zieht an" die Richtung der Kraft eindeutig gegeben ist.
Durch das Newtonsche Gesetz ward das tausendjährige Rätsel der Planetenbewegung gelöst und eine ganze Reihe neuer Erkenntnisse flossen wie von selbst aus demselben. Alle beobachteten Ungleichheiten in der Bewegung der Planeten und des Mondes erwiesen sich als natürliche Folge jenes Gesetzes, indem sie nur die gegenseitige Anziehung dieser Weltkörper zum Ausdruck brachten. Damit erschien aber nicht nur ihr Wesen geklärt, diese Ungleichheiten liessen sich in vorhinein exakt berechnen. Es zeigte sich, und zwar für die Kometen sehr bald, dass auch die übrigen und auch ausserhalb des Planetensystems sich bewegenden Weltkörper dem Newtonschen Gravitationsgesetz gehorchen. Die von Hipparchos entdeckte Präzession der Nachtgleichen fand ihre vollständige mechanische Erklärung, desgleichen die von Bradley später entdeckte Nutation der Erdachse. Auch die Gestalt der Erde, insbesondere deren Abplattung durch die Rotation, wurde mathematisch ergründet und das uralte Problem des Flutphänomens fand seine Lösung in der Anziehung der beweglichen Wassermassen durch Mond und Sonne. So erwies sich das Newtonsche Gravitationsgesetz, das grossartigste, das zu erkennen es einem Sterblichen vergönnt war, als ein allgemeines, das Weltall beherrschende Naturgesetz. Diesem Gesetz entspross eine neue Wissenschaft, die Mechanik des Himmels. Die dem Ziele dieses Werkes führenden Lehren dieser Wissenschaft sollen in dem im Vorwort angegebenen Sinne nachstehend zur Behandlung und Anwendung gelangen.
Kapitel II
Das Zweikörperproblem der Himmelsmechanik und die ungestörte heliozentrische Bewegung der Planeten
§ 3. Problemstellung. Obwohl sich alle Mitglieder unseres Planetensystems ggenseitig anziehen, erfolgt die jährliche Bewegung eines jeden Planeten fast gerade so, als ob derselbe nur der Anziehung der Sonne uuterworfen wäre. Wegen der überwältigenden Grösse der Sonnenmasse gegenüber den Massen aller Planeten ist die gegenseitige Anziehung dieser letzteren im Vergleich zur Anziehungskraft der Sonne derart unbedeutend, dass ihre Wirkung auf die Bewegung der Planetencnur als eine geringfügige Störung empfunden wird, die sich erst nach Verlauf längerer Zeitintervalle fühlbar macht. Deshalb bildet das sogenannte Zweikörperproblem den Ausgangspunkt der Lehre von der Bewegung der Planeten. Dasselbe besteht in folgender Aufgabestellung: Zwei Himmelskörper ziehen sich gegenseitig nach dem Newtonschen Gravitationsgesetz an; man ermittle aus gegebenen Anfangsbedingungen die Bewegung dieser beiden Himmelskörper in bezug auf ein ruhend gedachtes Bezugssystem.
Um unbeschadet der Allgemeinheit der nachstehenden Erörterungen einen konkreten Fall vor sich zu haben, seien die beiden Himmelskörper die Sonne und ein beliebiger Planet. Die Masse der Sonne sei mit M, die Masse des Planeten mit m bezeichnet; der Ortsvektor von M sei mit 𝕽, der Ortsvektor von m mit 𝖑 bezeichnet. Die relative Lage von m in bezug auf M ist dann durch den Ortsvektor
| (34) |
 |
gegeben.
Stellt, wie vereinbart, r den Modul, d h. die skalare Grösse des Vektors 𝖗 dar, dann erscheint der Einheitsvektor der Richtung 𝖗 durch
| (35) |
 |
veranschaulicht. Die Kraft, mit der die Sonne M den Planeten m anzieht, ist nach (33) und (35) dargestellt durch -f(M · m ⁄ r3) · 𝖗, und jene, mit der der Planet auf die Sonne wirkt, dargestellt durch +f(M · m ⁄ r3) · 𝖗. Es sind deshalb die vektoriellen Bewegungsgleichungen dieser beiden Himmelskörper die folgenden:
| (36) |
 |
|
| (37) |
 |
wo t die Zeit bedeutet.
Diese zwei vektoriellen Differentialgleichungen zweiter Ordnung sind sechs skalaren Differentialgleichungen gleicher Ordnung gleichwertig und besitzen 12 skalare Integrale; es handelt sich darum, diese zu finden.
§ 4. Die Schwerpunktsintegrale. Sei S der gemeinsame Schwerpunkt, besser gesagt Massenmittelpunkt der Massen M und m, 𝕾 der Ortsvektor dieses Punktes. Gemäss der Definition eines solchen Massenmittelpunktes ist dessen Ortsvektor gegeben durch
| (38) |
 |
Zweimalige Differentiation dieser Vektorgleichung nach t liefert die Gleichungen:
| (39) |
 |
|
| (40) |
 |
Weil nun, wie die Addition von (36) und (37) ergibt, die rechte Seite von (40) gleich Null ist, so wird
| (41) |
 |
Dieser Ausdruck stellt den Beschleunigungsvektor des Massenmittelpunktes S dar, und weil derselbe ständig gleich Null ist, so bewegt sich dieser Punkt geradlinig und gleichförmig.
Die Integration der vorstehenden Differentialgleichung ergibt:
| (42) |
 |
wo 𝕭 ein von der Zeit t unabhängiger Vektor ist und den Geschwindigkeitsvektor des Massenmittelpunktes S veranschaulicht. Das Integral der vorstehenden Differentialgleichung lautet
| (43) |
 |
und stellt die in endlicher Form geschriebene Bewegungsgleichung des Punktes S dar.
Die Gleichungen (42) und (43) siellen die sogenannten Schwerpunktsintegrale in vektorieller Form dar: sie sind sechs skalaren Integralen gleichwertig. Die hier vorkommenden Konstanten 𝕬 und 𝕭 ergeben sich aus den Anfangsbedingungen, worunter die Ortsvektorer 🕽0 und 𝖑0 der beiden Massenkörper M und m und deren Anfangsgeschwindigkeiten 𝖜0 und 𝖛0 zu verstehen sind. Sind diese vier Vektoren gegeben, dann ergibt sich aus (38) der Ortsvektor 𝕬 der Anfangslage des Punktes S, und aus (39) dessen Geschwindigkeitsvektor 𝕭.
Nachdem durch die vorstehenden Integrale die Bewegung des Massenmittelpunktes der beiden Himmelskörper M und m beschrieben worden ist, kann das gestellte Problem in dem Sinn eingeschränkt werden, dass man von nun an nur nach der relativen Bewegung von m in bezug auf M, also nach der ungestörten heliozentrischen Bewegung des in Betracht gezogenen Plnneten frägt, weil durch diese relative Bewegung vermittels der bereits gewonnenen Integrale auch die absolute Bewegung von M und m in dem unseren Betrachtungen zugrunde gelegten Bezugssystem gegeben ist.
§ 5. Die beiden Vektorintegrale der Differentialgleichung der ungestörten heliozentrischen Bewegung der Planeten.
§ 6. Geometrische Deutung der beiden Vektorintegrale. Es folgt aus (49) und (48)
 |
Dabei stellt d𝖗 die während des Zeitintervalles dt vom Planeten relativ zur Sonne zurückgelegte Strecke, und [𝖗d𝖗] einen Vektor dar, der auf der Ebene der Vektoren 𝖗 und d𝖗 senkrecht stehend, nach jener Seite dieser Ebene gerichtet ist, von der aus betrachtet die Bewegung des Planeten rechtläufig erfolgt, und der eine skalare Grösse aufweist, die gleich ist der Fläche des durch 𝖗 und d𝖗 begrenzten Parallelogramms. Diese Fläche ist aber nichts anderes als das Zweifache des vom Leitstrahl Sonne-Planet während der Zeit dt überstrichenen Flächenelements dF. Der Vektor 𝕮 stellt also die doppelte Flächengeschwindigkeit der Planetenbewegung vektoriell dar. Das Vektorintegral (49) drückt also das zweite Keplersche Gesetz in Vektorform aus, indem es besagt, dass die vom Leitstrahl 𝖗 in der Zeiteinheit überstrichene Fläche nicht nur ihrem Betrage nach konstant ist, sondern auch ihrer räumlichen Orientierung nach. Es erfolgt also die Bewegung des Planeten um die Sonne mit einer konstanten Flächengeschwindigkeit in einer Ebene, die durch den Sonnenmittelpunkt hindurchgeht und auf dem Vektor 𝕮 senkrecht steht. Durch den Vektor 𝕮 ist die Bahnebene des Planeten, seine Umlaufsrichtung und die Flächengeschwindigkeit seiner Bewegung eindeutig gegeben.
Multipliziert man die Gleichung (49) skalar mit 𝖗 bzw. mit 𝖛, so bekommt man die Gleichungen:
| (53) |
 |
|
| (54) |
 |
die das vorher gesagte ebenfalls zum Ausdruck bringen.
Multipliziert man die Gleichung (52) skalar mit 𝕮, dann bekommt man wegen (53)
| (55) |
 |
Der Vektor 𝕯 steht also senkrecht auf dem Vektor 𝕮 und gehört der Hahneben des Planeten an.
Die Gleichung (53) stellt vektoranalytisch diese Bahnebene dar. In der Tat: führt man ein orthogonales Koordinatensystem ein, dessen Ursprung im Mittelpunkt der Sonne gelegen und gegen den Fixsternhimmel unveränderlich orientiert ist, weshalb wir es als das "ruhende" bezeichnen wollen, und bezeichnet man mit 𝖓1, 𝖓2, 𝖓3 die Einheitsvektoren der Achsenrichtungen dieses Systems, mit x, y, z die Koordinaten des Planeten und mit C1, C2, C3 die Koordinaten des Vektors 𝕮, so ist
| (56) |
 |
|
| (57) |
 |
Setzt man dies in (53) ein, so bekommt man
| (58) |
 |
Dies ist die analytische Gleichung der ßahnebene des Planeten.
Multipliziert man die Gleichung (52) skalar mit 𝖗, so bekommt man
 |
und, weil
 |
ist, worin C den Modul des Vektors 𝕮 bedeutet, so wird
| (59) |
 |
Diese Gleichung stellt vektoranalytisch eine Fläche zweiter Ordnung dar. Bezeichnet man nämlich mit D1, D2, D3 die Koordinaten des Vektors 𝕯), so wird
| (60) |
 |
Setzt man dies, (56) und
| (61) |
 |
in (59) ein, so bekommt man
| (62) |
 |
und dies ist tatsächlich die analytische Gleichung einer Fläche zweiter Ordnung.
Die Gleichungen (58) und (62) stellen also einen Kegelschnitt, die Bahnkurve des Planeten, dar; die Gleichungen (53) und (59) stellen diese Kurve vektoranalytisch dar.
Um die Gleichung der Bahnkurve des Planeten in einer für unsere Zwecke entsprechenden Form zu erhalten, führen wir noch ein zweites Koordinatensystem ξ - η - ζ ein, dessen Ursprung ebenfalls in den Sonnenmittelpunkt gelegt sein möge, dessen ξ-Achse die Richtung des Vektors 𝕯 und dessen ζ-Achse die Richtung des Vektors 𝕮 aufweisen soll. Weil die Einheitsvektoren der Richtungen 𝕮 und 𝕯 durch
| (63) |
 |
dargestellt erscheinen, so sind die Einheitsvektoren der Achsenrichtungen des Koordinatensystems ξ - η - ζ, das wie jenes zuerst benutztes ein englisches sein möge, durch die nachstehenden Ausdrücke veranschaulicht:
| (64) |
 |
Die Koordinaten des Ortsvektors 𝕧, also die Koordinaten des Planeten bezüglich des neuen Koordinatensystems seien mit ξ, η, ζ bezeichnet, so dass geschrieben werden kann:
 |
Multipliziert man diese Gleichung, skalar mit 𝖐, so wird wegen (53), (63), (64)
 |
d. h.
| (65) |
 |
|
| (66) |
 |
Multipliziert man diese Gleichung skalar mit 𝕯, so wird:
| (67) |
 |
also wegen (59)
| (68) |
 |
Dies ist die Gleichung der Bahnkurve des Planeten, ausgedrückt in Semipolarkoordinaten ζ und 𝖗.
Die vorstehende Gleichung kann leicht auf Polarkoordinaten r und ν transformiert werden, denn es ist
| (69) |
 |
so dass man statt (68) die folgende Gleichung erhält
 |
d. h.
| (70) |
 |
Vergleicht man diese Gleichung mit (5) und setzt voraus, dass, was für alle Planeten der Fall ist, D ⁄ μ > 0 ist, so ersieht man, dass die Bahnkurve des Planeten eine Ellipse ist. Die grosse Achse dieser Ellipse fällt in die hier gewählte ξ-Achse, deren positiver Ast gegen das Perihelium gerichtet ist. Weil die ξ-Achse aber in die Richtung des Vektors 𝕯 gelegt worden ist, so ergibt sich daraus die wichtige Eigenschaft dieses Vektor,. dass er gegen das Perihelium gerichtet ist. Der Vergleich der Gleichungen (70) und (5) ergibt auch, dass der Parameter p der Bahnellipse gleich ist
| (71) |
 |
und deren Exzentrizität gleich ist
| (72) |
 |
Es ist also
| (73) |
 |
Durch die vorstehenden Ergebnisse ist die grundlegende Bedeutung der Vektoren 𝕮 und 𝕯 klar zu Tage getreten; sie ist in der Fig. 4 geometrisch veranschaulicht. In derselben stellt die Ellipse AP die Bahn des Planeten dar. Der von der Sonne eingenommene Brennpunkt der Bahnellipse ist zum Ursprung des ruhenden Koordinatensystems gewählt worden. Die durch O hindurchgehende Bahnebene des Planeten ist gegen dieses Koordinatensystem schräg gerichtet. Der Vektor 𝕮 steht senkrecht auf dieser Ebene. der Vektor 𝕯 in dieser Ebene gelegen, ist gegen das Perihelium P dieser Bahn gerichtet. Durch den Vektor 𝕮 erscheint die Bahnebene des Planeten festgelegt, die Umlaufsrichtung der Planetenbewegung und der Parameter der Bahnellipse gegeben; durch den Vektor 𝕯 ist die Achsenlinie der Bahnkurve in ihrer Ebene festgelegt und die Exzentrizität dieser Bahn gegeben.

Die Koordinaten C1, C2, C3; D1, D2, D3 der Vektoren 𝕮 und 𝕯, die eine hervorragende Rolle auch in der Störungsrechnung spielen werden, will ich die vektoriellen Elemente der Planetenbewegung nennen. Von diesen sechs Elementen sind nur fünf voneinander unabhängig setzt man nämlich (57) und (60) in (55) ein, so bekommt man
| (74) |
 |
und dieser Gleichung müssen die angeführten Elemente Genüge leisten.
Die Vektorgleichungen (49) und (52) liefern also nur fünf voneinander unabhängige skalare Integrale der Differentialgleichung (47). Weil diese Gleichung sechs skalare Integrale besitzt, so bleibt zur vollständigen Lösung des gestellten Problems noch übrig, das fehlende sechste Integral dieser Gleichung zu finden. Vorher mögen aus den gewonnenen vektoriellen Integralen noch einige Folgerungen gezogen werden.
§ 7. Verschiedene andere Formen der erhaltenen Integrale.
§ 8. Das sechste skalare Integral.
§ 9. Endgültige vektorielle Form der vollständigen Integrale der Differentialgleichung der ungestörten Bewegung der Planeten.
§ 10. Das Satellitenproblem, zurückgeführt auf das Zweikörperproblem.
§ 11. Der Zusammenhang zwischen den vektoriellen und den elliptischen Elementen. Der im engen Zusammenhange mit den astronomischen Beobachtungen sich vollziehende Ausbau der Theorie der Planetenbewegung brachte es mit sich, dass auch in dieser Theorie von ihrem Anfang an die bei jenen Beobachtungen in Gebrauch stehenden elliptischen Elemente Benützung fanden, obwohl sie dem Wesen dieses mechanischen Problems eigentlich fremd sind. Die Wissenschaft der Himmelsmechanik wurde auf diese Weise mittels dieser Elemente erbaut, weshalb es erforderlich ist, den Zusammenhang zwischen diesen elliptischen Elementen und den hier zur Verwendung gelangten vektoriellen Elementen herzustellen.

Bei den vorstehenden Untersuchungen wurde über die räumliche Orientierung des dabei benützten "ruhenden" Koordinatensystems X-Y-Z, das seinen Ursprung in der Sonne hatte und ein orthogonales war, keine besondere Vereinbarung getroffen, weil dies für diese theoretischen Untersuchungen nicht erforderlich gewesen ist; für die praktischen Anwendungen der Himmelsmechanik muss ein exakt determiniertes Koordinatensystem gewählt werden. Als ein solches wird ein orthogonales, englisches Koordinatensystem benützt, dessen X-Y-Ebene mit der einer bestimmten Epoche (gewöhnlich 1.0 Januar 1900) zugehörigen Ebene der Erdbahn zusammenfällt, dessen X-Achse gegen den Frühlingspunkt dieser Epoche und dessen Z-Achse gegen den Nordpol der Ekliptik gerichtet ist. Der positive Drehsinn eines solchen Systems, d. h. die von dem positiven Aste der Z-Achse beobachtete Drehung, die auf dem kürzesten Wege den positiven Ast der X-Achse mit dem positiven Ast der Y-Achse zur Koinzidenz bringt, stimmt mit dem Umlaufssinn der Planeten überein. Dieses Koordinatensystem sei in der Fig. 5 veranschaulicht. Seine Achsen durchdringen die scheinbare Himmelssphäre in den Punkten N1, N2, N3, wobei der Punkt N1 den erwähnten Frühlingspunkt bedeutet. Der grösste Kreis ☊ ⁄ ☋ der Himmelssphäre (die in der Figur nur mit ihrer über der X-Y-Ebene liegenden Hälfte dargestellt erscheint) stelle den Schnitt der Bahnebene des in Betracht gezogenen Planeten mit der Himmelssphäre dar. Diese Ebene der Planetenbahn schneidet die X-Y-Ebene des Koordinatensystems längs der durch seinen Ursprung O gehenden Geraden ☊ ⁄ ☋, die die Knotenlinie genannt wird. Der Durchstosspunkt ⚚ dieser Geraden mit der Himmelssphäre, in dem der Planet oberhalb der X-Y-Ebene aufsteigt, heisst der aufsteigende Knoten. Der Winkel, den der nach ⚚ gerichtete Halbstrahl der Knotenlinie mit der X-Achse einschliesst, also der Bogen N, ⚚ der Himmelssphäre, wird die Länge des aufsteigenden Knotens genannt. Wir werden diese Grösse stets mit Ω bezeichnen. Die Bahnebene des Planeten schliesst mit der X- Y-Ebene unseres Koordinatensystems den spitzen Winkel i ein, der die Neigung der Bahnebene genannt wird. Er ist in der Figur durch den sphärischen Winkel N2 ⚚ I veranschaulicht. Durch die Elemente Ω und i ist die Bahnebene des Planeten eindeutig festgelegt. Um die Orientierung der Bahnellipse, deren einer der Brennpunkte in O gelegen ist, in ihrer Ebene festzulegen, projiziere man das Perihelium der Planetenbahn vom Punkte O aus auf die Himmelssphäre. Der Punkt I der Himmelsphäre, der notwendigerweise auf dem Kreise ☊ ⁄ ☋ liegen muss, stelle diese Projektion dar. Dann heisst der Bogen ☊ I der Himmelssphäre, der mit ω bezeichnet werden möge, die Länge des Perihels, gemessen vom aufsteigenden Knoten. Durch denselben ist die Orientierung der Bahnellipse eindeutig gegeben; in der astronomischen Praxis geschieht dies durch die Summe der nicht in demselben Hauptschnitt der Himmelssphäre liegenden Bogen N1 ☊ und ☊ I, also durch Ω + ω. Diese Summe wird kurz die Länge des Perihels genannt; sie möge mit Π bezeichnet werden. Es ist also
| (109) |
 |
Die Bahnellipse selbst ist durch ihre grosse Halbachse a und ihre numerische Exzentrizität e eindeutig bestimmt. Durch die Grösse a ist, bei gegebenen Massen M und m, auch die mittlere Bewegung n des Planeten vermittels (81) und mit (80) seine siderische Umlauszeit T gegeben.
Die Grösse
| (110) |
 |
wird die mittlere Anomalie des Planeten genannt. Es ist dies die wahre Anomalie jenes fiktiven Planeten, der sich in der Ebene der Planetenbahn auf einem Kreise um die Sonne mit konstanter Winkelgeschwindigkeit n bewegen und gleichzeitig mit dem wahren Planeten die grosse Achse seiner Bahn durchschreiten würde. Demzufolge wird
| (111) |
 |
die wahre Länge des Planeten, und
| (112) |
 |
die mittlere Länge des Planeten genannt.
Im Initialmoment t = 0, d. h. zu der bereits festgelegten Epoche, von der die Zeit gezählt wird, weist l den Wert
| (113) |
 |
auf. Dieser Wert, die mittlere Länge der Epoche genannt, liefert das gewünschte sechste Element.
Die sechs Elemente
Ω, i, Π, a, e, ε
werden die elliptischen Elemente der heliozentrischen Bewegung der Planeten genannt.
Es soll nun der Zusammenhang zwischen diesen elliptischen Elementen und vorstehend benützten vektoriellen Elementen ermittelt werden.
Sei ξ—3—ζ das bei den vorstehenden Untersuchungen benützte orthogonale Koordinatensystem, dessen ξ-Achse mit dem Vektor 𝕯 und dessen ζ-Achse mit dem Vektor 𝕮 zusammenfällt. Weil der Vektor 𝕯gegen das Perihelium gerichtet ist, durchdringt die Achse ξ dieses Koordinatensystems die scheinbare Himmelssphäre im Pukte I; weil der Vektor 𝕮 auf der Ebene der Planetenbahn senkrecht steht, schliesst er und damit die Achse ζ mit der Achse Z des Koordinatensystems X-Y-Z denselben Winkel i ein, den die Bahnebene des Planeten mit der X-Y-Ebene einschliesst. Bezeichnet also K den Durchstosspunkt der Achse ζ mit der Himmelssphäre, so ist der Winkel N3OK und damit auch der Bogen N3K der Himmelssphäre gleich i.
Nach diesen Feststellungen ergibt sich folgendes. Die Koordinate C3 des Vektors 𝕮 ist gleich
| (114) |
 |
während die in die X-Y-Ebene fallende Projektion des Vektors 𝕮 eine skalare Grösse Ca aufweist, die durch
 |
dargestellt ist. Bezeichnet a den Winkel, den diese Projektion mit der X-Achse einschliesst, so sind die Koordinaten C1 und C2 des Vektors 𝕮 dargestellt durch
 |
Die Knotenlinie ☊ ☋ steht senkrecht auf der erwähnten Projektion des Vektors 𝕮 und ihr gegen den aufsteigenden Knoten ☊ gerichtete Halbstrahl O☊ schliesst mit der X-Achse den Winkel
 |
ein. Es ist deshalb
 |
Setzt man dies in die vorstehenden Gleichungen ein, so wird
| (115) |
 |
|
| (116) |
 |
Legt man durch den Durchstosspunkt I des Vektors 𝕯 mit der Himmelssphäre und durch die Durchstosspunkte N1, N2, N3 der Achsen X, Y, Z mit der Himmelssphäre die grössten Kreise N1I, N2I, N3I, dann erscheinen die Koordinaten D1, D2, D3 des Vektors 𝕯 durch die nachstehenden Ausdrücke veranschaulicht:
 |
Durch die Anwendung der bekannten Formel der sphärischen Trigonometrie
cos c = cos a cos b + sin a sin b cos C
folgt aus dem sphärischen Dreieck N1I☊, in dem der sphärische Winkel bei ☊ gleich dem Supplement von i ist,
cos N1I = cos Ω cos ω - sin Ω sin ω cos i
Aus dem sphärischen Dreieck 𝕮N2I, in dem der Bogen 𝕮N3 gleich π ⁄ 2. und der sphärische Winkel bei 𝕮 gleich dem Komplement von Ω ist, folgt
cos N3I = sin ω sin i.
Es folgt aus den vorstehenden Gleichungen:
| (117) |
 |
Durch diese Gleichungen, durch (114), (115), (116), d. h.
| (118) |
 |
und durch die Gleichungen (73), (75), (109), (113) ist der Zusammenhang zwischen den vektoriellen Elementen und den elliptischen Elementen eindeutig gegeben.
Kapitel III
Die Störungsrechnung
§ 12. Das Mehrkörperproblem der Himmelsmechanik und seine allgemeinen Integrale.
§ 13. Die Differentialgleichungen der hetiozentrischen Bewegung der Planeten.
§ 14. Die vektoriellen Grundgleichungen der Störungsrechnung.
§ 15. Die Klammerausdrücke von Lagrange.
§ 16. Berechnung der Lagrange′schen Klammerausdrücke für die vektoriellen Elemente.
§ 17. Die Gleichungen der zeitlichen Aenderungen der vektoriellen Elemente.
§ 18. Periodische und säkulare Störungen; die Bedeutung dieser letzteren für die Ziele der nachstehenden Forschungen.
§ 19. Die Differentialgleichungen der säkularen Aenderungen der vektoriellen Elemente.
§ 20. Klassische Form der Differentialgleichungen der säkularen Aenderungen der astronomischen Elemente.
§ 21. Die Integration der Differentialgleichungen der säkularen Aenderungen der astronomischen Elemente.
§ 22. Einige Schlussfolgerungen aus den vorstehenden Integralen. Die vorstehend abgeleiteten Integrale gliedern sich in zwei scharf oneinander geschiedene Gruppen (279) und (284). Durch die erste dieser zwei Gruppen erscheinen die säkularen Aenderungen der Elemente h und l oder jene der Elemente e und Π veranschaulicht, während durch die zweite Gruppe die säkularen Aenderungen der Elemente p und q oder jene der Elemente i und Π dargestellt sind. Die Aenderungen der Elemente e und Π können also unabhängig von jenen der Elemente i und Ω berechnet werden und umgekehrt, Diese Integrale sind auf Grund der im § 19 gemachten vereinfachenden Annahmen (237) gewonnen worden, durch welche die zweiten Potenzen der kleinen Zahlen e und i als vernachläsigbar betrachtet wurden. Es ist bemerkenswert, dass man zu den Integralen (279) gekommen wäre, wenn man auch die erste Potenz von i vernachlässigt hätte. Eine solche vereinfachende Annahme ginge nach (238), (239) und (243) darauf hinaus, C1 = 0; C2 = 0; p = O; q = O zu setzen. Dadurch blieben aber die Gleichungen (241) und (247) unberührt. Auch die Gleichungen (254) würden sich nicht geändert haben und folglich auch die Gleichungen (256), (258) und (278) und die Integrale (279) dieser letzteren Gleichungen. Daraus folgt aber, dass man bei der Berechnung der säkularen Aenderungen der Exzentrizitäten e und der Längen Π der Perihele die Bahnebenen aller in Betracht gezogenen Planeten als in der Grundebene liegend betrachten kann, ohne dadurch das Endergebnis der Rechnung in Mitleidenschaft zu ziehen. Anders gesprochen: die Neigungen der Bahnebenen der Planeten üben keinen Einfluss auf die säkularen Aenderungen der Exzentrizitäten und der Perihele aus.
Aehnlich verhält es sich mit den Integralen (284). Zu denselben Integralen wäre man gekommen, wenn man auch die erste Potenz von e vernachlässigt hätte. Eine solche vereinfachende Annahme ginge nach (239) und (245) darauf hinaus, D1 = 0; D2 = 0; h = O; l = O zu setzen. Dadurch blieben die Gleichungen (240) und (246) unberührt. Auch die Gleichungen (255) würden sich nicht geändert haben und ebenso wenig die Gleichungen (257), (259) und (283) und die Integrale (284)dieser letzteren Gleichungen. Man kann deshalb bei der Berechnung der säkularen Aenderungen der Neigungen i und der Längen Ω der aufsteigenden Knoten die Bahnen aller in Betracht gezogenen Planten als kreisrund annehmen Anders gesprochen: die Exzentrizitäten der Planetenbahnen üben keinen Einfluss auf die säkularen Aenderungen der Bahnneigungen und der Knoten aus.
Bei der Berechnung der säkularen Aenderungen der ersten Gruppe von Elementen würde man nur denjenigen Teil des auf den Fall von n Planeten erweiterten Ausdruckes (253) der Störungsfunktion in Betracht zu ziehen haben, der die Elemente ph und qh nicht enthält, und bei der Berechnung der säkularen Aenderungen der zweiten Gruppe von Elementen nur denjenigen Teil, der die Elemente hk und lk nicht enthält, wodurch die Störungsfunktion in zwei besondere Teile getrennt erschiene, die den zwei Gruppen von Elementen zugeordnet wären.
Diese Erkenntnis kann bei der Besprechung der Integrale (278) und (284) vorteilhaft verwertet werden. Ziehen wir vorerst die Integrale (278) in Betracht und fassen einen beliebigen Planeten mk in′s Auge. Weil wir jetzt nur von diesem Planeten reden wollen, können wir in (278) den Index k als überflüssig weglassen. Dadurch erschienen die säku1aren Aenderungen der auf diesen Planet sich beziehenden Elemente h und f dargestellt durch:
| (289) |

|
oder entwickelt:
| (290) |

|
Es ist nach (242)
| (291) |

|
Setzt man in die vorstehende Gleichung die Ausdrücke (289) ein, so wird:
| (292) |

|
wobei in der Doppelsumme i immer verschieden von i sein soll.
Mit dieser Formel können die säkularen Aenderungen der Exzentrizität der in Betracht gezogenen Planetenbahn berechnet werden. Die in dieser Formel auftretende Doppelsumme würde ihren grösstmöglichen numerischen Wert erreichen, wenn jeder der darin vorkommenden Kosinuse den Wert eins und jenes Vorzeichen aufweisen würde, bei dem Ni, Nj positiv wäre, In einem solchen Falle wäre also

|
worin N1, N2, ... Nn mit positivem Vorzeichen zu nehmen sind. Es ist deshalb
| (293) |

|
Der grösstmögliche Wert, den die Exzentrizität der Bahn eines Planeten erreichen könnte, ist gleich der Summe der absoluten Werte der zugehörigen Koeffizienten Ni. Dadurch ist der Exzentrizität eines jeden Planeten eine numerisch angebbare obere Grenze gesetzt.
Es folgt aus (289) und (291)
| (294) |

|
Durch Division dieser Gleichungen erhält man die Formel:
| (295) |

|
mit der die säkularen Aenderungen der Perihellänge berechnet werden können. Auch hinsichtlich dieser Aenderungen kann aus den vorstehenden Gleichungen ein allgemeiner Schluss gezogen werden.
Weisen wir dem Index i einen bestimmten aus der Reihe 1, 2, 3,... n beliebig herausgegriffenen Wert j zu. Es ist
Durch Division dieser Gleichungen erhält man die Formel:

|
Multiplizieren wir diese Gleichung mit e und setzen rechts für e · sin Π bzw. für e · cos Π die Ausdrücke (294) ein. Durch Gruppierung der dadurch entstandenen Glieder der rechten Seite der obigen Gleichung erhält man dort, wo i verschieden von j ist,

|
und and der Stelle, wo i gleich j ist,

|
Es ist deshalb
| (296) |

|
Unter dem Summenzeichen sind für i alle ganze Zahlen von 0 bis 1 zu setzen mit Ausnahme der Zahl j. Diese Summe kann ihrem absoluten Werte nach nicht grösser werden als die Summe der absoluten Werte der darin enthaltenen Koeffizienten Ni. Tritt also der Fall ein, dass der absolute Wert des Koeffizienten Ni grösser ist als die Summe der absoluten Werte aller übrigen Koeffizienten Ni, dann kann die rechte Seite der Gleichung (296) nie Null werden, d. h, der Winkel
| (297) |

|
kann nie die Grösse eines rechten Winkels erreichen, sondern nur zwischen bestimmten Grenzwerten -π ⁄ 2 < -φ0 < φ < φ0 < +π ⁄ 2 schwanken können. Es ist deshalb

|
Wie ich vorstehend bewiesen habe, verlaufen die säkularen Aenderungen der Perihellänge Π gerade so, als ob die Ebenen der Bahnen der Planeten zusammenfallen würden; man kann also bei der Betrachtung der säkularen Aenderungen von Π diese Ebenen als in die Grundebene umgeklappt denken. In einem solchen Fall ist Π ein ebener Winkel, den der aus dem Mittelpunkt der Sonne, dem Ursprung unseres Koordinatensystems X-Y-Z, gegen das Perihel des in Betracht gezogenen Planeten gerichtete Halbstrahl OP mit der X-Achse dieses Koordinatensystems ein schliesst. Denken wir uns in der Ebene X-Y einen anderen Halbstrahl OS, der im Initialmoment t = 0 mit der X-Achse den Winkel βj gebildet hatte und der sich, durch O ständig hindurchgehend, mit der konstanten WInkelgeschwindigkeit gj in der X-Y-Ebene dreht. Der Winkel, den dieser Halbstrahl OS mit der X-Achse zur Zeit t einschliesst, ist offenbar gleich

|
Es folgt aus den vorstehepden Gleichungen

|
Der gegen das Perihel gerichtete Halbstrahl OP kann sich von dem Halbstrahl OS nie mehr entfernen als um die Winkelgrösse φ0. Weil sich der Halbstrahl OS in der Ebene X-Y mit konstanter Winkelgeschwindigkeit ständig dreht, wird er den Halbstrahl OP mitziehen und vorschieben, so dass dieser, ähnlich der mittleren Bewegung n des Planeten, eine mittlere Bewegung gj aufweisen wird. Eine solche mittlere Bewegung wird nur dann sicherlich stattfinden, wenn der absolute Wert eines der Koeffizienten N1, N2, ... Nn die Summe der absoluten Werte der übrigen Koeffizienten übersteigt.
Die säkularen Aenderungen der Elemente p und q oder der Elemente i und Ω sind im vorliegenden Falle, wo wir einen bestimmten Planet in Betracht ziehen, wegen (284) durch die Ausdrücke nachstehender Form veranschaulicht:
| (298) |

|
Weil im vorliegenden Falle wegen (287) g1 = O ist, können die obigen Ausdrücke wie folgt geschrieben werden:
| (299) |

|
Es ist nach (243)
| (300) |

|
d. h.

|
Setzt man in die vorstehende Formel die Ausdrücke (298) ein, dann wird
| (301) |

|
wobei in der Doppelsumme i verschieden von j sein soll.
Diese Formel dient zur Berechnung der säkularen Aenderungen der Neigung i der Bahnebene des in Betracht gezogenen Planeten.
Auf dieselbe Weise wie vorstehend gezeigt worden ist, dass die Exzentrizität e einen angebbaren Grösstwert nie übersteigen kann, ergibt es sich auch hier
| (302) |

|
Es folgt aus den Gleichungen (298) und (300)
| (303) |

|
Durch Division dieser Gleichungen erhält man die Formel
Es folgt aus den Gleichungen (298) und (300)
| (304) |

|
mit der die säkularen 1:enderungen der Länge Ω des aufsteigenden Knotens berechnet werden können.
Auf dieselbe Weise, wie mittels (294) und (295) für Π, kann auch hier bewiesen werden, dass falls der absolute Wert eines der Koeffizienten Ni grösser ist als die Summe der absoten Werte aller übrigen Koeffizienten Ni, der aufsteigende Knoten eine mittlere Bewegung besitzt.
Ausgehend von den Gleichungen (189) und (190) können die säkularen Aenderungen des Elementes τ oder vermittels (113) jene der mittleren Länge ε der Epoche berechnet werden, Diese, übrigens sehr kleine Aenderungen kommen für die Ziele dieses Werkes gar nicht in Betracht, weshalb ich mich mit ihnen nicht zu befassen brauche.
Ueber die bisher durchgeführten numerischen Ausrechnungen der säkularen Aenderungen der Elemente e, Π, Ω, i wird im vierten Abschnitt dieses Werkes ausführlich berichtet werden. Diese haben ergeben, dass die Exzentrizitäten der Bahnkurven in die Neigungen der Bahnebenen aller Hauptplaneten zwischen eng gezogenen numerisch angebbaren Grenzen schwanken. Dadurch erscheint im Verein mit der säkularen Unveränderlichkeit der grossen Halbachsen der Planetenbahnen die Stabilität unseres Planetensystems auf unermesslich lange Zeiträume sichergestellt.
Einschub

Π = Ω + ω Länge des Perihels
Einschub Ende
Zweiter Abschnitt
Die Drehbewegung der Erde
Kapitel IV
Ableitung der für das Studium der Drehbewegungen der Erde erforderlichen Sätze und Gleichungen
§ 23. Das tellurische Massenpunktsystem. Unsere Erde samt ihrer Hydrosphäre und Atmosphäre bildet ein materielles System, in welchem alle drei Agregatzustände der Materie vertreten sind, Denken wir uns dasselbe in beliebig viele derart kleine Elemente zerteilt, dass jedes, derselben als ein diskreter Massenpunkt aufgefasst werden könne, dann gelangen wir zur Vorstellung, des tellurisehen Massenpunktsystems, das den folgenden Gesetzen gehorchen wird. Alle Elemente desselben ziehen sich nach dem Newtonschen Gravitationsgesetz gegenseitig an und werden von den übrigen Mitgliedern unseres Planetensystems ebenfalls angezogen. Von diesen letzteren müssen in den nachfolgenden Untersuchungen nur die Sonne und der Erdmond in Betracht gezogen werden, die Sonne wegen ihrer Grösse, der Mond wegen seiner Nähe; die Wirkung der Planeten auf den Gang der hier zu besprechenden Erscheinungen ist verschwindend klein. Die Anziehung der Sonne bzw. des Mondes auf die Elemente des tellurischen Massenpunktsystems sind als äussere auf dieses System einwirkenden Kräfte zu betrachten, während die gegenseitigen Anziehungen der einzelnen Elemente dieses Systems als innere Kräfte des Systems aufgefasst werden müssen. Neben diesen inneren Gravitationskräften sind im System selbst noch andere Kräfte wirksam, so die Reibungswiderstände als auch verschiedene Spannungen und Molekularkräfte die dem eigentlichen Erdkörper die Eigenschaften eines festen Körpers, der Hydrosphäre die Eigenschaften der Flüssigkeit und der Atmosphäre die Eigentümlichkeiten des Gases verleihen. Welcher Natur diese inneren Kräfte des Systems auch sein mögen, gehorchen sie alle dem Newtonschen Prinzip der Wirkung und Gegenwirkung, nach dem die Kraft 𝔭ik mit der ein beliebiger Massenpunkt mk auf einen anderen mi wirkt, gleich und entgegengerichtet ist der Kraft 𝔭ki, mit der der Massenpunkt mi auf jenen mk einwirkt; diese beiden Kräfte wirken in derselben Geraden: der Verbindungslinie jener zwei Massenpunkte. Diese Gleichheit der Wirkung und Gegenwirkung ist durch die nachstehende Vektorgleichung zum Ausdruck gebracht:
| (1) | 𝔭ik + 𝔭ki = 0. |
Um anzugeben, dass die beiden Kräfte in derselben Geraden wirken, sei 𝕽i der Ortsvektor des Massenpunktes Mi und 𝕽k jener des Massenpunktes mk in bezug auf einen beliebigen Aufpunkt, dann ist die obige Forderung ausgedrückt durch die nachstehende Vektorgleichung:
| (2) | [𝕽i · 𝔭ik] + [𝕽k · 𝔭ki] = = 0. |
Aus den vorstehenden Gleichungen lässt sich eine Reihe wichtiger Sätze und Gleichungen ableiten, was im nachstehenden geschehen soll.
§ 24. Die Impulssätze. Sei mi ein beliebiger Massenpunkt des in Betracht gezogenen materiellen Systems und 𝔓i die Resultante aller aüsseren auf diesen Massenpunkt einwirkenden Kräfte. Die Resultante aller inneren auf mi einwirkenden Kräfte erscheint nach den im vorhergehenden Paragraphen festgelegten Bezeichnungen durch Σ 𝔭ik veranschaulicht, wobei die Summe über das ganze System zu erstrecken ist. Denkt man sich im Raume ein ruhendes Koordinatensystem X1 — Y1 — Z1 mit dem Ursprung O1 festgelegt und ist 𝕽i der Ortsvektor von mi bezüglich dieses Systems, so kann der Massenpunkt mi, wofern man auf ihn alle in Betracht kommenden inneren Kräfte einwirken lässt, als freibeweglich betrachtet werden und es besteht deshalb die Gleichung:
| (3) |
 |
worin t die Zeit bedeutet.
Solche Bewegungsgleichungen lassen sich für alle Massenpunkte des Systems, deren Anzahl n sein möge, aufstellen, d. h. man kann dem Index i die Werte 1, 2,... n zuweisen, Es gelten also folgende n Gleichungen:
| (4) |
 |
Bildet man die Summe aller n Gleichungen (4), so wird rechtsstehend in der Doppelsumme
jede Kombination der Indices i und k zweimal vertreten sein: durch das Glied 𝔭ik und das Glied 𝔭ni. Nachdem sich aber diese paarweise auftretenden Glieder wegen (441) gegenseitig tilgen, so gelangt man zur folgenden Gleichung:
| (5) |
 |
Multipliziert man die Gleichungen (4) der Reihe nach vektoriell mit 𝕽1, 𝕽2, ... 𝕽n, und bildet die Summe der so erhaltenen Gleichungen, so wird man, nachdem sich, ähnlich wie früher, die paarweise auftretenden Glieder [𝕽i𝖕ik] und [𝕽ik𝖕ki] wegen (2) gegenseitig tilgen, zur folgenden Gleichung gelangen:
| (6) |
 |
Es stellt
| (7) |
 |
die Resultante aller auf das in Betracht gezogene materielle System einwirkenden äusseren Kräfte und
Es stellt
| (8) |
 |
das Drehmoment dieser Kräfte in bezug auf O1 dar. Man hat also:
| (9) |
 |
| (10) |
 |
Es stellt
| (11) |
 |
den Geschwindigkeitsvektor des Massenpunktes mi im ruhenden Koordinatensystem dar, so dass
| (12) |
 |
ist. Es ist ferner
so dass man statt (9) und (10) folgende zwei Gleichungen erhält
| (13) |
 |
| (14) |
 |
Diese zwei Gleichungen drücken die sogenannten Impulssätze aus. Es stellt nämlich Σmi𝖁i den Gesamtimpuls oder die Quantität der Bewegung des in Betracht gezogenen materiellen Systems dar, welche Benennungen man auch durch "Trieb" zu ersetzen pflegt. Der Ausdruck Σmi[𝕽i𝖁i] stellt die Summe der Momente der Quantitäten der Bewegung der einzelnen Massenpunkte bezüglich des Aufpunktes O1 dar; diese Benennung lässt sich durch die kürzere "Drehimpuls" oder, wenn das System ein fester Körper ist, durch "Schwung" ersetzen. Es besagt also die Gleichung (13), dass die zeitliche Aenderung des Triebs gleich ist der Resultante der äusseren Kräfte, während die Gleichung (14) besagt, dass die zeitliche Aenderung des Drehimpulses gleich ist dem Drehmoment der äusseren Kräfte in bezug auf den ruhenden Aufpunkt O1.
§ 25. Der Schwerpunktsatz. Ist S der Schwerpunkt, richtiger gesagt der Massenmittelpunkt des in Betracht gezogenen materiellen Systems und 𝕾 der Ortsvektor von S, so ist
| (15) |
 |
worin
| (16) |
 |
die Gesamtmasse des Systems bedeutet. Zweimalige Differentiation von (15) nach der Zeit t ergibt
d. h. wegen (9)
| (17) |
 |
Diese differentielle Bewegungsgleichung des Schwerpunktes S ist identisch mit jener eines freibeweglichen Massenpunktes von der Masse M, welcher dem alleinigen Einffuss der durch (7) gegebenen Resultante 𝕶 aller äusseren Kräfte unerworfen wäre, Es folgt daraus:
Der Schwerpunkt des Massenpunktsystems bewegt sich so, als ob alle Massen und alle äusseren Kräfte in demselben vereinigt wären. Die inneren Kräfte üben keinen Einfluss auf die Bewegung des Schwerpunktes aus.
§ 26. Unabhängigkeit der Drehbewegung von der fortschreitenden Bewegung. Man nehme vorläufig an, dass das in Betracht gezogene materielle System ein starrer Körper sei und frage nach der Bewegung dieses Körpers um seinen Schwerpunkt S. Zur Beantwortung dieser Frage verlege man den Ursprung O1 des bisher als ruhend im Raume angenommenen Koordinatensystems X1 — Y1 — Z1 in den Schwerpunkt S und bezeichne dieses neue translatorisch im Raume, also ohne Drehung sich bewegende Koordinatensystem mit X — Y — Z und seinen mit dem Schwerpunkt S zusammenfallenden Ursprung mit O. Die Ortsvektoren der Massenpunkte m1,m2, ... mn bezüglich O seien mit 𝖗1, 𝖗2, ... 𝖗n bezeichnet. Es ist dann
| (18) | 𝕽i = 𝕽 + 𝖗i i = 1, 2, ... n |
und zufolge von (15) und (16)
d. h.
| (19) |
 |
woraus wieder folgt
| (20) |
 |
Setzt man (18) in (10) ein, so wird
d. h.
und wegen (17), (19) und (20)
| (21) |
 |
Das Moment der äusseren Kräfte 𝕻i in bezug auf den Schwerpunkt S, d. h. in bezug auf den beweglichen Aufpunkt O ist dargestellt durch:
d. h. wegen (8) und (7)
| (22) |
 |
Es folgt also aus (21) und (22)
| (23) |
 |
Die Bewegung des starren Körpers um seinen Schwerpunkt hat drei Freiheitsgrade und ist durch die obige Vektorgleichung, welche dreien skalaren Gleichungen äquivalent ist, eindeutig gegeben. Diese Vektorgleichung ist von derselben Form wie die Gleichung (lO), wo der Aufpunkt O1, im Raume unbeweglich angenommen wurde, und besagt, dass sich der in Betracht gezogene starre Körper um seinen Schwerpunkt so drehe, als ob dieser letztere unbeweglich wäre. Diese Bewegung hängt nur von dem Drehmoment 𝕸 der äusseren Kräfte und nicht von deren Resultante 𝕶 ab.
Die Gleichungen (17) und (23) drücken, zusammengenommen, den Satz von der Unabhängigkeit der Translations- und der Rotationsbewegung aus. Nach (17) reduziert sich das Problem der Bewegung des Schwerpunktes eines freibeweglichen starren Körpers auf das Problem der Bewegung eines freien Massenpunktes, nach (23) reduziert sich das Problem der Drehung dieses Körpers um einen unbeweglichen Punkt. Wir haben deshalb im ersten Abschnitt dieses Buches bei der Beschreibung der Bewegung des Schwerpunktes der Erde oder jenes eines beliebigen Planeten nicht deren Bewegungen um ihre Schwerpunkte in Betracht ziehen müssen, und werden jetzt, wo es sich um die Beschreibung der Bewegung der Erde um ihren Schwerpunkt handelt, nicht die fortschreitende Bewegung desselben berücksichtigen müssen.
Die Gleichungen (17) und (23) gelten nicht nur für den Fall eines starren Körpers, sondern auch für den allgemeineren Fall eines beliebigen materiellen Systems, das den Voraussetzungen des § 23 genügeleistet, nur ist in diesem Falle, wenn das System mehr als sechs Freiheitsgrade besitzt, durch jene zwei Vektorgleichungen die Bewegung des Systems nicht gegeben.
§ 27. Einführung beweglicher Bezugssysteme. Auf dieselbe Weise, auf welche aus (10) die Gleichung (14) abgeleitet worden ist, folgt aus (23)
| (24) |
 |
worin 𝖛i die Geschwindigkeit des Massenpunktes mi im Bezugssystem X—Y&mdasch;Z bedeutet, welches wir das "ruhende" nennen wollen, weil in demselben alles so vor sich geht als ob es tatsächlich ruhend wäre. Aus diesem Grunde wollen wir die Bewegungen und die Geschwindigkeiten in diesem Bezugssystem kurz die "absoluten" benennen.
Der Vektor
| (25) |
 |
stellt also den absoluten Drehimpuls des in Betracht gezogenen materiellen Systems bezüglich O dar, so dass es ist:
| (26) |
 |
Es ist oft von Vorteil, ja sogar notwendig, den Betrachtungen ein Bezugssystem x—y—z zu Grunde zu legen, welches gegen das ruhende Drehbewegungen ausführt. Man nehme dabei an, dass der Ursprung des beweglichen Koordinatensystems x—y—z mit dem Ursprung O des ruhenden Systems X—Z zusammenfalle und dass jenes bewegliche System im betrachteten Augenblicke t gegen das ruhende eine Drehbewegung ausführe, die wegen obiger Voraussetzung nur um eine durch O hindurchgehende instantane Drehungsachse erfogen kann.

Diese Drehbewegung sei durch den Vektor 𝖜 veranschaulicht, d. h. dieser Vektor falle in die instantane Drehachse des beweglichen Systems, sei nach jener Seite dieser Achse gerichtet, von welcher aus gesehen die Drehung im positiven Sinn, d. h. entgegengesetzt dem Uhrzeiger erfolgt, und der Modul w des Vektors m sei gleich der augenblicklichen Winkelgeschwindigkeit der Drehbewegung.
Seien 𝖎, 𝖏, 𝖐 die in die Achsenrichtungen x, y, z fallenden Einheitsvektoren, so werden die Endpunkte dieser Vektoren infolge der Drehung des beweglichen Systems im Zeitpunkte t Geschwindigkeiten aufweisen, die, wie aus Fig. 6 ersichtlich, dargestellt sind durch
| (27) |
 |
Bildet man das skalare Vektorprodukt (𝕲𝖎), so ist nach der bekannten Regel für die Differentiation eines solchen Produktes
d. h. wegen der vorstehenden Gleichung
| (28) |
 |
Multipliziert man die Gleichung (26) skalar mit i, so bekommt man mit Benützung der vorstehenden Gleichung
| (29) |
 |
Zwei weitere Gleichungen von derselben Art werden erhalten, wenn man 𝖎 durch 𝖏, bzw. 𝖐 ersetzt.
Bezeichnet man die Koordinaten des Vektors 𝕲 in bezug auf das bewegliche System mit G1, G2, G3, jene des Vektors 𝖜 mit w1, w2, w3, und jene des Vektors 𝕸 mit M1, M2, M3, so ist
| (30) |
 |
|
| (31) |
 |
|
| (32) |
 |
§ 28. Das mit dem bewegten Körper fest verbundene Bezugssystem. Ist das in Betracht gezogene materielle System ein starrer Körper, so wird man das soeben benutzte bewegliche Koordinatensystem x—y— z vorteilhaft mit dem Körper selbst fest verbinden. In diesem Falle bedeutet 𝖜 auch die instantane Drehgeschwindigkeit des starren Körpers in bezug auf das ruhende Bezugssystem, so dass die absolute Geschwindigkeit 𝖛i des Massenpunktes mi durch den Ausdruck
| (34) |
 |
dargestellt erscheint. Es ist deshalb der durch (25) gegebene Drehimpulsvektor 𝕲 gleich
| (35) |
 |
Im vorliegenden Falle, wo die Massenverteilung eine kontinuierliche ist, wird die obige Summe durch ein Integral zu ersetzen sein, so dass es wird:
| (36) |
 |
wobei das Integral über die Gesamtmasse des bewegten Körpers zu erstrecken ist.
Es ist nach einem bekannten Satze der Vektorrechnung
| [𝖆[𝖇𝖈]] = 𝖇(𝖈𝖆) - 𝖈(𝖆𝖇) |
so dass man bekommt:
| (37) |
 |
Bezeichnet man die Koordinaten des Ortsvektors 𝖗 im beweglichen System mit x, y, z, so ist
| 𝖗 = x𝖎 + y𝖏 = z𝖐 | ||
| (𝖗𝖗) = x2; + y2; + z2 | ||
| (𝖜𝖗) = 𝖜1x + 𝖜2y + 𝖜3z |
Setzt man diese Ausdrücke in die Vektorgleichung (37) ein, so zerfällt dieselbe mit Rücksicht auf (30) in folgende drei skalare Gleichungen:
| (38) |
 |
1st das Bezugssystem x—y—z mit dem bewegten. Körper derart verbunden, dass die Koordinatenachsen mit den Trägheitshauptachsen, oder vielmehr, weil der Ursprung des Koordinatensystems x—y—z im Schwerpunkt des hewegten Körpers gelegen ist, mit den Zentralhauptachsen des bewegten Körpers zusammenfallen, so wird offenbar
| (39) |
 |
weil in diesem Falle die Deviationsmomente des Körpers Null werden. Die Ausdrücke
| (40) |
 |
stellen dagegen die Trägheitshauptmomente des bewegten Körpers dar. Es wird also
| (41) | G1 = Aw1; G2 = Bw2; G3 = Cw3 |
Diese Werte, in die Gleichungen (33) eingesetzt, ergeben:
| (42) |
 |
§ 29. Die Eulerschen Winkel. Denkt man sich um den gemeinsamen Ursprung O (Fig. 7) des ruhenden und des beweglichen Koordinatensystems eine Kugelfläche beschrieben, so durchdringen die positiven Aeste der Koordinatenachsen dieser beiden Systeme die Kugelfläche in den Punkten X, Y, Z bzw. x, y, z, die als Eckpunkte zwei sphärische Dreiecke XYZ und xyz begrenzen, deren Seiten und Winkel je 90° messen. Die Koordinatenebenen X—Y und x—y schneiden sich gegenseitig längs einer durch O gehenden Geraden OΩ, die die Knotenlinie genannt wird. Jener Durchstosspunkt O dieser Geraden mit der erwähnten Kugelfläche, der der Bedingung genügt, dass man auf der positiven Umlaufsrichtung xy nach der positiven Seite (d. h. nach der Seite des positiven Z) der Ebene X—Y gelangt, wird der aufsteigende Knoten genannt und die Richtung OΩ als die positive Richtung der Knotenlinie betrachtet. Die durch OZ und Oz gelegte Ebene, die der besseren Anschaulichkeit halber zur Bildebene der Figur gewählt wurde, steht auf der Knotenlinie senkrecht. Der Winkel Ψ, den die Knotenlinie mit der X-Achse einschliesst, wird der Präzessionswinkel, der anschliessende Winkel Φ, den die x-Achse mit der Knotenlinie bildet, der Rotationswinkel genannt, während der zwischen Z und z eingeschlossene Winkel Θ den Namen Nutationswinkel führt. Dies sind die drei Eulerschen Winkel, durch welche die Lage des beweglichen Koordinatensystems im ruhenden festgelegt werden kann.

§ 30. Polhodie und Herpolhodie. Bezeichnet man, wie bisher, die in die Richtungen der Achsen x, y, z des beweglichen Koordinatensystems fallenden Einheitsvektoren mit 𝖎, 𝖏, 𝖐 und die in die Richtungen der Achsen X, Y, Z des ruhenden Koordinatensystems fallenden Einheitsvektoren mit 𝖓1, 𝖓2, 𝖓3, so ist die Lage des Rotationsvektors 𝖜 im beweglichen System gegeben durch
| (43) | 𝖜 = w1𝖎 + w2𝖏 + w3𝖐 |
und im ruhenden durch
| (44) | 𝖜 = ω1𝖓1 + ω2𝖓2 + ω3𝖓3 |
worin w1, w2, w3 bzw. ω1, ω2, ω3 die Koordinaten des Vektors 𝖜 im beweglichen bzw. ruhenden System bedeuten. Die Eulerschen Winkel Ψ, Θ, Φ vermitteln den Zusammenhang der beiden Systeme und es sollen deshalb die Grössen w1, w2, w3 bzw. ω1, ω2, ω3 mittels dieser Winkel und ihren zeitlichen Ableitungen ausgedrückt werden. Zu diesem Zwecke ist folgendes zu berücksichtigen. Das sphärische Dreieck XYZ (Fig. 7) kann mit dem Dreieck xyz zur Deckung gebracht werden durch folgende drei Drehungen. Man drehe das Dreieck XYZ um OZ, also um 𝖓2 als Achse, um den Winkel Ψ, wodurch es in die Lage ΩKZ gelangt, man drehe weiter um die Knotenlinie OΩ, deren Einheitsvektor mit c0, bezeichnet werden möge, um den Winkel #920;, wodurch man zur Lage ΩRZ gelangt, man drehe schliesslich um Oz, also um 𝖐 als Achse, um den Winkel Φ wodurch man tatsächlich die Endlage xyz erreicht hat. Alle diese Drehungen sind im positiven Sinn, entgegengesetzt dem Sinne des Uhrzeigers, erfolgt. Bezeichnet man mit
 |
die zeitlichen Aenderungen der Eulerschen Winkel, so ist die aus solchen Aenderungen resultierende Rotationsgeschwindigkeit 𝖜 nach dem soeben mitgeteiltem dargestellt durch
| (45) |
 |
Bezeichnet man den in die Richtung OR fallenden Einheitsvektor mit 𝖍0, so folgt aus der Fig. 7
 |
d. h.
| (46) |
 |
Auf dieselbe Weise bekommt man, wenn man den in die Richtung OL fallenden Einheitsvektor mit 𝖌0 bezeichnet,
 |
d. h. wegen (45)
| (47) |
 |
Aus (43) und (46) folgt:
| (48) |
 |
Aus (44) und (47) folgt:
| (49) |
 |
Hat man die Eulerschen Winkel Ψ, Θ, Φ als Funktionen der Zeit t dargestellt, so stellen die Ausdrücke (48) und (49) für einen beliebig angenommenen Wert von t die Koordinaten eines und denselben Punktes dar: des Endpunkts P des Rotationsvektors 𝖜. Wird t als variabel angesehen, so stellen uns die obigen Ausdrücke zwei verschiedene Kurven dar. Durch (48) ist jene Kurve dargestellt, die der Endpunkt P des Rotationsvektors 𝖜 im Laufe der Zeit im beweglichen, also mit dem bewegten Körper fest verbundenen Bezugssystem beschreibt; diese Kurve wird die Polhodie genannt. Durch (49) ist dagegen jene Kurve dargestellt, die der Punkt P im ruhenden Bezugssystem, also im Raume beschreibt; diese Kurve wird die Herpolhodie genannt

Wird 𝖜 als Ortsvektor des Punktes P aufgefasst, so ist (46) die vektorielle Gleichung der Polhodie und (47) jene der Herpolhodie. Der Rotationsvektor 𝖜 beschreibt deshalb im Laufe der Zeit im bewegten Körper einen Kegel, dessen Spitze der Punkt O und dessen Leitkurve die Polhodie ist; dieser Kegel wird der Polhodiekegel genannt. Der Rotationsvektor 𝖜 beschreibt dagegen im Raume einen Kegel, dessen Spitze der Punkt O und dessen Leitkurve die Herpolhodie ist; dieser Kegel wird der Herpolhodiekegel genannt. Der Herpolhodiekegel ist im Raume unbeweglich, der Polhodiekegel im Körper unbeweglich, aber im Raume beweglich. In jedem Zeitpunkte haben diese beiden Kegel eine Erzeugende, den diesem Zeitpunkt entsprechenden Rotationsvektor 𝖜 gemeinsam, d. h. die diesem Zeitpunkt entsprechende instantane Rotationsachse. Um diese Achse führt der Körper und der mit ihm fest verbundene Polhodiekegel die instantane Drehbewegung aus, wodurch im nächsten Augenblicke die nächstliegende Erzeugende des Polhodiekegels zur Koinzidenz mit der nächstgelegenen Erzeugenden des Herpolhodiekegels gelangt. Daraus folgt, dass sich der Polhodiekegel und der Herpolhodiekegel in jedem Augenblicke längs ihrer gemeinsamen Erzeugenden gegenseitig berühren, mit anderen Worten: der Polhodiekegel rollt ohne zu gleiten auf dem Herpolhodiekegel. Es kann deshalb die Drehbewegung des in Betracht gezogenen Körpers auf folgende Weise beschrieben werden: Auf einem im Raume unbeweglichen Kegel K1 (Herpolhodiekegel) rollt ohne zu gleiten ein anderer Kegel K2 (Polhodiekegel), den damit fest verbundenen Körper mittragend. (Fig. 8).
§ 31. Einiges über das Gravitationsfeld raumfüllender Massen. Die Ergebnisse des ersten Abschnittes dieses Buches sind aus der Voraussetzung abgelleitet worden, die Mitglieder unseres Planetensystems ziehen sich gegenseitig derart an, als ob die Masse eines jeden derselben in seinem Massenmittelpunkt konzentriert wäre. Jetzt ist es am Platze, die Berechtigung dieser Annahme, die die Himmelskörper als diskrete Massenpunkte auffasst, zu überprüfen. Nach dem Newtonschen Gravitationsgesetz zieht eine im Punkte M konzentrierte Masse m die in einem anderen beliebigen Punkte S des Raumes befindliche Masseneinheit mit einer Kraft an, die durch die Formel
| (50) |
 |
dargestellt ist. In derselben bedeutet f die Gravitationskonstante, 𝕴 den Ortsvektor des Punktes S in bezug auf den Punkt M, und l den Modul dieses Vektors. Durch die obige Formel ist das durch die punktförmige Masse m geschaffene Gravitationsfeld mathematisch dargestellt. Wir wollen nun die Frage stellen und beantworten, wie dieses Gravitationsfeld beschaffen sein wird, wenn wir die punktförmige Masse m durch eine raumfüllende Masse M ersetzt uns denken. Ziehen wir zu diesem Zwecke einen in der Fig. 9 durch K dargestellten Massenkörper beliebiger, aber endlicher Abmessungen in Betracht; hinsichtlich der Form dieses Körpers und binsichtlich der Verteilung der Materie in seinem Innern brauchen wir vorläufig keine besondere Voraussetzung machen. Legen wir in den Massenmittelpunkt dieses Körpers den Ursprung O eines orthogonalen Koordinatensystems x—y—z und orientieren wir dieses System derart, dass seine Achsen mit den Trägkeitshauptachsen des Körpers K zusammenfallen. Es ergibt sich dann folgendes.

Das den Punkt M umfassende unendlich kleine Massenelement dm des Körpers K ruft in dem ausserhalb des Körpers K befindlichen Punkte S, d. h. an den hier sich zu denkenden Masseneinheit eine gravitationelle Feldkraft 𝕱 hervor, die durch den Ausdruck
| (51) |
 |
dargestellt ist. Die von der Gesamtmasse M des Korpers K herrührende Feldkraft wird durch das Vektorintegral
| (52) |

|
veranschaulicht sein, wobei das Integral sich über die gesamte Masse M des Körpers K zu erstrecken hat.
Es ist, wie sofort ersichtlich,

|
so dass man statt (52) erhält:

|
Weil, ganz allgemein, eine beliebige, auch unendliche Summe der Gradienten von Skalaren gleich ist dem Gradient der Summe dieser Skalaren, so bekommt man:
| (53) |

|
Setzt man also:
| (54) |

|
so wird
| (55) | 𝕱 = grad U |
Dadurch erscheint die Feldkraft 𝕱 des in Betracht gezogenen Gravitationsfeldes als der Gradient einer skalaren Grösse U dargestellt, die man als die Kräftefunktion zu bezeichen pflegt.
Bezeichnet 𝕽 den Ortsvektor von S in bezug auf O und 𝖗 den Ortsvektor von M in bezug auf O, so ist
| (56) | 𝖑 = 𝕽 - 𝖗 |
d. h.
| 𝖑𝖑 = 𝕽𝕽 - 2 𝕽 𝖗 + 𝖗 𝖗 |
oder, wenn man den Modul von 𝕽 mit R, und den Modul von 𝖗 mit r bezeichnet,
| l2 = R2 - 2 𝕽 𝖗 + r2. |
Es folgt aus dieser Gleichung
| (57) |

|
Setzt man voraus, dass r < R, d. h. 𝕽𝖗 ≤ 𝕽𝖗 < R2 ist, entwickelt den obigen Ausdruck in eine Binomialreihe und begnügt sich mit den ersten Gliedern derselben, so wird
| (58) |

|
Setzt man dies in (54) ein, so bekommt man:
| (59) |

|
Das Integral

|
stellt die Gesamtmasse des Körpers K dar. Es ist ferner, weil der Aufpunkt O der Vektoren 𝖗 im Massenmittelpunkt des Körpers K gelegen ist,

|
Es ist also
| (60) |

|
Bezeichhet man mit x, y, z die Koordinaten des Punktes M, und mit X, Y, Z jene des Punktes S, so ist
| (61) |

|
worin 𝖎, 𝖏, 𝖐 die Einheitsvektoren der Achsenrichtungen des Koordinatensystems bedeute. Es ist also

|
Setzt man diese Ausdrücke in (60) ein, so werden die Glieder mit den Produkten xy, yz, zx verschwinden, weil die Koordinatenachsen, wie festgestellt, die Trägheitshauptachsen des Körpers K sind, also nach (39)

|
ist. Man bekommt auf diese Weise:

|
d. h.
| (62) |

|
Die Ausdrücke
| (63) |

|
stellen die Trägheitshauptmomente des Körpers K dar und es wird deshalb
| (64) |

|
Dieser Ausdruck stellt die Kräftefunktion U der Attraktion des Körpers K, der Gradient von U die Feldkraft 𝕱 des durch den Körper K geschaffenen Gravitationsfeldes dar.
Wenn
| (65) | A = B = C |
d. h. das Trägheitsellipsoid des Körpers K eine Kugel wäre, dann würde man statt (64) den Ausdruck
| (66) |

|
und statt (55) den Ausdruck
| (67) |

|
erhalten. In einem solchen Falle wäre, wie es der Vergleich mit (50) ergibt, das dem Körper K zugehörige Gravitationsfeld gleich dem, den eine im Punkte O konzentriert gedachte Masse M hervorrufen würde.
Die den Ausführungen des ersten Abschnittes dieses Buches zugrunde gelegte Voraussetzung, dass sich die Mitglieder unseres Planetensystems gegenseitig, derart anziehen, als ob ihre Massen je in ihren Massenmittelpunkten konzentriert wären, würde also vollständigt erfüllt erscheinen, wenn diese Himmelskörper kugelförmig wären und die Dichte ihrer Materie nur eine Funklion der Entfernung vom Mittelpunkte einer solchen Kugel wäre, weil in einem solchen Falle die zentralen Trägheitsellipsoide dieser Himmelskörper Kugeln wären.
Diese Voraussetzung ist wegen der Abplattung dieser Himmelskörper, von der noch die Rede sein wird, nicht erfüllt, doch ist der Einfluss dieser Abplattungen auf die fortschreitende Bewegung dieser Himmelkörper wegen der fünften Potenz von R in den drei letzten Gliedern des durch (61) dargeslellten Ausdruckes von U und wegen der geringen gegenseitigen Abweichungen der darin ebenfalls vorkommenden Grössen A, B, C ein ganz verschwindender, weshalb die oben erwähnte Voraussetzung als vollständig zulässig zu betrachten ist. Nur bei der Bewegung des Erdmondes um die Erde macht sich die Abplattung dieser beiden Himmelskörper in Form einer kleinen, berechenbaren Störung geltend.
Dem entgegen ist die Abplattung der Himmelskörper von fühlbarem Einfluss auf ihre Drehbewegung; ich werde sie bei der Untersuchung der Drehbewegung der Erde zu berücksichtigen haben.
§ 32. Drehbewegung flüssiger oder gasförmiger Himmelskörper. Einige Mitglieder unseres Planetensystems befinden sich im gasförmigen oder flüssigen Zustande. Dies gilt vor allem für die Sonne; auch die grossen äusseren Planeten sind als noch nicht erstarrt zu betrachten. Dies folgt, wie ich dies in meiner im Vorwort angeführten akademischen Abhandlung "Untersuchungen über die thermische Konstitution der Planetatmosphären" auseinandergesetzt habe, aus der geringen mittleren Dichte dieser PIaneten und aus der rechnerisch ermittelbaren grösstmöglichen Höhe einer aus Wasserdampf anzunehmenden Hülle derselben. Auch unsere Erde befand sich einst, bevor sie sich mit ihrer Kruste bedeckte, in einem derartigen astralen Zustande. Es ist deshalb vom Interesse, die Frage zu beantworten, wie die Drehbewegung solcher gasförmiger oder flüssiger Himmelskörper erfolgen könne.
Bei der Beantwortung der gestellten Frage soll von der Viskosität des Mediums abgesehen werden. Unter dieser Annahme gilt für jedes Teilchen eines solchen Mediums die bekannte Gleichung:
| (68) |

|
In derselben bedeutet 𝖛 den Geschwindigkeitsvektor, 𝕻 die auf die Massenneinheit einwirkende Kraft, ρ die Dichte, p den Druck und t die Zeit.
Ausser der obigen Grundgleichung gilt die Kontinuitätsgleichung:
| (69) |

|
und die charakteristische Gleichung. Diese letztere ist für idealle Gase durch die Zustandsgleichung:
| (70) | p · v = R0 · θ |
gegeben, worin v das Volumen der Masseneinheit, R0 die Gaskonstante und θ die absolut gemessene Temperatur bedeutet. Weil v = 1&nsbp;⁄ ρ ist, ist die obige Gleichung von der Form:
| (71) | F(p, ρ, θ) = 0. |
Für eine unzusammendrückbare Flüssigkeit hat man statt (69)
| (72) | div 𝖛 = 0 |
zu setzen, und statt (70) die Gleichung
| (73) |

|
worin k den Dilatationskoeffizient und ρ0 die Dichte bei der Temperatur u = 0 bedeutet.
Um grossen mathematischen Schwierigkeiten auszuweichen, wollen wir uns im nachstehenden mit speziellen Formen der charakteristischen Gleichung begnügen. Für isotherme Zustandsänderungen der Gase, d. h. bei konstanter Temperatur θ = θ0, hat man als charakteristische Gleichung:
| (74) | p = R0 θ0 ρ |
Für adiabatische Zustandsänderungen hat man als charakteristische die Gleichung:
| (75) |

|
worin c bzw. c′ die spezifische Wärme bei konstantem Volumen bzw. konstantem Druck bedeutet. Die beiden Gleichungen (74) und (75) sind von der Form:
| (76) | ρ = f(p) |
und es soll im nachstehenden vorausgesetzt werden, dass die charakteristische Gleichung zu dieser Form von Gleichungen gehört. Führt man also die skalare Funktion
| (77) |

|
in die Rechnungen ein, so wird nach dem analytischen Ausdruch des Gradienten

|
Zieht man überdies in Betracht, dass sich die Kraft 𝕻 als Gravitationskraft ebenfalls als Gradient einer skalaren Kräftefunktion U darstellen lässt, so bekommt man, wenn man
| (78) | U - V = Q |
setzt, statt (68) die Gleichung:
| (79) |

|
Wählt man in der Rotationsachse des Himmelskörpers einen fixen Aufpunkt O und bezeichnet 𝖗 den Ortsvektor {OM} des in Betracht gezogenen Teilchens, 𝖓 dagegen den Einheitsvektor der positiven Richtung der Rotationsachse, so ist
| (80) | 𝖛 = 𝖜[𝖓 𝖗]. |
Dabei ist 𝖓 ein unveränderlicher Vektor und 𝖛 eine von der Zeit unabhängige Funktion von 𝖗. Es ist deshalb
| (81) |

|
Wird aus M das Lot MS auf die Drehachse gefällt und der Vektor {SM} mit 𝕽 bezeichnet, so ist
| (82) |

|
Bezeichnet R den Modul des Vektors 𝕽 und frägt man nach dem Gradient des Skalars R, so ist zu berücksichtigen, dass die entsprechenden Aequiskalarflächen Kreiszylinder sind mit der Achse OS, dass der Gradient senkrecht zu diesen Flächen steht und den Modul ∂R ⁄ ∂R = 1 aufweist. Es ist also
| (83) |

|
d. h. wegen (79), (81), (82) und (83)
| (84) |

|
Multipliziert man diese Gleichung mit dem eine beliebige Verrückung darstellenden Vektor d𝖘, so wird
| (85) |

|
Es stellt ganz allgemein
| grad W d𝖘 = dW |
die der Verrückung d𝖘 entsprechende Aenderung d W dcs Skalars W und es ist deshalb
| (86) |

|
Hier steht links ein exaktes Differential, es muss also auch 𝖜2 R dR ein exaktes Differential sein, weshalb 𝖜 nur von R abhängig, d. h. eine Funktion von der Form
| (87) | 𝖜 = F(R) |
sein muss. Setzt man also
| (88) |

|
so wird nach (86)

|
woraus man durch Integration und mit Berücksichtigung von (78) bekommt:
| (89) | U - V + Φ(R) = const. |
Die Flächen gleichen Druckes, die Niveauflächen, werden erhalten, wenn man der Grösse V einen konstanten Wert zuweist. Diese Flächen sind also durch die Gleichung
| (90) | U + Φ(R) = C |
veranschaulicht.
Soll also der in Betracht gezogene Himmelskörper Rotationsbewegungen um eine im Raume unveränderliche Achse vollführen, so kann dies unter den gemachten Voraussetzungen nur dann geschehen, wenn die Winkelgeschwindigkeit 𝖜 der einzelnen Elementarringe nur eine Funktion des Halbmessers R dieser Ringe ist. Weil man also für ein gegebenes R dasselbe 𝖜 bekommt, so haben alle auf einer Zylinderfläche, deren Achse die Drehachse ist, befindlichen Teilchen dieselbe Rotationsgeschwindigkeit und die Drehbewegung erfolgt derart, dass jeder dieser Zylinderflächen ihre eigene Rotationsgeschwindigkeit zukommt und sie wie eine feste materielle Fläche um ihre Achse rotiert. Von aussen betrachtet, geschieht die Bewegung derart, dass jeder Breitekreis, die Schnittlinie der erwähnten Zylinderfläche mit der Oberfläche des Himmelskörpers, seine eigene Rotationsgeschwindigkeit aufweist. Eine solche Drehbewegung der Himmelskörper wird die zonale genannt.
§ 33. Drehbewegung mit ausgeglichenen Winkelgeschwindigkeiten.
§ 34. Gleichgewichtsbedingungen.
§ 35. Das Theorem von Clairaut. Von der Voraussetzung ausgehend, die Erde habe bei ihrer Erstarrung jene Form beibehalten, die der Gleichgewichtsfigur eines sich drehenden flüssigen Himmelskörper entspricht, hat Clairaut sein Theorem betreffend die Abplattung der Erde abgeleitet. Es ist notwendig, sich mit diesem Theorem bekannt zu machen. …
Kapitel V
Die tägliche Drehbewegung der Erde und ihre Folgen
§ 36. Mechanismus der kräftefreien Drehbewegung der Erde.
§ 37. Erfahrungstatsachen.
§ 38. Die tägliche Drehbewegung der Erde und ihr Spiegelbild.
§ 39. Sphärische Koordinaten. Um die gegenseitigen Bewegungen der beiden Bezugssysteme, Erde bzw. Himmelskugel, mathematisch zu beschreiben, müssen in diesen Bezugssystemen eindeutig definierte Koordinatensysteme festgelegt werden. Dies geschieht auf folgende Weise.

Sei M (Fig. 13) ein beliebiger Punkt der Erdoberfläche, gekennzeichnet durch seine geographischen Koordinaten, nämlich durch seine geographische Breite φ, positiv gezählt vom Aequator gegen Norden, und seine geographische Länge ξ, positiv gezählt von einem festgelegten Nullmeridian in der Richtung von West gegen Ost. Sieht man von geringfügigen, durch die Anziehung der Sonne und Mond hervorgerufenen zeitlichen Aenderungen ab, die an einer anderen Stelle dieses Werkes behandelt werden, so kann die Richtung der irdischen Schwerkraft an jedem Punkt der Erdoberfläche als eine bestimmte und unveränderliche betrachtet werden. Diese Richtung wird durch einen, mit einem Gewichte beschwerten, frei hängenden Faden veranschaulicht und wird die Vertikalrichtung genannt. Denkt man sich dieselbe nach oben und unten bis an die scheinbare Himmelskugel verlängert, so wird sie dieselbe in zwei entgegengesetzen Punkten treffen, von welchen das obere der Zenit, das untere (dem Beobachter unsichtbare) Z′ das Nadir genannt wird. Legt man durch den Beobachtungspunkt M eine Ebene senkrecht zur Vertikalrichtung, also eine horizontale Ebene, so wird dieselbe die scheinbare Himmelskugel in einem grössten Kreise schneiden, welcher der Horizont des Standpunktes genannt wird. Dieser sei durch den Kreis NWH′OH dargestellt. Dadurch hat man eine, mit dem Standpunkt des Beobachters fest verbundene Ebene fixiert, was aber zum Aufbau eines Koordinatensystems noch nicht ausreicht. Um das noch fehlende Orientierungselement zu erhalten, hat man zu berücksichtigen, dass sich, wie gezeigt, die Himmelskugel relativ zum Beobachter um eine Achse dreht, die, durch den Standpunkt M hindurchgehend, der Rotationsachse der Erde parallel ist. Sei MN diese Achse; sie treffe die Himmelskugel in den Punkten N und N′. Weil nun die Abmessungen der Erde gegenüber jenen der Himmelskugel verschwindend klein sind, so sind die Punkte N und N′ auch jene, in denen die Verlängerungen der eigentlichen Rotationsachse der Erde die Himmelskugel treffen. Aus demselben Grunde wird die durch den Mittelpunkt der Erde gelegte Ebene, die der Ebene des Horizontes parallel ist, die Himmelskugel ebenfalls im Kreis HWH′OH schneiden. Man kann demnach ohne weiters den bisher eingenommenen, auf der Erdoberfläche befindlichen (anthropozentrischen, Standpunkt mit dem geozentrischen vertauschen, d. h. annehmen, dass der Punkt M mit dem Mittelpunkt der Erde zusammenfalle. Die beiden Punkte N und N′, also die Durchstosspunkte der Erdachse mit der Himmelskugel, heissen die Weltpole; der auf der Seite des Nordpoles der Erde gelegene Punkt N wird gleichfalls der Nordpol, der andere, N′, der Südpol genannt. Der grösste Kreis AWA′OA der Himmelskugel, dessen Pole die beiden Weltpole sind, heisst der Himmelsäquator; seine Ebene steht senkrecht auf der Erdachse und fällt mit der Ebene des Erdäquators zusammen.
Die Ebene, die durch die Pole N, N′ und den Zenit Z gelegt wird, heisst Meridian- oder Mittagsebene; sie schneidet die Himmelssphäre in einem grössten Kreise HZ′H′ZH, welcher der Meridian- oder der Mittagskreis des Standortes genannt wird und sowohl auf dem Horizont als auf dem Aequator senkrecht steht, da er die Pole dieser grössten Kreise enthält. Der Meridian schneidet den Horizont in zwei Punkten, von denen der dem Nordpol nähere H der Nordpunkt, der gegenüberliegende, H′, der Südpunkt genannt wird. Die Gerade HH′ in der Ebene des Horizontes, die den Nordpunkt mit dem Südpunkte verbindet, heisst die Mittagslinie. Die Schnittpunkto O und W des Horizontes und des Aequators heissen Ost- bzw. Westpunkt, von denen der erstere auf jener Seite, des Meridianes liegt, auf der die Gestirne sich über den Horizont erheben, d. h aufgehen, der letztere auf der entgegengesetzten Seite, wo die Sterne untergehen. Die Meridianebene HZ′H′Z schneidet, weil sie durch die Rotationsachse der Erde und die Vertikalrichtung MZ des Standortes gelegt ist, die Erdoberfläche nach einer krummen Linie, dem Meridian des Standortes.
Durch die vorstehenden Ueberlegungen sind drei mit dem Erdkörper fest verbundene Ebenen fixiert, nämlich die Ebene des Horizontes, des Aequators und des Meridians, von denen die letztere auf den zwei anderen senkrecht steht. Mit Benützung derselben können folgende Koordinatensysteme und sphärische Koordinaten festgelegt werden.
Die durch Zenit und Nadir gelegten grössten Kreise der Himmelskugel stehen auf dem Horizonte senkrecht, weil jene zwei Punkte die Pole des Horizontes sind. Diese Kreise werden die Vertikal- oder Höhenkreise genannt; auch der Meridian gehört zu denselben. Der durch den Ost- und Westpunkt gelegte Vertikalkreis hat ebenfalls einen besonderen Namen, den des ersten Vertikals, erhalten. Legt man durch einen beliebigen Punkt der Himmelskugel, also etwa durch den Stern S, den Vertikalkreis ZSD, so wird der Bogen DS des Vertikalkreises zwischen Horizont und Stern die Höhe des Sternes genannt. Dieser Bogen, der mit h bezeichnet werden möge, misst den Winkel DMS, den die Richtung MS mit der Ebene des Horizontes einschliesst, und ist positiv zu zählen vom Horizont gegen Zenit, negativ gegen das Nadir. Der sphärische Winkel H′ZS, den der durch S gelegte Vertikalkreis mit dem Meridiane bildet, heisst das Azimut und hat den zwischen Meridian- und Vertikalkreis liegenden Bogen H′D des Horizontes zum Masse. Diese Grösse, die mit A bezeichnet werden möge, wird vom südlichen Teile des Meridians in der Richtung von Süd über West, von 0° bis 360° gezählt. Die Grössen h und A sind die beiden auf den Horizont sich beziehenden sphärischen Koordinaten. Statt der ersteren kann auch deren Komplement, die Zenitdistanz genannt, benützt werden. Es ist dies der zwischen Zenit und Stern liegende Bogen ZS des Vertikalkreises, und soll mit z bezeichnet werden Es ist also immer h + z = 90°.<
Die Höhe des sichtbaren Weltpoles N über dem Horizonte des Standortes, also der Bogen HN, wird die Polhöhe genannt. Dieselbe ist offenbar gleich dem Bogen A&prim3é;Z, den die Vertikalrichtung des Beobachtungsortes mit der Ebene des Aequators bildet, d. h. gleich der geographischen Breite φ des Standortes.
Auf dieselbe Weise, wie man die auf den Horizont sich beziehenden Koordinaten festgelegt hat, können die auf den Aequator sich beziehenden vereinbart werden. Legt man durch die Weltpole und den Stern S den grössten Kreis NSB, Deklinations- oder Stundenkreis genannt. so heisst sein zwischen dem Aequator und dem Stern S liegende Bogen BS die Deklination des Sternes S. Diese Grösse soll mit Ζ bezeichnet unä positiv vom Aequator gegen den Nordpol gezählt werden. Der sphärische Winkel ZNS zwischen Stundenkreis und Meridian heisst der Stundenwinkel des Sternes; er hat das zwischenliegende Stück A′B des Aequators zum Masse und wird, wie das Azimut, vom südlichen Teile des Meridians in der Richtung von Süd über West gezählt. Der Stundenwinkel soll mit t bezeichnet werden. Man pflegt den Stundenwinkel mit dem Zeitmasse zu messen, indem man 360° gleich 24 h, d. h. 15° gleich 1 h, 1° = 4 m, 1′ = 4 s setzt. Die Gründe für dieses Vorgehen werden bald ersichtlich werden. δ und t sind Jie beiden auf den Aequator sich beziehenden Koordinaten. Statt δ kann auch dessen Komplement, der Bogen NS des Deklinationskreises, Poldistanz genannt, benutzt werden.
Von den beiden soeben festgelegten, mit dem Erdkörper fest verbundenen Koordinatensystemen ist das erste vorwiegend der astronomischen Beobachtungspraxis, das zweite dem Mechanismus der täglichen Bewegung des Himmels angepasst. Um diese Bewegung mathematisch beschreiben zu können, ist ein weiteres Koordinatensystem erforderlich, das mit der Himmelskugel fest verbunden ist. Diese hat mit dem Erdkörper die Rotationsachse NN′ und die Aequatorebene AWA′O gemeinsam und ihre tägliche Bewegung relativ zur Erde besitzt nur einen Freiheitsgrad. Es genügt also ein einziger Parameter oder Koordinate, um die Lage der Himmelskugel relativ zur Erde in jedem Moment angeben zu können. Als eine solche Koordinate wählt man den Stundenwinkel eines Punktes, des Aequators der Himmelssphäre. Dies geschieht auf folgende Weise.
Die Erde bewegt sich relativ zur Sonne von West nach Ost in einer Bahn, deren Ebene durch den Schwerpunkt, d. h. durch den Mittelpunkt der Sonne hindurchgeht, weshalb die relative Bewegung der Sonne zur Erde ebenfalls in demselben Sinne erfolgen wird, in einer durch den Erdmittelpunkt hindurchgehenden Ebene. Der Schnitt dieser Ebene mit der Himmelskugel, also die Projektion der relativen Sonnenbahn aus dem Erdmittelpunkt auf die Himmelskugel, wird die Ekliptik genannt. Weil die Rotationsachse der Erde nicht senkrecht steht auf der Bahnebene der Erde, sondern mit der Normalen dieser Bahn einen Winkel ε einschliesst, wird die Ekliptik nicht mit dem Himmelsäquator zusammenfallen, vielmehr mit demselben ebenfalls den Winkel ε einschliessen, der die Schiefe der Ekliptik genannt wird. Gegenwärtig ist ε = 23° 27′.

Seien (Fig 14) N, N′ die Weltpole und AA′ der zugehörige Aequator der Himmelskugel, ε die Ekliptik und P, P′ die zugehörigen Pole derselben. Der zwischen den Achsen MN und MP eingeschlossene Winkel oder der Bogen NP als auch der sphärische Winkel A′Υ′B′ sind der Schiefe ε der Ekliptik gleich. Die Gerade ΥΥ′, längs welcher sich die Ebenen des Himmelsäquators und der Ekliptik schneiden, steht senkrecht zur Ebene des Winkels NMP und wird die Tag- und Nachtgleichen- oder die Aequinoktiallinie genannt. Diese Gerade trifft die Himmelskugel in zwei einander gegenüberliegenden Punkten Υ und Υ′, die man die Tag- und Nachtgleichen- oder Aequinoktialpunkte nennt. Ekliptik und Aequator halbieren sich gegenseitig als grösste Kreise; jener von den beiden Aequinoktialpunkten (Υ in der Fig. 14), den die Sonne durchschreitet, wenn sie sich aus der südlichen Hälfte der Himmelskugel in die nördliche erhebt, heisst der Frühlings- Tag- und Nachtgleichenpunkt, kurz der Frühlingspunkt oder das Frühlingsäquinoktium, der andere, Υ′, der Herbstpunkt.
Ist NAN′A′N der Meridian des Standortes des Beobachters, so stellt der sphärische Winkel A′NΥ den jeweiligen Stundenwinkel des Frühlingspunktes dar und es hat dieser Winkel den Bogen A′Υ des Aequators zum Masse. Durch diesen Stundenwinkel ist die jeweilige Lage der Himmelskugel zu den mit dem Erdkörper fest verbundenen Koordinatensystemen eindeutig gegeben und es wird dieser Stundenwinkel, im Zeitmass ausgedrückt, die Sternzeit genannt; wir werden sie mit θ bezeichnen.
Der Himmelsäquator und die Ekliplik sind, wenn man von deren säkularen Aenderungen, von denen später die Rede sein wird, absieht, oder diese durch Festlegung einer bestimmten Epoche eliminiert, feste Kreise der Himmelskugel und können zum Aufbau der mit der Himmelskugel fest verbundenen Koordinatensysteme benutzt werden. Der eine dieser Koordinatensysteme hat die Aequatorebene zur Grundebene und die Aequinoktiallinie zur Grundrichtung. Legt man demnach durch einen beliebigen Punkt der Himmelskugel oder einen Stern S den Deklinationskreis NSB hindurch, so wird der Bogen ΥB des Aequators die gerade Aufsteigung oder die Rektaszension des Sternes genannt; wir werden diese Grösse mit a bezeichnen. Sie wird vom Frühlingspunkte aus von West gegen Ost, also in einer der täglichen Bewegung des Himmels entgegengesetzten Richtung gezählt und ebenfalls mit dem Zeitmasse gemessen. Rektaszension (a = ΥB) und Deklination (δ = NBS) sind die Koordinaten des mit der Himmelskugel fest verbundenen Aequator-Koordinatensystems.
Es folgt aus der Fig. 14
| arc ΥB + arc BA′ = arc ΥA′. |
Nun stellt nach den soeben getroffemn Vereinbarungen der Bcgen ΥB die Rektaszension a, der Bogen A′B den Stundenwinkel t des Gestirnes S dar; nach dem der Bogen ΥA′ die Sternzeit θ veranschaulicht, so folgt die bemerkenswerte Beziehung:
| (199) | a + t = θ. |
Ein weiteres mit der Himmelskugel fest verbundenes Koordinatensystem erhält man, wenn man die Ekliptik zur Grundebene und die Aequinoktiallinie zur Grundrichtung wählt. Legt man durch den Stern S einen durch die Pole P und P′ der Ekliptik hindurchgehenden Kreis PSGP′, der offenbar auf der Ekliptik senkrecht steht, so wird derselbe, Breitekreis genannt, die Ekliptik im Punkte G treffen. Der zwischen der Ekliptik und dem Stern liegende Bogen GS dieses Kreises wird die Breite genannt, der Bogen ΥG der Ekliptik dagegen die Länge des Gestirnes. Die Breite soll mit β bezeichnet und positiv gegen den in der nördlichen Hälfte der Himmelskugel gelegen Ekliptikpol P gezählt werden; die Länge soll mit λ bezeichnet und vom Frühlingspunkte aus von 0° bis 360° von West gegen Ost, also in derselben Richtung wie die Rektaszension gezählt werden. Länge und Breite sind die auf die Ekliptik sich beziehenden sphärischen Koordinaten der Gestirne.
Es ist oft erforderlich von einem der aufgezählten vier Koordinatensysteme zu einem andern dieser Systeme überzugehen. Weil die beiden Systeme des Aequators eine Koordinate, die Deklination, gemeinsam haben, die zwei anderen Koordinaten, Stundenwinkel in dem einen, Rektaszension in dem andern Systeme, durch die einfache Beziehung (199) zusammenhängen, hat man sich nur mit folgenden zwei Aufgaben zu befassen: 1) Höhe h und Azimut A in Stundenwinkel t und Deklination δ zu verwandeln und umgekehrt; 2) Rektaszension a und Deklination δ in Länge ^λ und Breite β zu verwandeln und umgekehrt, Durch Lösung dieser zwei Aufgaben ist auch die Frage erledigt, wie man aus Höhe und Azimut Länge und Breite berechnet oder umgekehrt.

Zur Lösung der ersten dieser zwei Aufgaben bedient man sich des durch Zenit, Weltpol und Stern gekennzeichneten sphärischen Dreiecks der Himmelskugel, das oft auch das nautische Dreieck genannf wird. Wie dies aus Fig. 13 und den zugehörigen Erörterungen folgt, ist in diesem Dreieck, das in Fig. 15 wiedergeben ist, die Seite NZ gleich dem Komplement (90° - φ) der geographischen Breite φ des Standortes des Beobachters, die Seite NS gleich dem Komplement (90° - δ) der Deklination des Gestirnes, während die Seite ZS gleich ist der Zenitdistanz z oder dem Komplement (90° - h) der Höhe des Gestirnes. Der sphärische Winkel ZNS stellt den Stundenwinkel t und der Winkel SZN das Supplement (180° - A) des Azimutes des Gestirnes dar. Weil die Seite NZ dieses Dreiecks durch den Standort des Beobachters als gegeben zu betrachten ist, können zwei von den vier Grössen h, t, ^δ, A durch die übrigen zwei mit den Mitteln der sphärischen Trigonometrie ausgredrückt werden. Zwecks späterer Anwendung sollen hier folgende Gleichungen abgeleitet werden. Man hat nach dem Kosinussatze der sphärischen Trigonometrie
| cos ZS = cos NZ · cos NS + sin NZ · sin NS · cos ∠ZNS | ||
| cos NS = cos ZN · cos ZS + sin ZN · sin ZS · cos ∠NZS |
d. h.
| (200) | cos z = sin h = sin φ · sin δ + cos φ · cos δ · cos t | |
| (201) | sin δS = sin φ · sin h - cos φ · cos h · cos A. |

Zur Lösung der zweiten Aufgabe bedient man sich des durch Weltpol, Ekliptikpol und Stern gekennzeichneten sphärischen Dreicks der Himmelskugel, das auch das astronomische Dreieck genannt wird. Es folgt aus Fig. 14 und den zugehörigen Erörterungen, dass in diesem Dreieck die Seite NP gleich ist der Schiefe ε der Ekliptik, Seite PS gleich dem Komplement (90° + φ) der Breite, Seite NS gleich dem Komplenlement (90° - δ) der Deklination des Gestirnes; der sphärische Winkel NPS ist, weil MΥ (Fig. 16) senkrecht auf der Ebene NMP steht, gleich dem Komplement (90° - λ) der Länge des Gestirnes, während der sphärische Winkel PNS gleich ist (90° + a). Weil die Seite NP als gegeben zu betrachten ist, können zwei von den vier Grössen a, δ, λ, β durch die übrigen zwei ausgedrückt werden. Es folgt nach den Kosinussätze der sphärischen Trigonometrie
| cos NS = cos PS · cos PN + sin PS · sin PN · cos ∠NPS | ||
| cos PS = cos NP · cos NS + sin NP · sin NS · cos ∠PNS |
d. h.
| (202) | sin δ = sin δ · cos ε + cos β · sin ε · cos λ | |
| (203) | sin β = cos ε · sin δ - sin ε · cos δ · cos a. |
und nach dem Sinussatz

|
d. h.
| (204) | cos a · cos δ = cos β · cos λ |
Eine übersichtlichere Einführung in die sphärische Trigonometrie ist an anderer Stelle auf dieser Website zu finden.
§ 40. Die tägliche Bewegung des Himmels.
§ 41. Die Bewegung der Sonne am Himmel.
§ 42. Nebeneinflüsse.
Kapitel VI
Die Präzession der Erdachse
§ 43. Geschichtliches. K1audius Pto1emaios berichtet in seinem Handbuch, dass Hipparch durch Vergleichung von zu seiner Zeit genau beobachteten Mondfinsternissen mit solchen, die noch früher von Timocharis beobachtet worden waren zu dem Ergebnis gelangte, dass die Spika von dem Herbstnachtgleichenpunkt gegen die Richtung der Zeichen zu seiner Zeit 6°, zu Timocharis Zeit dagegen nahezu 8° entfernt stand. Aehnliche Verrückungen fand Hipparch auch bei anderen von Timocharis oder Aristyll beobachteteten und in die Vergleichung miteinbezogenen Fixsternen. Es ergab sich dabei, dass durch diese Verrückungen die Entfernung der Sterne von der Ekliptik, ihre Breite, nicht betroffen erschien. Daraus schloss Hipparch mit einem gewissen Vorbehalt, dass die Nachtgleichen in einem Jahre mindestens (1 ⁄ 100)° gegen die Richtung der Zeichen zurückgegangen sein müssten. Durch die obigen Aussagen des Ptolemaios ist, trotzdem die betreffenden beiden Schriften des Hipparch nicht erhalten geblieben sind, die Hauptleistung Hipparchs sichergestellt. Ob die Verrückung der Nachtgleichen chaldäischen oder anderen älteren Himmelsbeobachtern aufgefallen ist, konnte trotz allen Nachforschungen nicht festgestellt werden.
Ptolemaios widmete dieser Himmelserscheinung, die später den Namen der Präzession der Nachtgleichen erhielt, den grössten Teil des siebenten Buches seines Hauptwerkes, worin er eigene Beobachtungen anführt, die mit jenen von Timocharis, Aristyll und Hipparch verglichen, ihm zu dem, ohne Vorbehalt verkündeten Ergebnis führten, dass die Fixsternsphäre, ausser ihrer täglichen Rotation um die Weltpole, sich um eine durch die Pole der Ekliptik gehende Achse in der Richtung der Zeichen drehe, wodurch die Nachtgleichenpunkte in entgegengesetzter Richtung wandern und in hundert Jahren einen Grad oder 36″ pro Jahr zurücklegen. Diese Zahl hat, wie schon erwähnt, bereits Hipparch und zwar als eine untere Grenze angegeben, wodurch sich Pto1emaios die ungerechtfertigte Verdächtigung De1ambre′s und Tannery′s zuzog, dass sein Sternkatalog nicht aus Beobachtung, sondern aus jenem von Hipparch durch einfache Extrapolation gewonnen worden sei.
Durch Pto1emaios′ ausführliche, klare und wissenschaftliche Behandlung wurde die Präzession der Nachtgleichen zu einem wohlbegründeten Bestandteil der alten Astronomie, was zu weiteren Beobachtungen und Berechnung Anlass gab. A1bategnius verglich die von ihm um 879 ermittelten Sternpositionen mit dem Sternkatalog des Ptolemaios und berechnete daraus eine jährliche Verrückung der Aequinoktien von 55″. Nassir-Edin fand um 1260, dass diese Verrückung 51″ betrage, wodurch er dem tatsächlichen Werte von 50″25 schon sehr nahe kam.
Die alexandrische Schule machte für die Verschiebung der Aequinoktialpunkte die Fixsternsphäre verantwortlich. Als Kopernikus sein heliozentrisches System ausbaute und die Fixsternsphäre still stehen hiess, deutete er, ganz richtig, die Präzession als eine Folge der Orientierungsänderung der Erdachse, kombinierte aber diese säkulare Drehung der Erdachse unnötigerweise mit einer jährlichen.
Newton entdeckte durch sein Gravitationsgesetz den wahren Grund und den ganzen Mechanismus der Präzession, die dadurch einen weiteren schlagenden Beweis für die Nichtigkeit seiner Lehre lieferte. Nachdem Newton im III. Buch, 11. Abschnitt, seiner Prinzipien die Ungleichheiten der Mondbewegung erforschte und fand, dass der störende Körper, die Sonne, eine rückläufige Drehung der Knoten der Bahnebene des Mondes hervorrufe, bewies er im IV. Abschnitt des erwähnten Buches, dass die Abplattung der Erde, bei der man die äquatoriale Anschwellung als eine Anhäufung der Satelliten deuten könne, eine ähnliche Erscheinung zur Folge haben müsse, so dass die Knoten der Aequatorebene der Erde, die Aequinoktialpunkte, eine der täglichen Drehung der Erde entgegengesetzte Bewegung, eben die durch die Beobachtung gefundene, ausführen müssen, welche Bewegung dadurch ihre vollständige Erklärung gefunden hat.
Bei den vorstehenden Betrachtungen Newtons über die Ursache der Präzession hat man mit zwei gleichwertigen störenden Körpern, Sonne und Mond, zu tun, deren Wirkungen sich im säkularen Betrage der Präzession summieren, weil aber die Schnittlinie der Bahnebenen dieser zwei störenden Körper den bereits erwähnten Rücklauf vollführt, der zu einem vollständigen Umlauf rund 19 Jahre erfordert, so wird sich diese Bewegung als eine weitere, periodische Störung der Orientierung der Erdachse fühlbar machen müssen. Diese Störung konnte wegen ihrer Kleinheit aber erst durch Brad1ey′s Beobachtungen 1748, nachgewiesen werden. Die erste Theorie dieser Erscheinung, die den Namen der astronomischen Nutation der Erdachse erhielt und deren Vorhandensein schon aus den Newtonschen Prinzipien gefolgert werden konnte, lieferte D′A1embert.
§ 44. Das Drehmoment der auf die Erde einwirkenden äusseren Kräfte. Bei der Untersuchung des Mechanismus der Präzession ist es erforderlich, so wie es Newton bereits getan hat, die Abplattun g der Erde zu berücksichtigen, denn nur in diesem Falle weist die Kraft, mit der die Sonne oder der Mond die Erde anzieht, ein Drehmoment bezüglich des Massenmittelpunktes der Erde auf. Ziehen wir vorläufig nur einen dieser beiden störenden Hfmmelskörper in Betracht, dessen Masse m wir uns im Punkte S (Fig. 9, Seite 111) konzentriert denken. Im § 31 wurde gezeigt, dass ein Himmelskörper, also im vorliegenden Falle die Erde, deren Masse mit M und deren Trägheitshauptmomente mit A, B, C bezeichnet werden mögen, die im Punkte S befindliche Masseneinheit mit einer Kraft anzieht, die durch (55) gegeben ist wobei U durch den Ausdruck (64) dargestellt erscheint. Infolgedessen wird die Erde den störenden Himmelskörper m mit einer Kraft anziehen, die durch
| 𝕶 = m𝕱 = grad U |
veranschaulicht ist, wobei für U statt (64) der Ausdruck:
| (230) |
 |
zu setzen ist.
Dem Newton′schen Prinzip der Aktion und Reaktion zufolge wird der störende Himmelskörper m die Erde mit einer Kraft anziehen, die durch -𝕶 veranschaulicht ist; die Gerade, in der diese Kraft wirksam ist, geht durch den Punkt S (Fig. 9) hindurch. Das Drehmoment dieser Kraft bezüglich des Massenmittelpunktes O der Erde ist, weil der Ortsvektor von S in bezug auf O mit 𝕽 bezeichnet wurde, gleich:
| (231) |
 |
d. h.
| (232) |
 |
Setzt man also
| (233) |
 |
so wird:
| (234) |
 |
d. h.
| grad U = grad U0 + U2grad U1 + U1grad U2 |
Es ist deshalb

|
Nun ist

|
d. h. diese Vektoren sind kollinear dem Vektor 𝕽, und es ist deshalb

|
so dass man bekommt:
| (235) |

|
Die partiellen Ableitungen des Ausdruckes U2 nach X, Y, Z, d. h.

|
stellen die Koordinaten des Vektors grad U2 dar, während jene von 𝕽 durch X, Y, Z gegeben sind. Man hat also nach dem analytischen Ausdruck des vektoriellen Produktes:
p>

|
Die Koordinaten M1, M2,M3, des Vektors 𝕸, d. h. seine in die Richtungen der Koordinatenachsen fallenden Komponenten, sind also durch die Ausdrücke veranschaulicht:
| (236) |

|
Für die Erde ist, wie bereits erwähnt,
| (237) | B = A. |
Es ist also
| (238) |

|
§ 45. Bewegungsgleichungen. Permanente und periodische Störungsglieder. Setzt man in die vorstehenden Gleichungen (238) f#252;r m die Masse des störenden Himmeskörpers ein, und für X, Y, Z dessen geozentrische Koordinaten, so erhält man die Koordinaten M1, M2, M3 des auf den Erdkörper einwirkenden Drehvektors 𝕸.Bezeichnet also m die Masse der Sonne und X, Y, Z, R deren geozentrische Koordinaten, m1 die Masse des Mondes und x, y, z, r dessen geozentrische Koordinaten, so ist
| (239) |

|
Die Präzession der Erdachse erforschend, machen wir die Vorausetzung, dass der Erdkörper seine Form nicht ändert, die Trägheitshauptmomente A und C also als konstante Grössen zu betrachten sind. In diesem Falle gelten für die Drehbewegung der Erde die Eulerschen Gleichungen (42), in die nach (237) B = A zu setzen ist. Man bekommt also mit Berücksichtigung der vorstehenden Gleichungen:
| (240) |

|
Dies sind die differentialen Gleichungen der Drehbewegung der Erde unter dem Einflusse der Anziehung von Sonne und Mond.
Es folgt aus der letzten der drei Gleichungen:
| (241) | w3 = n, |
worin n eine Konstante bedeutet. Dies besagt, dass die Winkelgeschwindigkeit der Eigenrotation der Erde um ihre polare Trägheitshauptachse, d. h. um ihre Figurenachse durch Sonne und Mond nicht gestört wird.
Es folgt aus der letzten der Gleichungen (48):
| (242) |

|
Man kann durch Benützung der Gleichungen (48) auch die Grössen w1 und w2 durch die Eulerschen Winkel Θ, Ψ und Φ ausdrücken und da sich auch die Drehmomentkomponenten, ähnlich wie es vorstehend geschehen ist, als partielle Ableitungen von Skalaren durch diese Winkel darstellen lassen, bekommt man die erforderlichen Differentialgleichungen, deren Integration die Grössen Θ, Ψ, Φ als Funktionen der Zeit, also die Lösung des gestellten Problems liefert. Dabei ist folgendes zu berücksichtigen. In den Koordinaten X, Y, Z und x, y, z kommen alle Eigentümlichkeiten der Umlaufsbewegung der Erde um die Sonne und jener des Mondes um die Erde samt allen ihren Störungen und Ungleichheiten zum Vorschein. Eine strenge, alle diese Eigentümlichkeiten berücksichtigende Lösung des gestellten Problems führt auf besonders lange Entwicklungen, hat beispielsweise 0ppolzer nicht weniger als 202 Störungsglieder in Betracht gezogen. Indessen sind die meisten dieser Glieder selbst für astronomische Zwecke belanglos, für die Probleme der Geophysik kommen aber nur die wichtigsten dieser Glieder wirklich in Betracht. Man wird die Rolle und Bedeutung der einzelnen solcher Störungsglieder erkennen, wenn man von der Betrachtung des zeitlichen Vetlaufes des Drehmoments 𝕸 des störenden Körpers ausgeht. Dabei soll vorerst nur die Sonne in Betracht gezogen werden, weil das Drehmoment ihrer Anziehung auch alle Merkmale jener des Mondes deutlich erkennen lässt.
Weil A = B und die Erde ein Rotationskörper ist, hat die Drehung der Erde um ihre Figurenachse keinen Einfluss auf die Grösse des Drehmoments 𝕸. Man kann deshalb bei der Berechnung von 𝕸 des mit der Himmelskugel verbundenen Koordinatensystems des Aequators sich bedienen. Die x-Achse dieses Koordinatensystems ist gegen den Frühlingspunkt Υ (Fig. 14), die z-Achse gegen den nördlichen Weltpol N gerichtet. Der Ortsvektor 𝕽 der Sonne schliesst mit der x-Achse den Winkel (x, 𝕽) ein, der offenbar gleich ist der Länge λ der Sonne. Mit der z-Achse wird jener Vektor einen Winkel (z, 𝕽) einschiessen, welcher gleich ist der Poldistanz oder dem Komplement (90° - δ) der Deklination der Sonne. Der Winkel (y, 𝕽), den der Ortsvektor 𝕽 mit der y-Achse einschliesst, ergibt sich dann aus der allgemeinen Beziehung:

|
an hat also

|
Es ist nach (217)

|
d. h.

|
Die Koordinaten X, Y, Z der Sonne erscheinen also durch die folgenden Ausdrücke dargestellt:
| (243) |

|
Es folgt aus (238) und (243):
| (244) |

|
Um die zeitliche Veränderlichkeit und namentlich den jährlichen Gang der obigen Grössen zu verfolgen, muss auch R durch λ ausgedrückt werden. Es folgt aus den Gleichungen (4), (5) und (111) des ersten Abschnittes dieses Buches:

|
worin a die grosse Halbachse, e die Exzentrizität der Erdbahn, λh die heliozentrisehe Länge der Erde und Π die heliozentrische Länge des Perihels bedeutet. Mit Benützung der Gleichung (215) bekommt man

|
Der obige Ausdruck kann, weil e immer sehr klein bleibt, in eine Reihe entwickelt werden. Dabei kann man die Potenzen des Kosinus durch den Kosinus des vielfachen Winkels ausdrücken, so dass man eine Reihe nachstehender Form erhält:

|
In dieser Reihe sind die Grössen e und Π, wie im ersten Abschnitt dieses Buches gezeigt, säkular schwach veränderlich, so dass sie vorerst als konstant betrachtet werden können. Die Länge λ nimmt jährlich um 2π zu, so dass die trigonometrischen Glieder der obigen Reihe ganzjährige, halbjährige, dritteljährige usw. Perioden aufweisen. Es wird sich zeigen, dass die Wirkung der periodischen Glieder auf die Drehbewegung der Erde um so kleiner ausfällt je kleiner ihre Periode ist; weil überdies die Koeffizienten der obigen periodischen Glieder sehr klein sind und rasch abnehmen, so treten diese Glieder gegenüber den noch zu besprechenden periodischen Gliedern so zurück, dass man sie vorläufig ausser Acht lassen und setzen kann:
| (245) | R = a. |
Man bekommt dann statt (244):
| (246) |

|
Bezeichnet man also mit 𝖎1, 𝖎2, 𝖎3, die Einheitsvektoren der Richtungen x, y, z unseres Koordinatensystems und setzt zwecks kürzerer Schreibweise
| (247) |

|
so wird

|
Der Vektor 𝕸 kann also als die Summe zweier Vektoren 𝕸s und 𝕸p aufgefasst werden; es ist dabei
| (248) | 𝕸 = 𝕸s + 𝕸p |
| (249) |
 |
| (250) |
 |
Der Vektor 𝕸s ist gegen den Frühlingspunkt gerichtet und vom jährlichen Gange der Sonne unabhängig. Dieser Vektor liegt im benutzten Koordinatensystem unbeweglich und soll der permanente Bestandteil des Drehmoments 𝕸 genannt werden.
Der Vektor 𝕸p ist dagegen ein veränderlicher Vektor. Verlegt man seinen Anfangspunkt in den Ursprung des Koordinatensystems, so sind die Koordinaten seines Endpunktes L gegeben durch:
 |
Eliminiert man aus diesen zwei Gleichungen λ, so bekommt man
 |
ais die Gleichung der Bahnkurve des Endpunktes L des Vektors 𝕸p. Diese Kurve ist eine Ellipse und der Vektor 𝕸p ein periodisch sich ändernder Vektor; er soll der periodische Hauptbestandteil des Drehmoments genannt werden.
Der Voraussetzung (245) zufolge nimmt die Länge der Sonne mit der Zeit t gleichförmig zu. Zählt man die Zeit vom Durchgang der Sonne durch die x Achse, so wird:
| (251) |
 |
Die Komponenten M1′ und M2′ des Vektors 𝕸p unterliegen harmonischen Schwankungen mit einer halbjährigen Periode.
Hätte man bei der Ermittlung von λ als Funktion der Zeit t die Exzentrizität der Erdbahn berücksichtigt, so wären, wie am Beispiel von 1 ⁄ R gezeigt, weitere periodische Glieder zu Tage getreten, welche indessen aus bereits erwähnten Gründen von untergeordneter Bedeutung sind. Aus diesem Grunde sollen vorerst nur die oben abgeleiteten Hauptglieder 𝕸s und 𝕸p des Drehmoments in Betracht gezogen werden, zumal wir in denselben die typischen Vertreter beider Kategorien der Störungsglieder vor uns haben und ihre Eigentümlichkeiten auch für die übrigen Störungsglieder charakteristisch sind.
§ 46. Wirkung der einzelnen Bestandteile des Drehmoments. Die Ebene der Erdbahn kann, wenn man von ihren langsam vor sich gehenden Schwankungen, die später Berücksichtigung finden sollen, absieht, als im Raume unveränderlich betrachtet werden. Diese Ebene oder, besser gesagt, die Ebene der scheinbaren Sonnenbahn, der Ekliptik, soll zur X- Y-Ebene des sogleich zu benützenden ruhenden Koordinatensystems gewählt werden. Sei also (Fig. 7) O der Schwerpunkt der Erde und X- Y die unveränderlich vorausgesetzte Ebene der Ekliptik; die X-Achse des ruhenden Koordinatensystems sei dabei, aus Gründen, welche man bald kennen lernen wird, gegen den Herbstpunkt einer bestimmten Epoche gerichtet. Das mit der Erde fest verbundene, also das bewegliche Koordinatensystem sei das mit x-y-z bezeichnete; die Figurenachse der Erde sei zur z-Achse dieses Systems gewählt, die Schnittgerade des Erdäquators und des Greenwichers Meridianes zur x-Achse. Die x-y-Ebene des beweglichen Koordinatensystems schneide zur Zeit t die X-Y-Ebene des ruhenden Koordinatensystems längs der Geraden O☊; diese steht senkrecht auf der Ebene ZOz, welch letztere zur Bildebene der Figur gewählt wurde. Die in diese Bildebene fallende Gerade OR steht senkrecht auf der Geraden O☊. Der Punkt ☊ stellt den aufsteigenden Knoten des Himmelsäquators in bezug auf die Ekliptik dar, er ist also der absteigende Knoten der Ekliptik in bezug auf den Himmelsäquator; ☊ stellt also den jeweiligen Herbstpunkt dar. Bezeichnet also 𝖈0 den Einheitsvektor der Richtung O☊ und 𝖍0 den Einheitsvektor der Richtung O☊, so besteht zwischen diesen Vektoren und den vorstehend in (249) und (250) benutzten Einheitsvektoren der folgende Zusammenhang:
| (252) |
 |
Es ist deshalb:
| (253) |
 |
|
| (254) |
 |
Die Winkel XO☊, ☊Ox, ZOz stellen die drei Eulerschen Winkel Ψ, Φ, Θ dar, welche die Lage des beweglichen Systems in bezug auf das ruhende eindeutig festlegen. Hinsichtlich dieser Winkel ist folgendes zu bemerken. Der Winkel Θ stellt die Schiefe der Ekliptak zur Zeit t dar, es ist also
| (255) |
 |
Der Winkel Φ misst den Bcgen des Himmelsäquators, der zwischen dem Herbstpunkt und dem Greenwicher Meridian gelegen ist, ergänzt also die im Winkelmass gemessene Sternzeit Greenwich zu 180°.
Nach diesen Festlegungen kann zur Ermittlung der Drehbewegung der Erde unter dem Einflusse des Drehmoments 𝕸 geschritten werden. Dabei soll die im § 36 erwähnte freie Nutation der Erdachse ausser Acht gelassen werden. Weil, wie nachträglich beglaubigt werden wird, der Rotationsvektor 𝖜 sich unter dem Einflusse des Drehmoments 𝕸 nur unendlich wenig von der Figurenachse der Erde entfernen kann, so wird, ähnlich wie bei der Berechnung der Störungen erster Ordnung, von seiner Abweichung von der Figurenachse vorerst abgesehen und angenommen werden, dass der Drehvektor 𝖜 die Richtung der z-Achse aufweise. Es ist also:
 |
d. h. wegen (43) und (241)
 |
und wegen (41)
 |
d. h.
| (256) |
 |
Der Vektor 𝕲 ist ein im beweglichen Bezugssystem unveränderlicher Vektor mit einer skalaren Grösse G = nC. Man denke sich diese Grösse auf der z-Achse (Fig. 7, Seite 107) aufgetragen, d. h. OT = G3 gemacht und frage nach den Aenderungen des Vektors 𝕲 im ruhenden Bezugssystem. Seien dΦ, dΘ, dΨ die dem Zeitelement dt zugehörigen Aenderungen der Eulerschen Winkel. Weil 𝕲 mit der z-Achse zusammenfallend allgenommen wurde, so hat die Aenderung des Winkels Φ keinen Einfluss auf die Lage des Vektors 𝕲 im ruhenden Bezugssystem. Eine Zunahme des Winkels Θ um dΘ hat die Verschiebung OT · dΘ des Punktes T in der Ebene ZOz, senkrecht zu OT, also entgegengesetzt der Richtung des Einheitsvektors 𝖍0 zur Folge. Daraus resultiert eine Aenderung des Vektors 𝕲 um -G3dΘ · 𝖍0. Eine Zunahme des Winkels Ψ um dΨ hat eine Drehung der Ebene ZOz um die Achse Z, also eine Verschiebung G3 sinΘdΨ des Punktes T zur Folge und zwar senkrecht zu dieser Ebene in der Richtung des Einheitsvektors 𝖈0. Daraus resultiert aber eine Aenderung des Vektors 𝕲 um G3 sin Θ dΨ 𝖈0. Es ist also die Gesamtänderung des Vektors 𝕲 dargestellt durch:
 |
so dass man bekommt:
| (257) |
 |
Nach dem Impulssatze (26) muss der vorstehende Ausdruck gleich sein dem Drehmoment
 |
der äusseren Kräfte. Man hat also mit Rücksicht auf (253) und (254)
 |
Durch skalare Multiplikation mit 𝖈0 bzw. 𝖍0 kann die vorstehende Vektorgleichung in folgende zwei skalare Gleichungen getrennt werden:
| (258) |
 |
|
| (259) |
 |
Es wird sich zeigen, dass die Aenderungen von Θ so klein sind, dass sie im Gliede sin Θ nicht zum fühlbaren Ausdruck gelangen, weshalb man in (258) die durch Ms bzw. M1′ hervorgerufenen Aenderungen von Ψ getrennt berechnen kann. Auf diese Weise findet man, dass die Wirkung des permanenten Bestandteiles 𝕸s des Drehmoments 𝕸 durch die Gleichung:
| (260) |
 |
gegeben ist, während die Wirkungen des periodischen Bestandteiles 𝕸p des Drehmoments 𝕸 durch die Gleichungen
| (261) |
 |
wiedergegeben sind.
Es folgt aus (260), (249) und (255)
| (262) |
 |
Diese Gleichung besagt, dass der permanente Bestandteil des Drehmoments eine gieichförmige Abnahme des Winkels Ψ, also eine rückläufige Bewegung der Knotenlinie O☊ verursacht. Diese Bewegung hat keine Aenderung des Winkels Θ zur : Folge und es ist, wenn man nur den permanenten Anteil des Drehmoments berücksichtigt, Θ′ = 0. Daraus folgt aber aus der allgemeinen Gleichung (45), dass der Rotationsvektor 𝖜 durch:
| (263) |
 |
gegeben ist.
Es folgt aus der Fig. 7
 |
also
 |
d. h. wegen (242)
 |
Es ist ferner:
 |
also
| (264) |
 |
d. h. wegen (31), (41) und (237)
| (265) |
 |
Der Drehimpulsvektor 𝕲 ist also in aller Strenge nicht durch (256) dargestellt, weil er eine in die x-y-Ebene fallende Komponente
| (266) |
 |
aufweist und mit der z-Achse einen Winkel φ einschliesst, welcher gegeben ist durch:
| (267) |
 |
Aus den nachstehend mitgeteilten numerischen Angaben über die Drehbewegung der Erde wird man ersehen, dass der Beitrag (226) zum ursprünglich angenommen en Drehimpuls (256) und die durch (267) gegebene Abweichung seiner tatsächlichen Richtung von der angenommenen 𝖐 so verschwindend klein sind, dass sie das Endergebnis (262) der Berechnung nur unmerklich beeinflussen. Zu einer Berechnung der Störungen zweiter Ordnung, durch welche die obigen Abweichungen zu berücksichtigen wären, liegt also kein Anlass vor.
Dem Ausdruck (262) kann auch eine andere, für die späteren Anwendungen zweckmässigere Form gegebenen werden. Bedeutet T die Umlaufszeit der Erde um die Sonne, so ist nach der Gleichung (80) des ersten Abschnittes dieses Buches
| (268) |
 |
Bezeichnet also
| (269) |
 |
die mittlere Bewegung der Erde um die Sonne, so kann man auch setzen:
| (270) |
 |
Auf diese Weise bekommt man statt (262)
| (271) |
 |
Die Grösse:
| (272) |
 |
stellt den absoluten jährlichen Betrag der Solarpräzession dar.
Um die Wirkungen des periodischen Bestandteiles 𝕸p des Drehmoments der Sonnenanziehung zu ermitteln, hat man in (261) die Ausdrücke (251) einzusetzen. Es folgt mit Berücksichtigung von (247), (255), (269) und (270)
| (273) |
 |
|
| (274) |
 |
Integriert mah die vorstehenden Differentialgleichungen, wobei, wie bereits erwähnt, rechts die Veränderlichkeit von Θ nicht zu berücksichtigen ist, so folgt, wenn man die Zeit t von dem Augenblicke zählt, in welchem Ψ = 0 und Θ seinen Maximalwert erreicht,
| (275) |
 |
|
| (276) |
 |
d. h. wegen (272) und (269)
| (277) |
 |
|
| (278) |
 |
§ 47. Die Präzession der Erdachse. Aus dem vorstehenden folgt, dass der permanente Bestandteil des Drehmoments der Sonnenanziehung auf die Erde eine rückläufige Bewegung der Knoten des Himmelsäquators und der Ekliptik längs dieser letzteren zur Folge hat. Diese Bewegung, pro Zeiteinheit berechnet, ist nach (271) und (255) durch den Ausdruck gegeben:
| (279) |

|
Die Anziehung des Mondes hat eine ähnliche, und zwar wegen der Nähe dieses Himmelskörpers, quantitativ grössere Wirkung zur Folge, deren mathematischen Ausdruck man erhalten wird, wenn man in der vorstehenden Gleichung die Masse m der Sonne durch die Masse m, des Mondes, die mittlere Bewegung ν der Sonne um die Erde durch die mittlere Bewegung ν1 des Mondes um die Erde und die Schiefe der Ekliptik ε durch die Neigung ε2 der Mondbahn zur Ebene des Himmelsäquators ersetzt. Dabei ist folgendes zu berücksichtigen. Die Mondbahn schliesst mit der Ebene der Ekliptik einen nahezu unveränderlichen Winkel ε1 = 5%deg; 9′ ein, dabei dreht sich, wie dies noch ausführlich besprochen werden wird, die Ebene der Mondbahn infolge der Störung durch die Sonne derart, dass die Knoten der Mondbahn längst der Ekliptik rückl&228:ufig wandern, weshalb die Neigung der Ebene der Mondbahn zur Ebene des Himmelsäquators zwischen (ε - ε1) und (ε + ε1) schwankt. Nachder es sich oben um den permanenten Bestandteil des Drehmoments der Mondanziehung handelt, so werden wir vorläufig in (279) für ε2 den Mittelwert zwischen (ε - ε1) und (ε + ε1), also den Wert ε einsetzen, später aber eine schärfere Berücksichtigung aller soeben erwähnten Umstände nachholen. Auf diese Weise bekommt man für die stationäre Wirkung der Mondanziehung folgenden Ausdruck:
| (280) |

|
Dabei ist nach (269)
| (281) |

|
worin T die siderische Umlaufszeit der Erde um die Sonne und T1 die siderische Umlaufszeit des Mondes um die Erde bedeutet.
Die Gesamtwirkung der Sonne und des Mondes, die sogenannte lunisolare Präzession, ist also durch den nachstehenden Ausdruck gegeben:
| (282) |

|
Dabei wurde die Masse M der Erde gegen die Masse m der Sonne als ausserordentlich klein vernachlässigt.
Die Zeit, während welcher der Eulersche Rotationswinkel Φ der Erde um 2π zunimmt, wird der Sterntag genannt. Bezeichnet man diese Zeitspanne mit τ, so ist
| (283) |

|
Weil in (242), wie es sich gleich zeigen wird, Ψ′cos Θ vernachlässigbar gegen Φ′ ist, so kann gesetzt werden
| (284) |

|
Man bekommt also für den absoluten jährlichen Betrag der lunisolaren Präzesion den folgenden Ausdruck:
| (285) |

|
Der numerische Wert dieses Ausdruckes hängt von der schwach veränderlichen Grösse ε ab; setzt man darin für ε den bisher benutzten, der Gegenwart entsprechenden abgerundeten Wert ε = 23″27′ ein und berücksichtigt, dass
| T = 366,25 τ; T1 = 27,397 τ, m1 = 0,0123 M, (C - A) ⁄ C = 0,003261, |
ist, so bekommt man pτ = 50″36 als den jährlichen Betrag der Lunisolar-Präzession. Hievon entfällt auf die Anziehung der Sonne 15&Primen;88, auf jene des Mondes 34″48.
Zu dieser Berechnung ist folgendes zu bemerken. In Wirklichkeit wird der jährliche Betrag der Präzession nicht aus dem numerischen Wert der Grösse (C - A) ⁄ C berechnet, sondern, umgekehrt, aus dem durch direckte Beobachtung gewonnenen Betrag der Präzession die Grösse (C - A) ⁄ C ermittelt, was am obigen Zusammenhang nichts ändert. Nach den Berechnungen von Newcomb entspricht der Epoche 1850,0 und pro tropisches Jahr ein Betrag der Lunisolar-Präzession von 50″3684, so dass der hier errechnete Wert eine hinreichende Genauigkeit aufweist. Infolge dieser Verschiebung der Aeqinoktialpunkte würde jeder derselben während (360 · 60 · 60) ⁄ 50,36 = 25.735 Jahren, also während eines Zeitintervalles von rund 26.000 Jahren einen vollständigen Umlauf längs der Ekliptik vollführen.

Dieses Intervall wird mitunter auch das Platonische Jahr genannt. Infolge dieser Verrückung der Aequinoktialpunkte beschreiben die beiden Weltpole auf der Himmelssphäre um die beiden Pole der Ekliptik Kreisbahnen mit dem scheinbaren Radius gleich der Schiefe der Ekliptik. Die auf diese Weise ermittelte Bahn des nördlichen Weltpoles ist in Fig. 20 veranschaulicht. Diese Kreisbahn stellt den Schnitt des Herpolhodiekegels der Erddrehung mit der scheinbaren Himmelskugel dar.
Fragen wir nach der Gestalt des Polhodiekegels, d.h. nach der Kegelfläche, welche die Drehachse im Erdkörper selbst beschreibt! Die Gleichung der Polhodie ist duch (264) gegeben, worin 𝖜 als Ortsvektor aufzufassen ist und 𝖎, 𝖏, 𝖐 die Einheitsvektoren des mit dem Erdkörper fest verbundenen Koordinatensystems x—y—z bedeuten. Aus (264) folgt, dass die Polhodie ein Kreis ist, der in der Entfernung n vom Erdmittelpunkt die Figurenachse der Erde senkrecht umschlingt und einen Radius R aufweist, welcher gegeben ist durch:

|
woraus wieder folgt
| R = -Ψ′ sinΘ |
Der Oeffnungswinkel α des Polhodiekegels ist also gegeben durch
| (286) |

|
wobei man wegen der Kleinheit dieses Winkels dessen Tangens durch den Bogen ersetzt hat.
Man bekommt mit Benützung von (255), (282), (284) und (258)
| (287) |

|
d. h. mit den bereits angegebenen numerischen Werten für T, ε und pτ α = 0″0087. Dieser Winkel ist so klein, dass er sich direkten Beobachtung enzieht. Auch der durch (267) gegebene Winkel φ, der nach obigem gleich (A ⁄ C) · &945; gesetzt werden kann, ist, weil A und C fast gleich sind, von derselben Kleinheitsordnung. Dieser Winkel φ, in Bogenmass gemessen, d. h. durch 206.265 dividiert, gibt nach (267) das Verhältnis des vernachlässigten Drehimpulsanteiles zum berücksichtigten an, woraus die Kleinheit jenes ersteren Anteiles ersichtlich ist. Dadurch ist die Berechtigung des Ansatzes (256) erwiesen; dasselbe gilt auch für den Ansatz (284).
Aus den vorstehenden Angaben folgt, dass die Drehbewegung der Erde unter dem Einflusse des permanenten Anteiles des Drehmoments der Sonnen- und Mondanziehung folgenderweise geometrisch dargestellt werden kann. In einem weiten Herpolhodiekegel, dessen Achse senkrecht zur Ebene der Erdbahn steht und dessen Oeffnung rund 23°30′ beträgt, rollt, ohne zu gleiten, im positiven Drehsinne ein äusserst spitzer Polhodiekegel (mit einer Oeffnung von nur 0″0087), eine Umdrehung während eines Sterntages vollführend; der Mantel des Herpolhodiekegels wird dabei in 26.000 Jahren rückläufig abgelaufen.
§ 48. Periodische Glieder. Die Drehmomente der Sonnen- bzw der Mondanziehung auf die Erde weisen, wie vorher erlãutert, neben ihren permanenten Bestandteilen noch periodische auf. Falls man die Störungen der Mondbahn, die später besprochen werden sollen, vorläufig nicht berücksichtigt, sind die hauptsächlichsten dieser periodischen Glieder jene mit einer halbjährigen bzw. halbmonatiichen Periode. Die Wirkungen dieser periodischen Glieder auf den Rotationszustand der Erde sind bereits im § 46 analytisch dargestellt worden, so dass es sich hier nur darum handelt, die numerische Auswertung der Ausdrücke (277) und (278) für die Sonnen- bzw. Mondaziehung durchzuführen.
Der jährliche Betrag der durch die Sonnenanziehung bewirkten Präzession betrug nach vorstehenden Berechnungen 15″88. Setzt man also in (277) und (278) für pT diesen Betrag ein und für θ den bereits benutzen Wert von 23° 27′ ein, so bekommt man:
| (288) |

|
Der jährliche Betrag der durch die Mondanziehung bewirkten PrĠzession betrୂgt nach den durchgeführten Berechnungen 34″48. Umgerechnet auf di+ Dauer des siderischen Mondumlaufes bekommt man für diese Verschiebung den Wert 2″58. Dieser Wert in die Ausdrücke (277) und (278) eingesetzt, ergibt als die Wirkung der Mondanziehung
| (289) |

|
Durch diese Aenderungen, Richtungsänderungen der Drechachse der Erde, werden die Längen der Gestirne im gleichen Masse, aber in entgegengesetztem Sinne wie oben Ψ gezählt wird, betroffen. In der astronomischen Praxis pflegt man sowohl die stationären als auch die periodischen Schwankungen der Aequinoktiallinie, im retrograden Sinne positiv zu zählen, in welchem Falle man die obigen Ausdrücke für Ψ mit dem negativen Vorzeichnen zu versehen hätte. Eine genauere Ausrechnung der periodischen Glieder als sie hier vorgenommen wurde, würde eine Korrektur der Koeffizienten l″26, 0″55, 0″205, 0″089 auf l″269, 0″551, 0″204, 0″089 ergeben.
Die periodischen Aenderungen der Lage der Drehachse der Erde werden als Nutationsglieder bezeichnet und zu den Hauptgliedern der Nutation gezählt, von denen noch die Rede sein wird.
Der Frühlings- Tag- und Nachtgleichenpunkt, in dem der Aequator und die Ekliptik sich wirklich schneiden, heisst das wahre Frühlingsäquinoktium zu dieser Zeit; dagegen der von allen Nutationsgliedern befreite Durchschnittspunkt in dem sich der Himmelsäquator und die Ekliptik bloss infolge der vorstehend besprochenen Präzession schneiden würden, das mittlere Aequinoktium. In derselben Bedeutung werden die Bezeichnungen wahre und mittlere Schiefe der Ekliptik gebraucht.
Kapitel VII
Die astronomische Nutation der Erdachse.
§ 49. Störungen der Ebene der Mondbahn. Die Ebene der Bahn des Mondes um die Erde fällt nicht mit der Ebene der Ekliptik zusammen; dieser Umstand hat Störungen der Mondbewegung zur Folge, die sich auch in der Drehbewegung der Erde fühlbar machen, weshalb sie hier besprochen werden müssen.
Im § 10 ist d:s Satellitenproblem in seiner einfachsten Form behandelt und auf das Zweikörperproblem zurückgeführt worden, indem man die Voraussetzung machte, die auf den Planet bzw. auf den Satellit einwirkenden Kräfte seien untereinander parallel, Dies ist im Falle der Erde und des Erdmondes nur annähernd richtig, so dass zwecks Berechnung der erwähnten Störungen diese vereinfachende Annahme fallen gelassen werden muss.
Von den mannigfaltigen Störungen der Mondbewegung kommt für das Rotationsproblem der Erde in erster Reihe die Störung der Ebene der Mondbahn in Betracht. Um den Mechanismus und die Reichweite dieser Störung klarzulegen, ist es gestattet, von der Exzentrizität der Mondbahn abzusehen und anzunehmen, die Erde und der Mond bewegen sich um ihren gemeinsamen Massenmittelpunkt O auf kreisförmigen Bahnen, Die Halbmesser r und r1 dieser beiden Bahnen sind, wenn man, wie früher, die Masse der Erde mit M, jene des Mondes mit m1 bezeichnet, durch die Ausdrücke gegeben:
| (290) |

|
worin a1 die mittlere Entfernung des Mondes von der Erde bedeutet.
Das System Erde-Mond kann jetzt als ein geschlossenes, seine Form nicht änderndes materielles System aufgefasst werden, auf welches, als eine äussere Kraft, die Sonnenanziehung einwirkt. Dieses unveränderliche System rotiert bei seinem jährlichen Umlaufe um die Sonne um die durch den Massenmittelpunkt O hindurch gehende, auf der Ebene der Mondbahn senkrecht stehende Drehachse mit einer Winkelgeschwindigkeit ν1 die der mittleren Bewegung des Mondes um die Erde gleichzusetzen ist. Weil das auf den Punkt O sich beziehende Trägheitsellipsoid dieses materiellen Systems keine Kugel ist, wird, geradeso, wie es mit der unter dem Einfluss der Sonnenanziehung stehenden Erde der Fall gewesen ist, die soeben gekennzeichnete Drehachse dieses Systems sich verlagern müssen. Man kann die im vorigen Kapitel entwickelte Theorie der Verlagerung der Drehachse auch auf den vorliegenden Fall ungeändert anwenden, wofern man die Analogie der beiden Fälle zu einer vollständigen gestaltet.
Die Drehbewegung der Erde um ihre Achse hatte, weil die Erde ein Rotationskörper ist, keinen Einfluss auf das Drehmoment 𝕸 der äusseren Kräfte. Im vorliegenden Falle trifft dies nicht mehr zu, vielmehr wird die Drehbewegung des Systems Erde-Mond um die oben angegebene Achse zu einer periodischen Aenderung der Grösse 𝕸 Anlass geben, deren Periode der Umlauszeit T1 des Mondes um die Erde gleich ist, also die Dauer eines siderischen Monats sein wird. Die aus dieser kurzperiodischen Aenderung des Drehmoments 𝕸 sich ergebenden Störungen der Mondbahn sind zu unbedeutend, um bei den Problemen, mit denen ich mich in diesem Buche zu beschäftigen haben werde, berücksichtigt werden zu müssen und können auf folgende Weise leicht eliminiert werden.
Während des Zeitintervalles T1 vollführen Erde und Mond einen ganzen Umlauf auf ihren Kreisbahnen. Der diesem Zeitintervalle entsprechende Mittelwert des Drehmoments 𝕸 kann, wie leicht einzusehen, erhalten werden, indem man die Erdmasse M längs der Erdbahn, die Mondmasse m1 längs der Mondbahn gleichmässig verteilt sich denkt und sodann das Drehmoments 𝕸 ermittelt, mit dem die Sonne auf das System dieser beiden materiellen Ringe einwirkt. Dieser Vorgang ist gleichbedeutend mit der auch von K1ein und Sommerfeld benützten Methode der Elimination der periodischen Störungen, die Gauss bei der Berechnung der säkularen Störungen angewendet hat, nachdem er bewiesen hatte, dass die säkularen Aenderungen der Bahnen zweier sich gegenseitig störenden Planeten dieselben sind wie jene, die man erhält, wenn man diese Bahnen mit den zugehörigen Planetmassen derart belegt, dass die Masse jedes Bahnelements invers proportional wird der zugehörigen Geschwindigkeit des Planeten und sodann die Attraktion berechnet, die diese materiellen Bahnringe aufeinader ausüben. Weil in unserem Falle zufolge der gemachten Voraussetzung die Bahnen von Erde und Mond als kreisförmig zu betrachten sind, ergab sich eine homogene Verteilung der zugehörigen Massen M und m1.
Das Trägheitsmoment C der derart gestalteten materiellen Ringe bezüglich der durch den Punkt O hindurchgehenden Drehachse des Systems ist durch den Ausdruck veranschaulicht:
C = Mr2+ m1R12.
Denselben Wert weist auch das polare Trägheitsmoment J0 bezüglich des Punktes O auf. Es ist also
J0 = C
Weil nach einer allgemeinen Eigenschaft der Trägheitsmomente
A + B + C = 2J0
ist, worin A und B die beiden anderen Trägheitshauptmomente bedeuten, die aus Symmetriegründen einander gleich sind, d. h. B = A ist, so wird
2A = C
d. h.
| (291) |

|
Jetzt haben wir denselben Fall vor uns, dem wir bei der Berechnung der Präzession begegnet haben; man hat in den damals erhaltenen Formeln bloss die nachstehenden selbstverständlichen Substitutionen durchzuführen. Statt der Z-Achse des damals verwendeten Koordinatensystems, die mit der Drehachse der Erde zusammen fallend angenommen wurde, hat man die auf der Ebene der Mondbahn senkrecht stehende Achse einzuführen. Der Ursprung dieses Koordinatensystems kann, weil die Entfernung des Punktes O vom Erdmittelpunkt sehr klein ist, in disen Punkt verlegt werden. Die X-Achse des Koordinatensystems ist gegen den aufsteigenden Knoten der Ekliptik in bezug auf die Mondbahn, d. h. gegen den absteigenden Knoten dieser Bahn in bezug auf die Ekliptik zu richten. Die Länge λ der Sonne ist durch die von dem erwähnten Knotenpunkt der Mondbahn gemessene Länge λ1 zu ersetzen und anstelle der Schiefe der Ekliptik ε = Θ die Neigung ε1 der Mondbahn zur Ekliptik zu setzen. Die Drehgeschwindigkeit n der Erde ist durch die Drehgeschwindigkeit des Systems Erde-Mond, d. h. durch die mittlere Bewegung ν1 des Mondes auf seiner geozentrischen Bahn zu ersetzen. Statt der Masse M der Erde ist die Masse (M + m1) des Systems Erde-Mond einzuführen und statt des Bruches (C - A) ⁄ C der soeben angegebene numerische Wert (291) zu setzen. Auf diese Weise bekommt man statt der Formel (279) die Formel:
| (292) |

|
Die Gesamtmasse (M + m1) des Systems Erde-Mond ist im Vergleich zur Sonnenmasse m ausserordentlich klein und man kann sie oben im Nenner vernachlässigen, so dass man mit Berücksichtigung von (281) erhält:
| (293) |

|
Die Bewegung der Knoten der Mondbahn ist also eine rücklaufige. Der absolute jährliche Betrag dieser Verrückung ist gleich:
| (294) |

|
oder, in Graden gemessen,
| (295) |

|
Mit ε1 = 5° 8′ 43″; T1 = 27,322 Tage; T = 365,24 Tage bekommt mun eine jährliche Verrückung von 20°. Ein vollständiger Umlauf würde unter den oben gemachten vereinfachenden Annahmen rund 18 Jahre erfordern; in Wirklichkeit beträgt die siderische Umlaufszeit der Knoten der Mondbahn etwas mehr und zwar 18,6 Jahre.
Ausser dieser stationären Bewegung der Mondknoten weisen die Winkel Ψ und Θ der Ebene der Mondbahn periodische Schwankungen; sie ergeben sich mittels (277) und (278) und man bekommt mit dem obigen Ausdruck für pτ:
| (296) |

|
Der letztere Ausdruck besagt, dass die Neigung ε1 der Ebene der Mondbahn zur Ekliptik um ihren Mittelwert von 5° 8′ 43″ mit einer Amplitude von 8′39″ schwankt. Eine genauere Ausrechnung würde eine Korrektur dar obigen Koeffizienten 1° 36′ bzw. 8′ 39″ auf 1° 38″ bzw. 8′ 48″ ergeben.
§ 50. Die astronomische Nutation der Erdachse. Die rückläufige Bewegung der Mondknoten hat periodische Aenderungen der Rotationsachse der Erde zur Folge, die, durch die Beobachtung zuerst entdeckt, den Namen Nutation erhielten, welcher Name auch für die später entdeckten, bereits besprochenen periodischen Glieder in Anwendung kam. Es sollen nun die mathematischen Ausdrücke für jene durch die Bewegung der Mondknoten hervorgerufene Nutation im engsten Sinne des Wortes abgeleitet werden.

Sei (Fig. 21) AA′ der Himmelsäquator, EE′ die Ekliptik, LL&prime die auf der Himmelssphäre projizierte Mondbahn, es stellt dann F den Frühlingspunkt, D den aufsteigenden Knoten der Mondbahn in bezug auf die Ekliptik und C in bezug auf den Aequator dar. Es ist ferner ∢DFC = ε die Schiefe der Ekliptik, ∢L′DE′ = ε1 die Neigung der Mondahn zur Ekliptik, ∢DCA′ = ε2 die Neigung der Mondbahn zum Aequator. Es stellt schliessiich arcFD = λ1 die Länge des Knotens D und arcFC = α die Rektaszension des Knotens C dar. So wie der permanente Bestandteil des Drehmoments der Sonnenanziehung auf die Erde gegen den Frühligspunkt gerichtet war, so wird der permanente Bestandteil 𝕸s des Drehmoments 𝕸 der Mondanziehung auf die Erde gegen den Knoten C gerichtet sein und eine skalare Grösse
| (297) |

|
aufweisen. Zerlegt man dieses Drehmoment in zwei Komponenten, von denen die eine, Ms′, in die Aequinoktiallinie fällt, die andere, Ms″, sekrecht darauf steht, so sind die skalaren Grössen dieser Komponenten gleich Ms′ = Ms · cos α; Ms″ = Ms · sin α, d. h.
| (298) |

|
|
| (299) |

|
Aus dem sphärischen Dreieck FCD folgen nachstehende Gleichungen:

|
Setzt man diese Ausdrücke in (298) und (299) ein und berücksichtigt, dass

|
ist, so bekommt man:
| (300) |

|
|
| (301) |

|
In (300) stellt

|
den gegen den Frühlingspunkt gerichteten permanenten Bestandteil des Drehmoments 𝕸s. Um zu dem infolge des Umlaufes der Mondknoten periodischen Bestandteil 𝕸p dieses Drehmoments zu gelangen, ist der erstere Bestandteil, als in der lunisolaren Präzession bereits inbegriffen, auszuscheiden, wobei zu bemerken ist dass, wie der Vergleich mit (249) zeigt, jener berücksichtigte um 1,2% zu gross geraten ist wegen der vereinfachenden Annahmen, welche bei der Bildung von (280) gemacht worden sind. Auf diese Weise bekommt man für die Koordinaten M1′, M2′ des Drehmoments 𝕸p nachstehende Ausdrücke; dieselben mussten wegen den durch (250) getroffenen Vereinbarungen mit dem entgegengesetzten Vorzeichen versehen werden. Es ist also:
| (302) |

|
|
| (303) |

|
Zieht man die Gleichungen (261) heran und berücksichtigt (255), so bekommt man:
| (304) |

|
|
| (305) |

|
Es ist wegen (268) und (281)

|
Der absolute jährliche Betrag der durch die Mondanziehung bewirkten Präzession beträgt nach (280):

|
Berücksichtigt man noch, dass infolge des Rücklaufes der Mondknoten
| (306) |

|
ist worin T2 die bereits ermittelte Periode des Umlaufes der Mondknoten bedeutet, so bekommt man:
| (307) |

|
|
| (308) |

|
Die Integration dieser Gleichungen ergibt unter Beibehaltung der Initialbedingungen, wie sie der Integration der Ausdrücke (273) uud (274) zugrunde lagen:
| (309) |

|
|
| (310) |

|
Mit pT = 34″48, T2 = 18,6 · T; ε = 23° 27′; ε1 = 5° 8′ 43″ bekommt man:
| (311) |

|
In der astronomischen Praxis ist es üblich, den Winkel Ψ retrograd zu zählen, in welchem Falle die Ausdrücke für Ψ in (288), (289) und (311) mit dem entgegengesetzten Vorzeichen zu versehen sind. Ausserdem pflegt man statt der unabhängigen Variablen t die Länge ☉ der Sonne, die Länge ☾ des Mondes und die Länge ☊ des aufsteigenden Mondknotens in die Ausdrücke (288), (289), (311) einzuführen. Weil ☊ retrograd zunimmt, so ist in den Gliedern mit sin 𢘊 abermals ein ZeichenwechseI vorzunehmen. Auf diese Weise bekommt man mit Benützung der auf zwei Dezimalen genau bestimmten Werte der zugehörigen Koeffizienten folgenden Ausdruck für die Gesamtnutation:
| Ψ = -17″ 06 sin 2 ☉ - 0″ 20 sin 2 ☽ - 17″ 26 sin ☊ + 0″ 21 sin 2 ☊ | ||
| Θ = + 0″ 55 cos 2 ☉ + 0″ 09 cos 2 ☾ + 9″ 22 cos ☊ - 0″ 09 cos 2 ☊ |
Jedes gleichperiodische Paar der cbigen Glieder verursacht eine Verlagerung der Rotationsachse der Erde von solcher Art, dass der Durchstosspunkt dieser Achse mit der Himmelssphäre während der zugehörigen Periode am Himmelsgewölbe eine kleine Ellipse, die Nutationsellipse, beschreibt. Einer Richtungsänderung der Erdachse um Θ und Ψ entsprechen nämlich die scheinbaren Verrückungen x = Θ y = Ψ sin ε auf der Himmelssphäre und man bekommt beispielsweise fü die beiden Hauptglieder der obigen Ausdrücke &252;r die Gesamtnutation:
| x = 9″ 22 cos ☊; y = -17″ 26 sin ε sin ☊ |
Eliminiert man aus diesen beiden Gleichungen ☊, so bekommt man

|
als die Gleichung der Bradleyschen Nutationsellipse. Ihre Halbachsen sind, weil ε = 23°27′ ist, a = 9″22; b = 6″87; die grosse Halbachse ist dabei gegen den Pol der Ekliptik gerichtet.
Kapitel VIII
Zeitmessung und Zeitzählung.
§ 51. Stern- und Sonnentage. Die Drehbewegung der Erde ist die natürliche Grundlage unserer Zeitmessung und Zeitzählung; der Zeitmessung, weil diese Bewegung die gleichmässigste ist, die wir kennen, der Zeitzählung, weil sie den Wechsel von Tag und Nacht verursacht, auf deren Ablauf unsere ganze Lebensweise und Tätigkeit eingerichtet ist.
Die Winkelgeschwindigkeit der Eigenrotation der Erde um ihre Figurenachse ist nach (241) eine konstante Grösse, so dass diese Rotation volkommen gleichmässig erfolgt. Hätte man also eine auf der Himmelskugel, wie angenagelt, befestigte Marke, so würde diese den Zeiger der irdischen Uhr dastellen, weil sich dieser Punkt relativ zum irdischen Beobachter längs seines Parallelkreises gleichmässig bewegen und sein Stundenwinkel das Mass der Zeit getreulich angeben würde.
Es ist aber unmöglich einen mit der Himmelssphäre fest verbundenen Punkt namhaft zu machen, weil das Netz der Fixsterne, trotz ihren Namens, kein fixes ist. Man war deshalb veranlasst, einen, zwar beweglichen, aber als Schnitt des Himmelsäquators und der Ekliptik wohl definierten Punkt der Himmelssphäre, den Frühlingspunkt, als den Zeiger der irdischen Uhr zu benützen, und seinen Stundenwinkel die Sternzeit zu nennen. Die Winkelgeschwindigkeit der Erdrotation relativ zum Frühlingspunkt ist im vorstehenden Kapitel mit Φ′ bezeichnet worden; der Zusammenhang zwischen dieser Winkelgeschwindigkeit und der Winkelgeschwindigkeit n der Eigenrotation der Erde war durch (242), d. h. durch Φ′ + Ψ′cos θ = n gegeben, worin Ψ′ die Präzessionsgeschwindigkeit des mittleren Aequinoktiums und θ die mittlere Schiefe der Ekliptik bedeutet. Wenn Ψ′ und θ konstante Grössen wären, würde aus der Konstanz von n auch jene von Ψ′ folgen und die Verwendbarkeit der täglichen Bewegung des Frühlingspunktes zum Zeitmass wäre ohne weiters erwiesen. Die Grösse Ψ′ ist aber nicht konstant, sondern, weil wir hier mit dem mittleren, also von periodischen Schwankungen befreiten Aequinoktium zu tun haben, säkular veränderlich; dasselbe gilt auch hinsichtlich der Grösse θ. Es ist indessen folgendes zu berücksichtigen. Der Frühlingspunkt braucht zum vollständigen Umlauf längs der Ekliptik rund 26.000 Jahre oder rund 9,5 Millionen Sterntage, weshalb die Präzessionsgeschwindigkeit Ψ′ 9,5 Millionen Mal kleiner ist als die Rotationsgeschwindigkeit der Erde. Das Glied Ψ′ · cos θ der obigen Gleichung ist also im Vergleich zu den übrigen sehr klein und die säkularen Aenderungen dieses Gliedes, die nur einen geringen Bruchteil desselben erreichen, beeinflussen die durchschnittliche Dauer des Sterntages nur ganz unmerklich. Aus diesem Grunde kann auch der Stundenwinkel des mittleren Frühlingspunktes zum praktischen Mass der Zeit benützt werden.
Für das bürgerliche Leben ist der Sterntag als Mass der Zeit nicht gut brauchbar, weil sein Beginn im Laufe des Jahres nach und nach alle Stunden des Sonnentages durchlaufen würde. Aus diesem Grunde muss im bürgerlichen Leben, welches auf den regelmässigen Wechsel von Tag und Nacht eingerichtet ist, mit der Sonnenzeit gezählt werden. Es ist bereits im § 41 angegeben worden, was unter wahrem Sonnentag, wahrem Mittag und wahrer Sonnenzeit zu verstehen ist; die dort mitgeteilten Angaben mögen durch die folgenden ergänzt werden.
Weil sich die Sonne auf ihrer scheinbaren jährlichen Bahn um die Erde nicht mit gleicher Winkelgeschwindigkeit bewegt, sondern mit einer veränderlichen, die dem zweiten Keplerschen Gesetz genügeleistet, weil überdies diese Bahn gegen den Himmelsäquator geneigt ist und deshalb selbst einer gleichmässigen Zunahme der Sonnenlänge keine solche der Rektaszension entsprechen würde, ist die Dauer der wahren Sonnentage im Laufe des Jahres veränderlich. Um diese Unzukömmlichkeit zu beseitigen und ein gleichförmiges, von der täglichen Bewegung der Sonne abhängiges Zeitmass zu gewinnen, denkt man sich die wahre Sonne durch eine andere, die sogenannte erste mittlere Sonne, ersetzt, deren Anomalie gleichmässig zunimmt und die mit der wahren Sonne gleichzeitig die Apsidenlinie durchschreitet; dadurch erscheinen die wirklichen Ungleichheiten in der Bewegung der wahren Sonne beseitigt. Um auch die andere aus der Schiefe der Ekliptik herrührende Ungleichheit in der Bewegung in Rektaszension wegzuschaffen, denkt man sich eine zweite mittlere Sonne, die sich längs des Aequators derart bewegt, dass sie mit der ersten mittleren Sonne zugleich die Aequinoktialpunkte durchreitet; die Rektaszension der zweiten mittleren Sonne ist also stets gleich der Länge der ersten mittleren Sonne. Die Zeit zwischen zwei aufeinanderfolgenden Kulminationen der zweiten mittleren Sonne heisst ein mittlerer Sonnentag; es ist mittlerer Mittag im Augenblicke der Kulmination derselben und die mittlere Zeit in irgend einem Augenblicke wird durch den Stundenwinkel dieser zweiten mittleren Sonne gemessen. Im bürgerlichen Leben seit langem und in der astronomischen Praxis seit 1925 ist es üblich, den mittleren Sonnentag von Mitternacht bis Mitternacht zu zählen u. zw. von 0h bis 24h oder in je zwei gleichen Perioden von 0h bis 12h.
Aus dem vostehendem folgt, dass die Sternzeit durch den Stundenwinkel des Frühlingspunktes, die wahre Sonnenzeit durch den Stundenwinkel der Sonne und die mittlere Sonnenzeit durch den Stundenwinkel der zweiten mittleren Sonne gemessem wird. Wird dabei dieser Stundenwinkel vom Meridiane des Standortes gezählt, so heissen jene Zeiten Ortszeiten. Zwei Orte, die unter verschiedenen Meridianen liegen, haben, wie leicht einzusehen, in demselben Augenblicke eine verschiedene Ortszeit, und der Unterschied, dieser Ortszeiten ist gleich dem im Zeitmasse gemessenen Längenunterschied beider Orte. Mit der Entwicklung der Verkehrsmittel und namentlich seit der Einführung der Eisenbahnen musste die auf die Ortszeit gegründete Zeitmessung, nach der jedem Orte seine eigene lokale Zelt zukommt, fallengelassen werden und es führten zuerst die Bahnverwaltungen Einheitszeiten ein, die mit der Ortszeit der Landeshauptstadt oder oder eines andern passend gewählten Ortes übereinstimmten. Nach und nach bürgerte sich diese Art der Zeitmessung in Form von Landeszeiten im privaten und öffentlichen Leben ein, um allmählich auf eine noch zweckmässigere Grundlage gestellt zu werden. Vor allem wurde die Ortszeit des Greenwicher Meridianes als die Weltzeit allgemein anerkannt. Es wurde weiters nach einem Vorschlag von Fleming die ganze Erde durch vierundzwanzig voneinander um 15° abstehende Meridiane in ebensoviel Kugelzweiecke, die man fälschlich als Zonen bezeichnete, geteilt, von denen das erste Kugelzweieck durch den Meridian von Greenwich halbiert erscheint. Führt man also in jeder dieser Zonen Einheitszeiten ein, die dem mittleren Meridian der Zone entsprechen, so werden diese Zonenzeiten um eine ganze Anzahl von Stunden von der Weltzeit sich unterscheiden. Dieser auf Zonenzeiten beruhenden Zeitmessung haben sich fast alle Staaten der Erde weitgehend angepässt.

Der Unterschied zwischen der wahren und mittleren Zeit irgend eines Ortes der Erde wird die Zeitgleichung genannt. Die Ermittlung der Zeitgleichung gründet sich auf der analytischen Lösung des im Kapitel II behandelten Problems des Umlaufes der Erde um die Sonne; man findet den Wert der Zeitgleichung für jeden Tag des Jahres in den astronomischen Ephemeriden angegeben. In Fig. 22 ist die Aenderung der Zeitgleichung im Laufe des Jahres 1931 graphisch dargestellt; der Unterschied, der sich für ein anderes Jahr der Gegenwart ergeben würde, ist unbedeutend. Man ersieht aus dieser Darstellung, dass viermal im Jahre, am 16. April, 15. Juni, 2. September und 25. Dezember, die Zeitgleichung gleich Null ist. Am 12. Februar bzw. am. 25. Juli erreicht die Zeitgleichung ihre positiven Maximalwerte, von denen der erste 14 min 23 sec, der zweite 6 min 23 sec beträgt; am 15. Mai bzw. am 4. November erreicht die Zeitgleichung ihre negativen Maximalwerte, von denen der erste 3 min 47sec, der zweite 16min 23 sec beträgt.
§ 52. Zeitzählung. Der Sonnentag ist eine viel zu kleine Einheit, als dass mit derselben längere Zeitintervalle gemessen oder Ereignisse datiert werden könnten. Deshalb ist die Datierung nach Tagen allein nur ausnahmsweise im Gebrauch, so nach der Scaligerschen Zählung (Julianische Periode), die mit dem 1. Januar 4713 vor Christi beginnt und nach der der 1. Januar 1940 mit 2429630 zu datieren ist. Grössere Einheiten der Zeitzählung sind seit jeher in Anwendung gekcmmen: die Woche, der Mond und das Jahr, von denen die zwei letzteren Einheiten den Naturerscheinungen, dem Wechsel der Lichtgestalten des Mondes bzw. dem Ablauf der Jahreszeiten entnommen wurden, die Zählung nach Monden aber diese Bedeutung grösstenteils verlor, weil der Wechsel der Lichtgestalten des Mondes mit dem Lauf der Jahreszeiten schwer in Einklang zu bringen war. Nach Mondmonaten wird in christlichen Kalender nur bei der Festlegung des Osterfestes gerechnet, während der Kalender der Mohammedaner und jener der Juden nach Mondmonaten aufgebaut ist.
Die Umlaufszeit der Erde um die Sonne, oder anders gesprochen, die Zeit während der die Sonne auf der scheinbaren Himmelskugel einen vollständigen Umlauf vollführt, heisst das siderische Jahr. Die Länge des siderischen Jahres ist, wie bereits berichtet, als konstant zu betrachten und beträgt 365 Tage 6 h 9 m 9 s. Diese Zeitspanne ist die natürliche Einheit, mit der der Gang der Erde im Weltall gemessen werden kann, für die Naturerscheinungen, die sich auf der Erde selbst abspielen, ist sie es nicht. Der Ablauf der Jahreszeiten geht nämlich mit den Durchgangszeiten der Sonne durch die Aequinoktialpunkte Hand in Hand, zu welchen Zeiten auf der ganzen Erde Tag und Nacht einander gleich sind. Die Zeit, die die Sonne braucht, um vom Frühlingspunkt ausgehend wieder zu demselben zurückzukehren, heisst das tropische Jahr. Weil der Frühlingspunkt jährlich um den Betrag der allgemeinen Präzession auf der Ekliplik sich rückläufig bewegt, also der Sonne entgegengeht, ist das tropische Jahr kürzer als das siderische und beträgt gegenwärtig 365d 5h 48m 46s = 365,24220d. Diese Grösse ist, weil von den Störungen der Erdbahn abhängig, säkular schwach veränderlich.
Aus der Länge des tropischen Jahres ergibt sich der Zusammenhang zwischen der mittleren Sonnenzeit und der Sternzeit. Während des tropischen Jahres durchläuft auch die mittlere Sonne den Weltäquator von West nach Ost und hat deshalb für jeden Ort der Erde einen Meridiandurchgang weniger als es solcher dem Frühlingspunkte zukommen. Das tropische Jahr hat daher genau um einen Sterntag mehr Sterntage als mittlere Sonnentage. Daraus ergibt sich die Beziehung:
- 366,2422 Sterntage = 365,2422 mittlere Sonnentage,
die zur Umrechnung der Sternzeit in mittlere oder umgekehrt dient.
Handelt es sich darum, eine Zeitzählung zu schaffen, die mit dem Lauf der Jahreszeiten im Einklang ist, so ist es erforderlich, aus den gegebenen zwei natürlichen Zeiteinheiten, dem Tag und dem tropischen Jahr, einen Kalender zu bilden, in dem das Jahr eine ganze Anzahl von Tagen umfasst, aber eine mittlere Länge aufweist, die jener des tropischen Jahres möglichst nahe kommt. Dieses Problem haben bereits die Alexandriner in einer ersten Annäherung glücklich gelöst. Wie dies durch die von Lepsius entdeckte Steininschrifft, dem "Edikt von Kanopus" (datiert mit der 19. Tybi des neunten Jahres von Euergetes, d.h. mit dem 7 März 238 v. Chr) einwandfrei festgestellt ist, hat im Jahre 238 v. Chr. die ägyptische Priesterschaft beschlossen, dem ägyptischen Kalenderjahre von 365 Tagen alle vier Jahre einen Schalttag hinzuzufügen. Durch dieses Schaltverfahren erhielt das Kalenderjahr eine mittlere Länge von 365d 6h und kam der oben angegebenen Länge des tropischen Jahres auf 11m 14s nahe. Es ist für die Würdigung dieser Leistung der Alexandriner belanglos, ob diese Kalenderreform zu jener Zeit tatsächlich durchgeführt wurde, sicher ist es, dass sie zwei Jahrhunderte später zur Basis des römischen und nachher des christlichen Kalenders wurde. Die Römer teilten das bürgerliche Jahr in 12 Monate: martius, aprilis, maius, junius, quintilis, sextiiis, september, october, november, december, januarius und februarius, deren Dauer von der willkürlichen Bestimmung des Pontifex maximus abhing. Da man sich bei dieser Bestimmung um die Länge des Sonnenjahres nicht vier kümmerte, kam der römische Kalender in eine solche Unordnung, dass sich Ju1ius Cäsar als Pontifex maximus veranlasst sah, hier Wandel zu schaffen. Zu jener Zeit und bis zu Cäsars Tode weilte in Rom Aegyptens Königin Kleopatra, Cäsars ungetraute Gattin. In ihrem königlichen Gefolge befanden sich auch einige Gelehrte des alexandrinischen Museums, darunter der Astronom Sosigenes, der zum geistigen Vater der Julianische Kalenderreform wurde, deren Schaltverfahren nur eine Neuanflage des Ediktes von Kanopus darstellt. Im Jahre 325 wurde der Julianische Kalender durch den Konzi1 von Nicäa von der christlichen Kirche angenommen.
Im Julianischen Kalender ist jedes vierte Jahr und zwar jenes, deren Jahreszahl durch 4 restlos teilbar ist, ein Schaltjahr. Als Schalttag dient gegenwärtig der 29. Februar. Die Längen der einzelnen Monate, deren Aufzählung hier überflüssig ist, sind recht ungleichmässig verteilt, auch die Bezeichnungen September, Oktober, November, Dezember entsprechen ihrer gegenwärtigen Stellung in der Reihenfolge der Monate nicht mehr; der römische Monat quintilis erhielt zu Ehren Cäsars den Namen Julius, sextilis zu Ehren Augustus dessen Namen.
Im Laufe der Jahrhunderte machte sich der Unterschied von 11m 14s zwischen der mittleren Länge des Julianischen Kalenderjahres und der Länge des tropischen Jahres deutlich fühlbar. Das Frühlingsäquinoktium, das zur Zeit des Konzils von Nicäa am 21. März stattfand, traf im 16. Jahrhundert schon zehn Tage früher ein, und es ergab sich die Notwendigkeit einer neuen Kalenderreform, die dieses Abrücken des Aequinoktiums beseitigen und in Zukunft verhindern sollte. Das grosse Verdienst, eine solche Heform des Kalenders, deren Notwendigkeit bereits im 14. und 15. Jahrhundert erkannt wurde, durchgeführt zu haben, gebührt dem Papst Gregor XIII. Durch diese Reform, die den Kalender neuen Stils, den Gregorianischen, schuf, wurden nach den von Luigi Lilio herrührenden Vorschlägen folgende Aenderungen an dem bestehenden christlichen Kalender vorgenommen. Um die Aequinoktien an die ursprüngliche Stelle im Kalender zurückzuversetzen, wurden 10 Tage aus dem Kalender ausgelassen, indem der 5. Oktober 1582 des Julianischen Kalenders mit dem 15. Oktober datiert wurde. Um überdies die mittlere Länge des Kalenderjahres mit der Länge des tropischen Jahres in Einklang zu bringen, wurde das nachstehende Schaltverlahren eingeführt: Schaltjahre sollen, wie bisher, jene Jahre sein, deren, Jahreszahl mit 4 restlos teilbar ist, mit Ausnahme der Säkularjahre. Diese, deren Jahreszahl mit zwei Nullen endigt, sollen nur dann Schaltjahre sein, wenn die Anzahl ihrer Jahrhunderte durch 4 restlos teilbar ist. So war im Gregorianischen Kalender von den Säkularjahren nur das Jahr 1600 ein Schaltjahr, während es in Zukunft die Jahre 2000, 2400, 2800 u. s. f. sein sollen. Es folgt aus dieser Schaltregel, dass der Gregorianische Kalender in 400 Jahren 3 Tage weniger aufweist als der Julianische, weshalb die mittlere Länge seines Jahres in Tagen
- 365,25 - 3 ⁄ 100
beträgt, d. h. 365,2425 Tage oder 365d 5h 49m 12s. Dadurch wurde der Unterschied zwischen dem tropischen Jahr und dem mittleren Kalenderjahr von 11m 14s auf 26s herabgedrückt.
Die Gregorianische Kalenderreform wurde in den katholischen Ländern rasch durchgeführt, in den protestantischen nach Sträuben und Gegenvorschlägen, viel später, so in England erst im Jahre 1752.
Die griechisch-orthodoxe Kirche hielt am Julianischen Kalender fest, um erst im Jahre 1923 die dringend notwendige Reform desselben zu beschliessen. In diesem Jahre wurde vom ökumenischen Patriarchen Me1etius IV. ein Kongress der orthodoxen orientalischen Kirchen (worunter in erster Linie die russische, die griechische, die serbische und die rumänische zu nennen sind) in Konstantinopel einberufen, auf dem beschlossen wurde, den bereits auf 13 Tage angewachsenen Unterschied zwischen dem Kalender der westlichen und jenen der östlichen Kirchen verschwinden zu lassen, aber bei der Verteilung der Schaltjahre die seit der Gregorianischen Kalenderreform erzielten Fortschritte der astronomischen Wissenschaft im vollen Masse zu berücksichtigen. Um aber durch diese Massregel keine praktisch fühlbare Divergenz mit dem Gregorianischen Kalender zu schaffen, wurde auf meinen Vorschlag folgende Schaltregel angenommen. Die Schaltjahre werden, wie bisher, jene Jahre sein, die restlos durch 4 dividiert werden können; eine Ausnahme bilden, wie im Gregorianischen Kalender, die Säkularjahre, die aber nur dann Schaltjahre sein werden, wenn die Anzahl ihrer Jahrhunderte, durch 9 dividiert, den Rest 2 oder 6 ergibt. Es werden also von den kommenden Säkularjahren nur die Jahre 2000, 2400, 2900, 3300 u. s f. Schaltjahre sein. Diese Schaltregel bewirkt folgendes. Ein- Auseinandergehen vom Gregorianischen Kalender wird erst im Jahre 2800 stattfinden. Der neue Kalender weist in 9 Jahrhunderten 7 Tage weniger als der Julianische auf, weshalb die mittlere Länge seines Jahres in Tagen
- 365,25 - 7 ⁄ 900
beträgt, d. h. 365,24222 Tage oder 365d 5h 48m 48s, sich also nur um 2 Sekunden von der gegenwärtigen Länge des tropischen Jahres unterscheidet.
Dritter Abschnitt
Säkulare Wanderungen der Drehpole der Erde
Kapitel IX
Das Polwanderungsproblem und seine mathematische Erfassung
§ 53. Geschichtliches. Die klassische Theorie der Drehbewegung der Erde ist aus der Voraussetzung der Starrheit des Erdkörpers entstanden. Obwohl eine solche Annahme nur unvollständig der Wirklichkeit entsprach, war diese Theorie, wie im Vorhergehenden Abschnitt dargetan, imstande, die astronomisch festgestellten Eigentümlichkeiten der Drehbewegung der Erde, die Präzession und die astronomische Nutation der Erdachse, auf das befriedigendste zu erklären und mathematisch exakt darzustellen. Kein Wunder also, dass anderthalb Jahrhunderte seit der Begründung dieser Theorie verflossen waren, ohne dass man es unternommen hatte, an der gemachten, scheinbar wohlerprobten Annahme zu rütteln.
Erst um die Mitte des vorigen Jahrhunderts gab die aktuell gewordene Frage nach dem Zustand des Erdinnern Veranlassung zur Erörterung des Problems, wie die Präzessions- und die Nutationsbewegung der Erdachse verlaufen müssten, wenn die Erde ein flüssiges, in einer festen Schale eingeschlossenes Innere besässe. Fast sieben Jahrzehnte hat man sich mit dieser Frage befasst, um schliesslich durch die Arbeiten Oppenheim′s und Poincaré′s dahin zu gelangen, dass eine flüssige Erde dieselbe Präzessionsbewegung vollführen würde wie eine starre, was Schweydar auch hinsichtlich einer elastischen bewies. Es lag also keine Veranlassung vor, die klassische Theorie durch eine neue zu ersetzen, Wohl hat die Entdeckung der Chandlerschen Periode der freien Nutation der Erdachse gezeigt, dass man dabei mit der klassischen Annahme des starren Erdkörpers kein Auslangen finden könne, doch genügte, wie bereits erwähnt, die Annahme eines festen aber elastischen Erdkörpers, um auch diese Erscheinung befriedigend zu erklären.
Durch die vorstehend angeführten glänzenden Ergebnisse der exakten Wissenschaften blieb aber eine, ja vielleicht die wichtigste Frage der Geophysik unbeantwortet. Geologische Forschungen haben nach und nach erwiesen, dass die Drehpole der Erde nicht mit deren Kruste fest verbunden sind, dass sie vielmehr im Verlauf der Erdgeschichte weite Wege auf der Erdoberfläche zurückgelegt haben. Zahlreiche Dokumente der erdgeschichtlichen Vergangenheit, namentlich jene, die uns von dem Klima der geologischen Vorzeit Kunde geben, sprechen deutlich für die Wandelbarkeit der Erdpole. So haben, um nur einige diesbezügliche Belege anzuführen, die mächtigen frühkarbonischen Kohlenvorräte Spitzbergens wohl nicht an der gegenwärtigen geographischen Breite dieser Inselgruppe sich bilden können. Dies konnte nur in den äquatorialen Regenzonen oder jenen der gemässigten Breiten geschehen sein. Dies beweist, dass während des Karbons die Lage der Erdpole und des zugehörigen Erdäquators eine andere war als heute und dies gilt auch für die übrigen Epochen der Erdgeschichte. So haben die Geologen, soviel dies bei dem ständig sich ändernden AntIitz der Erde möglich ist, die jeweilige Lage der Erdpole Schritt für Schritt durch die Zeitalter der Erdgeschichte verfolgen und, nachweisen können, dass diese Pole weite Wege auf der Erdoberfläche zurückgelegt haben.
Dieser von der Geologie aufgerollten Frage von der Wanderung der Erdpole standen die exakten Wissenschaften lange Zeit ratlos gegenüber. Die in der zweiten Hälfte des vorigen Jahrhunderts von W. Thomson, G. H. Darwin, Löffelholz von Colberg und Schiaparelli unternommenen Versuche, diese Frage mit Hilfe der Mechanik zu beantworten, blieben erfolglos, worübber auch Tisserand in seinem grossen Werke berichtet hat. Die angesehensten von diesen Forschern machten für die Verschiebung der Pole geologische Massenverlagerungen verantwortlich, durch welche die Lage der Trägheitspole und damit auch jene der Drehpole in Mitleidenschaft gezogen wurde. Derartige Massenverlagerungen haben während der Erdgeschichte tatsächlich stattgefunden, die quartäre Vereisung, über die noch ausführlich die Rede sein wird, ist ein Beispiel dafür. Aber selbst die durch diese Vereisung stattgefundenen Massentransporte, die uns auf den ersten Blick riesig erscheinen, waren, wie dies rechnungsmässig bewiesen werden kann, ganz ungenügend, um grössere Verlagerungen der Drehpole hervorzurufen, Die exakten Wissenschaften schienen also ausserstande zu sein, greifbare mechanische Ursachen für grosse Verlagerungen der Erdpole, wie solche von den beschreibenden Naturwissenschaften gefordert wurden, ausfindig zu machen. Der Mechanismus solcher Polwanderungen blieb trotz aller Bemühungen derart ungeklärt, dass selbst ihre Möglichkeit in Frage gestellt schien. Als deshalb im Jahre 1927 B. Gutenberg an die Herausgabe des "Handbuches der Geophysik" schritt, sah er sich veranlasst, die ungelöst gebliebene Frage der Verlagerung der Erdpole wieder aufzugreifen und mir deren Beantwortung anzuvertrauen. Für die Klärung dieser Frage war der Abschnitt "Säkulare Polverlagerungen" des ersten Bandes jenes Handbuches vorgesehen. In demselben habe ich vorerst die erwähnten Versuche, diese Frage zu lösen, analysiert und kritisch besprochen, um in′s Reine zu gelangen, warum sie erfolglos geblieben sind. Es ergab sich dabei, dass zur Zeit als diese Versuche unternommen wurden, gewisse grundlegende geophysikalische Tatsachen nicht genügend oder gar nicht bekannt gewesen sind, und ohne Kenntnis derselben war das Problem der Polwanderungen nicht zu lösen. Also nicht Mangel an Scharfsinn und Begabung, sondern Mangel an erforderlichem Tatsachenmaterial war es, der die erwähnten Forscher an der Lösung des gestellten Problems hinderte. Es ist deshalb nicht mein persönliches Verdienst, dass ich mich vier Jahrzehnte später bei Inangriffnahme desselben Problems in einer günstigeren Lage befand als jene hervorragenden Forscher. Ich habe im Vorwort geschildert, wie ich mich mit dem zur Lösung des Problems erforderlichen Material vertraut machte, das jetzt kurz besprochen werden möge.
§ 54. Geophysikalische Tatsachen. Denkt man sich die Meeresbedeckungen der Erde entfernt, so zeigt die Oberfläche des dadurch blossgelegten Erdkörpers ein stark modelliertes Relief, in dem der schroffe Gegensatz zwischen Kontinent und Ozeanbecken deutlich in die Augen springt, weist doch die mittlere Tiefe des gesamten Weltmeeres den Betrag von rund 3.800 m auf, während die mittlere Höhe des über den Meeresspiegel emporragenden Festlandes rund 820 m beträgt. Berücksichtigt man, dass die grösste bekannte Meerestiefe 10.800 m misst, während der höchste Berggipfel den Meeresspiegel um 8.840 m überragt, so ergibt sich daraus eine Profiltiefe des Reliefs der festen Erdoberfläche von fast 20.000 m. Schweremessungen haben überraschenderweise ergeben, dass trotz dieser Unregelmässigkeiten der Erdoberfläche die Schwerkraft bei weitem nicht in dem zu erwartend en Masse von dem ihr nach der geographischen Breite zukommenden Normalwert abweicht, sondern dass jede kontinentale Massenanhäufung durch unterirdische Massendefekte und die an den Ozeanen in Erscheinung tretenden Massendefekte durch unterirdische Massenüberschüsse kompensiert erscheinen. Daraus muss gefolgert werden, dass die feste Erdrinde derart gelagert sei, als ob sie auf einer flüssigen Unterlage unter Wahrung des Tauchgleichgewichts schwimmen würde. Dieser Zustand hat den Namen "Isostasie" erhalten, denn das dem archimedischen Prinzip gehorchende hydrostatische Gleichgewicht, das hier verwirklicht erscheint, rührt, nicht etwa von einem flüssigen Aggregatzustande der erwähnten Unterlage her, die unter gewissen Einschränkungen, von denen sofort die Rede sein wird, als fest zu betrachten ist. Es könnte auf den ersten Blick erscheinen, dieser hydrostatische Gleichgewichtszustand, der bereits im Clairautschen Theorem zum Ausdruck gekommen ist, sei nur das erstarrte Abbild eines sehr frühen Entwicklungsstadiums unserer Erde, wo sie, aus ihrem astralen Zustand in jenen eines abgekühlten Himmelskörpers übergehend, sich mit einer festen Kruste zu umhüllen begann und die leichteren, zuerst erstarrten Teile derselben auf dem noch feuerflüssigen Reste geschwommen haben mussten wie Eisschollen auf dem Wasser. Einer solchen Annahme widersprechen aber triftige Argumente. Seit jener Jugendzeit der Erde ist die ganze geologische Vorzeit verflossen und während derselben hat sich das Antlitz der Erde tief verändert und ist noch immer in ständiger Wandlung begriffen. Einige dieser Veränderungen beweisen, dass jener hydrostatische Auftrieb noch immer wirksam ist. Die postglaziale Hebung Fennoskandiens, die durch die Wegräumung der während der letzten Eiszeit hier lastenden Inlandeisbedeckung zustande gekommen ist und die noch immer andauert, ist ein schlagender Beweis für die Wirksamkeit jenes hydrostatischen Druckes. Er beweist, dass die Unterlage der Kontinentaltafeln gewisse Eigenschaften flüssiger Körper besitzen muss und nicht als fest im gewöhnlichen Sinne dieses Wortes zu betrachten ist. Wie ist dies zu verstehen?
Der Begriff des starren Körpers ist ein ideeller Begriff; absolut starre Körper gibt es in Wirklichkeit nicht. Sie sind alle gegen genügend grosse Kräfte als nachgiebig zu betrachten. Wenn dabei beim Verschwinden dieser Kräfte ein fester Körper seine ursprüngliche Form wieder vollständig annimmt, wird er als vollkommen elastisch, wenn er dagegen im deformierten Zustande verbleibt, als vollkommen plastisch bezeichnet. Auch dies sind ideelle, in Wirklichkeit nie vollkommen vorhandene Eigenschaften, die nur als Grenzfälle zu betrachten sind. Von ganz besonderem Interesse sind die Eigenschaften solcher Körper, die sich gegen kurzandauernde Kräfte wie fest, gegen langandauernde wie flüssig verhalten. Man kann sie als zähflüssig, d. h. als Flüssigkeiten mit sehr grosser innerer Reibung, Viskosität, betrachten, wobei auch die kleinste Kraft, falls sie genügend lang andauert, diese Reibung zu überwinden vermag, Ein solcher Körper ist gewissermassen ein Zwischending zwischen einem festen und einem flüssigen. Das harte Pech ist ein Beispiel dafür, wie man es im Baugewerbe täglich beobachten kann. Will man ein Fass solchen, nicht angewärmten Pechs ohne Verzug entlehren, dann muss der Boden des Fasses entfernt und sein Inhalt mit Axt und Hammer zerstückelt werden, gegen deren Schläge sich das Pech wie ein harter glasförmiger Körper verhält. Kippt man dagegen das geöftnete Fass um und lässt es in dieser Lage einige Tage ruhig liegen, dann fliesst aus demselben sein Inhalt allmählich von selbst heraus. Solche Körper werde ich, im Gegensatz zu den flüssigen, "fluiden", als "fluidal" bezeichnen. Die Fluidalität ist gewissen Körpern in natürlichem Zustande eigen, bei einigen tritt sie auf, wenn sie sehr starken Drucken unterworfen werden; auch kann man feste Körper durch Temperaturerhöhung flüssig machen.
Nach dem soeben gesagten muss die Unterlage der Erdrinde ebenfalls fluidale Eigenschaften besitzen, sonst wäre ihr erwähnter hydrostatischer Auftrieb nicht verständlich und die Erscheinung der Isostasie nicht erklärlich.
Diese von der Fluidalität ihrer Unterlage herrührende isostasische Lagerung der Erdkruste soll bei den nachstehenden Untersuchungen gebührend berücksichtigt werden. A1fred Wegener hat sie zur Grundlage seiner bekannten Theorie von der Entstehung der Kontinente und Ozeane gemacht. Sein ursprüngliches diesbezügliches Grundschema war das folgende. Die Kontinente der Erde sind aus festem Baumaterial geformt, das mit dem Sammelnamen "Sial" bezeichnet werden kann, weil Silicium und Aluminium die charakteristischen chemischen Elemente der darin vorherrschenden Gesteinsarten sind. Diese Kontinentaltafeln sind in dem fluidale Eigenschaften aufweisenden "Sima" (nach Siiicium und Magnesium) isostasisch eingebettet, welch letzteres auch den Boden der Ozeane bildet. Seit der Aufstellung dieses originellen und durch seine Einfachheit gewinnenden Schemas sind schon drei Jahrzehnte verflossen und während dieser Zeit hat es sich als notwendig erwiesen, an demselben Aenderungen vorzunehmen. Das durch die neuesten Tiefseeforschungen immer deutlicher zutage tretende unregelmässige ReIief des Meeresbodens spricht gegen die Fiuidaiität desselben, denn in einem solchen Falle müsste seine Oberfläche eingeebneter sein. Es ist deshalb anzuhmen, dass auch der Boden der Ozeane oder wenigstens weite Teile desselben ebenfalls aus festem Material gebildet sein müssten. Auch hinsichtlich der Zweiteilung des Baumateriales der Erdkruste in Sial und Sima haben sich Schwierigkeiten ergeben. Für das hier zu behandelnde mechanische Problem kommen nur die darauf bezug habenden Eigenschaften des Baumaterials der Erdkruste in Betracht, nämlich ob dasselbe unter den gegebenen Umständen als fest oder als fluidal zu betrachten ist. Weil die Fuidalität auch eine Folge des im Erdinnern wirksamen Druckes oder der dort herrschenden Temperatur ist, will ich mich von den an chemische Eigenschaften gebundene oder erinnernde Bezeichnungen "Sial" und "Sima" freimachen und jenen Teil der Erdkruste, der als fest zu betrachten und der auf dem darunterliegenden Teil im Tauchgewicht gelagert ist, als die "isostasische Decke der Erde", den darunterliegenden Teil als deren "fluidale Unterlage", mitunter auch als den "fluidalen Erdkern" bezeichnen.
Die soeben besprochenen geophysikalischen Tatsachen sollen nun zwecks weiterer Verwendung in mathematischer Sprache zum Ausdruck gelangen.
§ 55. Mathematische Erfassung des vorstehenden Tatsachenmaterials. Aus den vorstehend geschilderten Tatsachen ergibt sich das folgende physikalische Bild von dem Bau und der Beschaffenheit der Erde. Der gegen kurz andauernde Kräfte als fest, gegen langandauernde als nachgiebig zu betrachtende Erdkörper ist mit einer festen, ungleichmässig dicken, ausgedehnte Meeresbedeckungen tragenden Schicht bedeckt, die ihn ganz oder teilweise umhüllt, isostasisch auf der fluidalen Unterlage ruht und die Formänderungen, denen sie unterworfen ist, unter Wahrung des Gleichgewichts vollführt.
Denkt man sich an einer beliebigen Stelle der Erde durch ihre isostasische Decke einen vertikalen gegen Wassereinbruch geschützten, genügend weiten Schacht bis zu ihrer fluidalen Unterlage vorgetrieben, so wird wegen der geschilderten Eigenschaften des fluidalen Baumaterials der Erde dasselbe in einem solchen Schacht langsam aufsteigen bis nach genügend langer Zeit in einer bestimmten Höhe der hydrostatische Gleichgewichtszustand erreicht sein wird. Setzt man voraus, dass in dem hinsichtlich seiner Tiefe ziemlich beschränkten Bereiche, der beiden nachstehenden Untersuchungen in Betracht kommt, das fluidale Material homogen ist und eine konstante Dichte aufweist, so wird die erreichte Höhenlage des fluidalen Materials, wo immer man sich den erwähnten Schacht abgeteuft denkt, einer und derselben Aequipotentiaifläche des Schwerkraftfeldes angehören. Diese Fläche stellt, ähniich dem Grundwasserspiegel, die theoretische Spiegelfläche des fiuidaien Erdkernes dar.
Der soeben geschilderte Sachverhalt kann wie folgt geometrisch veranschaulicht werden.
Dem archimedischen Prinzip zufolge ist die Masse jedes schwimmenden Körpers gleich jener der verdrängten Flüssigkeit. Denkt man sich also die isostasische Decke der Erde samt ihren Meeresbedeckungen auf die Dichte der fluidaien Unterlage kondensiert, so werden alle durch den Gegensatz zwischen Kontinent und Ozean, Berg und Tal zum Ausdruck gelangenden Unregelmässigkeiten der Erdoberfläche verschwinden und der Erdkörper eine glatte Oberfläche erhalten. Diese Oberfläche, eine Aequiskalarfläche des Gravitations- und Fliehkräftepotentials, ist ein schwach abgepiattetes Rotationsellipsoid, dessen Meridiankurve nach den Ergebnissen des § 35 durch die Gleichung:
| (1) | r = a · (1 - ν · sin2 φ) |
dargestellt ist, worin a den Aequatorradius des Ellipsoides, ν dessen Abplattung und φ die geozentrische Breite bedeutet.
Dieses Ellipsoid kann mit grossem Vorteil bei den nachstehenden Untersuchungen als Bezugssystem benützt werden. Seiner Definition nach ist es nahe verwandt mit dem in der Geodäsie zur Anwendung gelangendem Referenzellipsoid, zu dem man dadurch gelangt, dass man die Fläche des Meeresspiegels durch die Kontinente fortgeführt sich denkt und dabei die ausserhalb desselben befindlichen Massen in das innere zusammengedrängt sich denkt. In unserem Falle erscheint der Meeresspiegel durch die Spiegelfläche des fluidalen Erdkernes ersetzt. Ich werde das durch die Gleichung (1) dargestellte Rotationsellipsoid, zum Unterschied von dem geodätischen Ellipsoid, das geophysikaliche Referenzellipsoid nennen; ich habe es in meinen früheren Schriften als das innere Referenzellipsoid bezeichnet, weil es, wie leicht ersichtlich, innerhalb des geodätischen Referenzellipsoides gelegen ist.
Bezeichnet man mit A, B, C die Trägheitshauptmomente des durch Kondensation der isostasichen Schicht enstandenen Erdkörpers, so wird wegen der vorausgesetzten Homogenität des fluidaien Materials und der axialen Symmetrie der Aequipotentialflächen
| (2) | B = A |
zu setzen sein. Das Trägheitsmoment T bezüglich einer beliebigen durch den Erdmittelpunkt hindurchgehenden Achse ζ kann wie folgt ermittelt werden. Legt man in diesen Mittelpunkt den Ursprung O des orthogonalen Koordinatensystems X = Y = Z, dessen Achse die Trägheitshauptachsen des auf seiner Oberfläche kondensiert gedachten Erdkörpers sind, wozu es wegen der erwähnten axialen Symmetrie nur erforderlich ist, dass die Z-Achse, die wir gegen Norden richten wollen, mit der Rotationsachse des Referenzellipsoides zusammenfällt und bezeichnet mit α, β, γ die Winkel, welche die Achse ζ mit den Koordinatenachsen einschiiesst, so ist das gesuchte Trägheitsmoment nach einem bekannten Satze der Mechanik durch den Ausdruck gegeben:
| (3) |

|
Weil für jede Achse, die mit den Koordinatenachsen die Winkel α, β, γ einschliesst,
| (4) | cos2 α +cos2 β +cos2 γ = 1 |
ist, bekommt man mit Berücksichtigung von (2)

|
d. h.
| (5) |

|
Die Trägheitsmomente sind, wie im zweiten Abschnitt dieses Werkes dargetan, ausschlaggebende dynamische Parameter, weshalb wir ihnen auch im vorliegenden Problem besondere Beachtung schenken müssen. Dabei wird es sich als vorteilhaft erweisen, die den verschiedenen durch O hindurchgehenden Achsen ζ zugeordneten Trägheitsmomente des Erdkörpers auf einer Sphäre abzubilden. Denkt man sich also um den Erdmittelpunkt O eine Kugelfläche mit einem beliebigen Radius beschrieben, dann entspricht jedem Punkte dieser Kugel eine durch diesen Punkt und durch O hindurchgehende Achse ζ und jeder solcher Achse ein bestimmter Wert des Trägheitsmoments T. Auf diese Weise erscheint jedem Punkte der Kugelfläche ein bestimmter Wert von T zugeordnet, so dass diese zu einem sphärischen Feld des Skalars T wird. Dieses Feld ist analytisch durch die Gleichung (5) eindeutig gegeben, geometrisch kann es durch die Aequiskalarlinien, d. h. die Linien des gleichen T veranschaulicht werden. Diese Linien sind durch die Formel
| (6) |

|
gegeben; sie sind Parallelkreise, wenn man die Durchstosspunkte der Achse Z mit der Sphäre als Pole betrachtet.
Kehren wir nun zu dem tatsächlichen Zustand des Erdkörpers zurück, d.h. denken wir uns die kondensiert gedachte isostasische Schale der Erde in ihren wahren Zustand zurückgeführt und fragen wir, welche Aenderungen das soeben geschilderte Feld des Trägheitsmoments T dadurch erleiden wird. Ziehen wir zu die sem Zwecke einen beliebigen Punkt M des geophysikalischen Referenzellipsoides in Betracht. Die Koordinaten dieses Punktes seien r, ψ, φ, wobei r den Radius-Vektor, ψ die von einem beliebigen Meridiane dieses Ellipsoides gezählte Länge und φ, die von der Aequatorebene des Ellipsoides gemessene Breite bedeutet, die in der Richtung gegen Norden positiv zu zählen ist. Begrenzt man an der Stelle M durch die Meridiane ψ und (ψ + dψ) und die Parallelkreise φ und (φ + dφ) ein unendlich kleines Flächenelement df des Referenzellipsoides, so ist
| (7) |

|
Ist D die Mächtigkeit der isostasischen Decke der Erde an der in Betracht gezogenen Stelle und ρ die Dichte des hier befindlichen Materiales, so ruht auf der Fläche df ein vertikales Elementarprisma der isostasichen Decke, dessen Masse durch
| (8) |

|
dargestellt ist. Dieses Prisma taucht so tief in den mit dem Referenzellipsoid begrenzten fluidalen Kern dfr Erde ein, wie es das archimedische Prinzip fordert. Bezeichnet also H die Tauchtiefe des Elementarprismas und ρ, die Dichte der fluidalen Unterlage, so ist die verdrängte Masse derselben gleichρ0 H df und diese muss nach dem archimedischen Prinzip der Masse dμ gleich sein. Es ist also
| (9) |

|
Der Schwerpunkt des auf die Dichte ρ0 kondensiert gedachten Prismas lag ½H oberhalb seiner Basis, jetzt liegt er um ½D von derselben entfernt; die Zurüickführung der isostasischen Schale in ihren natürlichen Zustand hat die Hebung des Schwerpunktes des Elementarprismas um die Strecke
| (10) |

|
zur Folge gehabt. Um diese Strecke liegt der Schwerpunkt S des Elementarprismas oberhalb des Schwerpunktes A der verdrängten fluidalen Masse, welch letzterer Punkt auch der Auftriebspunkt genannt wird. Die Strecke A will ich die isostasische Ueberragung nennen. Diese Strecke ist, wie dies aus den zwei vorstehenden Gleichungen folgt, auch durch durch den Ausdruck
| (11) |

|
veranschaulicht.
Durch diese Hebung des Schwerpunktes der Masse dμ hat sich ihr Trägheitsmoment bezüglich der Achse ζ vergrössert. Diese Aenderung kann wie folgt berechnet werden. Bezeichnet r0 den Radiusvektor des Auftriebspunktes A und θ den Winkel, den dieser Radiusvektor mit der durch den Punkt O hindurchgehenden Achse θ einschliesst, so war das Tr&ä228;gheitsmoment der Masse dθ vor ihrer isostasischen Erhebung und bezüglich der Achse ζ gleich r02 sin2 θ dμ. Nach der Hebung wird das Trägheitsmoment den Wert (r0 + λ)2 sin2 θ d&956; ausweisen, der, weil λ im Vergleich zu r9 sehr klein ist, durch (r02 + 2λr0)sin2 θ dμ ersetzt werden kann. Die Aenderung des Trägheitsmoments, die ich mit dΩ bezeichnen will, ist also gleich:

|
Die Gesamtänderung Ω, die das Trägheitsmoment T durch die isostasische Erhebung der ganzen isostasischen Decke der Erde erfahren hat, wird erhalten, wenn man das über die ganze Erdoberfläche sich erstreckende Integral des vorstehenden Ausdruckes bildet. Dabei kann, weil die Dicke der isostasischen Schichte im Vergleich zu den Abmessungen der Erde sehr klein ist, in der obigen Formel statt r0 der Radiusvektor r des geophysikalischen oder auch jener des geodätischen Referenzellipsoides eingesetzt werden. Aus demselben Grunde braucht auf die Aenderung, die das Gravitationsfeld der Erde durch die isostasische Erhebung erfahren hat, und die nur als eine geringfügige Störung zu betrachten ist, keine Rücksicht genommen werden. Man bekommt also:
| (12) |

|
Um die angegebene Integration durchzuführen, kann der folgende Weg eingeschlagen werden. Das Trägheitsmoment des Elementarprismas dμ der isostasischen Decke ist nach den soeben zugestandenen Vereinfachungen gleich r2 sin2 θ dμ. Man kann deshalb, wie der Vergleich des vorstehenden Ausdruckes mit (12) lehrt, die isostasische Gesamtänderung Ω des Trägheitsmoments T auf die Weise berechnen, dass man jedes Massenelement dμ der isostasischen Decke der Erde mit dem Koeffizient (2λ) ⁄ r behaftet und das Trägheitsmoment der derart reduzierten Massen bezüglich der Achse ζ berechnet. Dies gilt selbstverständlich auch für die Trägheits- und Deviationsmomente bezüglich der Koordinatenachsen X, Y, Z. Die Trägheits- bzw. die Deviationsmomente des elementaren Prismas dμ erfahren also durch die isostasische Erhebung nachstehende Aenderungen:
| (13) |

|
|
| (14) |

|
Diese Ausdrücke erleiden keine Veränderung, wenn man an ihnen die Substitution
| x ∣ — x; y ∣ — y; z ∣ — z |
durchführt, was zu besagen hat, dass die vorstehenden Trägheits- und Deviationsmomente nicht geändert werden, wenn man beliebige Teile der isostasischen Schale der Erde antipodisch verlagert. Aus diesem Grunde ist es bei der Berechnung dieser Momente gestattet, eines Planiglobs der Antipoden sich zu bedienen, wie dies in nachfolgendem geschehen wird.
Führen wir in die vorstehenden Ausdrücke statt der orthogonalen die polaren Koordinaten ein! Der Zusammenhang zwischen diesen beiden Arten von Koordinaten ist durch die Gleichungen gegeben:
| (15) |

|
Benutzt man dies und ausserdem (7) und (8) und setzt der kürzeren Schreibweise halber
| (16) |

|
wo bei gegebenen Abmessungen und Dichteverhältnissen der isostasischen Schale der Erde f(φ, ψ) eine empirisch zu ermittelnde Funktion ist, so bekommt man:
| (17) |

|
| (18) |

|
Durch die über die ganze Erdoberfläche sich erstreckende Integration der vorstehenden Ausdrücke bekommt man die Aenderungen I1, I2, I3, Λ1, Λ2, Λ3, welche die auf die Koordinatenachsen sich beziehenden Trägheits- und Deviationsmomente des ursprünglich auf seiner Oberfläche auf die Dichte ρ0 kondensierten Erdkörpers durch die isostasische Erhebung seiner Decke erfahren haben. Hat man diese Momente ermittelt, so erscheint das vorher definierte Trägheitsmoment Ω bezüglich einer durch den Erdmittelpunkt hindurchgehenden Achse ζ, die mit den Koordinatenachsen die Winkel α, β, γ einschliesst, nach einem bekannten Satze der Mechanik durch den Ausdruck gegeben:
| (19) |

|
Weil
| (20) |

|
ist, bekommt man mit Heranziehung von (15) statt (19) den Ausdruck:
| (21) |

|
wodurch das vorher definierte FeId des Skalars Ω eindeutig gegeben ist.
Durch die vorstehenden Ausführungen ist ein Schema des Erdkörpers gewonnen worden, das die im § 54 mitgeteilten geophysikalischen Tatsachen vollauf berücksichtigt und sich, wie man sehen wird, für die mathematische Behandlung der Polwanderungsfrage gut eignet. Ich will die Grundzüge dieses Schemas hier kurz rekapitulieren. Die Erde, als ein Ganzes aufgefasst, ist als ein fluidaler, d. h. gegen langandauernde Kräfte nachgiebiger Körper zu betrachten, der mit einer unregelmässigen, festen, elastisch biegsamen, vielleicht zerrissenen oder unvollständigen Decke umhüllt ist, die je nach dem Bedarf des hydrostatischen Gleichgewichts in ihre Unterlage teilweise eingetaucht erscheint. Wenn diese Decke auf die Dichte ihrer Unterlage kondensiert wäre, würde die Erdoberfläche vollkommen glatt sein und ein regelmässiges Ellipsoid veranschaulichen, das ich das geophysikalische Ellipsoid benannt habe und das durch die Gleichung (1) dargestellt ist. Die Trägheitshauptmomente des derart kondensiert gedachten Erdkörpers mit A, B, C bezeichnend, wobei B = A ist, und dessen Trägheitshauptachsen als Koordinatenachsen benützend, wäre das Trägheitsmoment des derart gestalteten Erdkörpers in bezug auf eine beliebige durch den Erdmittelpunkt hindurchgehende, mit den Koordinatenachsen die Winkel α, β, γ einschliessenden Achse ζ durch (3) oder (5) gegeben. Die tatsächliche aus dem Referenzellipsoid herausragende Form der isostasischen Decke der Erde hat zur Folge, dass das Trägheitsmoment der Erde bezüglich der Achse ζ nicht gleich T, sondern gleich J ist, wobei
| (22) | J = T + Ω |
ist und Ω durch die vorstehenden Gleichungen gegeben ist. Diese Grösse stellt also den isostasischen Bestandteil des Trägheitsmomentes der Erde dar und ist von grundlegender Bedeutung bei den nachstehenden Untersuchungen.
Kapitel X
Die dynamische Asymmetrie der Erdrinde und ihre Folgen
§ 56. Die Anomalie der Trägheitspole des Erdkörpers. Durch die vorstehenden Ergebnisse ist das Trägheitsmoment J des Erdkörpers, d.h. seines fluidalen Kerns, seiner isostasischen Hülle und ihrer Wasserbedeckungen bezüglich einer beliebigen durch den Erdmittelpunkt hindurchgehenden Achse ζ eindeutig gegeben. Dadurch ist man in die Lage versetzt, auch die Lage der Trägheitshauptachsen des Erdkörpers zu ermitteln, in bezug auf welche das Trägheitsmoment J seine extremen Werte erreicht. Die der Drehachse der Erde benachbarte Trägheitshauptachse, die dem maximalen Wert des Trägheitsmoments J entspricht, trifft die Erdoberfläche in zwei Punkten, die man als Trägheitspole der Erde zu bezeichnen pflegt. Weil ich das geophysikaliche Referenzellipsoid als Bezugssystem benütze, will ich die Durchstosspunkte der erwähnten Trägheitshauptachse mit diesem Ellipsoid als die Trägheitspole des Erdkörpers bezeichnen. Es sei dabei P der nördliche, P′ der südliche Trägheitspol der Erde. Die Achse des Referenzellipsoides, die mit der Z-Achse des Koordinatensystems X-Y-Z zusammenfallend angenommen war, trifft die Oberfläche des Referenzellipsoides in zwei Punkten, die ich die Referenzpole nennen will; der nördliche dieser beiden Pole sei mit F, der südliche mit F′ bezeichnet.
Wegen der Isostasie der Erdrinde fallen, wie sogleich gezeigt werden wird, die Trägheitspole mit den Referenzpolen nicht zusammen, können aber von diesen, weil die isostasische Rinde im Verhältnis zu den Erdabmessungen sehr dünn ist, nur ganz wenig entfernt sein. Um die Lage der Trägheitspole - es genügt nur den nördlichen dieser beiden Pole in Betracht zu ziehen - in bezug auf die Referenzpole zu ermitteln, lasse man die vostehend definierte Sphäre, auf der das Trägheitsmoment J abgebildet erscheint und deren Mittelpunkt im Erdmittelpunkt gelegen ist, durch die Referenzpole hindurchgehen, lege durch den nördlichen Referenzpol F eine Tangentialebene an das Referenzellipsoid und jene Sphäre und fixiere in dieser Ebene ein orthogonales Koordinatensystemξ-η, dessen Ursprung im Punkte F gelegen ist. Jedem Punkte des sehr kleinen Bereiches dieser Sphäre, der hier in Betracht kommt, und der durch ihre Tangentialebene ersetzt werden kann, entspricht eine bestimmte durch den Erdmittelpunkt hindurchgehende Achse ζ und dieser ein bestimmter Wert des Trägheitsmomentes J des Erdkörpers. Der gesuchten Trägheitshauptachse bzw. dem gesuchten Trägheitspol entspricht der maximale Wert von J, weshalb seine Lage aus den Gleichungen:

|
zu ermitteln ist. Man bekommt also mit Rücksicht auf (22) die folgenden für die Ermittlung des Trägheitspoles dienenden Gleichungen:
| (23) |

|
Weil sich der Trägheitspol T in der nächsten Nähe des Referenzpoles F, also in jener des Ursprunges unseres Koordinatensystems ξ-η befindet, sind dessen Koordinaten, die wir nach dem Winkel, den der Radiusvektor der zugehörigen Punkte der Achse ξ bzw. η mit der Z-Achse einschliesst, in Bogenmass messen wollen, sehr klein. Man bekommt also, wenn man die in (23) vorkommenden Funktionen T und Ω in Maclaurinsche Reihen entwickelt und die höheren Potenzen von ξ und η wegen ihrer Kleinheit vernachlässigt, die nachstehenden Gleichungen:
| (24) |

|
Es folgt aus (5)
| (25) |

|
Weil vom Ursprung F des Koordinatensystems ξ-η, also von der Z-Achse gemessen, die Bogendifferentiale dξ und dη dasselbe darstellen, was dγ ist, so wird wegen (25)

|
Berücksichtigt man überdies, was sich bei der späteren numerischen Berechnung ergeben wird, dass die Grössen ∂2Ω ⁄ ∂ξ2, ∂2Ω ⁄ ∂θ2 im Vergleich zu 2(C-A) sehr klein sind, also vernachlässigt werden können, so bekommt man statt (24) die Gleichungen:
| (26) |

|
durch die die Lage des Trägheitspoles in bezug auf den Referenzpol dargestellt ist.
Durch die Gleichung (21) war das Feld Ω(φ, ψ) des Skalars Ω auf der oben angegebenen Sphäre abgebildet. Geht man zwecks Abbildung des sehr kleinen um den Referenzpol gelegenen Bereiches des Skalars Ω von der Sphäre auf ihre Tangentialebene über und richtet die Achse ξ des dabei benützten Koordinatensystems ξ-η derart, dass sie den nullten Meridian tangiert, so erhält man die Schnittlinie des Feldes Ω(φ, ψ) mit der ξ-Achse, wenn man in (21) ψ = 0; φ = π ⁄ 2 - ξ setzt. Diese Schnittlinie ist also durch die Gleichung gegeben:

|
Die Schnittlinie des Feldes Ω(φ, ψ) mit der η-Achse wird erhalten, wenn man in (21) ψ = π ⁄ 2; φ = π ⁄ 2 - ηsetzt; sie ist also durch die Gleichung gegeben:

|
Es ist deshalb

|
d. h.

|
Setzt man dies in (26) ein, so bekommt man:

|
Dies sind die Koordinaten des Trägheitspoles des Erdkörpers in bezug auf den Referenzpol; ich will sie mit a1 und a2 bezeichnen. Es ist also
| (27) |

|
Der absolute Betrag der in Bogenmass gemessenen Entfernung des Trägheitspoles vom Referenzpole ist gleich:
| (28) |

|
Diese Grösse will ich die Anomalie des Trägheitspoles nennen; sie kann nur dann Null werden, wenn Λ1 und Λ2 zugleich Null sind, d. h. wenn die Achse des Referenzellipsoides die Hauptachse des isostasischen Bestandteiles des Trägheitsmomentes der Erde ist. Dies ist nur bei einer ganz besonderen Lage der isostasischen Decke der Erde auf derem fluidalen Kern möglich, sonst hat die Anomalie des Trägheitspoles immer einen endlichen Wert. Durch dieses Ergebnis gelangt die dynamische Asymmetrie des Erdkörpers zum deutlichen, mathematisch erfassten Ausdruck. Der im § 53 bereits erwähnte Löffelholz von Colberg, ein ehemaliger österreichischer Artillerieoffizier, hat aus der gewaltigen Erhebung der Kontinente über dem Meeresspiegel mit genialer Intuition auf eine solche Asymmetrie geschlossen, war aber nicht in der Lage, diese mathematisch zu erfassen und für das Rotationsproblem der Erde zu verwerten. Diese Anomalie spielt die Rolle der Triebfeder im Mechanismus der Polwanderungen.
§ 57. Die dynamische Anpassung des Erdkörpers. Wie im § 36 gezeigt, erfolgt die kräftefreie Drehbewegung der Erde derart, dass der Rotationspol der Erde während der Periode T, die je nachdem man den Erdkörper als starr oder als elastisch annimmt, eine Dauer von 305 bzw. 430 Sterntagen aufweist, einen vollen Umlauf auf seiner kreisförmigen um den Trägheitspol geschlungenen Bahn vollführt. Weil es sich jetzt um die Erforschung der säkularen Verlagerungen des Rotationspoles handelt, kann diese ganz unbedeutende kurzperiodische Bewegung ausser Acht gelassen werden, indem man dem Rotationspole seine mittlere der erwähnten Periode entsprechende Lage zuweist. Diese mittlere Lage ist aber, weil die Bahnkurve des Rotationspoles um den Trägheitspol ein Kreis ist, der Trägheitspo1 selbst. Dieser mittlere Rotationspol weist nach den Ergebnissen des vorhergehenden Paragraphen einen endlichen Abstand vom Referenzpol auf. Dieser Umstand wird zu Folge haben, dass der mit dem Referenzellipsoid begrenzte fluidale Erdkern deformierenden Kräften ausgesetzt sein wird und diesen mit der Zeit auch nachgeben wird, seine isostasische Decke in Mitleidenschaft ziehend. Dieser Vorgang, auch Anpassung des Erdkörpers genannt, kann auf die einfachste Weise mathematisch wie folgt beschrieben werden, wobei wir unsere Betrachtungen auf jenen Meridianschnitt des Referenzellipsoides beschränken wollen, in dem der erwähnte mittlere Drehpol der Erde gelegen ist, weil in diesem Meridianschnitt die deformierenden Kräfte ihren Grösstwert erreichen. Weil infolge seiner Anpassung der Erdkörper seine Form langsam aber ständig ändert, soll den nachstehenden Betrachtungen ein beliebiger Zeitpunkt t der Erdgeschichte als Ausgangspunkt gewählt werden.

Seien in der Fig. 23 die dem Zeitpunkt t entsprechenden dynamischen Verhältnisse veranschaulicht. AA′ und FF′ seien die Hauptachsen des den Referenzpol F und den mittleren Drehpol P enthaltenden Meridianschnittes des Referenzellipsoides. Die Polargleichung dieses Meridianschnittes ist die eingangs mitgeteilte Gleichung (1).
Die Kräftefunktion der Graviations- und Fliehkräfte des Erdkörpers ist durch den Ausdruck (125) des zweiten Abschnittes dieses Buches veranschaulicht, wobei das zugehörige Koordinatensystem X-Y-Z mit den Hauptachsen des Referenzellipsoides zusammenfallend angenommen worden ist, auf welches sich auch die Gleichung (1) bezieht. Im vorliegenden Falle fällt die Drehachse des Erdkörpers nicht mit der Z-Achse zusammen, sondern schliesst mit derselben den im vorigen Paragraphen ermittelten Winkel α ein. Aus diesem Grunde wird das letzte, die Funktion der Fliehkräfte darstellende Glied des Ausdruckes (125), welches, wenn man statt der geozentrischen Breite deren Komplement, die Poldistanz δ = π ⁄ 2 - φ einführt, durch den Ausdruck (n2r2 ⁄ 2) · sin2 δ dargestellt ist, infolge der bestehenden Anomalie α eine Aenderung erfahren, die durch

|
dargestellt sein wird, weil sich die Poldistanz δ des Punktes M, die in der Richtung PF vom Referenzpole zu messen ist, um den sehr kleinen Winkel α vergrössert hat und weil die zugehörige Aenderung des Radiusvektors r nicht im Betracht gezogen werden muss. Es ist also
| (29) |

|
Durch diese Aenderung der Kräftefunktion wird eine auf die im Punkte M des Referenzellipsoides befindliche Masseneinheit wirkende Kraft 𝕽 erzeugt. Grässe und Richtung dieser Kraft können wie folgt ermittelt werden. Weil diese Kraft in dem in Betracht gezogenen Meridianschnitt gelegen ist, kann sie in eine in die Richtung des wachsenden r und eine darauf senkrechte gegen den Aequator gerichtete Komponente zerlegt werden. Bezeichnet man diese Komponenten mit V bzw. H, so ist

|
wobei das Element ∂n der Normalen auf r durch ∂n = r∂δ ersetzt werden kann, so dass es ist:

|
Man bekommt also mit Benützung von (29):
| (30) |

|
Die durch die Anomalie des Trägheitspoles hervorgerufenen Fliehkräfte werden das Bestreben haben, den fluidalen Erdkern zu deformieren. Die Art und Weise dieser Deformation ist aus den vorstehenden Gleichungen sofort ersichtlich. Weil, wie angegeben, die Poldistanz δ von der Achse OF aus in dem dem Umlauf des Uhrzeigers entgegengesetzten Sinne von 0° bis 360° zu messen ist, so ist im ersten und und dritten Quadranten, denen die Teile FA und F′A′ des in Fig. 23 dargestellten Meridianschnittes des Referenzellipsoides angehören, nach (30) die Vertikalkomponente V der Kraft 𝕽 positiv, weshalb diese Kraft nach oben gerichtet ist und das Bestreben haben wird, am Referenzellipsoid Ausbuchtungen zu erzeugen; im zweiten und vierten Quadrant, denen die Teile AF′ und A′F des Meridianschnittes angehören, ist diese Kraft nach unten gerichtet und wird das Bestreben haben das Ellipsoid einzudrücken. Der Erdkörper wird, weil er sich um die Rotationsachse OP dreht, jener Gleichgewichtsform zustreben, die nach dem Clairaut′schen Theorem ein Rotationsellipsoid mit der Achse OP ist, dessen Meridianschnit in der Fig. 23 durch die mit ihren Achsen A1A1′ und F1F1′ gekennzeichnete Ellipse ist. Dadurch wird der Refereenzpol nach und nach aus der Lage F in die Lage F1 gelangen. Um die Frage beantworten zu kennen, wie sich durch diesen Vorgang die Lage des Referenzpoles in bezug auf die Erdrinde verändert hat, muss vorher untersucht werden, welche Folgen die soeben geschilderte Anpassung des fluidalen Erdkernes auf seine isostasische Hülle und ihre Lage auf demselben haben müsse. Ziehen wir zu diesem Zwecke das vor der Anpassung an der Stelle M des Referenzellipsoides befindliche elementare Teilchen der isostasischen Decke der Erde in Betracht. Die Anpassung wird dieses Teilchen in der Richtung der Kraft 𝕽 verschieben, bis es im Punkte M1 der dem neuen Gleichgewichtszustand angepassten Oberfläche des Referenzellipsoides seine Endlage erreichen wird. Um diese Lage in bezug auf den ursprünglichen und den neuen Referenzpo1 zu ermitteln, beschreibe man mit dem Radius OM den Bogen MT, dessen Zentriwinke1 MOT gleich ist der Anomalie α des Trägheitspoles. Um diesen Winkel erscheint die ursprüngliche Meridiankurve des Referenzellipsoides nach rechts gedreht, so dass die neue Meridiankurve durch den Punkt T hindurchgehen muss. Weil der Bogen MT wegen der Kleinheit des Winkels α sehr klein ist, kann er durch die auf OM senkrecht stehende gerade Strecke MT ersetzt werden. Ersetzt man den ebenfalls sehr kurzen Bogen TM1 der Meridianellipse durch die im Punkte T an die Meridianellipse gezogene Tangente, so bekommt man das in Fig. 24 abgebildete Dreieck MTM1.

In demselben stellt der Winkel MTM1, der mit τ1 bezeichnet werden möge, jenen Winke1 dar, den die Tangente der Meridianellipse mit der auf dem zugehörigen Radiusvektor errichteten Normalen einschliesst. Die Gleichung dieser Ellipse ist durch (1) veranschaulicht. Der Winkel τ, den die Tangente dieser Ellipse mit dem Radiusvector einschliesst, ist durch die für alle ebene Kurven gültige Gleichung:

|
gegeben, worin r′ die Ableitung des Radiusvektors r nach der Amplitude bedeutet. Der Winkel τ1, den die Tangente mit der Normalen des Radiusvektors einschliesst, ist gleich dem Komplement des Winkels τ, weshalb
| (31) |

|
ist. Zieht man die Gleichung (1) heran und führt in dieselbe als Amplitude statt der geozentrischen Breite φ die Poldistanz δ = π &frasl: 2 - φ ein, so wird:
| (32) |

|
Es ist deshalb
| (33) |

|
Verlängert man TM bis zum Fusspunkt N der auf diese Strecke aus M1 gefällten Normalen, dann stellen NM1 bzw. MN die beiden Komponenten der Verrückung MM1 dar, die erstere, die mit Δh bezeichnet werden möge, veranschaulicht die Verrückung in der Richtung des Radiusvektors r, die zweite, die mit Δξ bezeichnet und in Bogensmass gemessen werden soll, stellt die Verrückung in der auf dem Radiusvektor senkrechten Richtung dar. Dieselbe Richtungen weisen die Komponenten V und H der Kraft 𝕽 auf. Bezeichnet man also den Winkel NMM1 mit β so ist
| (34) |

|
Setzt man in diese Gleichung die Ausdrücke (30) ein, so wird
| (35) |

|
d. h.
| (36) |

|
Es folgt aus dem Dreieck NMM1, in dem NM1 gleich Δh und NM gleich rΔξ ist, weil Δξ in Bogenmass gemessen war,

|
und aus dem Dreieck NMT1, weil MT = rα ist,

|
Löst man diese Gleichungen nach Δξ und Δh auf, so wird
| (37) |

|
Setzt man in diese Formeln die Ausdrücke (33) und (35) ein, so sind die gesuchten Komponenten der Verrückung gefunden. Dabei ist folgendes zu beachten. Die Abplattung ν des geophysikalischen Referenzellipsoides kann sich, weil die isostasische Decke der Erde sehr dünn ist, nur wenig von der Abplattung des geodätischen Ellipsoides unterscheiden, für die im § 35 der Wert ν = 1 ⁄ 298 angegeben worden ist. Deshalb kann im Nenner des Ausdruckes (33) das Glied ν cos2 δ neben der dort auftretenden Einheit vernachlässigt werden. Auf diese Weise bekommt man:

|
Man kann auch hier das Glied ν cos 2δ neben der Einheit unterdrücken und man bekommt schliesslich:
| (38) |

|
Dabei erscheint Δξ im Bogenmass Δh in linearem Mass gemessen.
Diese Verrückungen des Punktes M der isostasischen Decke der Erde betreffen nur jenen Meridianschnitt des Referenzellipsoides, in welchem der Drehpol der Erde gelegen ist; ausserhalb dieses Meridianes werden sie immer kleiner, um in sekrecht stehendem Meridiane gänzlich zu verschwinden. Diese Verrückungen sind also Funktionen der geographischen Koordinaten φ und ψ oder, falls man sich auf den erwähnten Hauptschnitt beschränkt, Funktionen der Poldistanz δ. Gemäss den durch die Fig. 23 festgelegten Bezeichnungen sollen die Grössen α und δ in entgegengesetzter Richtung gezählt werden, so dass der Rotationspol P im vierten Quadrant von δ, knapp vor dem Werte δ = 360° anzunehmen ist.
Die vertikale Verrückung Δh ist gleich der an der betreffenden Stelle stattgefundenen durch die Deformation des fluidalen Erdkernes hervogerufenen Erhebung der Spiegelfläche dieses Kernes, denn diese ist, weil sich diese Spiegelfläche um δ = α gedreht hat, nach (32) durch

|
oder, falls man in (32), wie es oben geschehen ist, ν cos2 δ neben der Einheit unterdrückt, durch

|
veranschaulicht, so dass Δh1 = Δh ist.
Die horizontale Verrückung Δψ des Punktes M der isostasischen Decke ist eine Funktion der Poldistanz δ; sie ist positiv, also der der Bewegung des Uhrzeigers entgegengesetzten Richtung, für die Intervalle δ = 0 bis δ = 45°; δ = 135° bis δ = 225°; δ = 315° bis δ = 360°, sonst ist sie negativ, wie dies durch die Fig. 25 veranschaulicht erscheint. In den mit einem Ring gekennzeichneten Punkten, in welchen ein Richtungswechsel der Verrückung stattfindet, ist sie gleich Null.

Diese horizontale Verrückung ist selbst an jenen Stellen, wo sie ihre extremen Werte να oder -να erreicht, wegen des Faktors ν sehr klein. Während sich also der Referenzpol um die in Bogenmass gemessene Strecke FF1 = α verlagert hat, hat sich der Punkt M höchstens nur um den dreihundertsten Teil jener Verrückung verschoben. Diese Verrückung ist gegenüber jener Verlagerung sehr klein, so dass gesagt werden kann, der Anpassungsvorgang ändert die horizontale Konfiguration der isostasischen Decke nur unmerklich; unter derselben gleitet der Referenzpol nach Massgabe der Anomalie α. Ist er durch den soeben geschilderten Anpassungsvorgang aus der Stellung F in Stellung F1 angelangt, so wird dieser neuen Lage des Referenzpoles in bezug auf die iscstasische Decke der Erde ein neuer Wert α1 der Anomalie des Trägheitspoles entsprechen, also eine neue Lage P1 des mittleren Rotationspoles. Infolgedessen wird eine neue Anpassung des Erdkörpers an die neue Lage des Drehpoles beginnen. Dieser Anpassungsvorgang kann nur dann zum Stillstand gelangen, wenn die durch (28) dargestellte Anomalie gleich Null wird, d. h. wenn der Rotationspol auf seinem Weg den Trägheitspol des Feldes Ω erreicht hat.
Dieser Vorgang wird im nachstehenden Kapitel seine mathematische Beschreibung erfahren, vorher will ich über die in der isostasischen Decke der Erde durch den Anpassungsvorgang hervorgerufenen Spannungen kurz berichten, wobei ich mich auch diesmal auf den erwähnten Meridianschnitt der maximalen Spannungen beschränken will.
An der Stelle M, der eine Poldistanz δ entspricht, erfährt der dort befindliche Teil der isostasischen Decke der Erde eine Horizontalverschiebung, die in Längenmass gemessen

|
beträgt. Unmittelbar daneben, in der horizontalen Entfernung l = r dδ, erfährt die Decke die Verschiebung:

|
Die Gesamtdehnung Δl der Länge l beträgt also

|
Weil nach dem Hooke′schen Gesetz

|
ist, worin σ die Zugspannung und E den Elastizitätsmodul des Materials bedeutet, so wird
| (39) |

|
Diese Spannung erreicht ihre extremen Werte 2 ν α E bzw. -2 ν α E an der Poldistanz δ = 135° und δ = 315° bzw. an der Poldistanz δ = 45° und δ = 225°; sie sind der Abplattung des Referenzellipsoides, dem Elastizitätsmodul des Materials und der Anomalie des Trägheitspoles direkt proportional.
Kapitel XI
Der Mechanismus der säkularen Polwanderungen
§ 58. Die vektorielle Grundgleichung der säkularen Bewegung der Erdpole. Im vorhergehenden Kapitel habe ich, um alle hier in Betracht zu ziehenden Eigentümlichkeiten des Baues der Erde und ihrer Rinde mathematisch beschreiben zu können, das geophysikalische Referenzellipsoid als Bezugssystem benutzt. Nachdem auf diese Weise die erforderlichen Schlussfolgerungen hinsichtlich der Trägheitsmomente des Erdkernes und seiner isostasischen Hülle gezogen und für die weitere Behandlung des Problems der Polverlagerungen vorbereitet worden sind, kann ich nun die Erdoberfläche selbst als Bezugssystem benützen und dabei, weil die Abplattung der Erde und die Unregelmässigkeiten ihrer Rinde in den Trägheitsmomenten T und Ω, die als dynamische Parameter bei der Drehbewegung der Erde allein in Betracht kommen, bereits zum Ausdruck gekommen sind, die Erdoberfläche, unter der das mittlere Niveau der Meere zu verstehen ist, als kugelförmig voraussetzen. Diese Kugelfläche möge zu gleicher Zeit zur Abbildung des sphärischen Feldes der Trägheitsmomente T und Ω benützt werden.
Die soeben zugestandenen Vereinfachurigen beeinträchtigen die Genauigkeit der Berechnung der Polbahnkurven ganz unwesentlich; die durch sich ergebenden geringen Abweichungen fallen auch deshalb nicht in die Wagschale, weil wir nicht in der Lage sind, genaue Angaben über die Mächtigkeit der isostasischen Decke der Erde zu machen.
Ich nehme also bei den nachstehenden Ausführungen an, die Erde sei kugelförmig, weil ihre aus der Abplattung und aus der Unregelmässigkeit ihrer Rinde sich ergebenden dynamischen Eigentümlichkeiten durch die Trägheitsmomente T und Ω bereits zum richtigen Ausdruck gebracht worden sind. Daraus ergibt sich das folgende.
Denkt man sich die Achse des geophysikalischen Referenzellipsoides gegen Norden verlängert, so trifft dieselbe die Erdoberfläche in einem Punkte F, den ich den nördlichen Figurenpol der Erde nennen will. Sieht man von der ganz gering fügigen freien Nutation der Erde ab, so trifft die Drehachse der Erde deren nördliche Hemisphäre in einem Punkte, der mit dem nördlichen Trägheitspol P der Erde zusammenfällt. Die gegenseitige Entfernung der beiden Punkle F und P ist sehr klein und man kann jenen Bereich der Erdoberfläche, in dem diese Punkte liegen und auf dem sich die nachstehenden Betrachtungen beziehen, als eben betrachten. Fixiert man in diesem ebenen Bereich ein mit der Erdrinde fest verbundenes orthogonales Kordinatensystem ξ—η, dessen Ursprung, wofern er dem erwähnten Bereich angehört, beliebig gewählt werden kann, so sind die beiden in die Achsen dieses Koordinatensystems fallenden Projektionen der in Bogenmass zu messenden Strecke FP nach (26) durch die Ausdrücke gegeben:
| (40) |

|
in welchen sich die partiellen Ableitungen auf den Punkt F beziehen. Der Ortsvektor 𝖆 des Punktes P in bezug auf den Punkt F ist also durch den Ausdruck
| (41) |

|
veranschaulicht, in dem 𝖎 und 𝖏 die Einheitsvektoren der Achsenrichtungen ξ und η bedeuten. Setzt man (40) in (41) ein, so wird

|
d. h.
| (42) |

|
Dieser Ausdruck stellt uns vektoranalytisch die Anomalie des Trägheitspoles dar, die nach den Ausführungen des § 57 die Ursache des Anpassungsvorganges ist. Durch diese Anpassung wird, wie dort geschildert, der Punkt F in bezug auf die Erdrinde, also in bezug auf das Koordinatensystem ξ—η in der Richtung des Vektors 𝖆 gegen den Punkt P wandern, wodurch die Richtung seiner Bewegung, also die Richtung seines Geschwindigkeitsvektors 𝖛 gegeben ist. Weil nach (30) die die Anpassung hervorrufenden Kräfte dem Betrag α der Anomalie 𝖆 proportional sind und weil die Anpassungen langsam und mit Ueberwindung der Viskosität des Erdkernes vor sich geht, muss ihre Aupassungsgeschwindigkeit, also auch die skalare Grösse der Geschwindigkeit 𝖛 der Anomalie α proportional sein Daraus folgt:
| (43) | 𝖛 = κ · 𝖆 |
worin κ einen konstanten Faktor bedeutet, der der Anpassungskoeffizient des Erdkörpers genannt wird. Mit dieser Geschwindigkett sich bewegend, würde der Figurenpol F mit dem Trägheitspol zur Koinzidenz gelangen, wenn dadurch die Anomalie 𝖆 verschwinden würde. Aber diese kleine, aber endliche Grösse, die eine Funktion der Lage des Punktes F ist, kann nach (42) nur dann gleich Null werden, wenn der Gradient des skalaren Feldes Ω Null wird, und dies ist nur an jenen Stellen der Erdoberfläche möglich, in denen die Hauptachsen des Tensors Ω die Erdoberfläche durchdringen. Solange der Figurenpol F einen dieser Punkte nicht erreicht hat, wird er sich verlagern und den Trägheitspol vor sich schieben in der Richtung der Anomalie 𝖆, die der jeweiligen Lage des Punktes F auf der Erdoberfläche zugeordnet erscheint. Die beiden Punkte F und P werden sich also in einer sehr kleinen gegenseitigen Entfernung α in der Richtung des Vektors 𝖆; und mit einer Geschwindigkeit 𝖋, die diesem Vektor proportional ist, einer hinter dem anderen auf der Erdoberfläche bewegen, bis sie endlich ihre gemeinsame Gleichgewichtslage, in der 𝖆 = 0 ist, erreicht haben werden. Der Ausdruck (43) stellt also die Geschwindigkeit der gemeinsamen Bewegung dieser zwei Punkte in bezug auf die feste Erdoberfläche dar. Weil, wie im vorigen Paragraphen gezeigt, der mittlere Drehpol der Erde mit dem Trägheilspol zusammenfällt, stellt uns die Grösse 𝖛 die Geschwindigkeit der Bewegung des mittleren Drehpoles, also der säkularen Bewegung des Rotationspoles der Erde in bezug auf die Erdoberfläche dar.
Es folgt aus (42) und (43), wenn der kürzeren Schreibweise halber gesetzt wird,
| (44) |

|
worin n eine Konstante bedeutet, als Endergebnis der vorstehenden Betrachtungen:
| (45) | 𝖛 = n · grad Ω |
Dies ist die vektorielle Grundgleichung der säkularen Polbewegung.
Aus der Gleichung (45) folgt das grundlegende Theorem hinsichtlich der säkularen Polbewegung:
Der Geschwindigkeitsvektor der säkularen Polbewegung ist in jedem Punkte der Polbahn proportional dem Gradient des Feldes Ω.
Dieses Theorem kann wie folgt geometrisch gedeutet werden. Weil der Geschwindigkeitsvektor 𝖛 der säkularen Polbewegung auch die Tangente der Polbahn veranschaulicht und in jedem Punkte dieser Bahn mit dem Gradient von Ω zusammenfällt, ist die Bahnkurve des Drehpoles eine der Vektorlinien des Feldes grad Ω. Welche von diesen Linien die tatsächliche Bahnkurve des Poles veranschaulicht, ist durch die gegenwärtige Lage des Drehpoles, durch die ein Punkt der Polbahn gegeben ist, eindeutig beantwortet.
Nach einer allgemeinen Eigenschaft des Gradienten kreuzen die Vektorlinien des Feldes grad Ω unter geradem Winkel die Linien des gleichen Ω, sind also orthogonale Trajektorien der Linien gleichen Trägheitsmomentes Ω. Daraus ergibt sich das folgende geometrische Bild der Polwanderungen. Um zu ihrer stabilen Lage zu gelangen, muss die auf dem fluidalen Erdkern isostasisch gelagerte Decke der Erde so lange die anpassenden Deformationen des Erdkernes mitmachen, bis der Trägheitspol des Feldes Ω mit dem Figurenpol der Erde zusammenfällt. Bei dieser Bewegung verzeichnet der Drehpol auf der Erdrinde eine Linie, die mit der Fall-Linie einer topographischen Fläche verglichen werden kann. So wie diese Fall-Linie die Schichtenlinien der topographischen Fläche, d. h die Linien des gleichen Schwerkraftpotentials, senkrecht kreuzt, so verläuft die Polbahnkurve senkrecht zu den Linien des gleichen Trägheitsmomentes Ω. Anders gesprochen: die Erdrinde fällt relativ zum Drehpol nach der Linie des steilsten Gefälles von Ω. Aus dieser jetzt leicht verständlichen Eigenschaft der Polbahnkurve foIgen alle ihre weitere Eigenschaften und diese Kurve selbst; sie zu finden ist jetzt ein rein geometrisches Problem.
§ 59. Periodische Glieder der Polbahnbewegung.
§ 60. Eine andere Ableitung der Grundglelchung der säkularen Bewegung der Erdpole. Sehr bald nachdem ich die im § 58 mitgeteilte Grundgleichung abgeleitet und veröffentlich hatte, gelang es mir, eine andere Ableitung dieser Grundgleichung zu finden, die wegen ihrer Einfachheit und Anschaulichkeit den Beifall der Geophysiker fand und die hier wiedergegeben werden möge.
Die Kräftefunktion des Gravitations- und Fliehkraftfeldes der Erde ist nach der Gleichung (125) des zweiten Abschnittes dieses Buches durch den Ausdruck
| (73) |

|
veranschaulicht.
Zieht man das an einer beliebigen Stelle der Erdoberfläche befindliche, im § 55 gekennzeichnete Elementarprisma der isostasischen Decke der Erde in Betracht, so ergibt sich folgendes. Dieses Prisma taucht in den fluidalen Erdkern hinein und seine Tauchtiefe ist gleich H. Der Schwerpunkt M des verdrängten fluidalen Materials, der auch der Auftriebspunkt genannt wird, liegt in der Mitte der Tauchtiefe H, der Schwerpunkt S des Elementarprismas liegt in der Mitte der Höhe D dieses Prismas, der Höhenunterschied λ dieser beiden Punkte, die isostasische Erhebung, ist durch den Ausdruck (11) veranschaulicht. Die Masse dμ des Elementarprismas kann in derem Schwerpunkt konzentriert gedacht werden. Die auf das Elementarprisma einwirkende Kraft ist gleich dem Gradient von W im Punkte S multipliziert mit der Masse dμ. Diese Kraft weist, wie sofort gezeigt werden wird, eine in bezug auf die durch M hindurchgehende äquiskalare Fläche des Feldes W tangentielle Komponente auf, die auf folgende Weise ermittelt werden kann.

Seien PP′ (Fig. 27, Seite 243) die beiden Drehpole der Erde und PMP′ der durch den Punkt M hindurchgehende Meridian der Erdoberfläche. Legt man in den Punkt M den Ursprung des orthogonalen in der Meridianebene liegenden Koordinatensystems x-y, dessen y-Achse vertikal nach oben und dessen x Achse gegen den Aequator gerichtet ist, so ist für diesen Punkt:
| (74) |

|
weil in demselben die x-Achse die Aequiskalarfläche des Feldes W berührt. Der Punkt S weist in bezug auf das Koordinatensystem x-y die Koordinaten x = 0; y = λ auf. In diesem Punkte wird die partielle Ableitung von W nach x nicht gleich Null, sondern durch den Ausdruck
| (74a) |

|
veranschaulicht sein, worin sich die darin vorkommenden Ableitungen auf den Punkt M beziehen. Deshalb wird mit Rücksicht auf (74) die auf das Elementarprisma dμ einwirkende Horizontalkraft durch den Ausdruck
| (75) |

|
dargestellt sein.
Verlauscht man, was zulässig ist, die Reihenfolge der obigen Ableitungen, so wird:
| (76) |

|
Die Ableitung
| (77) |

|
stellt die Schwerebeschleunigung im Punkte M dar; diese Beschleunigung ist nach abwärts gerichtet, weshalb in obiger Gleichung das Zeichen Minus gesetzt werden musste. Setzt man (77) in (76), so bekommt man:
| (78) |

|
In dieser Formel kann für das Element ∂x der Meridiantangente der Ausdruck
| (79) |

|
eingesetzt werden, in dem, weil die geozentrische Breite φ entgegengesetzt der Richtung x zunehmend ist, rechts das Zeichen Minus vorkommt. Man bekommt also:
| (80) |

|
Die Abhängigkeit der Schwerebeschleunigung von der geozentrischen Breite φ ist durch die Formel (136) des zweiten Abschnittes dieses Buches, d. h. durch
| (81) |

|
gegeben, worin ga die Schwerebeschleunigung am Aequator, gp jene an den Polen bedeutet. Setzt man dies in (80) ein, so wird:
| (82) |

|
Diese Kraft, in der Meridianebene wirkend, ist, weil gp > ga und die x-Achse des hier benützten Koordinatensystems gegen den Aequator gerichtet ist, ebenfalls gegen den Aequator gerichtet, weshalb sie auch den Namen Polfluchtkraft erhalten hat. Bei gleichbleibendem λ würde sie ihr Maximum an der Breite φ = 45° erreichen. An den Polen und am Aequator ist sie gleich Null.
Jedes Elementarprisma der aus dem fluidalen Kern herausragenden isostasischen Decke der Erde unterliegt einer solchen horizontalen Kraft, und es ist unsere nächste Aufgabe, das Drehmoment aller dieser Kräfte zu berechnen. Dabei können wir, weil aus der ellipsoidalen Gestalt der Erde und jener der Aequiskalarflächen des zugehörigen Kraftfeldes alle Konsequenzen bereits gezogen sind, die Erdoberfläche als kugelförmig betrachten und in den vorstehenden Gleichungen für r den mittleren Radius r0 der Erde setzen. Unter dieser Voraussetzung wird das Drehmoment der Kraft dH in bezug auf den Erdmittelpunkt die skalare Grösse
| (83) |

|
aufweisen.
Um dieses Drehmoment, wie es sich als notwendig ergeben wird, vektoranalytisch darzustellen, lege man (Fig. 27) in den Erdmittelpunkt den Ursprung O eines orthogonalen Koordinatensystems X-Y-Z, dessen Z-Achse, mit der Drechachse der Erde zusammenfallend, gegen Norden gerichtet werden möge; die Y-Achse falle in die die in Betracht gezogene Elementarmasse dμ enthaltende Meridianebene der Erde. Bezeichnet man mit 𝕾, 𝕿, 𝖀 die Einheitsvektoren der Achsenrichtungen des Koordinatensystems X-Y-Z, so ist, weil der Einheitsvektor 𝕾 senkrecht auf der erwähnten Meridianebene steht und das Drehmoment als positiv zu bezeichnen ist, wenn es entgegengesetzt dem Umlaufssinne des Uhrzeigers wirkt, das Drehmoment d𝕸 der auf die Elementarmasse dμ einwirkenden Horizontalkraft durch den Ausdruck:
| (84) |

|
veranschaulicht. Setzt man hier (82) mit r = r0 ein, so bekommt man:
| (85) |

|
Ich habe im § 55 die durch die isostasische Erhebung λ der Masse dμ hervorgerufene Aenderung des Trägheitsmometltes der Erde bezüglich der mit dem Radiusvektor r den Winkel θ einschliessenden durch den Erdmittelpunkt hindurchgehenden Achse ζ mit dΩ bezeichnet und durch die Formel (12) veranschaulicht, die im vorliegenden Falle, wo r = r0 zu setzen ist, also lautet:
| (86) |

|
Liegt diese Achse ζ in der Meridianebene des Punktes M und schliesst sie mit der Aequatorebene den Winkel ξ ein, so ist ζ = ξ - φ, d. h.
| (87) |

|
Liege die Achse ξ nicht in der Meridianebene des Punktes M, so wäre die obige Formel durch eine andere zu ersetzen, die aber nicht aufgeschrieben werden muss, weil von derselben nachstehend kein Gebrauch zu machen sein wird.
Jeder durch den Erdmittelpunkt gehenden Achse ξ entspricht ein eindeutig gegebener Wert des Skalars dΩ, also dem Durchstosspunkt E der Achse ξ mit der Erdoberfläche ein bestimmter Wert dΩ, wodurch die Erdoberfläche zu einem sphärischen Feld des Skalars dΩ wird. Fragen wir, was ist der Gradient dieses Feldes an jener Stelle der Erdoberfläche, die durch die Lage des in Betracht gezogenen Poles, sagen wir des Nordpoles P, gekennzeichnet ist. Dieser Gradient muss aus Symmetriegründen in die Meridianebene des Puntes M fallen, d. h. den Meridian kreis des Punktes M im Punkte P tangieren. Er ist nach der Seite des zunehmenden Skalars dn, d. h. des zunehmenden dΩ gerichtet und hat einen skalaren Betrag, der durch

|
gegeben ist. Dieser Gradient ist, weil er nach den gemachten Vereinbarungen über das Koordinatensystem X-Y-Z dem Einheitsvektor 𝖏 entgegengesetzt gerichtet ist, durch den Ausdruck veranschaulicht:
| (88) |

|
Multipliziert man diese Gleichung vektoriell mit dem Einheitsvektor 𝖐, so wird, weil [𝖐𝖏] =/nbsp;-[𝖏𝖐] = -𝖎 ist,
| (89) |

|
Es folgt aus (85) und (89)
| (90) |

|
Dies ist das von der auf die Masse dμ wirkenden Horizontalkraft herrührende Drehmoment in bezug auf den Erdmittelpunkt. Das von den auf die gesamte isostasische Decke wirkenden Horizontalkräften herrührende Drehmoment wird durch die über die ganze Erdoberfläche sich erstreckende Integration des obigen Ausdruckes erhalten und ist, weil gp, ga, 𝖐 konstante Grössen sind, durch den Ausdruck veranschaulicht:
| (91) |

|
Weil ganz allgemein

|
ist, erhält man:
| (92) |

|
Dieses Drehmoment wird das Bestreben haben, die isostasische Decke der Erde über ihre fluidale Unterlage um eine Achse zu drehen, die wegen des Faktors 𝖐 im obigen vektoriellen Klammerausdruck in der Ebene des Aequators liegt. Die durch dieses Drehmoment bewirkte Verlagerung der Decke kann nur sehr langsam und mit Ueberwindung von Hindernissen erfolgen, weshalb die Rotationsgeschwindigkeit 𝖜 dieser Drehbewegung dem Drehmoment 𝕸 proportional sein wird. Es folgt daraus:
| (93) |

|
worin m ein Proportionalitätsfaktor ist.
Infolge dieser Drehbewegung wird jeder Punkt der isostasischen Decke der Erde mit einer Geschwindigkeit [𝖜𝖗] über die Unterlage gleiten, wobei den Ortsvektor des in Betracht gezogenen Punktes der Decke in bezug auf den Erdmittelpunkt bedeutet. Für den am Drehpol P liegenden Punkt dieser Decke ist 𝖗 = r0𝖐 zu setzen, so dass dessen Verlagerunsgeschwindigkeit in bezug auf das Koordinatensystem X-Y-Z gIeich r0[𝖜𝖐] ist. Der Drehpol P der Erde wird sich mit entgegengesetzter Geschwindigkeit relativ zur Erdkruste bewegen, weshalb seine Geschwindigkeit, d. h. die Geschwindigkeit der Polwanderung durch den Ausdruck:
| (94) |

|
dargestellt ist.
Es folgt aus (94) und (93)
| (95) |

|
Wendet man die bekannte Formel

|
der Vektorrechnung an, so ist, weil der Gradient von Ω im Punkte P senkrecht auf dem Vektor 𝖐 steht, also (𝖐 grad Ω) = 0 ist,
| (96) |

|
Setzt man
| (97) |

|
wobei n wieder einen konstanten Koeffizienten bedeutet, so wird:
| (98) |

|
Diese Gleichung besagt, wie die Gleichung (45), dass der Geschwindigkeitsvektor der säkularen Polbewegung proportional dem Gradient des Feldes Ω und die säkulare Polbahnkurve eine Vektorlinie des Feldes grad Ω ist.
Die Uebereinstimmung dieser gleichlautenden Aussagen der Gleichungen (45) und (98) bliebe aufrecht, selbst wenn infolge der verschiedenen vereinfachenden Annahmen, die bei der Ableitung dieser beiden Gleichungen gemacht worden sind, die numerischen Werte der durch (44) bzw. (97) gegebenen Koeffizienten n untereinander nicht ganz gleich wären, denn diese Werte haben keinen Einfluss auf die Bahnkurve des Poles. Diese hängt nur von der Konfiguration der isostasischen Decke der Erde, d. h. von jener des Feldes Ω ab, über dessen Geometrie einiges berichtet werden möge.
§ 61. Allgemeine Eigenschaften des Feldes Ω und der Polbahnkurven.
§ 62. Die Gleichung der ungestörten Polbahnkurve.
§ 63. Die säkulare Bewegung des Poles längs seiner Bahnkurve.
Kapitel XII
Numerische Ausrechnung und kartographische Veranschaulichung der säkularen Polwanderungen
§ 64. Grundlagen der Berechnung.
§ 65. Gang und Ergebnis der Berechnung.
§ 66. Vergleich des durch die vorstehende Berechnung erhaltenen Ergebnisses mit den Dokumenten der Erdgeschichte. Die durch die vorstehende Berechnung erhaltene säkulare Bahnkurve des nördlichen Drehpoles der Erde ist in der Fig. 32 kartographisch dargestellt. Aus dieser Figur ist zu ersehen, dass sich dieser Pol vor unendlich langen Zeiträumen weit im Pazifischen Ozean, an der geographischen Breite von rund 2G° nördlich und an der geographischen Länge von rund 168° westlich befunden hat. Es ist dies eine labile Lage des Gleichgewichts, die der Pol bei der geringsten Störung, und solcher gab es während der Vorzeit viele hat verlassen müssen. Trotzdem hat es sehr langer Zeiten gebraucht, bis sich der Pol aus dieser Lage hat entfernen können, denn in der Umgebung dieser Stellung ist der Gradient des Trägheitsmomentfeldes Ω und dadurch auch die Geschwindigkeit der Polverlagerung ausserordentlich klein. Erst als sich der Pol um 1° bis 2° aus jener labilen Lage des Gleichgewichts entfernt hatte, erhielt seine Blewegung einen fühlbaren Schwung. Der Pol bewegte sich, seine Anfangslage verlassend, zuerst in östlicher Richtung, um dann, allmählich nach links umbiegend den Weg gegen Norden einzuschlagen. Dabei wurde die Geschwindigkeit seiner Bewegung immer grösser, um an der geographischen Breite von 64° ihr Maximum zu erreichen. Die Geschwindigkeit der Bewegung nahm dann fast unmerklich ab, so dass der Pol mit nur wenig verminderter Geschwindigkeit die Nordwestecke des amerikanischen Kontinents überquerte und mit weiter abnehmender Geschwindigkeit seine gegenwärtige Lage erreichte. Von da ab wird er sich mit ständig abnehmender Geschwindigkeit dem an der geographischen Breite von 65° 16′ nördlich und an der geographischen Länge von 49° 34′ östlich (unweit der Petschoramündung) liegenden Endpunkt seiner Bahn asymptotisch nähern, um ihn nach unendlich langer Zeit zu erreichen. Die Bewegung des südlichen Drehpoles der Erde erfolgte antipodisch der soeben beschriebenen.

Die aus dem im Kapitel XI beschriebenen Mechanismus sich ergebende Bewegung der Drehpole der Erde ist also eine aperiodische, d, h. eine ihrem Wesen nach grundverschiedene von jener, wie sie von Reibisch, Kreichgauer, Simroth und dem bereits erwähnten Loeffelholz von Colberg angenommen und gelehrt wurde. Nach dem hier entwickelten Mechanismus hat jeder der beiden Drehpole der Erde eine nicht umkehrbare Bewegung vollführt, wobei die durch diese Bewegung erzielbare maximale Entfernung zwischen der Anfangslage und der Endlage 90° Breitegrade beträgt.
Auch zahlreiche geologische Zeugnisse sprechen unzweideutig dafür, dass sich die Lage der Klimazonen der Erde, also auch jene der beiden Pole, im Laufe der Vorzeit sehr beträchtlich geädert haben musste. Mit Benützung dieser Zeugnisse war es möglich, die Verlagerungen des Erdäquators und der zugehörigen Pole mit einiger Sicherheit durch die Vorzeit zu verfolgen. W. Köppen hat diese auf empirischem Wege gewonnene Polbahnen besprochen und mit der von mir berechneten Polbahn verglichen (Meteorologische Zeitschrift 1940). Ich will diesen Vergleich mit der von Kreichgauer entworfenen Polbahn durchführen, die sich ohne Berücksichtigung der Kontinentalverschiebungen ergeben hat, was den hier gemachten Voraussetzungen vollkommen entspricht Zu diesem Zwecke benutze ich eine von Kreichgauer herrührende Erdkarte, die Wegener in seinem Werke veröffentlicht hat und die mit einer sogleich zu besprechenden Ergänzung in der beiliegenden Fig. 33 wiedergegeben ist. Man erblickt darin die Lagen der beiden Pole zur Zeit des Silurs, des Karbons und des Tertiärs samt, den zugehörigen Aequatorkreisen. Ein dicker vermutlich von Wegener eingezeichneter Strich, der vom Karbon-Nordpol längs des Meridiankreises von 150° westlicher Länge gegen Norden führt, gibt die beiläufige mittlere Bahn des Nordpoles an. Diese Figur ist durch die Eintragung der hier berechneten Bahnkurve des nördlichen Drehpoles der Erde ergänzt worden. Dies geschah in der Weise, dass neun Punkte dieser Kurve, durch kleine Kreise umringelt und durch die der Fig. 32 entnommene Numerierung versehen, an den aus der Berechnung sich ergebenden Stellen eingezeichnet wurden. Der dadurch ermöglichte Vergleich der beiden Polbahnkurven, der empirisch bzw. der rechnerisch gefundenen, ist geradezu verblüffend: beide Kurven überdecken sich vom 40. Breitegrad an fast voilständig.

§ 67. Der zeitliche Verlauf der Polverlagerungen. Alle Forscher, die sich bemüht hatten, die Klimazonen des Karbon-Zeitalters auf Grund der geologischen Dokumente zu rekonstruieren, sind darin einig; dass in jenem Zeitalter der Nordpol der Erde im Pazifischen Ozean lag. Kreichgauer gibt, wie aus der Fig. 33 ersichtlich, die Lage an, die durch die geographische Breite vcn 35° nördlich und die geographische Länge von 147° gekennzeichnet ist; Köppen und Wegener weisen diesem Pole eine geographische Breite von 30° und eine geographische Länge von 150° zu. In beiden Fällen lag der Nordpol in der unmittelbaren Nähe der aus der Berechnung sich ergebenden Polbahnkurve. Im ersten Fa1le lag er bei dem mit -8 gekennzeichneten Punkt der Bahnkurve, im zweiten bei dem Punkt, der mit -10 bezeichnet ist.
Die auf Grund radioaktiver Substanzen durchgeführte absolute Zeitmessung hat mit ziemlicher Sicherheit ergeben, dass seit der Mitte des Karbonzeitalters rund 300 Millionen Jahre verflossen sind. Nimmt man also an, der Karbon-Pol sei bei dem mit -10 bezeichneten Punkt der Polbahnkurve zu suchen, so besagt dies, dass 10 Zeiteinheiten, die meiner Berechnung zugrunde gelegt werden, einer Zeitspanne von 300 Millionen Jahren entsprechen. Einer solchen Zeiteinheit entspricht also eine absolute Länge von 30 Millionen Jahren. Man hätte also die in der ersten Kolumne der auf der Seite 275 befindlichen Tabelle enthaltenen Zahlen mit 30 zu multiplizieren, um den zeillichen Verlauf der Polwanderungen in Jahrmillionen auszudrücken.
Nimmt am dagegen an, dem Karbon-Pol entspreche der Punkt -8 der Polbahnkurve, so gelangt man zu einer absoluten Länge der obigen Zeiteinheit von 37,5 Jahrmillionen.
Die beiden obigen absoluten Werte der Zeiteinheit stellen wohl nur ihre obere Grenze dar. Die empirische Lagebestimmung des Karbon-Poles ist nicht derart zuverlässig, um diese Lage auf Grade genau angeben zu können; sie ist einem unvermeidlichen Fehler von mindestens ±5° behaftet. Auch die durch die Berechnung sich ergebende Lage der einzelnen Punkte der Polbahn kann nicht als absolut zuverlässig betrachtet werden, weil wir über die Konfiguration der Erdkruste nur unvollkommen unterrichtet sind. Aus diesem Grunde muss damit gerechnet werden, dass die Berechneten Koordinaten der Trägheitspole dieser Kruste ebenfalls mit einem Fehler von ±5°behaftet sind. Deshalb ist es wohl möglich, dass die tatsächliche Lage des Karbon-Poles in unmittelbarer Nähe des Trägheitspoles, also des mit -∞ gekennzeichneten Punktes der Polbahn gelegen war. In einem solchen Falle wäre die Ermittlung der absoluten Länge der benützten Zeiteinheit nicht gut möglich, denn in der Umgebung dieser Lage liegen die Punkte der Polbahn, die den einzelnen Vielfachen der Zeiteinheit entsprechen, so nahe aneinander, dass die erzielbare Genauigkeit bei der Bestimmune der Lage des Drehpoles bzw. jener des Trägheitspoles viel zu gering ist, um entscheiden zu können, bei welchem Punkte der Bahnkurve der Pol sich wirklich befunden hatte. In diesem kritischen Falle steht uns ein anderer Weg offen, um den unteren Grenzwert der absoluten Länge unserer Zeiteinheit festzulegen.
Die Beobachtungen des Internationalen Breitendienstes ergeben eine säkulare Polwanderung von etwa 1° 20′ pro Jahrmillion. Die beiden mit -1 bzw. mit +l bezeichneten Punkte der in der Fig. 32 veranschaulichten Polbahnkurve liegen wie aus der Tabelle, Seite 275, ersichtlich, 11° 52′ voneinander entfernt. Die Zurücklegung dieser Strecke mit der soeben angegebenen Geschwindigkeit der Polwanderung würde rund 9 Jahrmillionen erfordern. Weil dieser Zurücklegung zwei der Berechnung zugrunde gelegte Zeiteinheiten entsprechen, so würde die absolute Länge einer solchen Zeiteinheit 4,5 Jahrmillionen betragen.
Es folgt aus dem oben gesagten, dass mit Benützung der bisherigen empirischen Ermittlungen der Lage des Poles während der Vorzeit und der auf Grund radioaktiver Substanzen durchgeführten zugehörigen Zeitbestimmung die absolute Länge der oben benutzten Zeiteinheit nur ihrer Grösssenordnung nach festlegen kann. Sie dürfte zwischen 5 und 30 Jahrmillionen liegen. Damit gewinnt man immerhin einen Einblick in den zeitlichen Verlauf der Polverlagerungen.
Diese Verlagerung verlief auf alle Fälle äusserst langsam, so dass sie sich während des Zeitintervalles der letztverflossenen 600 Jahrtausende nicht fühlbar gemacht hatte, weshalb man sie bei der Berechnungen des säkularen Ganges der Erdbestrahiung nicht zu berücksichtigen braucht. Die Verlagerungen der Erdpole hatten keinen Einfiuss auf den Verlauf des quartären Eiszeitalters.
§ 68. Der Einfluss der Polverlagerungen auf die Orientierung der Erdachse im Weltraume. Jede Verlagerung der Drehachse im Erdkörper ist mit einer Aenderung der Orientientierung dieser Achse im Weltraume verknüpft, wie dies im zweiten Abschnitt dieses Buches ausführlich begründet erscheint. Beide Bewegungen hängen, wie im § 30 gezeigt, derart zusammen, dass die Drehachse der Erde im Erdkörper selbst den Polhodiekegei, im Raume aber den Herpolhodiekegel beschreibt, so dass die Drehbewegung der Erde derart vor sich geht, wie wenn der mit der Erde fest verbundene Polhodiekegei auf dem Herpolhodiekegel ohne zu gleiten rollen würde.
Die vorstehend ermittelte und durch die Fig. 32 veranschaulichte säkulare Bahnkurve des nördlichen Drehpoles der Erde stellt den Schnitt des Polhodiekegel mit der Erdoberfläche dar. Dadurch ist dieser Kegel selbst eindeutig gegeben. Die Erdachse verlagert sich auf diesem Kegel mit einer Geschwindigkeit, deren Grenzen soeben festgesteilt werden konnten. Dabei vollführt die Erde während eines Sterntages eine volle Drehung in bezug auf den Fixsternhimmel. Dies alles ermöglicht, auch jene Grenzen zu ermitteln innerhalb deren der Herpolhodiekegel eingeschlossen erscheint.
Die obere Grenze der Oeffnung des Herpolhodiekegeis wird erhalten, wenn man der Polverlagerung die obere Grenze ihrer Geschwindigkeit zuweist. Mit seiner gegenwärtig möglichen maximalen Geschwindigkeit verlagert sich der Drehpol um 5° 56′ pro Zeitintervall von 4,5 Jahrmillionen. Als der Drehpol einst an der geographischen Breite vou 64° seine grösste Verlagerungsgeschwindigkeit erreicht hatte, hat er sich, wie aus der Tabelle, Seite 275 ersichliich, während des obigen Zeitintervalles von 4,5 Jahrmillionen um 8° verlagert. Die Geschwindigkeit seiner Verlagerung betrug also damals 0″ 0000175 pro Sterntag. Auf der Erdoberfläche ist arc 1″ = 30,85m, so dass die schnellste Verlagerung des Drehpoles auf der Erdoberfläche 0,73 Millimeter pro Sterntag betrug. Diese sehr kleine Länge stellt als Folge des erwähnten Abrollens des Polhodiekegeis auf dem Herpolhodiekegel den Umfang des Schnittes des Herpolhodiekegeis mit der Erdoberfläche dar. Dies beweist, dass dieser Kegel ausserordentiich spitz ist und deshalb die räumliche Orientierung der Drehachse der Erde in bezug auf den Fixsternhimmel durch die säkularen Polverlagerungen fast gar nicht geändert wird. Diese Orientierung wird nur durch die im zweiten Abschnitt dieses Buches ausführlich behandelte Präzession und Nutation der Erdachse auf die dort beschriebene Weise geändert, was bei der Berechnung der säkularen Aenderungen der Erdbestrahlung berücksichtigt werden muss.
Für einen ausserhaib der Erde befindlichen Beschauer verlaufen die Verlagerungen der Pole in der Weise, dass ihre Verbindungslinie, d.h die Erdachse im Raume ihre Orientation behält, aber die Erdkruste über ihrer Unterlage sich derart verschiebt, dass der Nordpol der Erde die durch die Fig. 32 dargestellte Kurve auf der Erdoberfläche verzeichnet.
§ 69. Nebeneinflüsse. Die hier berechnete und in der Fig. 32 eingezeichnete Kurve stellt die ungestörte Bahn des nördlichen Drehpoles in bezug auf die Erdoberfläche dar. Die Bahn des Südpoles liegt antipodisch gelagert zu jener des Nordpoles. Beide Kurve haben während der Vorzeit mancherlei Veränderungen erfahren, denn jede Aenderung des vorstehend als permanent Vorausgesetzen Trägheitsmomentfeldes Ω der Erdkruste beeinflusst, wie dies schon aus der Grundgleichung (45) der Polverlagerungen unmittelbar folgt, die Bewegung der Drehpole. Damit sich aber diese Einflüsse fühlbar machen, müssen die Veränderungen des Trägheitsmomentfeldes einen entsprechenden Schwellenwert erreichen. Es ist Aufgabe geophysikalischer Forschung, festzustellen, wie und wann solche Veränderungen des Antlitzes der Erde stattgefunden haben. Dann wird es mit Hilfe der Grundgleichung (45), in der Ω nicht mehr als konstant zu betrachtet ist, möglich sein, die Störungen der Polbahnkurven zu ermitteln. Eine dieser Störungen kann schon jetzt besprochen werden. Sie fand während der quartären Eiszeit statt. Die damals über einen grossen Teil von Europa und Nordamerika lagernde mächtige Eisdecke hat, wie dies rechnerisch ermittelt werden kann, den Trägheitspol der Erde längs des Meridianes von 105° 2&prime, östlich, also in der Richtung gegen das Kap Tscheljuskin um 9′ verlagert. Dies wäre also die Richtung und das Ausmass der Anomalie des Trägheitspoles, die, wie dies aus der Gleichung (43) folgt, dem Geschwindigkeitsvektor 𝖛 der durch diese Anomalie hervorgerufenen Polverlagerung proportional ist. Die durch die Eisbedeckungen hervorgerufene Störung des Feldes Ω hatte also das Bestreben, die säkulare Bewegung des Nordpoles in der angegebenen Richtung, also gegen Osten abzulenken. Dieses Bestreben dauerte nicht lange, denn die von Eis bedeckten Teile der Kontinentalschollen tauchten, dem Isostasieprinzip gehorchend, allmählich tiefer in ihre fluidale Unterlage ein, wodurch sich jene Anomalie und dadurch auch der Geschwindigkeitsvektor der Polbewegung verminderten. Als aber nachher, mit dem Eintritt warmer Zeiten, die Eisdecke weggeräumt wurde, die entlasteten Kontinentalschollen aber noch nicht zu ihrer ursprünglichen Tauchtiefe emporgestiegen waren, änderte die Anomalie des Trägheitspoles und damit auch die störende Kraft ihr Vorzeichen, so dass sie in der Richtung des Meridianes von 75° westlich wirksam wurde. Dies ist, weil das Emportauchen der einst belasteten Kontinentalschollen noch nicht ganz beendet ist, auch gegenwärtig der Fall, so dass der Pol noch immer gegen Westen abgelenkt wird. Er kehrt dadurch zu seiner ursprünglichen Bahnkurve zurück, um bis zu der nächsten Störung in ihr zu verbleiben.
Vierter Abschnitt
Die Bestrahlung der Erde durch die Sonne und die säkularen Aenderungen dieser Bestrahlung
Kapitel XIII
Der gegenwärtige Bestrahlungszustand der Erde
§ 70. Die Solarkonstante. Die Sonne ist eine unerschöpflich scheinende Quelle der strahlenden Energie, die sich aus diesem Born mit Lichtgeschwindigkeit in den weiten Weltraum fortpflanzt. Um die Ergiebigkeit dieser Quelle zu definieren und mathematisch zum Ausdruck zu bringen, denke man sich um die Sonne eine ihr konzentrische Kugelfläche gelegt, deren Radius r genügend gross sein möge, um annehmen zu können, dass die von der Sonne ausströmende Strahlung radial durch die Flächenelemente dieser Kugel hindurchfliesse. Man verlängere die Rotationsachse der Sonne bis zu ihren Durchstosspunkten mit jener Kugelfläche, verbreite desgleichen die Aequatorebene der Sonne bis zum Schnitte mit jener Fläche. Auf diese Weise hat man auf jener gedachten Kugelfläche einen Aequatorkreis und die zugehörigen Pole festgelegt und ist in der Lage, jeden ihren Punkt durch zwei Koordinaten φ und ψ zu kennzeichnen, wobei φ die heliographische Breite und ψ die heliographische Länge, gezählt von einem hiezu gewählten Meridian, bedeuten möge.
Man grenze nun an einer beliebigen Stelle jener Kugel die Flächeneinheit ab, bezeichne mit dQ jene Energiemenge der Sonnenstrahlung, die während des Zeitelementes dt durch diese Flächeneinheit hindurchströmt, dann ergibt es sich, dass durch diese Flächeneinheit während der Zeiteinheit eine Energiemenge:
| (1) |

|
durchfliesst.
Diese Grösse wird der Energiefluss oder die Intensität der Sonnenstrahlung an der in Betracht gezogenen Stelle genannt.
Es wäre vielleicht zu erwarten, dass die Grösse J nicht nur eine Funktion von r, sondern auch eine solche der Kooidinaten φ und ψ und der Zeit t sein werde, weist doch die Oberfläche der Sonne örtliche, zeitlich veränderliche Ungleichmässigkeiten auf, die die Ausstrahlung der Sonne beeinflussen dürften. Die bisherigen Beobachtungen, die sich, weil die Ebene der Erdbahn einen Winkel von 7° 10′ mit der Ebene des Sonnenäquators einschliesst, auf das Intervall -7° 10′ < φ < +7° 10′ erstreckten, haben indessen eine Abhängigkeit der Grösse J von der heliographischen Breite nicht ergeben; auch die Veränderlichkeit dieser Grösse mit der heliographischen Länge ψ und der Zeit t schwankt um einen MittelweIt zwischen engen Grenzen. Eliminiert man diese Schwankungen durch die Ermittlung eines auf ein längeres Zeitintervall sich erstreckenden Mittelwertes, so kann die Intensität der Sonnenstrahlung auf der ganzen angegebenen Kugelfläche als räumlich und zeitlich unveränderlich betrachtet werden.
Man denke sich nun eine andere mit der Sonne konzentrische Kugelfläche mit dem Radius a, wobei a die mittlere Entfernung der Erde von der Sonne der die grosse Halbachse der Erdbahn. bedeutet, so wird der nach dem obigen gleichmässige Energiefluss durch die Flächenelemente dieser Kugel die Solarkonstante genannt. Ich werde diese Grösse stets mit J0 bezeichnen. Man drückt diese Grösse gewöhnlich in Wärmeeinheiten aus, so dass man sie wie folgt definieren kann: Die Solarkonstante ist jene, vollkommen in Wärme umgewandelt gedachte strahlende Energie der Sonne, die während der Zeiteinheit durch die in der mittleren Entfernung der Erde von der Sonne senkrecht zur Strahlungsrichtung orientierte Flächeneinheit ungehindert durchströmt, wobei die periodischen Schwankungen der Sonnenstrahlung zu eliminieren sind. Dabei wird als Zeiteinheit die Minute, als Flächeneinkeit der Quadratzentimeter und als Wärmeinheit die Grammkalorie gewählt.
Es hat lange gedauert, bis es der beobachtenden Forschung gelungen ist, den numerischen Wert der Solarkonstante mit befriedigender Genauigkeit zu ermitteln; er beträgt nach den neuesten Beobachtungen 1.946 Grammkalorien pro cm2 und Minute, doch ist dieser Wert noch nicht als ein endgültiger zu betrachten. Ich werde deshalb bei meinen Berechnungen des säkularen Ganges der Erdbestrahiung die Solarkonstante zur Wärmeeinheit wählen, um die numerischen Daten dieser Berechnung von der obigen Zahl unabhängig zu machen.
§ 71. Das Bestrahlungsgesetz. Die Abhängigkeit der Intensität der Sonnenstrahlung von dem heliozentrischen Abstand r ergibt sich aus dem vorstehenden wie folgt. Durch die im vorigen Paragraphen angegebene Kugelfläche vom Radius r fliesst während der Zeiteinheit die Strahlungsmenge 4 · π · r2 · J hindurch, durch die Kugelfläche vom Radius a die Strahlungsmenge 4 · π · a2 · J. Beide Mengen sind, unter der Voraussetzung, dass in dem Zwischenräume der beiden Kugeln keine Absorption der Strahlung stattfindet, einander gleich, so dass man bekommt:
| (2) |

|
oder wegen (1)
| (3) |

|
Wird, wie dies in Hinkunft geschehen soll, die Entfernung r mit dem Erdbahnhalbmesser a gemessen und das Ergebnis dieser Messung mit ρ bezeichnet, d. h. wird
| (4) |

|
gesetzt, so erhält man statt (3)
| (5) |

|
Bisher wurde angenommen, dass die Sonnenstrahlung auf die in Betracht gezogene Flächeneinheit senkrecht auffällt. Ist dies nicht der Fall, sondern schliesst die Normale BN (Fig. 34) der bestrahlten, gegen die Strahlungsrichtung schief gestellten Flächeneinheit AB mit dieser Richtung den Incidenzwinkel z ein, so wird diese Fläche während der Zeiteinheit nicht der durch (2) gegebenen Strahlung teilhaftig, sondern jener, die durch das Strahlenbündel mit der Basis AE zugeführt erscheint.

Weil diese Basis gleich AB · cos ∠BAE = cos z ist, wird dem Flächenelement AB während der Zeiteinheit die Strahlungsmenge
| (6) |

|
oder wegen (2) und (4) die Strahlungsmenge
| (7) |

|
zugeführt.
Diese Grösse wird die Bestrahlung oder die Insolation des in Betracht gezogenen Flächenelements genannt.
Benützt man die vostehenden Gleichung zur mathematischen Beschreibung der Bestrahlung der Erde durch die Sonne, setzt die Erdoberfläche als vollkommen eingeebnet voraus, so dass sie aus lauter horizontalen Flächenelementen zusammengesetzt erscheint und zieht ein solches die Flächeneinheit messendes Element der Erdoberfläche in Betracht, so ist der Incidenzwinkel z der auf dieses Element auffallenden Sonnenstrahlen gleich der dem Orte dieses Elementes zukommenden augenblicklichen Zenitdistanz der Sonne, welche Distanz in Hinkunft ebenfalls mit z bezeichnet werden möge. Der Abstand des in Betracht gezogenen Flächenelementes von der Sonne ist, weil die Abmessungen der Erde verschwindend klein sind im Vergleich zur Entfernung der Erde von der Sonne, gleich dieser Entfernung, besser gesagt der Entfernung des Erdmittelpunktes vom Sonnenmittelpunkte. Ich werde diese Grösse, die dem Radiusvektor der Erdbahn gleich ist und die ich mit der mittleren Entfernung a der Erde von der Sonne messen will, ebenfalls mit ρ bezeichnen.
Zieht man also die an der geographischen Breite φ befindliche horizontale Flächeneinheit der Erdoberfläche in Betracht, so ist die Insolation derselben in einem gegebenen Augenblicke, dem die Zenitdistanz z und die Entfernung ρ der Sonne entspricht, durch die Formel (7) veranschaulicht. Bezeichnet ω den in Bogenmass gemessenen Stundenwinkel und δ die Deklination der Sonne, so besteht nach der Formel (200) des zweiten Abschnittes dieses Buches zwischen den Grössen z, φ, δ und ω die Gleichung:
| (8) |

|
Setzt man dies in (7) ein so bekommt man:
| (9) |

|
Diese Formel drückt das Gesetz der Bestrahlung der Erde durch die Sonne aus.
Bei der Anwendung dieser Formel muss folgendes berücksichtigt werden. Sobald die Zenitdistanz z der Sonne den Wert von 90° erreicht, wird nach (8) die rechte Seite der Gleichung (9) gleich Null; die Sonne ist unter den Horizont des in Betracht gezogenen Ortes der Erde gesunken und dieser Crt bleibt unbestrahlt bis zum nächsten Sonnenaufgang. Man muss von dieser Diskontinuität der Bestrahlung eines in Betracht gezogenen Elementes der Erdoberfläche Rechnung tragen und darf die Integration der Gleichung (9) nicht auf ein beliebiges Zeitintervall t0 bis t1 erstrecken, also nicht etwa schreiben:

|
bevor man die Grenzen t0 und t1 derart ermittelt hat, dass sie dem Tagesintervall des in Betracht gezogenen Ortes angehören, oder dieses Tagesintervall begrenzen. Die Grenzen dieses Tagesintervalles hängen, wie man sehen wird, auch von der geographischen Breite φ des Ortes ab und sind von Breite zu Breite verschieden. Man darf deshalb nicht etwa wie folgt schliessen: Setzt man in der obigen Gleichung φ = 0, so bekommt man die am Aequator zugestrahlte Wärmemenge Wa; setzt man φ = +90°, so erhält man die dem einen oder dem anderen Pole Zugestrahlte Wärmemenge Wp also
| (10) |

|
Diese Gleichung kann nie stimmen, weil an der geographischen Breite φ den Grenzen t0 und t1 ganz andere numerische Werte entsprechen als am Aequator bzw, an den Polen. Von diesem Umstand hat man in der Literatur nicht immer Rechnung getragen und hat mitunter die obige unrichtige Formel zur Grundlage der Berechnung der Erdbestrahlung gemacht, wodurch man natürlich zu ganz falschen Schlüssen gekommen ist, wie ich dies in meiner "Theorie mathématique" berichtet habe. In meiner "Mathematischen Klimalehrer" und in meinen "Astronomischen Mitteln", wo ich ebenfalls über die einschlägige Literatur berichtete, habe ich jene Arbeiten, die auf der obigen falschen Formel beruhen, nicht mehr berücksichtigt und sie in das Literaturverzeichnis nicht eingeordnet, weil sie, als falsch, keinen Bestandteil der Wissenschaft bilden.
Zur Berechnung der Erdbestrahlung muss der bereits in einigen klassischen Abhandlungen von Meech, Wiener und Hargreaves betretene Weg eingeschlagen werden, der, von mir gründlicher ausgebaut, nachstehend beschrieben werden möge.
§ 72. Die Bestrahlung der Erde in einem gegebenen Zeitpunkte.
§ 73. Der tägliche Bestrahlungsgang.
§ 74. Die täglichen Strahlungsmengen.
§ 75. Die Diskontinuität des Bestrahlungsganges und deren Elimination.
§ 76. Reihenentwicklungen.
§ 77. Der jährliche Gang der Bestrahlung.
§ 78. Die während beliebiger Zeitabschnitte des Jahres zugestrahlten Wärmemengen.
§ 79. Die astronomischen Jahreszeiten.
§ 80. Quantitäten der Bestrahlung während der astronomischen Jahreszeiten.
§ 81. Die den beiden Hemisphären während beliebiger Intervalle des Jahres zugestrahlten Wärmemengen.
Kapitel XIV
Säkulare Änderungen der den Bestrahlungszustand der Erde bestimmenden astronomischen Elemente
§ 82. Mechanismus der säkularen Aenderungen der den Bestrahlungszustand der Erde bestimmenden astronomischen Elemente. Es stelle in der beiliegenden Fig. 40 der Punkt S den Mittelpunkt der Sonne und die Ellipse PIAIIIP die jährliche Bahn der Erde um die Sonne dar.

Denkt man sich in S eine gegen die Nordseite der Himmelskugel gerichtete Senkrechte SV zur Ebene der Erdbahn errichtet und die Parallele SN zur Rotationsachse der Erde gezogen, dann stellt der Winkel VSN die Neigung der Rotationsachse der Erde oder die Schiefe ε der Ekliptik dar. Die durch die Geraden SV und SN gelegt gedachte Ebene E steht senkrecht auf der Ebene der Erdbahn und schneidet diese längs der Geraden II IV. Die Punkte II und IV stellen, wie leicht einzusehen, die Solstitiallagen der Erde in ihrer Bahn dar, und wenn in der Ebene der Erdbahn durch S eine Senkrechte zur Geraden II IV gezogen wird, so trifft diese die Erdbahn in den Punkten I und III, welche die beiden Aequinoktiallagen der Erde veranschaulichen. Die Zeitintervalle, welche zwischen den Durchgängen der Erde durch die vier Kardinalpunkte I, II, III, IV verfliessen, stellen die astronomischen Jahreszeiten dar; dabei entspricht das Bahnintervall I II III dem nördlichen Sommerhalbjahr Ts, das Bahnintervall III IV I dem nördlichen Winterhalbjahr Tw. Die Ungleichheit dtr Sektoren I II III und III IV I hat die Ungleichheit dieser Halbjahre zur Folge. Die Lage dieser vier Punkte der Erdbahn wird durch den Winkel III SP festgelegt, wobei P den der Sonne am nächsten gelegenen Punkt der Erdbahn, das sogenannte Perihel, darstellt. Der Winkel III SP, der mit II, bezeichnet werden möge, wird die Länge des Perihels zum Frühlingspunkt genannt, weil die Sonne zur Zeit des Frühlingsäquinoktiums in der Richtung IS auf der Himmelskugel projiziert erscheint und der Durchstosspunkt der Geraden IS mit der scheinbaren Himmelskugel der Frühlingspunkt genannt wird. Befindet sich dagegen die Erde im Punkte P ihrer Bahn, so befindet sich die Sonne im Perigeum ihrer relativen Bahn zur Erde. Es stellt deshalb der Winkel A S III, den die Richtungen PS und IP mit einander einschliessen, die Anomalie ν0 des Frühlingspunktes dar. Weil die Punkte P und A diametral, d. h. auf einer durch S hindurchgehenden Geraden gelegen sind, so folgt aus der Fig. 40
| (111) |

|
Wenn die Planeten in ihrem Lauf sich nicht gegenseitig stören würden und wenn auch die Rotationsachse der Erde ihre Orientierung im Weltraume beibehielte, würde die in der Fig. 40 veranschaulichte Bahnkurve der Erde unwandelbar und die Kardinalpunkte I, II, III, IV derselben unverrückbar sein. Der im vorhergehenden Kapitel geschilderte jährliche Bestrahlungsgang der Erde würde sich ohne Aenderung Jahr für Jahr wiederholen. Dies ist aber nicht der Fall. Die im Kapitel VI dieses Buches geschilderde Präzession der Drehachse der Erde würde, wenn sie allein wirksam wäre, die zu dieser Drehachse parallel gezogene Gerade SN derart verlagern, dass sie während eines Zeitintervalles von rund 26.000 Jahren den Kreiskegel NSM beschreiben würde. Die Achse dieses Kegels ist SV, sein Oeffnungswinke1 ε. Infolge dieser Drehung der Erdachse dreht sich die Ebene E um die Gerade SV als Achse, und die Kardinalpunkte I, II, III, IV wandern im Sinne des Uhrzeigers längs der Erdbahn. Sie würden auch während des erwähnten Zeitintervalles von 26.000 Jahren einen ganzen Umlauf um diese Bahn vollführen, wenn diese Bahn unveränderlich wäre. Infolge der gegenseitigen Störungen der Planeten eilt aber die grosse Achse der Erdbahnellipse den Kardinalpunkten entgegen, weshalb diese Punkte einen vollständigen Umlauf um diese Bahn (vom Perihel bis Perihel) in rund 22.000 Jahren vollführen. Während dieser Zeit, die nur als ein Durchschnittswert zu betrachten ist, nimmt die Grösse Πγ, um 360° zu.
Durch die gegenseitigen Störungen der Planeten ändert die Erdbahn allmählich ihre Form; ihre grosse Halbachse bleibt dabei, wie im § 19 berichtet, ihrer Grösse nach ungeändert, aber die Exzentrizität e dieser Bahn ist nicht unbedeuten den säkularen Aenderungen unterworfen. Auch die Ebene dieser Bahn schwankt im Raume, weil die astronomischen Elemente Ω und i, die die Lage dieser Ebene im Raume festlegen, säkular veränderlich sind, wodurch auch die Schiefstellung ε der Drehachse SN der Erde zur Erdbahn in Mitleidenschaft gezogen wird. Eine weitere Folge der Schwankungen der Erdbahnebene ist, dass die bisher als unveränderlich angenommene Gerade SV ihre Orientierung im Raume allmählich ändert, wodurch der Kegel NSM seine Unbeweglichkeit und Regelmässigkeit verliert.
Die soeben kurz geschilderten Aenderungen der astronomischen Elemente lassen sich mit Benützung der im ersten und zweiten Abschnitt dieses Buches mitgeteilten Lehren der Himineismechanik mathematisch exakt erfassen und in Vergangenheit und Zukunft während langer Zeitintervalle Schritt für Schritt verfolgen. Aus diesen Aenderungen lassen sich mit Hilfe des Bestrahlungsgesetzes und mit derselben Genauigkeit die daraus resultierenden Veränderungen der Erdbestrahlung, also der von mir so benannte säkulare Bestrahlungsgang der Erde berechnen. Dieser säkulare Bestrahlungsgang, die Ursache der wichtigsten vorzeitlichen Aenderungen des Erdklimas, wird den Gegenstand meiner nachfolgenden Untersuchungen bilden. Dabei wird folgendes zu berücksichtigen sein.
Die Bestrahlung der Erde durch die Sonne hängt nur von der Form der Erdbahn und der Orientierung der Erdachse in bezug auf diese Bahn ab, nicht aber von der Lage dieser Bahn im Weltraume. Diese gegenseitige Lage der Sonne, Erde und ihrer Achse ist durch die astronomischen Elemente Πγ, ε und ν0 eindeutig gegeben, so dass bloss die säkularen Aenderungen dieser drei Elemente von Einfluss auf den Bestrahlungszustand der Erde sind. Dies folgt auch daraus, dass in den im vorstehenden Kapitel abgeleiteten Formeln, mittels denen alle auf die Bestrahlung der Erde durch die Sonne bezughabenden Fragen beantwortet werden können, von den astronomischen Elementen nur die drei: e, ε und ν0 vorkommen, das geozentrische Element ν0 aber mittels der Gleichung (111) durch das heliozentrische Element Πγ ersetzt werden kann.
§ 83. Analytische Darstellung der säkularen Aenderungen der Elemente e, Πγ, ε. Die analytische Darstellung der säkularen Aenderungen der Elemente e, Πγ, ε ist eine Kombination der Formeln der Störungsrechnung und jener der Präzession der Erdachse. Die Grundzüge dieser Analysis sind die folgenden:

In der beiliegenden Fig 41 stelle X-Y-Z das im § 11 gekenzeichnete ruhende Koordinatensystem dar, dessen Ursprung O in der Sonne gelegen ist, dessen X-Y-Ebene mit der zum Ausgangspunkt der Betrachtungen gewählten Epoche t0 zugehörigen Ebene der Erdbahn zusammenfällt und dessen X-Achse gegen den Frühlingspunkt dieser Epoche gerichtet ist. E0, E0′ sei der Schnittkreis der Himmelskugel mit der X-Y-Ebene, d. h. mit der dem Zeitpunkt t0 zugehörigen Ebene der Erdbahn, und Y0 der dem Zeitpunkt t0 zugehörige Frühlingspunkt. Die positive Richtung der X-Achse des hier benützten Koordinatensystems stimmt also mit der Richtung SIII der Fig. 40 überein. Zieht man durch O eine zur Erdachse parallele gegen Norden gerichtete Gerade SN0, so wird diese in der zu O senkrechten Ebene, also in der Y-Z-Ebene des Kordinatensystems liegen und mit der Z-Achse den Winke1 ε0 einschliessen, der der Epoche t0 entsprechenden Schiefe der Ekliptik gleich ist. Die durch O gelegt gedachte Ebene, die der Ebene des Erdäquators parallel ist, also auf ON0 senkrecht steht, wird die Himmelskugel nach dem durch Y0 hindurchgehenden grössten Kreise A0 A0′ schneiden, der mit dem Kreis E0 E0′ ebenfalls den Winke1 ε einschliessen wird. Nach Ablauf eines beliebigen Zeitintervalles, gerechnet vom Zeitpunkt t0 wird die Ebene der Erdbahn, durch die gegenseitigen Störungen der Planeten um den Punkt O gedreht, eine andere Lage als die ursprüngliche einnehmen und die Himmelskugel nach dem grössten Kreise E E′, die X-Y-Ebene nach der Geraden O ☊ schneiden, die, wie bereits im § 11 angegeben, die Knotenlinie genannt wird. Der Bogen Y0 ☊ stellt die Länge Ω des aufsteigenden Knotens, und der Winkel E0′ ☊ E′ die Neigung i der Erdbahn zur Zeit t dar. Auch das Perihel der Erdbahn wird eine andere Lage einnehmen, und während zur Zeit t0 der von der Sonne gegen das Perihel gerichtete Halbstrahl die Himmelskugel im Punkte P0 getroffen hat, wird dies zur Zeit t im Punkte P geschehen. Der Bogen ☊ P stellt die Länge ω des Perihels in bezug auf den aufsteigenden Knoten und die Summe Π = Ω + ω die Länge des Perihels in bezug auf den Punkt Y0, den man auch den fixen Frühlingspunkt nennt, dar. lnfolge der Präzession der Erdachse wird die zu dieser Achse durch O parallele Gerade die Lage ON einnehmen und die durch O zum Erdäquator parallel gedachte Ebene die neue Ebene der Erdbahn nach der zu ON senkrechten Geraden OY schneiden. Der Punkt Y der Himmelskugel veranschaulicht die Lage des Frühlingspunktes zur Zeit t; durch diesen Punkt geht der grösste Kreis AA′ der Himmelskugel, nach dem die Ebene des Erdäquators diese Kugel schneidet. Der Winkel EYA stellt die dem Zeitpunkt t entsprechende Schiefe ε der Ekliptik dar. Macht man den Bogen ☊e gleich dem Bogen ☊Y, so stellt der Bogen eY die sogenannte allgemeine Präzession dar, die mit Ψ′ bezeichnet werden möge. Denkt man sich durch den Punkt Y und die Z-Achse eine Ebene gelegt, so schneidet diese die X-Y-Ebene nach der Geraden OF. Wegen der Kleinheit des Winkels i ist der Bogen Y0F dem Bogen eY gleichzusetzen, so dass der Bogen YF oder der zugehörige Winkel Y0OF ebenfalls die allgemeine Präzession Ψ′ veranschaulicht. Dieser Winkel wird, entgegengesetzt den durch die Fig. 7 getroffenen Vereinbarungen, im Sinne des Umlaufs des Uhrzeigers gezählt, ist also entsprechend dem im § 57 geschilderten Verlauf der Präzession der Nachtgleichen mit dem positiven Vorzeichen zu versehen. Die Summe der Bogen Y0P und Y0F, also die Summe:
| (112) |

|
stellt die Länge des Perihels in bezug auf den jeweiligen oder beweglichen Frühlingspunkt dar. Der Winkel Θ, den die zur Erdachse parallele Gerade ON mit der Z-Achse des ruhenden Koordinatensystems einschliesst, veranschaulicht nach den im § 29 getroffenen Vereinbarungen die zweite Koordinate der Präzession, den Nutationswinkel.
Die analytische Darstellung der säkularen Aenderungen der Elemente e, Πγ, ε geschieht auf folgende Weise.
Mit Benützung der Gleichungen (242) und (279) des ersten Abschnittes dieses Buches, d. h. der Gleichungen:
| (113) |

|
lassen sich bei gegebenen Massen der Hauptplaneten und gegebenen dem Zeitpunkt t = 0 entsprechenden Anfangsbedingungen die säkularen Aenderungen der Exzentrizität e der Erdbahn und der Länge des Perihels Π in bezug auf den fixen Frühligspunkt analytisch darstellen. Diese Aenderungen hängen nur von der gegenseitigen Lage der Planeten und nicht von der Präzession der Erdachse ab.
Auf dieselbe Weise und mittels der Gleichungen (243) und (284) des ersten Abschnittes dieses Buches, d. h. der Gleichungen:
| (114) |

|
worin die numerischen Werte der Grössen Ni, gi, βi verschieden sind von jenen der Ausdrücke (113), erfolgt die analytische Darstellung der säkularen Aenderungen der Neigung i und der Länge Ω des aufsteigenden Knotens der Erdbahn.
Die analytische Darstellung der säkularen Aenderungen der Grössen Ψ′ und Θ erfolgt mit Berücksichtigung der ermittelten säkularen Aenderungen der Erdbahn durch Integration der im § 45 mitgeteilten Bewegungsgleichungen. Dabei ist, weil, wie im § 47 mitgeteilt, der Polhodiekegel der Erdachse einen Oeffnungswinkel von nur 0″0087 aufweist, die Drehachse der Erde mit ihrer Trägheitshauptachse zusammenfallend anzunehmen und nur der permanente, aber wegen der säkularen Aenderungen der Erdbahnelemente säkular veränderliche Bestandteil des Drehmoments in Rechnung zu stellen. Hat man dadurch die Winkel Ψ′ und Θ als Funktionen der Zeit dargestellt, so liefert die Gleichung (112) die säkularen Aenderungen der der Grösse Πγ.
Um die säkularen Aenderungen der Ekliptikschiefe ε analytisch darzustellen, ist zu berücksichtigen, dass dieser Winkel jener ist, den die Drehachse der Erde mit der auf der Ebene der Erdbahn errichteten Normalen einschliesst. Bezeichnet also 𝖓0 den in die Richtung der Erdachse fallenden Einheitsvektor und 𝕮0 den auf der Ebene der Erdbahn senkrecht stehenden Einheitsvektor, so ist:
| (115) |

|
Die Koordinaten n1, n2, n3 und c1, c2, c3 der Vektoren 𝖓0 bzw. 𝕮0 lassen sich wie folgt analytisch darstellen. Trägt man auf die Achse ON die Strecke OL = 1 auf, so ist ihre in die Z-Achse fallende Projektion, also die Koordinate n2, gleich:

|
Die Projektion der Strecke OL in die X-Y-Ebene ist gleich sin Θ; sie steht auf der Geraden OF senkrecht, schliesst also mit der X-Achse den Winkel (90° - Ψ′) ein, weshalb ihre Projektionen in die X-Achse bzw. in die Y-Achse, also die Koordinaten n1 und n2 die folgenden sind:

|
Bezeichnet man also die Einheitsvektoren der Achsenrichtungen X, Y, Z mit 𝖎, 𝖏, 𝖐, so ist:
| (116) |
|
Die Koordinaten c1, c2, c3 des auf der Bahnebene der Erde senkrecht stehenden Einheitsvektors 𝕮0 sind nach den Gleichungen (238) und (244) des ersten Abschnittes dieses Buches gleich:

|
und es ist deshalb:
| (117) |
|
Setzt man (116) und (117) in (115) ein, so bekommt man:
| (118) |
|
§ 84. Numerische Ausrechnungen der säkularen Aenderungen der astronomischen Elemente. Die numerische Ausführung der vorstehend gekennzeichneten Rechnung ist eine riesige Arbeit. Weil sich alle Planeten gegenseitig stören, müssen sie alle in Rechnung gestellt werden, wie dies im § 20 auseinandergesetzt worden ist. Man hat also vor allem aus den gegebenen Massen der Planeten und den grossen Halbachsen ihrer Bahnen mittels der Formeln (250) bis (252) des ersten Abschnittes dieses Buches die in den Differentialgleichungen (277) und (282) auftretenden Koeffizienten (ai, aj), [ai, aj] zu ermitteln, was bei Berücksichtigung von acht Planeten die Berechnung von 80.640 verschiedener numerischer Werte erfordert. Dann sind die Säkulardeterminanten (281) und (286) zu bilden und diese algebraischen Gleichungen achten Grades aufzulösen, um mit ihren Wurzeln und Subdetermimanten und mittels den Anfangsbedingungen die numerischen Werte der in den Integralen (279) und (284) auftretenden Grössen Ni, gi, βi zu berechnen. Um zu diesen Integralen zu gelangen, ist eine Arbeit zu leisten, die Jahre erfordert. Es ist deshalb nicht zu verwundern, dass diese mühselige Arbeit bisher nur einige Male geleistet worden ist.
Der erste, der diese Rechnung durchgeführt hat, war Lagrange. In seiner klassischen Abhandlung "Théorie des variations séculaires des éléments des planetes" (Nouveaux Mémoires de 1′Académie royale des Sciences et Belies-Lettres de Berlin, années 1781 et 1782, abgedruckt in "Oeuvres de Lagrange". Tome V. Paris 1870) hat er im zweiten Teile dieser Arbeit, "contenant la détermination de ces variations pour chacune des planètes principales", die numerische Ausrechnung der säkularen Aenderungen der damals bekannten sechs grossen Planeten durchgeführt. Der Planet Uranus, damals noch der neue Planet genannt, ist während der Abfassung der Abhandlung eben entdeckt worden, seine Elemente waren noch nicht festgelegt, seine Masse war in Unkenntnis seiner erst später entdeckten Satelliten noch unbekannt. Vom Planeten Neptun hatte man damals noch keine Kunde, und Mars galt als satellitlos. Berücksichtigt man, dass, wie im § 10 angegeben, die Masse eines Planeten nur aus der Umlaufszeit seiner Satelliten zuverlässig ermittelt werden kann, so ersieht man, dass Lagrange hinsichtlich der Massenwerte dreier der Erde zunächst liegenden Planeten nur auf rohe Schätzungen angewiesen war. In richtiger Erkenntnis dieses Umstandes hat er auch den Einfluss etwaiger Korrekturen der Massenwerte der Planeten in den Bereich seiner Untersuchungen einbezogen.
Nachdem der erste monumentale Ausbau der Himmelsmechanik durch Lap1ace vollführt war und nachdem Pontécoulant im dritten Bande seiner "Théorie analytique du Système du Monde. Paris 1834." eine mit nur wenig Dezimalen durchgeführte Berechnung der Säkularstörungen der grossen Planeten bewerkstelligt hat, wurde diese Arbeit Ende des vierten Dezeniums des vorigen Jahrhunderts durch Leverrier in vollem Umfang wieder aufgenommen. Die Ergebnisse dieser mehrjĠhrigen Arbeit wurden zuerst im Liouville′schen Journal, Tome V und in der "Connaissance des Temps, 1843" und nachdem Leverrier durch seine auf rechnerischem Wege erfolgte Entdeckung des Planeten Neptun weltberühmt und Leiter des Pariser Observatoriums geworden ist, in den neugegründeten "Annales de l′Observatoire Impérial de Paris. Tome 1, 1855; Tome 11, 1856." veröffentlicht. Im ersten Bande dieser Annalen wurde die Theorie der Planetenbewegung neu durchgearbeitet, im zweiten zur numerischen Berechnung der Säkularstörungen geschritten. Diese in jeder Hinsicht mustergültig angelegten Berechnungen wurden bereits früher, vor der Entdeckung des Neptuns, durchgeführt und weisen nur die eine Unvollkommenheit auf, dass in denselben die störende Wirkung dieses Planeten, die hinsichtlich der Erde allerdings sehr gering ist, nur nachträglich und meritorisch behandelt werden konnte. Dies war wohl die Ursache, dass kurze Zeit nach der Veröffentlichung der Leverrierschen Arbeit Stockwell daran ging, eine Neuberechnung der Säkularstörungen aller damals bekannten acht grossen Planeten durchzuführen. Nach fast zehnjähriger Arbeit wurde diese Berechnung 1870 beendigt und nachher veröffentlicht: J. N. Stockwell, Memoir of the secular variations of the Orbits of the eight principal planets, Mercury, Venus, the Earth, Mars, Jupiter, Saturn, Uranus and Neptune. Smithsonian Contributions to knowiedge. 232. Washington 1873.
Seit dieser Zeit wurde keine brauchbare neue Durchrechnung der Säkularstörungen der grossen Planeten, zu denen unlängst ein neuer, Pluton, hinzugekommen ist, durchgeführt. Wohl unternahm es Harzer, angeregt durch eine Preisaufgabe der fürstlich Jablonowskischen Gesellschaft, in seiner grossen und preisgekrönten Schrift "Die säkularen Veränderungen der Bahnen der grossen Planeten. Leipzig 1895" die in der Ueberschrift dieser Arbeit angegebene Frage zu beantworten, doch wurde, nachdem diese Schrift vollständig gedruckt und ein Teil der Exemplare bereits versandt war, in derselben ein Ansatzfehler entdeckt. Dieser tief bedauerliche im Nachtrag mitgeteilte Umstand entwertete arg die numerischen Ergebnisse der grossangelegten Arbeit.
Von den bisher durchgeführten Berechnungen der säkularen Aenderungen der Erdbahnelemente sind also nur deren zwei für die weitere Verwendung geeignet, jene von Leverrier und jene von Stockwell. Doch sind durch die Arbeiten dieser zwei Astronomen nicht alle erforderlichen Arbeiten geleistet, um zur Berechnung des säkularen Bestrahlungsganges der Erde schreiten zu können. Es blieb noch übrig, die durch die Ermittlung der numerischen Werte der Grössen Ni, gi, βi gewonnenen Integrale (279) und (284) für eine genügende Anzahl der Zeitpunkte des in Betracht zu ziehenden Zeitraumes der geologischen Vorzeit auszuwerten und auch die diesen Zeitpunkten zugehörigen Werte von ε und Πγ zu berechnen.
Ich werde bei meiner Berechnung des säkularen Ganges der Erdbestrahlung deren Ergebnisse in kanonischen Einheiten oder in Metern der Schneegrenzverschiebung ausdrücken. Um selbst für den Anfang des Quartärs und für die höheren geographischen Breiten diese Ergebnisse auf etwa 10 m der Schneegrenzeverschiebung genau zu erhalten, ist es erforderlich die Ekliptikschiefe ε auf 140″, die Exentrizität e der Erdbahn auf 0,001 und die Länge Πγ des Perihels auf 45′ genau zu haben. Die Genauigkeit der Ergebnisse der astronomischen Berechnung der säkularen Aenderungen der Elemente ε, e, Πγ welche diese Angaben zu liefern hat, hängt in erster Linie von der Genauigkeit der numerischen Werte der Planetenmassen, die den Ausgangspunkt dieser Berechnung bilden. Obwohl seit der Zeit der Leverrierschen Berechnung sich unsere Kenntnisse über diese Massenwerte nicht unwesentlich vervollständigt haben, bleibt noch die Frage offen, wie die noch ausstehenden Korrekturen dieser Werte die Ergebnisse der astronomischen Berechnung und meiner darauf fussenden beeinflussen könnten. Eine analytische Behandlung dieser Frage stösst auf unüberwindliche Schwierigkeiten, weil der analytische Zusammenhang zwischen den Massenwerten und den numerischen Werten der in den Integralen (279) und (284) auftretenden Grössen Ni, gi, βi, der durch die beiden Säkulardeterminanten (281) und (286) führt, ein überaus komplizierter ist, Zur Beantwortung der gestellten Frage stehen uns zwei andere Wege offen. Der eine derselben ist, sich diesbezüglich auf das Urteil eines so erfahrenen Rechners, wie es Leverrier war, zu stützen. Leverrier hat in der Addition III seiner erwähnten Arbeit die numerischen Werte der Elemente e, Ω, i, Π der Erdbahn für jedes zehnte Jahrtausend und für das Zeitintervall von 100.000 Jahren vor und nach 1800 n. Chr. mitgeteilt, wobei er e auf 0,0001, i auf Bogensekunden und Ω auf Bogenminuten genau angegeben betrachtet. Diese Genauigkeit ist mindestens zehnmal so gross als die oben geforderte, woraus sich der Schluss ergeben würde, dass, wenn man sich mit der für geologische Zwecke hinreichender Genauigkeit zufriedenstellt, der Anwendungsbereich der Leverrierschen Berechungen auf eine Million von Jahren vor und nach der Gegenwart bewertet werden kann.
Der andere Weg, diesen Bereich einzuschätzen, gelangt später zur Sprache, da es vorher notwendig ist, die an die Leverrier′schen bzw. die Stockwell′schen Arbeiten anschliessenden numerischen Berechnungen der zeitlichen Aenderungen der Elemente ε, e, Πγ zu besprechen.
Die erste auf einen langen Zeitraum sich erstreckende Berechnung der zeitlichen Aenderungen der Elemente ε, e, Πγ hat Ludwig Pilgrim in seiner Abhandlung "Versuch einer rechnerischen Behandlung des Eiszeitenproblems. Jahreshefte für vaterlündische Naturkunde in Württemberg. Jahrg. 1904. Band 60." geliefert. Diese Arbeit, deren klimatologischer Teil als misslungen zu betrachten ist, zeichnet sich von den vielen damaligen Arbeiten, die sich mit dem Eiszeitenproblem befassten, schon dadurch vorteilhaft aus, dass Pi1grim dieses Problem mit Hilfe der Himmelsmechanik zu lösen versuchte. In dieser Wissenschaft war er gut bewandert, auch habe ich ihn bei der Abfassung meiner Doktorsdissertation als einen guten Rechner kennen gelernt. In seiner oben erwähnten Abhandlung hat er die säkularen Aenderungen der Elemente Πγ, e, ε für jedes fünfte Jahrtausend und für alle jene Zeitpunkte, zu welchen Πγ gleich 90° oder gleich 270° ist, für den Zeitraum von 1.0l0.000 Jahren vor und 40.000 Jahren nach 1850 n. Chr. mit Benützung der Stockwellschen Integrale berechnet. Die Ergebnisse dieser mühsamen Arbeit, die ich anlässlich meiner ersten Berechnungen des säkularen Ganges der Erdbestrahlung benützt habe, gebe ich, soweit sie sich auf die letztverflossenen 1.000 Jahrtausende beziehen, in der nachstehenden Tabelle VIII wieder, weil die Originalarbeit Pilgrims heute schwer aufzutreiben ist.
Meine auf Grund der in der Tabelle VIII mitgeteilten Zahlen durchgeführte und im Köppen-Wegenerschen Werke "Die Klimate der geologischen Vorzeit" veröffentlichte Berechnung des säkularen Bestrahlungsganges der geographischen Breiten von 55°, 60° und 65° nördlich hat, wie noch berichtet werden wird, ausgiebige Anwendung gefunden, weshalb ich mich bei der Abfassung meiner "Mathematischen Klimalehre" entschloss, diese Berechnung auch auf die übrigen geographischen Breiten auszudehnen. Vor Inangriffnahme dieser Arbeit besprach ich diese Angelegenheit mit meinem Kollegen Professor V. Michkovitch, dem vortrefflichen Direktor des astronomischen Observatoriums der Universität in Belgrad. Ich wünschte meine Rechnung des säkularen Ganges der Erdbestrahlung auf solche Berechnungen der säkularen Aenderungen der astronomischen Elemente anschliessen, denen die gegenwärtig als die zuverlässigst anerkannten Werte der Massen der Planeten zugrunde gelegt wären. Die Berechnungen von Leverrier und Stockwell entsprachen nicht dieser Forderung, wie dies aus der nachstehenden Zusammenstellung folgt, in der die reziproken Werte der mit der Sonnenmasse gemessenen Massen der Planeten veranschaulicht sind, wie sie von Leverrier bzw. Stockwell bei ihren Berechnungen Verwendung fanden und wie sie gegenwärtig in den neuesten Jahrgängen der "Connaissance des Temps" angegeben werden.
| Leverrier | Stockweil | Conn. d. Temps | |
| Merkur | 1.909.706 | 4.865.751 | 6.000.000 |
| Venus | 401.839 | 390.000 | 408.000 |
| Erde + Mond | 356.354 | 368.689 | 329.390 |
| Mars | 2.680.337 | 2.680.637 | 3.093.503 |
| Jupiter | 1.050 | 1.047,88 | 1.047 |
| Saturn | 3.512 | 3.501,6 | 3.501 |
| Uranus | 17.918 | 24.905 | 22.869 |
| Neptun | 14.400 | 18.780 | 19.380 |
Sowohl Leverrier als Stockwell haben in ihren Arbeiten die Möglichkeit einer Korrektur ihrer Berechnungen mittels besserer Massenwerte geschaffen und Formeln mitgeteilt, mittels welcher diese Korrektur zu bewerkstelligen wäre. Mein Kollege und ich standen also vor der Frage, an wessen Berechnungen diese Korrekturen durchzuführen wären, an den Leverrierschen oder den Stockwellschen. Unsere Wahl fiel auf Leverrier; die Gründe dafür waren die folgenden. Ein Vergleich der Arbeiten dieser beiden Astronomen ergab, dass die Leverriersche Arbeit jener von Stockwell, in der viele Druckfehler bemerkt und manche kleinere Rechenfehler entdeckt wurden, an Güte überlegen ist. Dies hat bereits Harzer erkannt. Ein weiterer und ausschlaggebender Grund sprach für die Benützung der Leverrierschen Arbeit. Ich habe, wie bereits erwähnt, meine ersten Berechnungen des säkular Ganges der Erdbestrahlung an die Stockwellsche Arbeit angeschlossen, weil die Rechnungen von Pi1grim mir dies ermöglichten. Eine neue Berechnung dieses Bestrahlungsganges, die in Anschluss an die Leverriersche Arbeit, an der man die Massenkorrekturen vornehmen würde, durchgeführt worden wäre, böte eine willkommene Kontrolle der Rechnungsergebnisse von Leverrier und Stockwell und gäbe die Möglichkeit den Einfluss der diesen zwei Arbeiten zugrunde gelegten verschiedenen numerischen Werte der Planetmassen auf den Gang der Erdbestrahlung zu erkennen und dadurch den Anwendungsbereich dieser Rechnungen abzuschätzen.
Kollege Michkovitch übernahm es in dankenswerter Weise, an den Leverrierschen Integralen die erforderlichen Massenkorrekturen vorzunehmen und den zeitlichen Verlauf der säkularen Aenderungen der Elemente ε, e, Πγ für das Zeitintervall der letztverflossenen 600 Jahrtausende zu berechnen. Die Ergebnisse dieser Berechnungen von Michkovitchh habe ich in meiner "Mathematischen Klimalehre&quoT, und in meinen "Astronomischen Mitteln" veröffentlicht und teile sie auch hier in der beiliegenden Tabelle IX mit. Weil, wie noch gezeigt werden wird, in den von mir abgeleiteten Formeln, die der Berechnung des säkularen Verlaufes der Erdbestrahlung dienen, die Elemente e und Πγ immer zusammen und nur in der Kombination e · sin Πγ vorkommen, sind in der Tabelle IX die Aenderungen der Grössen ε und e · sin Πγ gegenüber ihrem Initialwert angegeben. Als Initialmoment ist dabei der Zeitpunkt 1800,0 zu betrachten, dem die folgenden Werte entsprachen:

|
Die Tabelle IX habe ich zur Berechnung der in meinen erwähnten beiden Schriften mitgeteilten Aenderungen der Bestrahlung benützt. Unlängst hat mich Dr. von Bacsak, der diese Tabelle noch einmal überprüfte, auf zwei auf das Glied Δ(e · sin Πγ) und die Zeitpunkte 500 und 465, von welchen der erste in die lnterglazialzeit Günz - Mindel, der zweite in die Interstadialzeit Mindel I - Mindel II fällt, sich beziehende Rechen- oder Schreibfehler aufmerksam gemacht; ich habe sie hier ausgemerzt. Eine Korrektur der hier aus meinen früheren Veröffentlichungen übernommenen graphischen Veranschaulichungen des säkularen Bestrahlungsganges erschien mir nicht notwendig, es genügt der Hinweis auf die zugehörigen Tabellen, in denen diese sonst belanglosen Fehler beseitigt sind.
Meine beiden Berechnungen des säkularen Ganges der Erdbestrahlung, jene mit Benützung der von Stockwell-Pi1grim und jene mit Benützung der von Leverrier-Michkovitch ermittelten Zahlen, ergaben gut übereinstimmende Resultate. Dies ist ein Beweis, dass in den Rechnungen der erwähnten vier Gelehrten gröbere Rechnungsfehler nicht vorkommen; die gegenseitigen Abweichungen rühren von den verschiedenen Massenwerten der Planeten her, die diesen Rechnungen zugrunde lagen. Das Ausmass dieser Abweichungen bezeugt, dass auch weitere durch fernere, bessere Ermittlungen der Planetenmassen sich als notwendig erweisende Korrekturen die wesentlichen Züge des von mir berechneten säkularen Ganges der Erdbestrahlung nicht verändern werden. Um diesbezüglich sicher zu sein, habe ich meine endgültigen Berechnungen des säkularen Ganges der Erdbestrahiung auf das Zeitintervall der letztverflossenen 600 Jahrtausende beschränkt, obwohl man mit einer für geologische Zwecke hinreichenden Genauigkeit wahrscheinlich bis nahe an 1.000 Jahrtausende gehen könnte. Die von Jeffreys (Nature, Vol. 130, 1932) geäusserie Ansicht, der Anwendungsbereich der astronomischen Rechnung reiche über das Zeitintervall von 10 Millionen von Jahren, ist bei dem gegenwärtigen Stande der Wissenschaft leider nicht zutreffend, schon aus dem folgenden Grunde nicht.
Die Störungsrechnung ist auf den Grundmauern der klassischen Mechanik aufgebsut. Diese war trotz aller Bemühungen, an denen sich auch Harzer mit seiner erwähnten Arbeit beteiligt hat, nicht in der Lage, ein Restglied in der Perihelbewegung des Merkurs zu erklären. Dies ist erst der Gravitationstheorie Einstein′s geglückt, nach der nicht nur das Perihel von Merkur, sondern auch die Perihele der übrigen Planeten fortschreitende über die Ergebnisse der klassischen Störungsrechnung reichende Bewegungen vollführen, die in 100 Julianischen Jahren folgende Beträge erreichen:

|
Berücksichtigt man dies, so ergibt es siuch, dass nach Verlauf von einer Million von Jahren sich das Perihel der Erde gegenüber dem Rechnungsergebnis der klassischen Störungsrechnung um l0°39′ verschiebt Diese Verschiebung des Perihels der Erde konnte bei der Berechnung des säkularen Ganges der Erdbestrahlung noch hingenommen werden und zwar aus folgendem Grunde. Die grossen Ausschläge der Erdbestrahlung, jene die die Eiszeiten herursacht hatten, traten, wie noch gezeigt werden wird, in den Zeiten, zu welchen die Länge Πγ des Erdperihels den Betrag von 90° bzw. 270° erreichte. Ist aber Πγ so gross, dann ändert sich sin Πγ bei einer Veränderung von Πγ nur sehr wenig. Ein Fehler in der Länge des Perihels von 10° verursacht dabei in der Rechnung der Erdbestrahlung einen Fehler von 11 kanonischen Einheiten, und dies ist, wie dies aus den noch mitzuteilenden Tabellen der Erdbestrahlung folgt, eine recht kleine Zahl. Bedenklicher sind aber die mit den Perihelbewegungen der Planeten vermittels der Gleichungen (113), (112) und (118) in Zusammenhang stehenden säkularen Aenderungen der Exzentrizität e der Erdbahn und der Schiefe ε der Ekliptik. Ihr Einfluss muss sich bei weiterem Vordringen in die Vergangenheit immer mehr fühlbar machen, um schliesslich die diesbezüglichen Rechnungsergebnisse der klassischen Störungsrechnung über den Haufen zu werfen.
Kapitel XV
Analytische Darstellung des säkularen Ganges der Erdbestrahlung
§ 85. Hilfstabellen zur Berechnung der säkularen Aenderungen der Erdbestrahlung.
§ 86. Allgemeines über den säkularen Gang der Erdbestrahlung. Die Ergebnisse der Tabellen XII und XIII, die ich bereits im Jahre 1914 veröffentlichte, sind von grundlegender Bedeutung, weil durch dieselben zum ersten Male der Einfluss einer Aenderung der Ekliptikschiefe auf den Bestrahlungzustand der Erde in allen seinen Einzelheiten klargelegt wurde. Diese Tabellen zeigen, dass sich die Aenderungen der Ekliptikschiefe an verschiedenen geographischen Breiten verschieden fühlbar machen. Durch einen Zuwachs der Ekliptikschiefe werden die jährlichen Bestrahlungen WT der äquatorialen Zone etwas vermindert, jene der polaren Zonen nicht unwesentlich vergrössert. Die Grenze zwischen diesen Gebieten der jährlichen Bestrahlungszunahme bzw. Abnahme liegt bei 43° 39′. Die halbjährigen Strahlungsmengen Ws und Ww zeigen ein anderes Verhalten. Die sommerlichen Strahlungsmengen Ws werden bei einer Zunahme der Ekliptikschiefe nur bis zur Breite von ll° 23′ vermindert, sonst vergrössert; die winterlichen Strahlungsmengen Ww werden durch einen Zuwachs der Ekliptikschiefe an allen Breiten vermindert. Die prozentuelle Aenderung der sommerlichen Bestrahlung erreicht ihr Maximum an den Polen, jene der winterlichen an der Breite von 66°, wo ein Zuwachs der Ekliptikschiefe von einem Bogengrad eine Verminderung der Grösse Ww von 5,86 Prozent zur Folge hat.
Die in der Tabelle XIII mitgeteilten Aenderungen ΔWs, ΔWw, ΔWT stellen die in Prozenten ausgedrückten Bruchteile der an der oberen Grenze der Atmosphäre anlangende Strahlungsmengen Ws, Ww, WT dar. Wie im nächsten Abschnitt dieses Buches gezeigt werden wird, werden durch Reflexion in der Atmosphäre und an der Erdoberfläche fast 40 Prozent dieser Strahlungsmengen in den Weltraum unbenützt zurückgewiesen und gehen für den Wärmehaushalt der Erde verloren, so dass bloss 60 Prozent, d. h. drei Fünftel dieser Strahlungsmengen den Temperaturzustand der Erdoberfläche und der Erdatmosphäre bestimmen. Weil die durch die astronomischen Ursachen zustande kommenden Bruchteile ΔWs, ΔWw, ΔWT der Strahlungsmengen Ws, Ww, WT vor dem Eintritt der Sonnenstrahlung in die Atmosphäre in Abzug zu bringen sind, hat man, wenn man die Grössen ΔWs, ΔWw, ΔWT in Prozenten der für den Wärmehaushalt der Erde zur Verwendung gelangenden Strahlung ausdrücken will, die in Tabelle XIII mitgeteilten Zahlen mit 5 ⁄ 3 zu multiplizieren, wodurch die Aenderungen der Ekliptikschiefe zu einer höheren Bedeutung gelangen. Diese Aenderungen machen sich, wie aus der Tabelle XIII ersichtlich, besonders fühlbar an den hohen Breiten der Erde. Hier liegt aber der erwähnte durch Reflexionen erlittene Verlust der in die Atmosphäre eindrigenden Strahlung wegen des schieferen Auffallen derselben über dem oben angegebenen Durchschnittswert von 40 Prozent, wodurch die Wirkung der Aenderungen der Ekliptikschiefe noch deutlicher zum Ausdruck gelangt.
Die bisherigen Ergebnisse ermöglichen, einen allgemeinen Ueberblick über den Verlauf des säkularen Ganges der Erdbestrahlung zu gewinnen. Ziehen wir zu diesem Zwecke zuerst die säkularen Aenderungen der Strahlungsmengen Ws, Ww, WT in Betracht. In den Formeln (100) bis (104), durch welche diese Grössen mathematisch veranschaulicht sind, sind von den säkular veränderlichen astronomischen Elementen e, ε, Πγ, nur die ersten zwei enthalten. Dabei kommt die Exzentrizität e der Erdbahn nur im Faktor 1 ⁄ √(1 - e2) vor. Berücksichtigt man, dass e während des Zeitraumes der geologischen Vorzeit, auf den sich meine Untersuchungen beziehen werden, zwischen den Grenzen 0.0051 und 0,0475 schwankt, so findet man, dass sich die Grössen Ws, Ww, WT durch die Veränderlichkeit von e gegenüber ihrem gegenwärtigen Wert nur um 0,013 Prozent vermindern und um 0,099 Prozent erhöhen können. Diese Aenderungen sind derart geringfügig, dass man sagen kann: Die halbjährigen und die ganzjährigen Strahlungsmengen Ws, Ww, WT werden nur durch die Aenderungen der Ekliptikschiefe merklich getroffen.
Wie die Aenderungen der Ekliptikschiefe e in den Gtössen Ws, Ww, WT und an den verschiedenen Breiten zum Ausdruck gelangen, ist, wie bereits gesagt, aus den Tabellen XII und XIII zu ersehen. Eine Zunahme der Ekliptikschiefe vermindert die jährlichen Bestrahlungen WT der äquatorialen Gegenden und vergrössert jene der polaren, d, h. sie vermindert die geographischen Gegensätze zwischen dem Aequator und den Polen. Es lässt sich berechnen, dass bei einer Schiefe von 54° diese Gegensätze vollständig verschwinden in dem Sinne, dass die jährliche Bestrahlung der Pole gleich derjenigen des Aequators wird. Eine Abnahme, der Ekliptikschiefe hat die entgegengesetzte Wirkung, sie verschärft die geographischen Gegensätze, die bei verschwindender Ekliptikschiefe ihr Maximum erreichen, weil dann die beiden Pole während des ganzen Jahres unbestrahlt bleiben.
Hinsichtlich der Grössen Ws und, Ww ist noch folgendes zu sagen. Sieht man von dem tropischen Gürte1 zwischen 11° 23′ nördlich und südlich ab, an dem auch keine ausgeprägten Gegensatze zwischen Sommer und Winter existieren, so ist die Zunahme der Ekliptikschiefe mit einer Vergrösserung der sommerlichen Strahlungsmengen Ws und mit einer Verminderung der winterlichen Strahlungsmengen Ww verbunden, Anders gesprochen: die Zunahme der Ekliptikschiefe verschärft die Gegensätze zwischen Sommer und Winter, die Abnahme der Ekliptikschiefe mildert sie ab. Bei verschwindender Ekliptikschiefe hätte man überhaupt keine Jahreszeiten mehr.
Das bisherige in einem Satz zusammenfassend, kann behauptet werden: Eine Zunahme der Ekliptikschiefe vermindert die geographischen und verschärft die jahreszeitlichen Gegensätze der Erdbestrahlung.
Aus (99) folgt, dass sich die Aenderungen der Ekliptikschiefe auf beiden Hemisphären der Erde in ganz gleicher Weise fühlbar machen, d. h. die obigen Gegensätze werden auf beiden Hemisphären zu gleicher Zeit vermindert bzw. verstärkt.
Wie die Aenderungen der Ekliptikschiefe während der letzverflossenen Million von Jahren verlaufen sind, ist aus der Tabelle VIII deutlich ersichtlich. Nach dem darin vorkommenden ersten Maximum der Ekliptikschiefe, das im Jahrtausend 980 stattfand, bis inklusive dem letzten, das im Jahrtausend 10 vor der Gegenwart erreicht wurde, hat die Schiefe der Ekliptik 24 solcher Maxima und ebensoviel Minima erreicht. Der zeitliche Abstand zwischen zwei aufeinander folgenden Maxima betrug fast durchwegs rund 40 Jahrtausende, sank einmal auf fast 38 und erreichte zweimal die Länge von 45 Jahrtausenden. Der Rhythmus der Schwankungen der Ekliptikschiefe war also ein ziemlich regelmässiger, nicht so die Amplitude der Schwankungen. Das grösste der Maxima betrug 24° 28′, das kleinste 23° 40′; das kleinste der Minima 22° 0′, das grösste 22° 57′. Der deutlich oszillatorische Charakter der Aenderungen der Ekliptikschiefe blieb dabei unverkennbar.
Wenn bloss diese Aenderungen der Ekliptikschiefe im Spiele wären, würden bei jedem Maximum der Ekliptikschiefe die geographischen Gegensätze auf beiden Hemisphären ihr Minimum, die jahreszeitlichen ihr Maximum erreicht haben, das entgegengesetzte bei jedem Minimum der Ekliptikschiefe stattfinden. Diese Erscheinungen würden sich im verschieden starken Ausmasse alle 20 Jahrtausende abwechselnd wiederholen, wenn nicht die Veränderlichkeit der übrigen zwei astronomischen Elemente dazwischenträte.
Die wichtigsten Merkmale des Bestrahlungszustandes der Erde sind durch die den einzelnen Breiten zugestrahlten Wärmemengen Ws und Ww nicht erschöpft, es kommt auch darauf an, während welcher Zeitintervalle diese Mengen zugestrahlt werden. Diese Zeitintervalle, das astronomische Sommerhalbjahr und das astronomische Winterhalbjahr, sind, wie dies aus den Gleichungen (88), f89), (Ill) folgt, Funktionen der zwei übrigen astronomischen Elemente, der Exzentizität e der Erdbahn und der Länge Πγ des Perihels. Aus den erwähnten Gleichungen folgt die Formel:
| (125) |

|
durch die die Differenz der astronomischen Jahreszeiten Ts und Tw veranschaulicht erscheint. Um einen ersten Einblick in die säkularen Aenderungen dieser Grösse zu gewinnen, ziehen wir abermals die Tabelle VIII zu Rate. Aus derselben ist vor allem ersichtlich, dass während des durch die Jahrtausende 986,2 und 0 0,6 vor der Gegenwart gekennzeichneten Zeitintervalles die Länge Πγ des Perihels um 47 · 360°, d. h. während einer Zeitspanne von durchschnittlich 21.000 Jahren um 360° zugenommen hat. Diese Zunahme war aber nicht gleichmässig, die Perihellänge nahm manchmal schon während der Zeitspanne von 16,3 Jahrtausenden, mitunter erst während einer solchen von 25,8 Jahrtausenden um 360° zu. Diese Unregelmässigkeiten in der Zunahme der Perihellänge haben ihren Ursprung im folgenden.
Die Gleichung (112) lehrt, dass die Länge Πγ des Perihels in bezug auf den jeweiligen, Frühlingspunkt gleich ist der Länge Π des Perihels in bezug auf den fixen Frühlingspunkt und der allgemeinen Präzession Ψ′.
Die allgemeine Präzession unterscheidet sich von dem permanenten Bestandteil der lunisolaren Präzession durch die periodischen Glieder, die von den Schwankungen der Erdbahnebene und der Erdachse herrühren. Diese periodischen Glieder sind recht klein, so dass man, ohne die Genauigkeit der Rechnung des säkularen Ganges der Erdbestrahlung wesentlich einzuschränken, die allgemeine Präzession als der Zeit proportional annehmen könnte. Die erwähnten und aus der Tabelle VIII ersichtlichen Unregelmässigkeiten in der Zunahme der Grösse Πγ rühren von dem Gliede Π der Gleichung (112) her. Die säkularen Aenderungen der Grösse Π, die durch die Gleichungen (113) gegeben sind, weisen einen ziemlich unregelmässigen Verlauf auf, wie dies aus den Berechnungen von Leverrier-Michkovitch bzw. Stockwe1l-Pilgrim folgt und auch aus einer graphischen Veranschaulichung dieser Aenderungen, die Char1ier geliefert hat, ersichtlich ist. Wie bereits im § 82 erwähnt, eilt die grosse Achse der Erdbahnellipse der Frühlingslage der Erde entgegen, weshalb der Umlauf derselben um die Erdbahn nicht 26.000 Jahre, sondern weniger erfordert. Dies gilt mit kurzen Unterbrechungen für das Zeitintervall, auf das sich die bisherigen Berechnungen der säkularen Aenderungen der Grösse Π erstrecken. Ob dies auch für alle Zeiten gültig ist, d. h. ob das Perihel der Erdbahn die im § 22 besprochene. mittlere Bewegung besitze, ist eine offene Frage, weil keiner der Koeffizienten N1, N1, ... Nn der Gleichungen (113) seinem absoluten Werte nach die Summe der absoluten Werte der übrigen Koeffizienten übersteigt.
Auch die säkularen Aenderungen der Exzentrizität e der Erdbahn sind bei weitem nicht so regelmässig wie jene der Schiefe der Ekliptik. Sie weisen zwar, wie dies aus der Tabelle VIII und dem der Pilgrimschen Abhandlung beigefügten Graphikon folgt, ebenfalls einen oszillatorischen Charakter auf, doch sind .die Perioden und Amplituden der einzelnen Oszillationen recht verschieden. Nach dem ersten in der Tabelle VIII vorkommenden Maximum der Exzentrizität der Erdbahn, das im Jahrtausend 935 stattfand, folgten bis zum Jahrtausend 15 vor der Gegenwart 10 weitere Maxima, so dass die durchschnittliche Periode dieser Oszillationen 92 Jahrtausende betrug; die tatsächlichen Periode variierten zwischen 77 und 103 Jahrtausenden. Das grösste der erreichten Maxima betrug 0,0655, das kleinste 0,0221; das kleinste der Minima betrug 0,00l8, das grösste 0,00199. Die mit der Formel (239) des ersten Abschnittes dieses Buches ermittelte obere Grenze der Exzentrizität der Erdbahn liegt nach den Berechnungen von Stockwe11 bei 0,067735, nach jenen von Michkovitch bei 0,063865.
Die soeben geschilderten säkularen Aenderungen der Elemente Πγ und e machen sich im säkularen Gange der Erdbestrahlung folgenderweise geltend.
Schliesst man den Fall e = 0 aus, weil er während der in Betracht zu ziehenden Spanne der geologischen Vorzeit nicht vorgekommen ist, dann verschwindet die Differenz Ts - Tw nur wenn Πγ, gleich 0° oder 180° wird. Nimmt Πγ von O° bis 90° zu, so wird das Sommerhalbjahr der nördlichen Hemisphäre auf Kosten des Winterhalbjahres immer länger und länger, so dass, wenn man die Aenderungen der Ekliptikschiefe vorläufig ausser Acht lässt, die unveränderte, Strahlungsmenge W, auf immer längere und längere Zeitintervalle aufgeteilt wird und die durchschnittliche, pro Zeiteinheit berechnete, sommerliche Bestrahlung von Jahr zu Jahr abnimmt. Das umgekehrte gilt für den Winter; derselbe wird kürzer, seine durchschnittliehe Bestrahlung intensiver. Dies gilt im gleichen Masse für alle Breiten der Hemisphäre.
Hat Πγ den Wert von 90° erreicht, so ist die Länge des Sommerhalbjahres sehr nahe ihrem Maximum, das wegen der Veränderlichkeit von e nicht ganz genau mit Πγ = 90° zusammenfällt, d. h. die durchschnittliche sommerliche Bestrahlung ist bis zu ihrem Minimum gesunken, die winterliche bis zu ihrem Maximum gestiegen. Die jahreszeitlichen Gegensätze sind auf ein Minimum gesunken.
Dies gilt aber nur für die nördliche Hemisphäre. Auf der südlichen Hemisphäre hat das Sommerhalbjahr, das mit dem Winterhalbjahr der nördlichen Hemisphäre zusammenfällt, sein Maximum erreicht, während die Quantitäten der Sonnenstrahlung Ws, die den südlichen Breiten während dieses kurzen Sommers zugestrahlt werden, gleich jenen sind, welche die nördlichen Breiten während des langen nördlichen Sommers empfangen. Auf der südlichen Hemisphäre wird a1so der Sommer kurz und warm, der Winter lang und kalt. Zu den Zeiten, in welchen die jahreszeitlichen Gegensätze auf der nördlichen Hemisphäre ihre grösste Abmilderung erfahren, erreichen sie auf der südlichen ihre grösste Verschärfung.
Hat Πγ den Wert von 180° erreicht, so sind die Jahreszeiten Ts und Tw einander gleich und die beiden Hemisphären sind gleichgestellt.
Bei Πγ = 270° ist die Länge des nördlichen Sommerhalbjahres auf ein Minimum gesunken, jene des Winterhalbjahres hat ein Maximum erreicht, die jahreszeitlichen Gegensätze haben ihre grösste Verschärfung erfahren. Auf der südlichen Hemisphäre sind diese Gegensätze, bei einem langen, kühlen Sommer und kurzem, milden Winter, möglichst abgeschwächt.
Bei Πγ = 360° sind beide Hemisphäre, bei gleichen Jahreszeiten Ts und Tw vollkommen gleichgestellt und das Spiel beginnt in der oben beschriebenen Weise von neuem, mit dem Unterschied, dass wegen der Veränderlichkeit von e die jahreszeitlichen Gegensätze der nachfolgenden Periode, während welcher Πγ wieder von 0° bis 360° zunimmt, nicht jenen der vorhergehenden Periode gleich sein werden, sondern während des Zeitintervalles, während welchem e zunimmt, sich noch ausgesprochener verschärfen bzw. abmildern werden, um während der nachfolgenden Zeitdauer, bei abnehmendem e etwas zu erblassen.
Die soeben geschilderten, von den Grössen e und Πγ herrührenden Aenderungen des jährlichen Bestrahlungsganges werden sich mit jenen durch die Variabilität der Grösse e hervorgerufenen überlagern. Diese letzteren haben, wie gezeigt, eine andere Periode und machen sich auf beiden Hemisphären im gleichen Sinne, aber an verschiedenen Breiten in verschiedenem Masse fühlbar.
Durch die Ueberlagerung dieser beiden Arten der säkularen Aenderungen des jährlichen Bestrahlungsganges geht die einfache Gesetzmässigkeit verloren, die jeder dieser Arten eigen ist.
§ 87. Die kalorischen Jahreszeiten.
§ 88. Die den kalorischen Jahreszeiten der einzelnen Breiten zugehörigen Zeitintervalle.
§ 89. Die während der kalorischen Jahreszeiten den einzelnen Breiten zugestrahlten Wärmemengen.
§ 90. Der kalorische Aequator.
§ 91. Analytische Darstellung des säkularen Bestrahlungsganges der einzelnen Breiten der Erde.
§ 92. Analytische Darstellung des säkularen Bestrahlungsganges einzelner Zonen der Erdoberfläche.
§ 93. Analytische Darstellung des säkularen Ganges der durchschnittlichen Bestrahlung der nördlichen bzw. der südlichen Hemisphäre der Erde.
Fünfter Abschnitt
Zusammenhang zwischen Einstrahlung und Temperatur der Erde und ihrer Atmosphäre
Das mathematische Klima der Erde
Kapitel XVI
Einleitung. Grundlegende Tatsachen und Gesetze
§ 94. Das mathematische Klima der Erde. Das, was man unter Klimatologie allgemein versteht, ist die Erforschung und Beschreibung des mittleren Zustandes und gewöhnlichen Verlaufes der Witterung an den verschiedenen Orten der Erdoberfl6#228;che. Die erforderlichen Daten zu dieser Beschreibung werden durch langjährige direkte Beobachtungen gewonnen, die nach statistischen Methoden verarbeitet werden. Deshalb ist die Klimatologie nach ihrem gegenwärtigen Stand eine empirische beschreibende Wissenschaft. Die Meteorologie ist bestrebt, die beobachteten Witterungserscheinungen durch physikalische Gesetze zu erklären, um auf diese Weise den Zusammenhang zwischen den klimatischen Erscheinungen und ihren Ursachen aufzudecken. Der dabei betretene Weg ist ein induktiver: man geht von der Erforschung der einzelnen örtlich und zeitlich begrenzten Tatsachen aus, versucht diese zu systematisieren und zu einem Ganzen zusammenzufügen. Es ist dies das natürliche Anfangsstadium im Werdegange einer Wissenschaft. Die exakten Naturwissenschaften haben dieses Anfangsstadium schon längst überschritten und sind imstande, durch allgemein geltende Gesetze auch alles einzelne zu erfassen. Weil die Meteorologie dieses Stadium noch nicht erreicht hat, sträuben sich manche Syslematiker noch immer, sie als eine ausgebildete Wissenschaft anzuerkennen.
Man kann jedoch, wie ich dies im Vorwort dieses Buches ausführlich auseinandergesetzt habe und wie dies aus den nachstehenden Ausführungen folgen wird, auch in der Klimalehre den deduktiven Weg betreten, um aus der Intensität der Sonnenstrahlen und aus allgemeinen das Weltall beherrschenden Gesetzen die Grundzüge der thermischen Erscheinungen auf der Erdoberfläche und in der Atmosphäre abzuleiten, Dieses theoretisch errechnete Klima der Erde wird das "mathematische Klima" genannt. Diesen theoretisierenden Teil der Klimatologie habe ich in meiner "Mathematischen Klimalehre", die den einleitenden Hauptartikel des Köppen-Geigersehen Handbuches der Klimatologie bildet, zu einem vorläufigen Abschluss gebracht. Die dort niedergelegte Theorie ist wohl eines weiteren Ausbaues fähig, wie dies sogleich dargelegt werden soll
In meiner "Mathematischen Klimalehre" mussten, wie es beim Aufbau jeder mathematischen Theorie der Fall ist, gewisse vereinfachende Voraussetzungen gemacht werden, um die zu beschreibenden Naturerscheinungen durch Differentialgleichungen zu erfassen und diese integrieren zu können. Die wichtigsten dieser Annahmen sind die folgenden. Die Erdoberfläche wird als vollkommen eingeebnet, das Material der äussersten am Wärmeaustausch teilnehmenden Schicht der Erdkruste als homogen vorausgesetzt. Die der Schwerkraft und den Gesetzen für vollkommene Gase unterworfene Atmosphäre befindet sich in einem mittleren Bewölkungszustand, ihre Konstitution ist nur eine Funktion der Höhe über der Erdoberfläche. Die in die Atmosphäre eindringende Sonnenstrahlung, die Ausstrahlung der Erdoberfläche und die dunkle Strahlung der Atmosphäre gehorchen dem kombinierten Kirchhoff-Stefanschen Gesetz. Der Wärmeaustausch zwischen der Erdoberfläche und der Atmosphäre erfolgt nur durch Strahlung. Die durch die Störung des mechanischen Gleichgewichts in der Atmosphäre und in der Hydrosphäre entstehenden Strömungen werden nicht berücksichtigt.
Von allen diesen Annahmen ist die zuletzt angeführte die schwerwiegendste, weil durch dieselbe ein ganzer Komplex meteorologischer Erscheinungen aus dem Bereich meiner Untersuchungen ausgeschieden erscheint und das von mir berechnete Klima, im Grunde genommen, dem sogenannten "solaren Klima" entspricht, worunter jenes Klima zu verstehen ist, welches nur von der Quantität der Sonnenstrahlung abhängt, die einem Ort nach seiner geographischen Breite zukommt.
Trotz dem sollen das mathematische Klima und das solare Klima auseinandergehalten werden. Sie decken sich in vorliegendem Falle wegen der Annahmen, die der Theorie zugrunde lagen. Es ist wohl nur eine Frage der Ueberwindung analytischer Schwierigkeiten die durch die Strahlungserscheinungen auf die Meridianebenen sich beschränkenden Störungen des mechanischen Gleichgewichts zu berücksichtigen und die vorliegende Theorie in dem Sinne zu erweitern, dass in derselben die durch jene Störungen und die ablenkende Kraft der Erdrotation hervorgerufenen Zirkulationen der Atmosphäre zum Ausdruck gelangen, wobei man anfangs den durchschnittlichen jährlichen Bestrahlungszustand der einzelnen Breiten der Rechnung zugrunde legen wird, um einen stationären Bewegungszustand vor sich zu haben, und um erst nachher auf den periodischen Bestrahlungszustand zu übergehen. Ein solcher Vorgang wird auch nachstehend beim statischen Zustand der Atmosphäre zur Anwendung gelangen.
In den ersten vier Abschnitten dieses Buches wurden die für die Ziele desselben aus dem Newtonschen Gravitationsgesetz und aus dem Bestrahlungsgesetz sich ergebenden Schlussfolgerungen gezogen. Diese Abschnitte bilden den astronomischen Teil des Werkes. Im vorliegenden Abschnitt müssen auch einige physikalische Gesetze herangezogen werden, weshalb derselbe als der physikalische Teil des Werkes bezeichnet werden kann. Mit diesen Gesetzen müssen wir uns vorerst vertraut machen.
§ 95. Die Schichtung der Atmosphäre.Die Atmosphäre der Erde ist ein Gemisch von verschiedenen vollkommenen Gasen und Wasserdampf. Diese Gase, dem Gravitationsfelde der Erde unterjocht, gehorchen überdies dem Dalton′schen Gesetz, nach dem der Partialdruck jedes einzelnen Gases in der Atmosphäre von der Anwesenheit der übrigen Gase unabhängig ist. Man kann deshalb jedes dieser Gase für sich behandeln; die Sonderstellung des Wasserdampfes soll später berücksichtigt werden.
Man nehme also vorläufig an, die zirkulationslos gedachte Atmosphäre der Erde bestehe nur aus einem einzigen Gas, für das die Zustandsgleichung
| (1) | v · p = R · Θ, |
genannt das Boyle-Charles′sche oder das Mariotte-Gay Lussac′sche Gesetz, gilt. In derselben bedeutet v das Volumen der Masseneinheit, p den Gasdruck, Θ die absolut gemessene Gastemperatur und R die sogenannte Gaskostante, die von der Natur des Gases abhängig, ist, Bezeichnet ρ die Dichte der Atmosphäre, d. h. die Masse der Volumseinheit, so ist
| ρ = 1 ⁄ v, |
so dass es wird
| (2) | p = R · Θ · ρ. |
In einer vertikalen an der in Betracht gezogen Stelle der Erdoberfläche sich erhebenden Luftsäule sind die Grössen p, Θ, ρ Funktionen der von der Erdoberfläche gemessenen Entfernung x, so dass die vorstehende Gleichung die Form erhält:
| (3) | p(x) = R · Θ(x) · ρ(x). |
Das spezifische Gewicht der Atmosphäre an der Stelle x ist gleich :
| (4) | δ(x) = g(x) · ρ(x), |
worin g(x) die Beschleunigung der Schwere an der Stelle x bedeutet. Bezeichnet man die Beschleunigung der Schwere an der in Betracht gezogenen Stelle der Erdoberfläche mit g und nimmt man auf die unbedeutende innere Gravitation der Atmosphäre keine Rücksicht, so ist nach dem Newtonschen Gravitationsgesetz.

|
wovon r den Radius der Erdkugel bedeutet. Es ist also:
| (5) |

|
Erhebt man sich längs der Vertikalen um die Strecke dx, so nimmt der Gasdruck um
| (6) |

|
zu [ab!], weil mit zunehmender Höhe der auf die Flächeneinheit wirkende Druck in dem Masse abnimmt, in dem sich das über dieser Flächeneinheit lastende Gewicht verringert.
Die Differentiation von (3) ergibt:

|
d. h. wegen (6) und (5):

|
Diese Gleichung veranschaulicht den Zusammenhang zwischen Dichte, Temperatur und Höhe x. Man kann derselben, wenn man berücksichtigt, dass die praktisch fühlbare Höhe der Atmosphäre im Vergleich zum Radius r der Erdkugel sehr klein ist, also x neben r vernachlässigt werden kann, die einfachere Form geben:<
| (7) |

|
Hätte man noch eine Gleichung zwischen den Grössen Θ, ρ und x, so wäre man in der Lage, die analytischen Ausdrücke der Funktionen ρ(X) und Θ(x) abzuleiten. Diese hier noch fehlende Gleichung wird später aus den Strahlungsgesetzen gewonnen werden. Vorläufig kann die Funktion ρ(x) dadurch ermittelt werden, dass man auf die Aenderung der Temperatur Θ(x) mit der Höhe x keine Rücksicht nimmt, also Θ(x) als konstant betrachtet und setzt
| Θ(x) = Θ0, |
wobei Θ0 eine von x unabhängige Grösse bedeutet. In einem solchen Falle erhält man statt (7)
| (8) |

|
Setzt man der kürzeren Schreibweise halber
| (9) |

|
so wird

|
Die Integration dieser Differentialgleichung liefert, wenn man die Dichte der Atmosphäre an der Erdoberfläche, d. h. für x = 0, mit ρß, bezeichnet,
| (10) |

|
Diese Formel gibt die Dichteabnahme der isotherm vorausgesetzen Atmosphäre mit der Höhe x an. Eine solche Atmosphäre erstreckt sich theoretisch bis in die Unendlichkeit, praktisch bis zu jener Höhe, in der ρ(x) ernachläässigbar klein wird.
Wendet man die obige Formel für solche Höhenintervalle an, für welche die Temperatur nicht mehr als konstant zu betrachten ist, so kann der aus der Anwendung dieser Formel sich ergebende Fehler teilweise kompensiert werden, wenn man in (9) den Mittelwert der Temperatur der in Betracht gezogenen Luftsäule einsetzt.
Interessant ist die Bedeutung der Grösse H. Um diese zu ersehen, berechne man die Luftmasse der über der Flächeneinheit der Erdoberfläche sich erhebenden Säule der Atmosphäre. Diese ist dargestellt durch:

|
d. h. durch:
| (11) | M = ρ0 · H |
Es stellt also H jene Höhe dar, die die Atmosphäre aufweisen würde, wenn sie auf die Dichte &ß961;0 komprimiert wäre. Diese Grösse wird die virtuelle Höhe der Atmosphäre genannt.
Wird der Atmosphärendruck p(0) an der Erdoberfläche und die Gaskonstante R mit der terrestrischen Krafteinheit, d. h. mit dem Gewicht g der Masseneinheit gemessen und mit p0 bzw. mit R0 bezeichnet, wird also gesetzt:
| (12) |

|
so ist nach (3)
| (13) |

|
| (14) |

|
in welcher Form man die virtuelle Höhe der Atmosphäre gewöhnlich zum Ausdruck bringt.
Die soeben abgeleiteten Beziehungen gelten für jedes vollkommene Gas der Atmosphäre. Bezeichnet man die Dichten dieser einzelnen Gase an der Erdoberfläche mit ρ1, ρ2, ρ3 ... und die ihnen entsprechenden virtuellen Höhen mit H1, H2, H3, ..., so ist die Dichte ρ(x) der aus diesen Gasen gebildeten Atmosphäre durch den Ausdruck dargestellt:
| (15) |

|
Wegen der Verschiedenheit der Grössen HH1, H2, H3, ... werden die Dichten der einzelnen Gase mit der Höhe x in verschiedenem Masse mit der Höhe abnehmen, so dass jedem x ein anderes Mischungsverhältnis der Gase entsprechen wird.
Die Atmosphäre der Erde besteht in ihren unteren Schichten vorwiegend aus Stickstoff und Sauerstoff. Die Konstanten R0 dieser beiden Gase unterscheiden sich wenig voneinander, so dass man nach (14) auch ihre virtuellen Höhen als einander gleich setzen kann. Es wird also H1 = H1 = H, während die Dichte ρ0 der trockenen Luft an der Erdoberfläche durch ρ0 = ρ1 + ρ2 dargestellt ist. Für trockene Luft gilt also die Formel (10) genügend genau.
Bei konstant angenommenem Θ ist nach (3) und (14)

|
d. h. wegen (10)
| (16) |

|
wodurch man zu_ der für die isotherm vorausgesetzte Atmosphäre gültigen barometrisehen Formel gelangt, die die Grundlage fär das barometrische Höhenmessen bildet und in der für Mitteleuropa H = 8.000 m zu setzen ist.
Vorstehend ist die Anwesenheit des Wasserdampfes in der Atmosphäre nicht n Betracht gezogen worden. Der Gehalt desselben ist fortwährenden Aenderungen unterworfen, doch gehorcht sein durchschnittlicher Druck genügend genau der von Hann empirisch gefundenen Formel:
| (17) |

|
in der e den Dampfdruck und p den Luftdruck bedeutet. Weil in einer isothermen Atmosphäre der Druck des ungesättigten Wasserdampfes genügend genau seiner Dichte ρ′ proportional ist, so folgt aus der obigen Formel

|
d. h. wegen (16)
| (18) |

|
welche Formel die Dichteabnahme des Wasserdampfes mit der Hhe H zum Ausdruck bringt. Dabei bedeutet H die virtuelle Höhe der Luftatmosphäre.
Setzt man
| (19) | H′ = H ⁄ 3 |
so bekommet man
| 20 |

|
also eine Gleichung von derselben Form wie (10). Dabei ist zu beachten, dass in (20) H′ nicht die virtuelle Höhe einer Wasserdampfatmosphäre bedeutet; diese ist viel grösser als H′, so dass der Wasserdampf mit der Höhe viel rascher abnimmt als dies aus der Theorie für vollkommene Gase folgen würde.
Aus (20) und (15) folgt, dass diese letztere Gleichung bei Beachtung der vorstehenden Bemerkung für alle Gase der Atmosphäre inklusive Wasserdampf als geltend zu betrachten ist.
§ 96. Das Bouguer-Lambertsche Gesetz.
§ 97. Numerische Ergebnisse.
§ 98. Die Strahlungsbilanz der Erde. Beim Eintritt der Sonnenstrahlen in die Erdatmosphäre erfährt die Energie, die in diesen Strahlen enthalten ist, mannigfaltige Umwandlungen. Die im § 95 besprochene Zunahme der Dichte der Atmosphäre gegen die Erdoberfläche zu hat zur Folge, dass die Sonnenstrahlen von ihrer ursprünglichen Richtung schwach abgelenkt und zum Lot gebrochen werden. Diese Erscheinung, Refraktion genannt und im § 42 besprochen, übt keinen nennenswerten Einfluss auf den Bestrahlungszustand der Erde aus und muss hier nicht berücksichtigt werden.
Eine ungleich wichtigere Beeinflussung der Sonnenstrahlung durch die Atmosphäre besteht darin, dass an den Molekülen der Atmosphäre ein Bruchteil der Sonnenstrahlung nach allen Richtungen reflektiert, ein anderer Bruchteil in die Energie der Moleküle umgewandelt wird, während der Rest als direkte Sonnestrahlung bis zur Erdoberfläche gelangt. Durch diese Beeinflussungen der Sonnenstrahlung, von denen die erste die diffuse Reflexion, die zweite die Absorption genannt wird, wird jedes Molekül der Atmosphäre zum Ausgangspunkt zweier Strahlungen: der diffusen Sonnenstrahlung und der durch den Temperaturzustand des Moleküls bedingten dunklen Strahlung der Atmosphäre. Diese beiden Strahlungen breiten sich von ihrem Ursprunge nach allen Richtungen aus, um schliesslich entweder an die Erdoberfläche oder in den Weltraum zu gelangen. Dabei werden sie auf ihrem Wege durch die Atmosphäre ähnlich wie die direkten Sonnenstrahlen beeinflusst.
Die Oberfläche der Erde wird nach dem soeben gesagten von einer strahlenden Energie getroffen, die aus drei verschiedenen Arten von Strahlungen zusammengesetzt ist: der direkten Sonnenstrahlung, der diffusen Sonnenstrahlung und der dunklen Strahlung der Atmosphäre. Von dieser strahlenden Energie wird ein Teil von der Erdoberfläche zurückreflektiert, um seinen Rückweg durch die Atmosphäre zu nehmen und von derselben, wie bereits geschildert, beeinflusst zu werden; der verbleibende Teil wird von der festen Oberfläche der Erde oder von den dieselbe überlagernden Flüssigkeitsmassen aufgenommen und zu deren Temperaturerhöhung verbraucht. Der Temperaturzustand der Erdoberfläche ruft seinerseits eine dunkle Ausstrahlung der Erdoberfläche hervor, die sich gegen den Weltraum ausbreitet und von der Atmosphäre ähnlich wie die übrigen Strahlungen beeinflusst wird.
Sind in der Atmosphäre Wolkenbildungen enthalten, so werden alle Strahlen, die auf diese Bildungen auffallen, teilweise reflektiert, teilweise durchgelassen und teilweise absorbiert, um die Ursache einer von diesen Wolken ausgehenden Strahlung zu werden.
Es liegt in der Natur der Sache, dass es ungemein schwer ist, die Beeinflussungen, die die Sonnenstrahlung und die dunkle Ausstrahlung der Erdoberfläche durch die Atmosphäre erleiden, quantitativ zu erfassen. Seit der ersten durch die Smithsoniansehe Institution zu Washington erzielten zuverlässigen Ermittlungen der Solarkonstante hat es noch drei Jahrzehnte gedauert, bis man die einzelnen, nach den vor stehend mitgeteiten Gesichtspunkten kategorisierten prozentuellen Bestandteile der Sonnenstrahlung und der Erdausstrahlung, also die Strahlungsbilanz der Erde, mit zufriedenstellender Genauigkeit ermitteln konnte. Als gegenwärtiges Endergebnis dieser langjährigen Bemühungen ist die Strahlungsbilanz von F. Baur und H. Phi1ipps zu betrachten, die eine wohldurchdachte Synthese von Theorie und Erfahrung darstellt. Nachdem diese Forscher vorerst eine in die Einzelheiten reichende theoretische Untersuchung über den jährlichen Gang der Bestrahlung der einzelnen Zonen der nördlichen Hemisphäre und über den Zusammenhang zwischen Einstrahlung und Temperatur durchgeführt hatten, gingen sie daran, aus dem durch die Beobachtungen gegebenen tatsächlichen Temperaturfeld der Atmosphäre die beiden in derselben vor sich gehenden, nach oben und unten gerichteten Strahlungsströme zu ermitteln und zu zergliedern.
Die Ergebnisse der Arbeit von Baur und Phi1ipps sind in der nachstehenden Strahlungsbilanz der nördlichen Hemisphäre zusammengefasst, wobei die einzelnen Strahlungen in Prozenten der an der oberen Grenze der Atmosphäre anlangenden Sonnenstrahlung angegeben sind.
| 1. | Ausseratmosphärische Sonnenstrahlung | 100 |
| 2. | Vom Erdboden absorbierte direkte Sonnenstrahlung | 27 |
| 3. | Vom Erdboden absorbierte indirekte Sonnenstrahlung | 16 |
| 4. | Von den Wolken reflektierte birekte Strahlung | 30 |
| 5. | Von der Erdoberfläche reflektierte direkte Strahlung | 3 |
| 6. | Von der Lufthülle diffus nach dem Weltraum reflektierte Strahlung | 8 |
| 7. | Von der Erdoberfläche reflektierte indirekte Strahlung | 1 |
| 8. | Von der Lufthülle (einschliesslich Wolken) absorbierte Strahlung | 15 |
| Langwellige Strahlung | ||
| 9. | Temperaturstrahlung von der Erdoberfläche ausgehend | 120 |
| 10. | Durchgelassener Tei! der Erdoberflächenstrahlung | 8 |
| 11. | Von der Lufthülle absorbierte langwellige Strahlung | 112 |
| 12. | Von der Lufthülle abgegebene langwellige Strahlung | 146 |
| Von derselben entfallen auf | ||
| 13. | Ausstrahlung | 50 |
| 14. | Gegenstrahlung | 96 |
| Vertikal transportierte Wärme | ||
| 15. | Von der Lufthülle durch vertikalen Austausch abgegebene und vom Erdboden aufgenommene Wärmemenge | 4 |
| 16. | Vom Erdboden durch Verdunstung abgegebene und von der Lufthülle durch Kondensation aufgenommene Wärmemenge | 23 |
In der obigen Zusammenstellung gibt Post 1 die an. der oberen Grenze der Atmosphäre von aussen anlangende Strahlung an; Post 4 (30Ὺ), Post 5 (3Ὺ), Post 6 (8Ὺ), Post 7 (lῪ), Post 10 (8Ὺ) Post 13 (50Ὺ) geben die von unten an die obere Grenze der Atmosphäre anlangerden Strahlungen an; ihre Summe ist gleich 100Ὺ, so dass an der oberen Grenze der Atmosphäre Einnahme und Ausgabe sich die Wage halten.
Post 2 (27Ὺ), Post 3 (16Ὺ), Post 14 (96Ὺ), Post 15 (4Ὺ) geben die dem Erdboden zugeführten, Post 9 (120Ὺ), Post 16 (23Ὺ) die von demselben abgegebenen Strahlungs- bzw. Wärmemengen an. Auch hier sind Einnahme (143Ὺ) und Ausgabe einander gleich.
Post 8 (15Ὺ), Post 11 (l12Ὺ), Post 16 (23Ὺ) geben die von der Atmosphäre aufgenommenen, Post 12 (146Ὺ), Post 15 (4Ὺ) die von der Atmosphäre abgegebenen Wärmemengen an. Auch hier ist Einnahme (150Ὺ) gleich der Ausgabe.
Von der in die Erdatmosphäre eindringenden Sonnenstrahlung werden Post 4 (30Ὺ), Post 5 (3Ὺ), Post 6 (8Ὺ), Post 7 (lῪ), also zusammen 42 Prozent unbenützt in den Weltraum zurückgewiesen. Dieser Bruchteil der Sonnenstrahlung wird die Energiealbedo der Erde genannt. Ich will ihn lieber das Reflexionsvermögen der Erde samt ihrer Atmosphäre nennen und mit A bezeichnen. Nach der vorstehenden Strahlungsbilanz wäre also A = 0,42 zu setzen.
Hinsichtlich des numerischen Wertes des durchschnittlichen Transmissionskoeffizienten der Erdatmosphäre für die direkte und indirekte Sonnenstrahlung ergibt sich aus dem vorstehenden folgendes.
Von der nicht in den Weltraum zurückreflektierten Strahlung, also von den 58 Prozent der an der oberen Grenze der Atmosphäre anlangenden Strahlungsmenge, werden nach Post 8 der vorstehenden Zusammenstellung von der soeben angegebenen Strahlungsmenge 15 Prozent von der Lufthülle absorbiert und 43 Prozent durchgelassen. Dies ist gleich dem Bruchteil x = 43 ⁄ 58 = 0,74 der der Nordhalbkugel zugewiesenen und nicht zurückreflektierten Strahlung. Diesem Bruchteil entspricht nach der vorstehend mitgeteilten Tabelle XV ein für den senkrechten Durchgang durch die Atmosphäre sich ergebende Transmissionskoeffizient pa = 0,84.
Die dunkle Austrahlung der Erdoberfläche ist von der Zenitdistanz der Sonne unabhängig. Weil nach Post 9 und 10 der vorstehenden Zusammenstellung 8 von 120 Einheiten in den Weltraum durchgelassen werden, beträgt der Transmissionskoeffizient der Atmosphäre für die dunkle Strahlung der Erdoberfläche pa′ = 8 ⁄ 120 = 0,067.
Man hätte also, die vorstehenden Zahlen zusammenfassend, für die nördiiche Hemisphäre der Erde zu setzen:
| (37) | A = 0,42 pa = 0,84 pa′ = 0,067. |
Ob und wie diese Zahlen abgeändert werden müssten, wenn man die ganze Erdkugel in Betracht ziehen würde, ist in der Abhandlung von Baur und Phi1ipps nicht angegeben.
Zur Zeit, als ich in meiner "Théorie mathématique" nach den damals vorhandenen Beobachtungsergebnissen die Strahiungsbilanz der Erde aufzustellen mich bemühte, ergaben sich aus denselben folgende numerische Werte der Grössen A, pa und pa′
| (38) | A = 0,40 pa = 0,80 pa′ = 0,06. |
Dies sind, wie man sieht, abgerundete Zahlen, weil damals ein höherer Grad der Genauigkeit nicht zu erreichen gewesen wäre. Trotzdem entsprachen diese Werte recht gut den Anforderungen meiner Berechnungen. Sie bildeten mit dem Kurlbaumschen numerischen Wert der Konstante σ des Stefanschen Gesetzes, von dem nachstehend noch, die Rede sein und Gebrauch gemacht werden wird, ein zusammenhängendes System von Konstanten, mit dem sich, wie nachfolgend gezeigt werden wird, aus dem der Tabelle VII zugrunde gelegten numerischen Wert der Solarkonstante eine mittlere Temperatur der untersten Luftschicht der Erdatmosphäre ergab, die nur um 0,l °C von der beobachteten abwich.
Dieses Ergebnis kann wie folgt gedeutet werden. Fasst man unsere Erde als ein Pyrheliometer auf, so sind die Grössen A, pa, pa′ und σ als Konstanten dieses riesigen Instrumentes zu betrachten. Die durch unzählige Beobachtungen ermittelte Temperatur der untersten Luftschicht der Erdatmosphäre stellt die an diesem Instrument zwecks Ermittlung der Intensität der Sonnenstrahlen abgelesene Temperatur dar. Aus dieser Temperatur ergab sich mit den erwähnten Instrumentkonstanten eine Solarkonstante von rund 2 Grammkalorien.
Weist dieses Instrument andere Konstanten A, pa, pa′ und σ auf, so müssen auch diese denselben richtigen Zusammenhang zwischen der Solarkonstante und der mittleren Temperatur an der Erdoberfläche ergeben. Benützt man also für A, pa, pa′die numerischen Werte (37), so muss, um den obigen richtigen Zusammenhang zu erhalten, der vierten Konstante σ ein entsprechender numerischer Wert zugewiesen werden, mit Rücksicht darauf, dass die Erde nicht als ein vollkommener Strahler zu betrachten ist, wie dies noch nachträglich erörtert werden wird.
Ich werde meinen Berechnungen des Temperaturfeldes der Erde das von mir in meiner "Théorie mathématique" und in der "Mathematischen Klimalehre" benützte System der Konstanten A, pa, pa′ und σ zugrunde legen, d. h. diese Berechnungen in ihrer ursprünglichen Form hier wiedergeben. Bei Benützung anderer numerischer Werte dieser Konstanten sind, ohne die Grundlagen der nachstehenden theoretischen Erörterungen anzutasten, keine abweichenden Hauptergebnisse der numerischen Ausrechnung zu erwarten.
Kapitel XVII
Zusammenhang zwischen Einstrahlung und Temperatur im Falle eines stationären Bestrahlungszustandes
§ 99. Differentialgleichungen der Strahlungsvorgänge in der Atmosphäre. Schwarzschild war wohl der erste, der die Strahlungsvorgänge in der Atmosphäre durch Differentialgleichungen mathematisch erfasst hat. Sie wurden im Jahre 1913 von Emden auf die Erdatmosphäre angewendet. Die Abhandlungen von Schwarzschild und Emden beziehen sich, wie aus ihren Titeln ersichtlich, auf das Strahlungsgleichgewicht, d. h. auf den stationären Strahlungszustand. Ich habe bereits im Jahre 1913 Untersuchungen über den variablen Bestrahlungszustand der Erde und der Planeten, wie er der Wirklichkeit entspricht, und den zugehörigen Temperaturzustand in Angriff genommen, diese Untersuchungen in meiner "Théorie mathématique" fortgesetzt und, soweit sie die Erde betrafen, in der "Mathematischen Klimalehre" zum Abschluss gebracht, wobei auch die Wärmeleitungsvorgänge im Erdboden mitberücksichtigt worden sind. Ich werde hier nach Ableitung der Differentialgleichungen für die variable Bestrahlung zuerst den einfacheren Fall des stationären Bestrahlungszustandes behandeln, um später auf den komplizierteren Fall der variablen Bestrahlung zu übergehen. Um die erwähnten Differentialgleichungen abzuleiten, müssen die im § 94 angeführten Annahmen gemacht werden. Es sollen ferner die durch Reflexionen an den Molekülen der Atmosphäre, an den Wolken und an der Erdoberfläche im Wärmehaushalt der Erde sich ergebenden Verluste der Sonnenstrahlung mathematisch derart ihre Berücksichtigung finden, dass man diese Verluste von der in die Atmosphäre eindringenden Sonnenstrahlung einfach in Abzug bringt, d. h. die an der oberen Grenze der Atmosphäre eindringende Sonnenstrahlung gleich
| (39) |

|
setzt, worin h die Höhe der Atmosphäre und A das bereits gekennzeichnete Reflexionsvermögen der Erde samt ihrer Atmosphäre bedeutet.
Im Wärmehaushalt der Erde muss neben der direkten auch die diffuse Sonnenstrahlung berücksichtigt werden. Es soll dabei angenommen werden, dass für diese beiden Strahlungen das Bouguer-Lambert′sche Gesetz gültig ist. Bezeichnet also J″(x) die Intensität der direkten und der diffusen Sonnenstrahlung in der Höhe x, so gilt analog der Gleichung (21) die Differentialgleichung:
| (40) |

|
wobei a1(x)dx das Absorptionsvermögen der zwischen den Höhen x und (x + dx) gelegenen Elementarschicht der Atmosphäre bei senkrechtem Durchgang der Strahlen bedeutet. Ueber die analytische Form der Funktion a1(x) wird später das notwendige gesagt werden.
Integriert man die Differentialgleichung (40) zwischen den Grenzen x = h und x = 0, so bekommt man:
| (41) |

|
als die Intensität der auf die Erdoberfläche auffallenden und von derselben absorbierten direkten und diffusen Sonnenstrahlung.
Die Grösse:
| (42) |

|
wird der Transmissionskoeffizient der Atmosphäre für die direkte und diffuse Sonnenstrahlung genannt. Es ist also:
| (43) |

|
d. h. wegen (39)
| (44) |

|
Diese Strahlung schliesst, weil die Refraktion nicht zu berücksichtigen ist, mit der Normalen der Erdoberfläche den Winkel z ein, der gleich ist der Zenitdistanz der Sonne und der für den diffusen Teil der Strahlung nur als ein Durchschnittswert zu betrachten ist.
Auf die Flächeneinheit des Erdbodens fällt während der Zeiteinheit die Strahlungsmenge:

|
Es stellt

|
jene Strahlung dar, die bei Abwesenheit der Atmosphäre den Erdboden treffen würde. Es ist also
| (45) |

|
Diese Strahlung wird, weil in A alle Reflexionen bereits inbegriffen sind, von der Erdoberfläche vollkommen absorbiert.
Auf die in der Höhe x befindliche horizontale Elementarschicht der Atmosphäre fällt während der Zeiteinheit eine Strahlungsmenge auf, die mit W(x, t) bezeichnet werden möge und die durch den Ausdruck
| (46) |

|
veranschaulicht ist.
Von dieser Strahlungsmenge wird von der Schicht der Betrag
| (47) |

|
d. h. wegen (40) der Betrag
| (48) |

|
absorbiert.
Es ist wegen (46) und (48)
| (49) |

|
Ausser der Strahlung W(x, t) durchsetzen die Atmosphäre dunkle Strahiungen, die von der Erdoberfläche gegen den Weitraum, d. h. von unten nach oben und solche, die von oben nach unten gerichtet sind. Zu diesen Strahlungen gehören die von der Erdoberfläche nach oben emittierte dunkle Strahlung und die von der Atmosphäre nach beiden Richtungen emittierten Strahlungen. Die von oben nach unten gerichtete Strahlung in der Höhe x und zur Zeit t soll mit O(x, t) und jene von unten nach oben gerichtete mit U(x, t) bezeichnet werden.
An der oberen Grenze der Atmosphäre, d. h. in der Höhe x = h, ist die Strahlung O(x, t) gleich Null, d. h. es ist
| (50) |

|
Zur Erdoberfläche gelangt von der Sonnenstrahlung der durch (45) dargestellte Betrag W(0, t), und von der dunklen Ausstrahlung der Atmosphäre der Betrag O(0, t), weiche beide Strahlungen, weil in A bereits alle Reflexionen inbegriffen sind, von der Erdoberfläche vollständig absorbiert werden.
Ausser den durch die Strahlungen W(0, t) und O(0, t) zugeführten Wärmemengen gelangt zur Erdoberfläche noch jene, die derselben durch Wärmeleitung oder Konduktion aus dem Boden zugeführt wird. Diese in der Zeiteinheit und pro Flächeneinheit der Erdoberfläche zugeführte Wärmemenge sei mit Qp bezeichnet. Alles in allem werden der Erdoberfläche während der Zeiteinheit die W6#228;rmemengen W(0, t), O(0, t) und Qp zugeführt und es wird sich auf derselben jene Temperatur einsteilen, bei weicher der Zufiuss der Wärme gleich dem Abfiuss ist, d. h. bei welcher die Emission der Erdoberfläche, die mit E bezeichnet werden möge, gleich der Summe der drei erwähnten Wärmemengen ist. Hieraus folgt:
| (51) |

|
Von der in der Höhe x befindlichen Elementarschicht der Atmosphäre wird während der Zeiteinheit der durch (49) dargestellte Betrag der Sonnenstrahlung absorbiert, und von den Strahlungen O(x, t) und U(x, t) die Beträge a1(x) O(x, t) dx und a2(x) U(x, t) dx, wobei a2(x) dx das Absorptionsvermögen der Elementarschicht für die dunklen Strahlungen bedeutet. Dieses Absorptionsvermögen ist, wie später auseinandergesetzt werden wird, verschieden von dem Absorptionsvermögen a1(x)dx der Schicht für die Sonnenstrahlung. Die Strahlungen, die die Eiementarschicht durch jede ihrer beiden Begrenzungsebenen emittiert, mögen mit ε(x, t) dx bezeichnet werden.
Aus dem vorstehenden folgt, dass in der Elementarschicht während der Zeiteinheit und pro Querschnittseinheit eine Wärmemenge aufgespeichert wird, die durch den Ausdruck:
| (52) |

|
veranschaulicht ist.
Diese Wärmemenge wird zur Erhöhung der Temperatur der Elementarschicht verwendet. Bezeichnet u(x, t) die in Celsiusgraden gemessene Temperatur der Elementarschicht zur Zeit t, so ist die pro Zeiteinheit stattgefundene Temperaturerhöhung durch (⊒u(x, t) ⁄ ⊒t veranschaulicht. Zwischen der zugeführten Wärmemenge dQ und der daraus sich ergebenden Temperaturerhöhung besteht die bekannte Relation:
| (53) |

|
worin ρ(x) die Dichte der Atmosphäre in der Höhe x und c, weil mechanische Arbeitsleistungen aus den vorliegenden Betrachtungen ausgeschlossen sein mögen, die spezifische Wärme der Atmosphäre pro Masseneinheit bei unverändertem Volumen bedeutet.
Es folgt aus (52) und (53)
| (54) |

|
Weitere zwei Differentialgleichungen werden auf folgende Weise erhalten. Beim Durchgang der von oben, also in der Richtung des abnehmenden x kommenden Strahlung O(x, t) durch die Elementarschicht wird diese Bestrahlung um den Betrag a2(x)O(x, t) dx geschwächt, d. h. in der Richtung +x um diesen Betrag verstärkt. Ausserdem wird diese Strahlung durch die Austrahiung der Schicht gegen die Erdoberfläche um den Betrag ε(x, t)dx verstärkt, d. h. in der Richtung +x um diesen Betrag geschwächt. Es ist also:
| (55) |

|
Beim Durchang der von unten kommenden Strahlung U(x, t) durch die Elementarschicht wird diese Strahlung um den Betrag a2(x)U(x, t)dx geschwächt und um den Betrag ε(x, t)dx verstärkt. Es ist also:
| (56) |

|
Im Falle eines stationären Strahlungs- und Temperaturzustandes, d. h. eines solchen, in dem die Grössen u, O, U und ε nur Funktionen von x, aber nicht von t sind, erhält man statt den vorstehenden partiellen Differentialgleichungen zwei gewöhnliche lineare Differentialgleichungen, die mit jenen von Schwarzschild abgeleiteten und von Emden, Baur und Philipps verwendeten identisch sind.
Den Gleichungen (55) und (56) kann man durch die Substitution:
| (57) |

|
eine für die späteren Anwendungen zweckmässigere Form geben. Die Addition bzw. die Subtraktion von (55) und (56) ergibt nämlich mit Berücksichtigung von (57)
| (58) |

|
|
| (59) |

|
Es folgt weiter aus (54), (49) und (57)
| (60) |

|
Die vorstehenden drei Gleichungen sind die drei Differentialgleichungen des Strahlungsvorganges in der Erdatmosphäre; dabei kann die Gleichung (59) durch die nachfolgende ersetzt werden, die aus (59) und (60) ohne weiters folgt,
| (61) |

|
Bei der Integration der vorstehenden partiellen Differentialgleichungen sind folgende Grenzbedingungen zu berücksichtigen.
Für x = 0, d. h. unmittelbar an der Erdoberfläche, ist die von unten kommende dunkle Strahlung der Atmosphäre gleich Null, so dass die mit U(0, t) bezeichnete Strahlung der Emmission E der Erdoberfläche gleich ist. Es ist also:
| (62) |

|
Setzt man dies in (57) ein, so wird:

|
d. h. wegen (51)
| (63) |

|
Es folgt aus (50) und (57)
| (64) |

|
§ 100. Integration der vorstehenden Differentialgleichungen für den Fall einer stationären Bestrahlung. Die Integration der vorstehenden Differentialgleichungen wird besonders einfach, wenn die Bestrahlung eine unveränderliche, d. h. der Bestrahlungszustand ein stationärer ist. Ein solcher FalI der Erdbestrahlung kommt, streng genommen, nie vor, weil wegen der Drehung der Erde und wegen ihres Umlaufes um die Sonne deren Bestrahlung fortwährenden Aenderungen unterworfen ist. Wenn es sich aber darum handelt, die mittlere Temperatur der Erde oder die mittleren jährlichen Temperaturen ihrer einzelnen Breiten zu berechnen, ist es gestattet anzunehmen, dass diese einer konstanten Bestrahlung ausgesetzt sind, die der mittleren jährlichen Bestrahlung gleich ist. Diese mittlere, an der oberen Grenze der Erdatmosphäre anlagende Bestrahlung sei mit Wm bezeichnet. Von derselben ist wegen den bereits besprochenen Reflexionen an den Luftteilchen, an den Wolken und an der Erdoberfläche nur der Betrag:
| (65) |

|
als für den Wärmehaushalt verwendbar zu betrachten. Von dieser Strahlung gelangt zur Erdoberfläche der durch den Transmissionskoeffizient
| (66) |

|
dargestellte Bruchteil, der das Verhältnis der tatsächlich durchgelassenen Strahlung (1 - A)Wm″ zur Strahlung (1 - A)Wm die in die Atmosphäre eindringt, veranschaulicht. Führt man diesen Transmissionskoeffizienten ein, dann kann z = 0 gesetzt werden.
Unter dem Einfluss der unveränderlichen Bestrahlung wird sich in der Atmosphäre ein stationärer Temperaturzustand ausbilden, weshalb zu setzen ist:
| (67) |

|
Es werden also in den vorstehend abgeleiteten Differentialgleichungen die Grössen u, X, Y, ε bloss Funktionen von x sein; dasselbe gilt auch von der Grösse W(x, t). Es folgt aus (49) mit z = O
| (68) |

|
d. h. nach Integration zwischen den Grenzen h und x und mit Berücksichtigung von (65)
| (69) |

|
Es ist also wegen (40)
| (70) |

|
Die Gleichungen (58), (61) und (60) erhalten wegen (67) die Form:
| (71) |

|
|
| (72) |

|
|
| (73) |

|
Hinsichtlich der Grenzbedingungen ist folgendes zu bemerken. Der jährliche Wärmefluss, der aus dem Erdinnern bis zur Erdoberfläche gelangt, ist, wie noch gezeigt werden wird, verschwindend klein im Vergleich zu den Wärmemengen, die die Sonnenstrahlung der Erdoberfläche zuführt. Es ist also Qp = 0 zu setzen und man bekommt statt (63) und (64)
| (74) |

|
|
| (75) |

|
Es folgt durch Integration von (72) mit Berücksichtigung von (74) und (70)
| (76) |

|
d. h. wegen (75) und (65)
| (77) |

|
Die Gleichungen (57), deren Subtraktion
| (78) |

|
liefert, ergeben mit Berücksichtigung von (77)
| (79) |

|
Dies besagt, dass die in die Atmosphäre eindringende Sonnenstrahlung (1-A)Wm als umgewandelte dunkle Strahlung U(h) dem Weltraum zurückgegeben wird.
Es folgt aus (71) und (76)

|
d.h. durch Integration zwischen den Grenzen h und x mit Berücksichtigung von (77)
| (80) |

|
Die Gleichungen (73) und (68) ergeben:
| (81) |

|
Es folgt aus (78)

|
d. h. wegen (80) und (74)

|
d. h. wegen (62)
| (82) |

|
Durch die vorstehenden Ergebnisse erscheinen die Differentialgleichungen (71), (72), (73) integriert, d. h. auf Quadraturen zurückgeführt. Um auch diese Quadraturen durchführen zu können und die Temperatur der Erdoberfläche und der einzelnen Schichten der Atmosphäre zu ermitteln, ist die Kenntnis des funktionalen Zusammenhanges zwischen x und a1(x) bzw. a2(x) und jenes zwischen der Emission E bzw. ε und der zugehörigen Temperatur erforderlich. Diesen funktionalen Zusammenhang vermitteln einige physikalische Gesetze, die jetzt herangezogen werden müssen.
§ 101. Gesetze von Beer, Kirchhoff und Stefan. Nach den Grundannahmen der Extinktionstheorie ist die Absorption des Sonnenlichts in der Atmosphäre um so grösser, je grösser die Anzahl der im Wege stehenden Luftpartikelchen ist, d. h. je dichter +s Medium ist. Wird diese Annahme auch hinsichtlich der gesamten Sonnenstrahlung und hinsichtlich der dunkten Ausstrahlung der Atmosphäre und der Erdoberfläche gemacht, so gelangt man zu den das sogenante Beersehe Gesetz zum Ausdruck bringenden Gleichungen:
| (83) |

|
worin k1 und k2 Konstanten sind, von denen k1 der Absorptionskoeffizient der Atmosphäre für die Sonnenstrahlung, k2, jener für die dunklen Strahlungen genannt wird; ρ(x) bedeutet die Dichte der Atmosphäre in der Höhe x.
Den Zusammenhang zwischen Einstrahlung und Temperatur vermitteln die sogenannten Strahlungsgesetze, von denen sich das Planck′sche Gesetz auf Strahlungen bestimmter Wellenlänge bezieht. Die Sonnenstrahlung als auch die dunklen Strahlungen der Erdoberfläche und der Atmosphäre sind aus den verschiedensten Wellenlängen züsammengesetzt. Wollte man auf alle diese Wellenlängen das Plancksche Gesetz anwenden, so müsste eine umfangreiche Arbeit geleistet werden, die kaum zu bewältigen wäre und sich für die Zwecke der hier niedergelegten Theorie nicht lohnen würde. Denn es handelt sich hier vornehmlich darum, einfache, genügend genaue, auch für das paläoklimale Problem verwendbare Formeln zu gewinnen. Aus diesem Grunde soll das kombinierte Strahlungsgesetz von Stefan und Kirchhoff zur Anwendung gelangen.
Nach dem Stefanschen Strahlungsgesetz emittiert ein vollkommen schwarzer Körper, der sich auf der absoluten Temperatur θ befindet, durch die Einheit seiner Oberfläche während der Zeiteinheit eine Strahlungsmenge, die durch den Ausdruck:

|
dargestellt ist, worin σ eine Konstante bedeutet.
Die bisherigen experimentellen Ermittlungen dieser Konstante lieferten etwas divergierende Resultate. Ich habe allen meinen Berechnungen den Wert:
| (84) |

|
gemmessen in Grammkalorien pro cm2 und Minute, zugrunde gelegt, der von Kurlbaum herrührt und auch von Emden benutzt wurde und der, obwohl um 7% kleiner als der zuletzt gefundene Wert dieser Konstante, sich durchhaus bewährt hat, wahrscheinlich deshalb, weil weder die Erdoberfläche noch die Erdatmosphäre als vollkommene Strahler zu betrachten sind.
Das Stefansche Gesetz gilt, wie bereits gesagt, nur für einen absolut schwarzen Körper, worunter ein solcher zu verstehen ist, dessen Absorptionsvermögen gleich eins ist. Ist dies nicht, der Fall, ist, also der in Betracht gezogene Körper ein sogenannter grauer, dessen Absorptionsvermögen kleiner als eins ist, so bedient man sich zur Berechnung der Emission eines solchen Körpers des Kirchhoffschen Strahlungsgesetzes.
Nach dem Strahlungsgesetz von Kirchhoff ist das Emissionsvermögen eines beliebigen Körpers für eine Strahlenart bestimmter Wellenlänge gleich seinem Absorptionsvermögen für diese Strahlenart multipliziert mit dem Emissionsvermögen des vollkommen schwarzen Körpers. Nimmt man an, dass dieses Gesetz auch für zusammengesetzte Strahlungen als gültig betrachten werden kann, was sich in der Folge als zulässig erweisen wird, so erscheint die Ausstrahlung des grauen Körpers durch den Ausdruck:

|
dargestellt, worin a das Absorptionsvermögen des Körpers für die emittierte Strahlungsart bedeutet.
Die Erdoberfläche und die Atmosphäre emittieren nur dunkle Strahlungen. Bezeichnet man das Absorptionsvermögen der Erdoberfläche für solche Strahlungen mit ap′ und jenes der in der Höhe x befindlichen Einheitsschicht, wie dies bereits geschehen ist, mit a2(x), so ergibt es sich, dass die Ausstrahlung. E der Erdoberfläche gleich ist:
| (85) |

|
worin θp die absolut gemessene Temperatur der Erdoberfläche bedeutet. Die Ausstrahlung ε(x) der in der Höhe befindlichen Einheitsschicht der Atmosphäre ist dagegen gleich:
| (86) |

|
worin θ(x) die absolut gemessene Temperatur dieser Schicht bedeutet.
Setzt man den Ausdruck (86) in die Gleichung (81) ein, so bekommt man
| (87) |

|
Setzt man den Ausdruck (85) in die Gleichung (82) ein, so wird
| (88) |

|
Dabei ist nach (40)
| (89) |

|
und nach (69)
| (90) |

|
§ 102. Das solare Temperaturfeld der Erde.
§ 103. Der Aufbau der Atmosphäre im Strahlungsgleichgewicht.
§ 104. Stabilitätsfragen.
§ 105. Einfluss des durchschnittlichen Wasserdampfgehaltes der Atmosphäre auf den thermischen Aufbau derselben. Neben ihren quantitativ fast unveränderlichen und qualitativ unwandelbaren Bestandteilen Stickstoff, Sauerstoff und Kohlensäure, enthält die Atmosphäre hauptsächlich noch Wasser in allen drei seinen Aggregatzuständen. Die Wandlungen und Uebergänge aus dem einen in einen anderen dieser Zustände bildet einen grossen Teil dessen, was man "Wetter" nennt. Eine aus ihren primären Ursachen abgeleitete mathematische Beschreibung dieser Naturerscheinung ist nach dem gegenwärtigen Stande der Wissenschaft nicht möglich, weshalb ich mich darauf beschränken muss, den Einfluss des durch die Gleichung (18) d.h. durch
| (158) |

|
veranschaulichten durchschnittlichen Gehaltes des Wasserdampfes auf den thermischen Aufbau der Atmosphäre mathematisch zu erfassen.
Schon Tyndall hat nachgewiesen, dass es nicht die Hauptbestandteile der Atmosphäre, nämlich die elementaren Gase Stickstoff und Sauerstoff, sind, welche die strahlende Energie nennenswert absorbieren, sondern dass diese Apsorption vorwiegend von gas- und dampfförmigen chemischen Verbindungen besorgt wird. Die Atmosphäre enthält von diesen Verbindungen, wie bereits gesagt, Wasserdampf und Kohlensäure, und diese Gase sind es, die den gr6#246;sseren Teil der Sonnenstrahlung und fast die gesamte Ausstrahlung der Erdoberfläche absorbieren.
Diesen Zustand will ich nun mathematisch zum Ausdruck bringen, wobei ich mir, um die Berechnung nicht allzusehr zu komplizieren, folgende Vereinfachungen erlaube. Weil der prozentuelle Gehalt der Atmosphäre an Kohlensäure, selbst in der untersten Luftschicht, geringer als 0,03 Prozent ist, will ich die trockene Luft samt der Kohlensäure als ein einheitliches Gas behandeln und nur dem Wasserdampf seine Sonderstellung einräumen. Die Dichteabnahme der Atmosphäre mit der Höhe ist dann nach dem soeben gesagten durch die Formel
| (159) |

|
dargestellt, worin ρ1 und ρ2 die Dichte der trockenen Luft bzw. des Wasserdampfes unmittelbar oberhalb der Erdoberfläche bedeuten soll. Für H ist der bereits erprobte Wert H = 8.000 m zu setzen. Eine weitere Vereinfachung, die ich mir noch erlaube, besteht darin, dass ich die Absorption der Sonnenstrahlung gänzlich der trockenen Luft und der Kohlensäure überweise. Ich setze also mit Anwendung des Beersehen Gesetzes:
| (160) |

|
worin a1 das Absorptionsvermögen der untersten Einheitsschicht der trockenen Luft samt Kohlensäure für die Sonnenstrahlung, a1′ jenes für die dunkle Ausstrahlung der Erdoberfläche bedeutet, während a2′ das Absorptionsvermögen der untersten Einheitsschicht des in der Atmosphäre enthaltenen Wasserdampfes für die erwähnte dunkle Strahlung darstellet.
Die Transmissionskoeffizienten pa und pa′ der derart aufgebauten Atmosphäre für die Sonnenstrahlung bzw. für die dunkle Strahlung sind nach (42) durch die folgenden Ausdrücke veranschaulicht:
| (161) |

|
Es ist deshalb nach (95)
| (162) |

|
und nach (87)
| (163) |

|
Mit Anwendung der Substitution

|
und mittels partieller Integration bekommt man:

|
so dass man nach demselben Vorgang wie in § 102 erhält:
| (164) |

|
Diese Gleichung liefert ein bemerkenswertes Resultat, nämlich, dass die Lufttemperatur schon in einer endlichen Höhe ihr Minimum erreicht. Differetitiert man, um dies zu erweisen, die vorstehende Gleichung nach x und setzt das Resultat gleich Null, so bekommt man:
| (165) |

|
Dabei ist mit e-x⁄H gekürzt worden, was zu besagen hat, dass auch für x = ∞ die Temperatur ein Extrem, ein Nebenminimum, erreicht.
Berücksichtigt man, dass wegen (160) ln pa = -a1 · H ist, setzt der kürzeren Schreibweise halber
| (166) |

|
so bekommt man statt (165) die Gleichung:
| (167) |

|
Aus dieser Gleichung lässt sich jenen Höhe x berechnen, in der die Lufttemperatur ihr absolutes Minimum erreicht.
Zu einer solchen Berechnung braucht man ausser dem bereits angegebenen numerischen Werte von H noch jenen der Grössen a1, a1′ und a2′. Es folgt aus (38) und der Tabelle XV pa = 0,67; pa′ = 0,05 d.h.
| (168) |

|
Dieser letztere Ausdruck stellt die durch die Luft und den Wasserdampf bewirkte Transmission der Erdausstrahlung dar. Wie gross der Anteil jedes dieser beiden Gase an dieser Transmission ist, darüber gibt uns eine diesbezügliche Untersuchung Ekho1m′s wenigstens annähernd Auskunft. Darnach soll die trockene Luft samt der Kohlensäure rund 25 Prozent, der Wasserdampf dagegen 60 Prozent absorbieren, woraus folgen würde:

|
d. h.
| (169) | a2′ = 10 a1′ |
Aus (168) und (169) folgt: a1 = 0,0501; a1′ = 0,0864; a2′ = 0,8642, und die Gleichung (167) bekommt folgende numerische Form:
| (170) | (0,0864 + 0,8642 · z2)3 - 0,0025 · (0,0864 + 0,8642 · z3) - 0,0108 · z = 0. |
Aus der vorstehenden Gleichung folgt: z = 0,268, d. h. x = 10.539 m.
Dies besagt, dass in der Höhe von 10,5 km die jährliche Mitteltemperatur der Luft ihr Minimum erreicht. Diese Erscheinung, die durch einige Nebeneinflüsse, von denen noch die Rede sein wird, beeinflusst wird, führt den Namen der oberen Temperaturinversion.
Den Einfluss, den der Wasserdampf bzw. die Kohlensäure auf die Absorption der Erdausstrahlung ausüben, haben L. de Marchi bzw. Arrhenius zur Grundlage ihrer Eiszeitentheorien gemacht. Ich habe diese beiden Theorien im § 60 meiner "Théorie mathématique" besprochen und die Gründe ihrer Unzulänglichkeit klargelegt.
Kapitel XVIII
Zusammenhang zwischen Einstrahlung und Temperatur im Falle einer variablen Bestrahlung
§ 106. Die Wärmeleitung des Erdbodens.
§ 107. Der Wärmeumsatz des Erdbodens.
§ 108. Integration der Differentialgleichungen des Strahlungsvorganges in der Atmosphäre im Falle variabler Bestrahlung.
§ 109. Vertikale Fortpflanzung der Temperaturoszillationen in der Atmosphäre.
§ 110. Der jährliche Wärmeumsatz der Atmosphäre.
Sechster Abschnitt
Das Eiszeitalter: sein Mechanismus, seine Gliederung und Chronologie
Kapitel XIX
Das Eiszeitenproblem und seine Geschichte
§ 111. Die Eiszeiten. Den beschreibenden Naturwissenschaften ist es in hundertjähriger forschender Arbeit gelungen nachzuweisen, dass während der jüngsten geologischen Periode, dem Quartär, ein Zeitalter grosser klimatischer Umwälzungen über die nördlichen Gegenden der Erde herangebrochen war, die in den sogenannten Eiszeiten ihren mächtigsten Ausdruck fanden und diesem Zeitabschnitt der Erdgeschichte den Namen des Eiszeitalters gaben. Eine fast unübersehbare Menge von Tatsachenmaterial wurde zutage gefördert, das dieses Naturereignis beglaubigte. Davon soll hier zum besseren Verständnis des nachfolgenden nur das wichtigste mitgeteilt werden, wobei ich den Ausführungen des im Jahre 1924 erschienenen Buches von Köppen und Wegener "Die Klimate der geologischen Vorzeit" folge, dessen letztes Kapitel die Klimate des Quartärs behandelt, welches von Köppen verfasst wurde. Dieses Kapitel beginnt mit einer Uebersicht der Tatsachen, worin die für das Klimaproblem in Betracht zu ziehenden Ergebnisse der erdgeschichtlichen Forschung übersichtlich zusammengestellt sind. Diese Ausführungen Köppens kennzeichnen treffend den damaligen Stand der Eiszeitenfrage und so wird man an der Hand dieses Berichtes das seither geleistete gut überblicken können.
Nachdem Europa und Nordamerika seit der algonkisch-kambrischen Vereisung während ungeheuer langer Zeiträume tropisches bis subtropisches Klima gehabt haben, begann für sie gegen Ende der Tertiärzeit ein neues Zeitalter, zuerst in Nordamerika, dann auch in Europa, das seinen Höhepunkt im Quartär erreichte. In den Gebirgen senkte sich die Schneegrenze wiederholt um etwa 1.200 Meter, so dass in den einzelnen Eiszeiten weite Teile beider Festländer unter einem kilometermächtigen Inlandeise begraben lagen, während in den Intergrazialzeiten das Eis ganz oder teilweise wegschmolz und ein Flora ähnlich der heutigen in das freigegebene Land einzog.
Schon im Anfange des neunzehnten Jahrhunderts haben Playfair und Schimper, später Venetz, Charpetier und viele andere erkannt, dass sich in den Alpen diese Vereisungserscheinungen nur durch die Annahme einer einst viel grösseren Ausdehnung der Gletscher erklären lassen. Das Netz von Eisströmen, das die Alpen durchzog, überfloss viele der Pässe, und im Norden breiteten sich am Fuss des Gebirges die aus den Tälern herausgeflossenen Eismassen zu ausgedehnten Vorlandgletschern aus.
A. Penck und E. Brückner haben die Spuren dieser quartären Vereisung in den Alpen eingehend untersucht und ihr umfangreiches Beobachtungsmaterial in dem dreibändigen Werk "Die Alpen im Eiszeitalter" niedergelegt. Hauptsächlich auf Grund der Schotterterrassen der Flüsse kamen sie zu dem Ergebnis, dass die Vereisung viermalig war, mit drei dazwischenliegenden Interglazialzeiten. Sie bezeichneten diese Eiszeiten als Günz-, Mindel-, Riss- und Wurm-Eiszeit. Von den Interglazialzeiten muss diejenige zwischen der Mindel- und Riss-Eiszeit weitaus die längste gewesen sein.
Ueber die absolute Zeitdauer dieser einzelnen Phasen des Eiszeitalters hat Penck im Schlussband des erwähnten Werkes interessante und, wie es sich später erweisen sollte, gut zutreffende Schätzungen mitgeteilt, die er hauptsächlich aus der festgestellten Erosion der in den Eiszeiten abgelagerten Flussschotter erhalten hatte und die er durch ein Graphikon veranschaulichte, das in der beiliegenden Fig. 47 wiedergegeben ist.

Nach diesem Graphikon schätzt Penck die Zeitdauer seit der Ablagerung der Bühl-Moränen im Vierwaldstätter See auf rund 20.000 Jahre und wählt diese Zeitspanne als Einheit, so dass die Riss-Würm-Interglazialzeit mit 60.000 Jahren, die vorhergehende, die Mindel-Riss-Interglazialzejt, viermal länger, also mit 240.000 Jahren zu veranschlagen wären. Ueber die Dauer der Eiszeiten selbst spricht Penck keine Vermutung aus; nach seinem Graphikon wäre die seit Beginn der Günz-Eiszeit verflossene Zeitdauer mit etwa 660.000 Jahren zu bewerten.
Die in den Alpen gewonnenen Anschauungen boten schon frühzeitig Anlass, die quartäre Ueberschüttung Nordeuropas bis zum südlichen England, dem Harz und den Karpaten mit ungeheuren Massen von Tonen, Kiesen und Findlingsblöcken nicht mehr den noch zu erwähnenden Fluten oder schwimmenden Eisschollen, sondern der Wirkung des Eises zuzuschreiben, indem bewiesen wurde, dass die Verfrachtung dieser Massen nur durch Gletscher, nämlich durch ein ganz Nordeuropa bedeckendes Inlandeis erfolgt sein müsse. Aber trotz allen Bemühungen war es der Wissenschaft in ihrem Stadium, auf das sich die Köppensche Darstellung bezieht, nicht gelungen restlose Klarheit in die Gliederung des norddeutschen Quartärs und ihre Beziehung zur Gliederung der alpinen Eiszeiten zu bringen und das Penck-Brückner sehe Schema auch hier anzuwenden. Hier hatten nämlich die Forschungen von Gagel, Soergel, Krenke1 und anderer ergeben, dass die letzte, die Würmeiszeit, in drei Hauptstösse zergliedert werden muss, die man mit den Namen Wü:rm I, Würm II und Würm III bezeichnete. Aehnliches galt auch für England, wo man mehrere Eiszeiten, sechs, festgestellt hatte.
In Skandinavien, nahe dem Herd der Vergletscherung, ist die Gliederung in Eis- und Interglazialzeiten sehr verwischt, da diese Länder Ausräumungsgebiet waren. Dennoch sind dort Funde gemacht, die wenigstens für die Existenz einer eisfreien Interglazialzeit sprechen. Das Inlandeis muss also wenigstens in einer der Interglazialzeiten auch in Skandinavien so gut wie ganz verschwunden gewesen sein. Auch für die Halbinsel Kola und die Küste des Weissen Meeres wurde eine Interglazialzeit festgestellt. Vermutlich handelt es sich hier wie auch in Skandinavien um die lange Mindel-Riss-Interglazialzeit, in der die Bedingungen für eine völlige Beseitigung des Inlandeises am günstigsten waren.
Auch in dem nicht von Eis bedeckten Gebiet Europas bildeten sich im Quartär Ablagerungen, die von unmittelbarem klimatischem Interesse sind und welche bezeugen, dass die Zahl der Klimaschwankungen viel grösser war als in dem einfachen Penck-Brücknerschen Schema. Aehnliches bezeugen auch die geologischen Belege, die uns über periodische Klimaänderungen in den aussereuropäischen Ländern Kunde geben.
Obwohl es auf diese Weise den beschreibenden Naturwissenschaften gelungen war, Aufschluss über die Ausdehnung und den ungefähren Verlauf der Vereisungen Europas und Nordamerikas zu erlangen, war es ihnen versagt, etwas üüber die Ursachen dieser Naturerscheinung auszusagen. Diese Ursachen lagen ausserhalb des Gesichtsfeldes dieser Wissenschaften. Sie werden den Gegenstand meiner nachfolgenden Ausführungen bilden. Zuvor möchte ich des geschichtlichen Interesses wegen über einige misslungene Versuche, das Eiszeitenproblem zu lösen, berichten, um dadurch eine scharfe Grenze zwischen diesen Versuchen und meinen Untersuchungen zu ziehen, da man diese letzteren oft irrtümlicher Weise mit jenen ersteren zu verwechseln pflegte.
Ueber die Eiszeitentheorien von L. de Marchi und Arrhenius habe ich im § 105 dieses Buches kurz, in meiner "Théorie mathématique" ausführlicher berichtet. Hier will ich die geschichtlich interessantesten der Theorien kurz besprechen, die das Eiszeitenphänomen durch astronomische Ursachen zu erklären bemüht waren und deshalb unter dem Namen der astronomischen Theorien der Eiszeiten bekannt sind.
§ 112. Die alten Theorien der Eiszeiten. Meines Wissens nach war es Adhémar der erste, der die grossen klimatischen Umwälzungen des Quartärs durch astronomische Ursachen zu erklären versuchte. In seinem Werke "Les réolutions de la mer, déluges periodiques. Paris 1842 und (zweite Auflage) 1860" trat er vor die gelehrte Welt mit diesem damals gerade aktuell gewordenen Problem, denn kurz vorher hatte man den nordischen Ursprung der über einen grossen Teil von Europa zerstreuter Steinschuttmassen und Blöcke erkannt und man suchte nach Erklärungen, wie diese Massen südwärts verfrachtet worden sind.
Mehrere diesbezügliche Hypothesen stritten damals um Anerkennung. Nach der einen derselben waren es schwimmende Eisschollen, nach der anderen, vom Pole sich ergiessende Fluten, nach der dritten, südwärts sich drängende Gletscher, die jene Verfrachtung besorgten. Adhémar, noch im Banne der Cuvier′schen Ideen stehend, nach denen unser Planet durch eine Reihe gewaltsamer revolutionärer Umgestaltungen wiederholt verheert und jedesmal durch einen neuen Schöpfungsakt von einer neuen Organismenwelt besiedelt wurde, suchte vor allem die Hypothese katastrophaler Fluten durch seine Theorie zu stützen, deren Leitgedanke der folgende ist.
Wegen der Präzession der Nachtgleichen und der Bewegung des Perihels und der daraus sich ergebenden Veränderlichkeit der Dauer der Jahreszeiten, werden, wie im vierten Abschnitt dieses Buches auseinandergesetzt, alle zehn Jahrtausende auf jeder der beiden Hemisphären kurze und milde Winter mit langen und strengen abwechseln und zwar so, dass wenn eine der Hemisphären einen sehr strengen Winter hat, die andere eines milden sich erfreut. Auf der ersteren häufen sich wegen zunehmender Kälte um den zugehörigen Pol die Eismassen derart an, dass die dadurch vermehrte Massenanziehung eine Ueberflutung dieser Halbkugel verursacht, die von einer weiteren Abkühlung begleitet ist. Die südliche Halbkugel, die gegenwärtig den längeren Winter hat, veranschaulicht mit ihrer grossen Eiskalotte und überwiegender Wasserbedeckung nach Adhémars Meinung diesen Sachverhalt. Die um den Pol angehäuften Eis- und Wassermassen werden mit dem Eintritt der Periode wärmerer Winter abzufliessen beginnen, Gesteinsmassen polarer Gegenden mitführend. Stürzt nachher die morsch gewordene, auf dem Pole pilzhutartig aufsitzende Eiskappe plötzlich ein, so ergiessen sich vor ihr aus katastophale Fluten über die Erde. Solche Katastrophen wiederholen sich, abwechselnd auf beiden Hemisphären, alle zehn Jahrtausende.
Spätere geologische Untersuchungen haben die Frage klimatischer Veränderungen auf der Erde klarer beleuchtet, indem vor allem festgestellt wurde, dass während gewisser Zeitintervalle des Diluviums grosse Gebiete von Europa und Nordamerika unier einer mächtigen Eisdecke begraben lagen und die erwähnten Steinmassentransporte nur durch Gletscher bzw. Inlandeis geschehen konnten. Die Drifthypothese der schwimmenden Eisschollen und jene der katastrophalen Fluten wurden gänzlich verworfen. Die Adhémar′sche Theorie konnte sich, auch in ihrer für das Gletscherphänomen zurechtgelegten Form, nicht mehr halten, nachdem bewiesen wurde, dass die Eisanhäufungen der diluvialen Eiszeit bei weitem nicht von jener Grösse waren, um die von dieser Theorie angenommene Ueberflutung der vereisten Hemisphäre herbeizuführen. Nichtsdestoweniger wurde die Theorie von Adhémar zum Ausgangspunkt anderer Theorien der Eiszeiten, von denen die bemerkenswerteste jene von Croll ist.
Die Theorie von Croll, die er in seinen Werken "Climate and time in their geological relations, a theory of secular changes of the earth′s climate. London 1875. -- Discussions on climate and cosmology. London 1889" niedergelegt hat, knüpfte, wie jene von Adhémar, an die ungleiche Dauer der Jahreszeiten an, weist aber gegenüber dieser letzteren schon in diesem Punkte eine Fortschritt auf, weil Croll den Einfluss der Exzentrizität der Erdbahn auf die Dauer der astronomischen Jahreszeiten richtig erkannt hat. Nur bei einer relativ grossen Exzentrizität der Erdbahn kann der Unterschied zwischen Sommer- und Winterhalbjahr beträchtlich werden. Trifft es sich also zu, dass bei einer bemerkenswerten Exzentrizität die Aequinoktiallinie sich der Normalen der Apsidenlinie nähert, so wird jene Hemisphäre der Erde, deren Winter mit dem Durchgang der Erde durch das Aphelium zusammenfällt, einen langen und strengen Winter haben. Dann wird in ihrer gemässigten Zone Schnee auch in jenen Breiten fallen, wo jetzt nur Regen fällt, und wenn auch der Schneefall nicht besonders gross ist, wird die Schneedecke doch bleiben und nicht schmelzen, weil die Temperatur tief unter dem Gefrierpunkt bleibt. Wenn dann der Frühling und Sommer herannahen, wird die steigende Temperatur durch die grössere Verdunstung auf den Meeren zuerst den Schneefall auf dem Lande steigern. Wenn aber später der Schnee auch zu schmelzen beginnt, wird es doch lange dauern, bis das niedrige Land schneefrei wird, und auch auf nicht sehr hohen Bergen wird der Schnee liegen bleiben, und bald im Herbste beginnt der Schneefall von neuem. Das nächste Jahr bringt eine Wiederholung dieses Vorganges mit dem Unterschiede, dass nun die Schneelinie zu einem niedrigeren Niveau herabsteigt als im Vorjahr. Jahr auf Jahr wird so die Schneegrenze herabsteigen, bis endlich alles höhere Land dauernd mit Schnee bedeckt bleibt. Die Täler füllen sich dann mit Gletschern und ein grosser Teil dieser Hemisphäre wird mit Eis und Schnee bedeckt bleiben. Damit kommt ein neuer mächtiger Faktor zur Geltung: die Wirkung der Schneedecke, die auch während des Sommers die Luft abkühlen, dichte anhaltende Nebel erzeugen wird, die die Sonenstrahlen abhalten und das Schmelzen des Schnees stark verzögern werden.
Während sich derart Schnee und Eis auf der einen Hemisphäre anhäufen, vermindern sie sich auf der anderen. Dies verstärkt die Passatwinde auf der kalten Hemisphäre und schwächt sie auf der wärmeren. Die Wirkung wird sein, dass das warme Wasser der Tropenmeere mehr und mehr in die mittleren Breiten der warmen Hemisphäre hinübertreiben wird. Diese Ablenkung der Wärmequellen von der kalten Hemisphäre wird wieder die Anhäufung von Schnee und Eis auf derselben begünstigen, und damit werden die warmen Strömungen noch weiter abgeschwächt, So verstärken sich diese beiden Wirkungen gegenseitig.
Der gleiche Prozess einer gegenseitigen Aktion und Reaktion tritt auch auf der warmen Hemisphäre zutage, nur in gerade entgegengesetzter Richtung, In dieser wirkt alles zusammen, die mittlere Temperatur zu erhöhen und die Menge von Schnee uud Eis zu verringern. Diese Hemisphäre befindet sich also in einer Interglazialzeit.
Mit der Aenderung der Länge des Perihels zum jeweiligen Frühlingspunkt ändern sich die obigen Verhältnisse. Ist die Aequinoktiallinie zur Koinzidenz mit der Apsidenlinie gekomm:n, dann sind die beiden Hemisphären hinsichtlich der Bestrahlung gleichgestellt und befinden sich in einer Uebergangszeit, aus der die früher vereiste Hemisphäre in eine Interglazialzeit, die andere in die Eiszeit gelangt. So reihen sich auf jeder der beiden Hemisphären Eis-, Uebergangs- und Interglazialzeit aneinander und zwar immer so, dass wenn eine Hemisphäre die Eiszeit hat, die andere die Interglazialzeit durchlebt. Die geschilderten Wirkungen werden mit zunehmender Exzentrizität der Erdbahn verstärkt, mit abnehmender geschw6#228;cht.
Gegen die hier nur in ihren Hauptzügen wiedergegebene Theorie von Croll hat mannigfaltige Einwände erhoben. Von klimatologischer Seite, als den schwerwiegendsten, den Einwand, dass die Gletscher nicht durch einen strengen Winter begünstigt werden, sondern dass in Gegenteil ein solcher der Bildung grosser Gletscher hindernd entgegenwirkt, wie man dies in den Gebieten strenger Winterkälte im Innern der nördlichen Kontinente, namentlich in Sibirien, beobachten kann. Nicht ein strenger Winter, sondern ein kühler Sommer begünstigt das tiefe Herabsteigen der Gletscherströme.
Die Einwände, die man von geologischer Seite gegen die Crollsche Theorie erhoben hat, gipfeln in folgendem. Nach Croll würden die Eiszeiten auf jeder Hemisphäre alle zwanzig Tausend Jahre, allerdings in wechselnder Stärke, wiederkehren. Dem widerspricht die geologische Erfahrung, die zwar eine Reihe von Eiszeiten zugibt, jedoch nicht in so kurzen und regelmässigen Intervallen. Im Gegensatz zur geologischen Erfahrung würden nach Croll die Eiszeiten auf der nördlichen und der südlichen Hemisphäre abwechselnd in Erscheinuug treten; eine gleichzeitige Vereisung beider Hemisphären wäre ausgeschlossen.
Ich habe mich in meiner "Théorie mathématique" etwas ausführlicher mit der Theorie von Croll befasst und ihre Unzulänglickheit in dem Umstand aufgedeckt, dass in derselben der Einfluss der Veränderlichkeit der Ekliptikschiefe auf die Bestrahlung der Erde nur ungenügend berücksichtigt war. Daran krankten und scheiterten die nachher unternomtnenen Versuche, die Eiszeiten rechnerisch zu erklären, wie dies nachstellend gezeigt werden soll.
§ 113. Ueber einige weiteren Versuche, die Eiszeiten rechnerisch zu erklären. R. Ball hat in seinem Werke "Astronomical theory of the glacial period. The Cause of an Ice Age, London 1891" die Theorie von Croll wieder aufgenommen und ihr eine neue mathematische Fassung zu geben versucht, die jedoch keinen Fortschritt bedeutet. Ba11 berücksichtigte zwar den Einfluss der Aenderungen der Ekliptikschiefe auf den Bestrahlungszustand der Erde, aber nur in bezug auf die sommerliche bzw. winterliche Bestrahlung der ganzen in Betrach gezogenen Hemisphäre. Diese Bestrahlungen sind durch die Formeln (108) des vierten Abschnittes dieses Buches veranschaulicht. Aus diesen Formeln folgt, dass bei einem Zuwachs der Ekliptikschiefe von einem Bogengrad diese Bestrahlungen folgende prozentuellen Aenderungen erleiden:

|
Setzt man in diese Ausdrücke den gegenwärtigen numerischen Wert der Ekliptikschiefe ein, so findet man, dass diese Aenderungen +0,81 bzw. -1,37 Prozent betragen. Diese Beträge sind in Verhältnis zu den in der Tabelle XI11 mitgeteilten auf die höMheren Breiten sich beziehenden Aenderungen recht klein. Wie man sieht, haben die Aenderungen der Ekliptikschiefe keinen stärkeren Einfluss auf die totalen Bestrahlungen der einzelnen Hemisphären, sondern machen sich erst in der Verteilung der Sonnenstrahlung innerhalb dieser Hemisphären besonders fühlbar. Bei der Betrachtungsweise von Ball bleibt diese ausschlaggebende Wirkung der Aenderungen der Ekliptikschiefe gänzlich unbeachtet.
Dieselbe Unzulänglichkeit weist der von Pilgrim in seiner im § 84 angeführten Arbeit und in der nach seinem Tode von W. Wundt herausgegebenen Abhandlung "Die Berechnung der Eiszeiten auf astronomisch-physikalischer Grundlage. Jahreshefte des Vereins für vaterländische Naturkunde in Württemberg. 84. Jahrg. 1928" unternommene Versuch, die Eiszeiten rechnerisch zu behandeln. Trotzdem stellt die Arbeit dieses Forschers einen wesentlichen Fortschritt in der Behandlung des Eiszeitenproblems dar, weil, wie im § 84 ausgeführt, er der erste war, der die säkularen Aenderungen der auf den Bestrahlungszustand der Erde Einfluss habenden Elemente sachgemäss berechnete, so dass seine diesbezüglichen Rechnungen der weiteren Erforschung der Eiszeitenfrage dienstbar gemacht werden konnten.
Auch Hargreaves hat zur Erforschung des Eiszeitenproblems positives geliefert. In seiner im § 72 bereits angeführten mathematisch einwandfreien Arbeit hat er den Aenderungen der Ekliptikschiefe mehr Aufmerksamkeit geschenkt als alle früheren Forscher, doch hat er dabei nur die Auswirkung dieser Aenderungen auf die ganzjährigen Bestrahlungen der einzelnen geographischen Breiten in den Bereich seiner Untersuchungen einbezogen. Diese Aenderungen sind, wie aus der Tabelle XI11 ersichtlich, recht klein im Vergleich zu jenen der halbjährigen Strahlungsmengen, so dass in den Berechnungsergebnissen von Hargreaves die für die Entstehung der Vereisungen ausschlaggebende periodische Verschärfung und Abschwächung der jahreszeitlichen Gegensätze gar nicht zum Vorschein gelangt.
In neuerer Zeit hat sich R. Spitaler viel mit dem Eiszeitenproblem beschäftigt und die Ergebnisse seiner Arbeit in zwei besonderen Monographien zusammengefasst. Die erste derselben erschien im Jahre 1921 unter dem Titel "Das Klima des Eiszeitalters". Der rechnerische Aufbau dieser umfangreichen Arbeit beruht auf der Anwendung der im vierten Abschnitt des vorliegenden Buches angeführten Formel (1O), die, wie dort auseinandergesetzt, unrichtig ist. Wie weit diese Formel von den tatsächlichen Bestrahlungsverhältnissen abweicht, ist aus der hier mitgeteilten mit Hilfe der Rechnungsergebnisse von Wiener konstruierten Fig. 37 und aus der zugehörigen Tabelle V ersichtlich. Die meridionalen Schnitte der durch die Fig. 37 dargestellten Fläche stellen die meridionale Verteilung der der Erde im Laufe des Jahres zugestrahlten Wärmemengen dar. Diese Schnitte sind mit Ausnahme der Kurven AED, KLM und ARC keine einfachen Kosinuslinien, wie es die von Spita1er benützte Formel verlangt, vielmehr weit davon entfernt, solche Linien zu sein. Man betrachte beispielsweise die Linie HGF, die in der mit Benützung der Rechnungsergebnisse von Angot entworfenen Fig. 44 durch die oberste, dem Transmissionskoeffizient p = 1 entsprechende Kurve ebenfalls veranschaulicht ist. Die Bestrahlungsverhältniss+ der Erde sind also viel komplizierter als es Spita1er irrtümlicherweise annahm und sie durch einfache Formeln, für die er eingestandenermassen eine besondere Vorliebe hatte, darzustellen glaubte, weshalb alle seine aus dieser Formel gewonnenen Rechnungsergebnisse unrichtig sind und im krassen Widerspruch stehen mit jenen der soeben genannten Forschern und auch aller übrigen, die sich mit derselben Frage befassten.
Es ist auf Grund der obigen Feststellung vollständig überflüssig, auf die anderen rechnerischen Fehler, die in den soeben angeführten Arbeit von Spita1er vorkommen, näher einzugehen; es sei nur beispielweise erwähnt, dass Spita1er die Perihellänge zu Beginn des Jahres 1850 mit 280° 21′ 42″ in seine Rechnung stellt, während sie in Wirklichkeit, wie aus der mitgeteilten Tabelle VIII von Stockwell-Pilgrim ersichtlich gleich 100° 24′ gewesen ist.
Dreissig Jahre lang hat Spitaler an der Richtigkeit seiner Berechnungen zähe festgehalten, die von ihm berechneten Bestrahlungen der Erde als die wahren bezeichnet und alle von den seinigen abweichenden Rechnungsergebnisse für falsch erklärt, um schliesslich in seiner Arbeit "Die Bestrahlung der Erde durch die Sonne und die Temperaturverhältnisse der quartären Eiszeit. Prag 1940" seine früheren Berechnungen als "gegenstandslos" zu erklären. In dieser seinen neuesten Arbeit versucht er auf einem anderen Wege, ebenfalls mit Benützung einer "einfachen" Formel, der Lösung des Problems beizukommen. Er tat dies auf folgende Weise.
Um die mittlere tägliche Bestrahlung eines Punktes der Erdoberfläche zu erhalten, zieht Spita1er den Bestrahlungsmeniskus eines Breitekreises, wie er etwa durch die in der Fig. 36, Seite 291, gestrichelte Fläche, dargestellt ist, in Betracht und bezeichnet die durch diesen Meniskus während eines Tages zugestrahlte Wärmemenge mit S. Dann glaubt Spita1er die mittlere tägliche Bestrahlung eines Punktes dieses Breitekreises durch folgende Ueberlegungen, die ich seiner Abhandlung wörtlich entnehme, gewinnen zu können.
"Diesen Bestrahlungsmeniskus kann man sich der Sonne gegenüber als festliegend denken. Nun rotiert die Erde während eines Tages an dem Bestrahlungsmeniskus vorüber, und ein Punkt nach dem anderen kommt in seinen Bereich und erhält während seines Vorüberganges von Sonnenaufgang bis Sonnenuntergang dieBestrahlungssumme S. Man erhält daher die mittlere tägliche Bestrahlung eines Punktes. wenn man die Summe S durch die Grundlinie des Bestrahlungsmeniskus, d. h. durch die Länge des vom Meniskus überspannten Bogens B dividiert... Wiener und Mi1ankovitch dividieren die Summe S aber immer durch den ganzen Kreisumfang, durch 2π.
Die vorstehenden Ueberlegungen Spitalers sind unrichtig, wie ich dies auch an anderer Stelle ausführlich auseinandergesetzt habe. Um dies ersehen, ziehe man, weil man von der Bestrahlungsmenge einer Linie, so wie es Spitaler tut, eigentlich nicht reden kann, einen längs des Breitekreises um die Erde geschlungenen schmalen Ring in Betracht, dessen Breite 1 cm beträgt. Bezeichnet man, so wie ich es im vierten Abschnitt diese Buches getan habe, die an einem beliebigen Punkte dieses Ringes der Flächeneinheit pro Zeiteinheit zugeführte Wärmemenge mit dW ⁄ dt, mit ψ1 die geographische Länge dieses Punktes, gezählt, wie in der Fig. 36 angegebenen, und mit r den Radius des in Betracht gezogenen Breitekreises, so ist die durch den Bestrahlungsmeniskus dem Breienkreisring während der Zeiteinheit zugeführte Strahlung durch das Integral

|
veranschaulicht, wobei sich dieses Integral über den bestrahlten Teil des Breitekreises zu erstrecken hat. Die Integrationsgrenzen -ψ0. und +ψ0 ergeben sich durch Auflösung der Gleichung

|
d. h der Gleichung (20) des erwähnten Abschnittes.
Während eines mittleren Sonnentages, dessen Länge, die mit τ bezeichnet werden möge, 1.440 Minuten beträgt, wird dem in Betracht gezogenen Ring die von Spita1er mit S bezeichnete Strahlungsmenge zugeführt, die also durch

|
veranschaulicht ist.
Weil die Erde im Laufe eines Sonnentages eine vollständige Drehung in bezug auf die Sonne vollführt, gleitet der erwähnte Ring unter dem Bestrahlungsmeniskus, den man, wie oben gesagt, der Sonne gegenüber als festliegend zu denken hat, derart, dass im Laufe eines Tages alle seine Elemente der Bestrahlung durch die Sonne in gleichem Masse teilhaftig werden. Die tägliche Bestrahlung W, der Flächeneinheit dieses Ringes wird also erhalten, wenn man die Strahlungsmenge S durch die Oberfläche des Ringes oder - weil dessen Breite gleich eins ist - durch den Umfang 2π · r dividiert. Es ist also:

|
Zieht man nun, wie es Spitaler tut, eine am Breitekreis festliegende Flächeneinheit in Betracht, so wird diese unter dem Bestrahlungsmeniskus gleiten und von Sonnenaufgang t1 bis Sonnenuntergang t2 ihrer täglichen Bestrahlungsmenge teilhaftig werden, die durch das Integral

|
veranschaulicht ist.
Dies ist ein Zeitintegral, weil bei der am Breitekreisring festliegenden Flächeneinheit die Zeit t die unabhängige Veränderliche des soeben geschilderten Vorganges ist. Auch hier werden die Integrationsgrenzen aus der Forderung dW ⁄ dt = 0 gewonnen.
Um von dem vorstehenden Zeitintegral auf das vorherige den Bestrahlungsmeniskus veranschaulichende Flächenintegral zu gelangen, muss man von Zeitmass auf Bogenmass übergehen, d.h. berücksichtigen, dass die in Zeitmass ausgedrückte geographische Länge durch den Ausdruck

|
veranschaulicht ist. Setzt man dies in das vorstehende Integral ein, so bekommt man:

|
in vollständiger Uebereinstimmung mit der vorher abgeleiteten Formel.
Diese Formel, in der zur Ueberraschung Spitalers im Nenner die Zahl 2π tatsächlich vorkommt und nach dem soeben gesagten vorkommen muss, bildet die Grundlage aller mathematisch einwandfreien Untersuchungen über die Bestrahlung der Erde durch die Sonne. Diese Formel ist nicht nur von Wiener und mir, sondern auch von Hargreaves, Baur und Philips verwendet worden, um mit Hilfe derselben auch den jährlichen Gang der Erdbestrahlung mathematisch zu veranschaulichen. Dies führte bei Wiener zu elliptischen Integralen, bei Hargreaves und mir zu Reihenentwicklungen. Alle diese Untersuchungen führten, wie im vierten Abschnitt dieses Buches bereits festgestellt, zu vollkommen übereinstimmenden Ergebnissen. Diese Ergebnisse stimmten auch, wie dies aus der klassischen Abhandlung von Wiener ersichtlich, mit den früheren Berechnungen von Lambert und Meech überein; die Berechnungen von Angot führten ebenfalls zu denselben Resultaten. Die Berechnungen von Spita1er sind hingegen mit jenen der acht genannten Forscher nicht in Einklang zu bringen; warum, das ist jetzt deutlich sichtbar: weil Spita1er von einem Zeitintegral auf ein Flächenintegral übergehend, die Fundamentalrelation zwischen dem Zeitmasse und dem Bogenmasse, in der das verfluchte 2π vorkommt, unberücksichtigt gelassen hat.
Es bedarf wohl keines weiteren Beweises, dass ein Forscher, der dreissig Jahre braucht, um die Unrichtigkeit seiner Berechnungen einzusehen, und der bei einem neuen Anlauf, das gestellte Problem zu lösen, schon bei der Berechnung der täglichen Strahlungsmenge stolpert, nicht die Fähigkeiten besitzt, ein mathematisch so verschlungenes Problem, wie es jenes der Eiszeiten ist, zu bewaltigen. Nach den Spitalerschen Berechnungen, die, wie jetzt einleuchtend, von Anfang bis Ende fehlerhaft sind, hätten die Eiszeiten Günz, Mindel, Riss und Würm ihre Höhepunkte zu folgenden vier Epochen erreicht: 1.260.000, 890.000, 520.000 und 155.000 Jahren vor der Gegenwart, d.h. in fast genau gleichen gegenseitigen Abständen von 370.000 Jahren. Wie weit auch dies von den tatsächlichen Verhältnissen entfernt ist, wird man aus den nachstehenden Ausführungen klar ersehen.
Die wichtigsten der vorstehend angeführten Theorien der Eiszeiten sind bereits von Hann im ersten Bande seines bekannten "Handbuches der Klimatologie" ausführlich und kritisch besprochen worden, wobei er zum Schlussergebnis gelangte, dass diese Theorien leistungsunfähig sind und man nach denselben eher auf eine gewisse Beständigkeit der irdischen Klimate schliessen müsste. Jetzt wird es klar, warum Hann zu diesem Urteil gelangte. Allen diesen Theorien haftet, wie vorstehend gezeigt, derselbe Fehler an, da keine von ihnen die Veränderlichkeit aller astronomischen Elemente, die den Bestrahlungszustand der Erde beinflussen, richtig erfasst hat. Schon die von Hann vorgenommene Gruppierung dieser Theorien, die nach dem jeweils berücksichtigten astronomischen Element durchgeführt wurde, zeigt deutlich ihre Unzulänglichkeit. Ueberdies hat keine von diesen Theorien den ausschlaggebenden Einfluss der Aenderungen der Ekliptikschiefe auf den Bestrahlungszustand der Erde mathematisch erfassen können. Dieser Einfluss ist erst durch die Ausrechnung der vorstehend mitgeteilten Tabellen XII und XlIl, deren erste Veröffentlichung in meiner akademischen Abhandlung "Ueber die Frage der astronomischen Theorien der Eizeiten" im Jahre 1914 erfolgte, klargelegt worden. In derselben habe ich gezeigt, dass das astronomische Problem der Eiszeiten viel komplizierter ist, als man es vorher angenommen hatte und dass, um zu einer richtigen Lösung zu gelangen, das ganze Problem an seiner Wurzel erfasst und auf eine breite Basis gestellt werden müsse. Wie dies geschehen ist, soll im nachstehenden gezeigt werden.
Kapitel XX
Verlauf der Erdbestrahlung während der letztverflossenen 600 Jahrtausende
§ 114. Vorfragen. Der lange Weg, den ich auf dem Gebiete der exakten Wissenschaften gegangen bin, hat mich zur Etappe geführt, von der aus ich die Veränderungen, die die Erdbestrahlung während der letztverflossenen 600 Jahrtausende erfahren hat, zu überblicken und mathematisch zu erfassen in der Lage bin. Ich habe im Kapitel XV dieses Buches gezeigt, dass sich die säkularen Veränderungen der Erdbestrahlung als eindeutig gegebene Funktionen folgender Grössen darstellen lassen: der Schiefe ε der Ekliptik, der Exzentrizität e der Erdbahn, der Länge Πγ des Perihels, der Solarkonstante J0 und der geographischen Breite φ. Die astronomischen Elemente ε, e und Πγ gehorchen den Gesetzen der Himmelsmechanik und ihre Aenderungen können, wie im Kapitel XIV gezeigt, für das hier in Betracht gezogene Zeitintervall der Vorzeit mit der erforderlichen Genauigkeit berechnet werden. Es muss also nur noch die Frage beantwortet werden, ob während des erwähnten Zeitraumes die Grössen J0 und φ ebenfalls Aenderungen erfahren haben, die von Einfluss auf den Bestrahlungszustand der Erde gewesen sind.
Die Solarkonstante J0 ist der mathematische Ausdruck und das Mass der Ergiebigkeit der Wärmeausstrahlung der Sonne. Während des langen Zeitintervalles des Lebenslaufes unserer Sonne, das mit vielen Jahrmilliarden zu bewerten ist, war die Ergiebigkeit der Sonnenstrahlung langsam verlaufenden Aenderungen unterworfen. Nach dem von Hertzsprung und Russe1 entdeckten Zusammenhang zwischen dem Spektraltypus und absoluter Grössenklasse der Fixsterne und nach den Ergebnissen einer wohlbegründeten Theorie, um deren Ausbau sich hauptsächlich Bialobjevski und Eddington verdient gemacht haben, erscheint es als erwiesen, dass allen Fixsternen ein gleichverlaufender Lebensweg eigen ist. In seinem Anfangsstadium ein riesiger Gasball, weist jeder Stern in seiner Kindheit zwar eine niedrige Temperatur auf, sendet aber wegen seiner Grösse ungeheuere Mengen strahlender Energie in den Weltraum aus. In seiner weiteren Entwicklung schrumpft der Stern allmählich zusammen, seine Ausstrahlung bleibt aber wegen seiner steigenden Temperatur nahezu unverändert, bis bei einer gewissen Dichte sein Temperaturmaximum erreicht wird. Von da an nimmt auch die Temperatur und damit auch die Ausstrahlung des Sternes dauernd ab, er hat den Höhepunkt seiner Entwicklung überschritten und er schreitet auf dem absteigenden Aste seines Lehensweges als Zwerg seinem endgültigen Schicksal entgegen. Unsere Sonne hat jenen Höhepunkt bereits überschritten und ihre Ausstrahlung ist im Sinken begriffen. Ueber das Ausmass uvd die Geschwindigkeit dieser Abnahme der Sonnenstrahlung lassen sich noch keine zahlenmässige Angaben machen.
Alles spricht dafür, dass auch unsere Erde einst ein glühender Gasball gewesen ist, der durch Ausstrahlung ebenfalls grosse Wärmemengen an den interplanetarischen Raum abgab, bis an seiner Oberfläche der feuerflüssige Zustand erreicht wurde, der sich infolge Versinkens abgekühlter Massen auch gegen das Erdinnere ausbreitete. Durch fortgesetzte Abkühlung und Durchmischung wurde auf diese Weise der Erdkern, über dessen damaligen und selbst den gegenwärtigen Aggregatzustand wir nichts bestimmtes wissen, mit einem Mantel geschmolzener Steinmassen umhüllt, deren Temperatur sich infolge der erwähnten Durchmischung nach und nach der Kristallisationstemperatur dieser Massen näherte. Wenn auf diese Weise einmal der Zeitpunkt erreicht würde, zu welchem sich durch weitere Abkühlung an der Oberfläche dieses feuerflüssigen Mantels feste Schollen bildeten, die in dem bereits zähflüssigen Magma nicht versanken, sondern sich zu einer zusammenhängenden Haut vereinigten, änderte sich der Charakter des Abkühlungsprozesses der Erde, denn die weitere Abkühlung konnte, wenn man von dem lokal beschränkten Hervorquellen der flüssigen Massen durch diese dünne und wohl oft geborstene Haut absieht, nur auf dem Wege der Wärmeleitung durch diese feste Erdrinde erfolgen. Dieser Vorgang kann mathematisch verfolgt werden, wie ich dies in meiner "Théorie mathématique" getan habe. Es ergab sich dabei, dass sobald die feste Erdkruste eine Dicke von nur einigen Kilometern erreicht hatte, der aus dem Erdinnern hervorquellende Wärmestrom, durch die geringe Wärmeleitungsfähigkeit jener Kruste gedrosselt, nicht mehr imstande war, den Temperaturzustand der Erdoberfläche zu beeinflussen. Auch die in den Jugendjahren der Erde erhöhte seismische und vulkanische Tätigkeit vermochte nicht diesen Zustand zu ändern, ja selbst die damals stärkere Aktivität der Flutkräfte hatte nach den neueren Untersuchungen bei weitem nicht jenen Einfluss auf den Temperaturzustand der Erde, wie ihn seinerzeit G. H. Darwin nachzuweisen zu haben glaubte. So war also während der ganzen geologischen Vorzeit der Erde die Sonnenstrahlung die einzige Aktivpost im Wärmehaushalt der Erdatmosphäre.
Die geologische Vorzeit der Erde ist nur ein kurzer Zeitabschnitt im Lebenslauf der Sonne, und es muss deshalb die Frage gestellt werden, ob während dieser Vorzeit die Abnahme der Sonnenstrahlung sich fühlbar gemacht habe. Die Ansicht der Geologen und der Klimatologen geht dahin, dass eine Abnahme der Sonnenstrahlung im klimatischen Bilde der geologischen Vorzeit nicht nachweisbar sei, woraus zu folgern ist, dass sich der numerische Wert der Solarkonstante während der geologischen Vorzeit nur unbedeutend geändert haben konnte.
Meine nachstehenden Berechnungen des säkularen Ganges der Erdbestrahlung werden sich, wie gesagt, nur auf die letztverflossenen 600 Jahrtausende erstrecken. Diese Zeitspanne bildet nur einen winzigen Bruchteil der geologischen Vorzeit, weshalb mit Sicherheit anzunehmen ist, dass während dieser Zeitspanne die Solarkonstante sich ganz und gar nicht geändert hat. Deshalb wird bei den nachfolgenden Berechnungen die Grösse J0 als konstant zu betrachten sein. Ich werde sie, wie im vierten Abschnitt dieses Buches bereits mitgeteilt, zur Einheit der zu berechnenden Strahlungsmengen wählen, d. h. J0 = 1 setzen.
Der Frage der Veränderlichkeit der geographischen Breiten ist der ganze dritte Abschnitt des vorliegenden Buches gewidmet. Dort habe ich gezeigt, dass die Lage der Drehpole auf der Erdoberfläche keine fixe ist, diese Pole vielmehr lange Wege auf der Erdoberfläche zurückgelegt haben mssten, wie dies auch durch geologische Forschungen nachgewiesen erscheint. Diese Verlagerung der Drehpole der Erde ging äusserst langsam vor sich. Wie im § 66 mitgeteilt, haben sich diese Pole während der letztverflossenen Jahrmillion kaum mehr als um je l° 20′, d. h. während der letztverflossenen 600 Jahrtausende kaum mehr als um je 48′ auf der Erdoberfläche verlagert. Eine solche Verlagerung des nördlichen Drehpoles der Erde ist zu gering, um den Ablauf des Eiszeitalters, der den Gegenstand der nachfolgenden Untersuchungen bilden wird, bemerkbar zu beeinflussen und hat sich nur während der ältesten zwei Eiszeiten, Günz und Mindel, spürbar gemacht.
Ich werde bei meinen nachfolgenden Berechnungen des säkularen Bestrahlungsganges der Erde die geographische Breite als unveränderlich voraussetzen, um deren Veränderlichkeit erst nachträglich zu berücksichtigen. Dies ist sehr wohl möglich, weil ich meine Berechnungen auf 16 äquidistant verteilte Breiten der Erde erstrecke und durch Interpolation zwischen den Zahlen der derart erhaltenen Strahlungstabelle auch jede Veränderung der geographischen Breite berücksichtigen und die durch dieselbe verursachte Strahlungsänderung mathematisch erfassen kann.
§ 115. Numerische Berechnung des säkularen Verlaufes der Erdbestrahlung. Nachdem die vorstehend gestellten Fragen beantwortet sind, kann auf die Berechnung des säkularen Ganges der Erdbestrahlung geschritten werden. Diese Berechnung erfolgt vermittels der aus dem Newtonschen Gravitationsgesetz und aus dem geometrischen Bestrahlungsgesetz gezogenm Konsequenzen. Diese beiden Gesetze verleihen den nachstehenden numerischen Ergebnissen den Charakter von Dokumenten jener Zuverlässigkeit, wie sie nur die Himmelsmechanik zu gewährleisten imstande ist. Der für die Durchführung dieser dokumentarischen Berechnung erforderliche mathematische Apparat ist im vierten Abschnitt dieses Buches geschaffen und durch die Tabellen XII, XIV und IX für den weiteren Gebrauch bereitgestellt worden,
Wie die analytische Darstellung und numerische Berechnung des säkularen Ganges der Bestrahlung einzelner Breiten der Erdoberfläche zu erfolgen hat, ist im Kapitel XV ausführlich auseinandergesetzt. Man teilt das tropische Jahr in zwei gleich lange, also wirkliche Halbjahre, von denen das eine, das kalorische Sommerhalbjahr, alle jene Tage des Jahres umfasst, an denen die Bestrahlung der in Betracht gezogenen Breite stärker ist als an irgend einem Tage des anderen, des kalorischen Winterhalbjahres, berechnet die diesen Halbjahren zugehörigen Strahlungsmengen Qs und Qw und verfolgt die Aenderungen dieser Strahlungsmengen während des in Betracht gezogenen Zeitraumes der geologischen Vorzeit.
Zum Ausgangspunkt meiner Berechnungen habe ich den Anfang des Jahres 1800 gewählt, weil dieser Zeitpunkt ebenfalls den Ausgangspunkt der Leverrier-Michkovitchen Berechnung der säkularen Aenderungen der astronomischen Elemente bildet.
Die während der kalorischen Halbjahre des Jahres 1800 den einzelnen Rreiten der Erde zugestrahlten Mengen sind in der beiliegenden Tabelle XXIII in kanonischen Einheiten angegeben. Als zu dieser Tabelle zugehörend, ist die Tabelle XXIV berechnet worden, in der die Aenderungen mitgeteilt sind, die die in der Tabelle XXIII enthaltenen Strahlungsmengen während des dem Jahre 1800 nachfolgenden Zeitintervalles von 200 Jahren, also bis zum Jahre 2000 n. Chr. erfahren werden. Man ist also mit Hilfe dieser Tabelle in der Lage, die einem beliebigen Jahre des Zeitintervalles von 1800 bis 2000 entsprechenden, den kalorischen Halbjahren dieses Jahres zugehörigen Strahlungsmengen durch Interpolation zu berechnen. Wie aus dieser Tabelle ersichtlich, sind die Aenderungen der den kalorischen Halbjahren zugehörigen Strahlungsmengen recht klein. Dies gilt jedoch nur für das neunzehnte und zwanzigste Jahrhundert unserer Zeitrechnung, weil, wie aus der Tabelle VIII ersichtlich, die Grösse sin Πγ vor 0,6 Jahrtausenden und die Grösse ε vor 10 Jahrtausenden ihr Maximum überschritten haben und deshalb die säkularen Aenderungen dieser beiden Grössen noch klein sind.
Für längere geologische Zeitintervalle muss man sich der im § 91 angegebenen Rechnungsweise bedienen. Wie dort gezeigt, sind die Aenderungen, die die in der Tabelle XXIII enthaltenen Strahlungsmengen im Laufe der geologischen Vorzeit erfahren haben, durch die Gleichungen (187) und (188) des vierten Abschnittes dieses Buches, also durch
| (1) |

|
|
| (2) |

|
gegeben. Diese Aenderungen entsprechen der Reihe nach den vier Kolumnen der Tabelle XXIII. Dabei sind die den einzelnen Breiten zugehörigen numerischen Werte der Grössen ΔWs und ΔWw der Tabelle XII, und jene der Grösse m der Tabelle XIV zu entnehmen. Die den einzelnen Zeitpunkten der geologischen Vorzeit zugehörigen numerischen Werte von Δε und Δ(e sin Πγ) sind in der Tabelle IX enthalten.
Aus den vorstehenden Gleichungen folgt:
| (3) |

|
welche Gleichung zur Kontrolle der durch die Berechnung erhaltenen numerischen Resultate dienen kann.
Die durch die vorstehenden Formeln berechneten Zahlen geben die gesuchten Strahlungsänderungen in kanonischen Einheit wieder, wie diese im § 85 definiert worden sind. Der klimatische Effekt einer solchen kanonischen Einheit wird aus den Ausführungen des Kapitels XXII ersichtlich werden.
Auf die soeben geschilderte Weise ist die nachstehende Tabelle XXV des säkularen Ganges der Erdbestrahlung berechnet worden, in der die Aenderungen der während der kalorischen Halbjahre den einzelnen Breiten zugestrahlten Wärmemengen enthalten sind.
Diese Tabelle bildet eine Zusammenfassung der in meiner "Mathematischen Klimalehre" veröffentlichten Tabelle 15, in der der säkulare Gang der Bestrahlung der aussertropischen Breiten dargestellt ist, und der in meinen "Astronomischen Mitteln" veröffentlichten Tabelle 92, die sich auf die tropischen Breiten bezieht. Bei der vorliegenden Zusammenfassung dieser beiden Tabellen sind deren numerische Daten noch einmal überprüft und an einzelnen Stellen korrigiert worden. Diese Korrekturen betrafen folgendes.
Wie im § 84 erwähnt, hat von Bacsák in der von Michkovitch berechneten astronomischen Tabelle IX zwei auf das Glied Δ(e sin Πγ) und die Zeitpunkte 500 und 465 sich beziehende Rechen- oder Schreibfehler entdeckt, die neben der in dieser Tabelle erforderlichen Korrektur auch eine solche in der erwähnten Tabelle 15 erheischten.
Ich habe zur Zeit als ich die Berechnung der Tabelle 15 meiner "Mathematischen Klimalehre" bewerkstelligte, die durch die Gleichung (162) des vierten Abschnittes des vorliegenden Werkes dargestellte Summenformel noch nicht entdeckt gehabt, sonndern habe die durch die Formel (168) gegebene Konstante m durch Summierung der in der Tabelle VI enthaltenen Koeffizienten b0, b1, b2, ... berechnet, was zu einer leichten Divergenz zwischen der in der "Mathematischen Klimalehre" auf Seite 51 mitgeteilten Tabelle der Koeffizienten m und der hier mitgeteilten Tabelle XIV Anlass gab. Bei der Berechnung der nachstellenden Tabele XXV sind die numerischen Werte der Tabelle XIV zur Anwendung gekommen, weshalb diese Tabelle an einzelnen Stellen Abweichungen von der Tabelle 15 der "Mathematischen Klimalehre" aufweist, die bei den geographischen Breiten von 5° bis 65° den Betrag von einer kanonischen Einheit nicht übersteigen. Für die Breite von 75° ist die Abweichung grösser; sie erreicht bei dem Zeitpunkte von 445 Jahrtausenden den Betrag von 13 kanonischen Einheiten, sonst ist sie überall kleiner.
Bei der mittels der vorstehenden Gleichung (3) durchgeführten Ueberprüfung der Tabelle 15 der "Mathematischen Klimalehre" hat A. Penck einige Additionsfehler entdeckt, die in der nachstehenden Tabelle XXV ausgemerzt worden sind. Ich danke Herrn Penck, mich auf dieselben aufmerksam gemacht zu haben. Mit diesen Fehlern, die sich auf die südliche Hemisphäre der Erde, und wo dies nicht der Fall ist, auf das Winterhalbjahr der nördlichen Hemisphäre beziehen, ist keine meiner in der "Mathematischen Klimalehre" veröffentlichten Strahlungskurven behaftet, sonst würden solche Additionsfehler sofort zum Vorschein gekommen sein und wären beseitigt gewesen.
Die Tabelle XXV stellt die in mathematischer Sprache verfasste Geschichte der Bestrahlung der Erde durch die Sonne für das Intervall der letztverflossenen 600 Jahrtausende, also einen sogenannten Kanon dieser Bestrahlung dar.
Diese Tabelle ist durch die nachfolgende Tabelle XXVI ergänzt, in der die säkularen Verlagerungen des kalorischen Aequators während des in Betracht gezogenen Zeitintervalles der geologischen Vorzeit angegeben sind. Wie aus dieser Tabelle ersichtlich, waren diese Verlagerungen nicht unbeträchtlich, da sie den Betrag von 8° 37′ erreichten. Während des erwähnten Zeitraumes der geologischen Vorzeit hat der kalorische Aequator dreizehnmal den Breitekreis von +5° und vierzehnmal den Breitekreis von -5° überschritten. In jedem solcher Fälle fand an dem einen oder dem anderen dieser Breitekreise eine Inversion der Jahreszeiten statt. Die Strahlungsmenge, die dem Sommerhalbjahr der in Betracht gezogenen Hemisphäre entsprach, war an diesem Breitekreis geringer als die Strahlungsmenge des Winterhalbjahres. Dies stimmt auch mit dem Ergebnis der Tabellen XXIII und XXV überein. Fügt man den in der Tabelle XXIII mitgeteilten Strahlungsmengen der kalorischen Halbjahre ihre durch die Tabelle XXV gegebenen säkularen Aenderungen hinzu, dann ergibt sich in jenen siebenundzwanzig Fällen für die sommerliche Bestrahlung des in Rede stehenden Breitekreises ein geringerer Betrag als für die winterliche, d. h. an diesem Breitekreis fand sein Sommerhalbjahr zur Zeit des Winterhalbjahres seiner Hemisphäre statt. Der Breitekreis gehörte thermisch seiner Hemisphäre nicht, sondern der anderen Hemisphäre an, weil er vom kalorischen Aequator überschritten war.
Die säkularen Aenderungen jener Breiten, die in der Tabelle XXV nicht enthalten sind, können durch Interpolation zwischen den nächstliegenden Breiten leicht ermittelt werden. Für die äquatornahen Breiten ist dabei neben dem soeben gesagten noch zu berücksichtigen, dass das Sommerhalbjahr der nördlichen Hemisphäre mit dem Winterhalbjahr der südlichen, das Sommerhalbjahr der südlichen Hemisphäre mit dem Winterhalbjahr der nördlichen zusammenfällt, also die Interpolation zwischen den derart zugehörigen Strahlungsmengen zu erfolgen hat.
Kapitel XXI
Die Strahlungskurven als Grundlage der Chronologie und der Vollgliederung des Eiszeitalters
§ 116. Die Strahlungskurven und ihre erste Anwendung. Durch die Ergebnisse der Kapitel XV und XX wurde der Verlauf der Erdbestrahlung während des Zeitintervalles der letztverflossenen 600 Jahrtausende analytisch erfasst und numerisch dargestellt. Es unterliegt keinem Zweifel, dass dieser Bestrahlungsgang so verlaufen ist wie vorstehend geschildert, sind doch zu seiner Erfassung keine Hypothesen erforderlich gewesen, sondern nur anerkannte und wohlerprobte Lehren der astronomischen Wissenschaft. Aus diesem Grunde kann ich, und darin stimmt A. Penck mit mir überein, die vorstehenden Rechnungsergebnisse als den Kanon der Erdbestrahlung bezeichnen.
Mit diesem Kanon kann an die Erforschung des Eiszeitenphänomens geschritten werden. Dabei stehen uns zwei Wege zur Verfügung. Der erste derselben führt, wie der bisher gegangene, über das Gebiet der exakten Wissenschaften. Die im fünften Abschnitt dieses Buches mitgeteilten Lehren dieser Wissenschaft ermöglichen, den dem säkularen Bestrahlungsgang zugehörigen Temperaturgang rechnerisch zu ermitteln und auf diese Weise die dadurch verursachten vorzeitlichen Aenderungen des Erdklimas mathematisch zu beschreiben. Der zweite Weg führt über das Gebiet der beschreibenden Naturwissenschaften. Die Spuren, die die klimatischen Aenderungen der Vorzeit am Antlitz der Erde hinterlassen haben, ermöglichen, wie im § 111 bereits mitgeteilt, die empirische Ermittlung der Aufeinanderfolge der Klimate jenes Zeitraumes der Erdgeschichte, auf den sich meine vorstehenden Berechnungen des säkularen Ganges der Erdbestrahlung beziehen. Es kann also die Frage gestellt und beantwortet werden, wie jene empirisch gefundenen Klimaschwankungen mit diesem theoretisch ermittelten Bestrahlungsgang übereinstimmen. Dieser zweite Weg ist früher als jener zuerst erwähnte betreten worden. Dies geschah, wie ich dies im Vorwort bereits erzählt habe, auf folgende Weise.
Ich habe schon in meiner "Théorie mathématique" nachweisen können, dass die vorzeitlichen Aenderungen der Erdbestrahlung einen mächtigen Einfluss auf den Ablauf der Erdklimate ausgeübt haben mussten. Dieses Ergebnis meines Erstlingswerkes lenkte auf sich die Aufmerksamkeit des grossen deutschen Klimatologen W1adimir Köppen. Er arbeitete damals mit seinem Schwiegersohne A1fred Wegener an dem hier bereits angeführten und noch öfter zu erwähnenden Werke "Die Klimate der geologischen Vorzeit", dessen letztes und grösstes Kapitel "Klimate des Quartärs6quot; er zu bearbeiten übernahm. Dabei gedachte er, den von mir theoretisch errechenbaren Bestrahlungsgang der Erde zur Erforschung des Klimas dieses Abschnittes der Vorzeit zu benützen. Ich wurde also von diesen beiden Gelehrten zur Mitarbeit an ihrem Werke eingeladen und nach brieflichem Gedankenaustausch wurde mir die Aufgabe zuteil, den Verlauf der Bestrahlung der hohen nördlichen Breiten der Erde während der letztverflossenen 650 Jahrtausende numerisch und graphisch zu veranschaulichen.
Bevor ich an diese Arbeit gehen konnte, musste eine prinzipielle Vorfrage gelöst werden, nämlich jene, um welches meteorologische Element und um welche Jahreszeit handelte es sich bei dem Eiszeitalter.
Nach einer erschöpfenden Diskussion aller in Betracht zu ziehenden Umstände beantwortete Köppen diese Frage dahin, dass für die Vergletscherung die Abminderung der Wärme des Sommerhalbjahres entscheidend ist. Dieser Auffassung, die heute wohl von allen Klimatologen vertreten wird, stimmte auch der ebenfalls bedeutende Klimatologe und Mitarbeiter Penks Ed. Brückner in einer ausführlichen Besprechung des Köppen-Wegenerschen Werkes bei: "Schlagend zeigen die obigen Zahlen, dass es nur die niedrigen Sommertemperaturen sind, die die Vergletscherung erzeugen. Kalte Sommer in grosser Häufung müssen also als Ursache der Vergletscherung und der Bildung des Inlandeises betrachtet werden."
Zu demselben Ergebnis gelangte, wie nachstehend gezeigt werden wird,auch ich auf einem anderen Wege, den mir die Erforschung des Zusammenhanges zwischen Erdbestrahlung und Schneegrenze und jenes zwischen Einstrahlung und Temperatur eröffnete, den ich aber zur Zeit der Abfassung des Köppen-Wegenerschen Werkes noch nicht betreten hatte. Es war deshalb das grosse Verdienst Köppens, mir in dieser Frage den richtigen Weg gezeigt zu haben, indem er mir riet, bei meinen Berechnungen das Augenmerk auf die Zeiten mit kalten Sommern zu richten.
Bevor ich diese Berechnungen in Angriff genommen hatte, habe ich durch die Aufstellung des Begriffes der kalorischen Jahreszeiten das Mittel gefunden, die säkularen Aenderunden der Erdbestrahlung mathematisch zu erfassen und darzustellen. Seidem habe ich den hiezu erforderlichen mathematischen Apparat vervollständigt und ihm die im Kapitel XV mitgeteilte Form gegeben. Immerhin war das damals von mir von diesem Apparat geschaffene ausreichend, der gestellten Aufgabe gerecht zu werden.
Die durch die Formeln (185) des vierten Abschnittes dieses Buches veranschaulichten Aenderungen der Bestrahlung der in Betracht gezogenen geographischen Breite erreichen, weil sich die Perihellänge Π, schneller ändert als die Schiefe e der Ekliptik, mit grosser Annäherung ihre extremen Werte zu den Zeiten, zu denen die Perihellänge Π den Wert von 90° bzw. 270° aufweist. In diesen beiden Fällen sind die dem kalorischen Sommer- bzw. Winterhalbjahr zugehörigen Strahlungsmengen vermittels der Gleichungen (126) und (171) des erwähnten Abschnittes durch die nachstehenden Formeln gegeben:

|
wobei das obere Vorzeichen für Πγ = 90°, das untere für 1Πγ = 270° gilt.
Mit den vorstehenden Formeln lassen sich die einzelnen Ausschläge des Bestrahlungsganges der in Betracht gezogenen geographischen Breite berechnen und man kann mit diesen Formeln das Hin- und Herschwenken der Bestrahlung dieser Breite in die Vorzeit verfolgen.
Meine diesbezüglichen Berechnungen führte ich betreffs der sommerlichen Wärmemengen, die während des in Betracht gezogenen Zeitraumes der Vorzeit den nördlichen Breiten von 55°, 60° und 65° zugestrahlt wurden. Dabei bediente ich mich hinsichtlich der säkularen Veränderungen der astronomischen Elemente der in der Tabelle VIII mitgeteilten von Pilgrim berechneten Zahlenwerte. Nachdem ich auf diese Weise die gewünschten Strahlungsänderungen berechnet hatte, setzte ich im Einverständnis mit Köppen diese Aenderungell in fiktive Breiteschwankungen um, weil wir dadurch ein geometrisches Bild dieser Aenderungen gewinnen wollten. Hatte sich also beispielsweise für den Breitekreis von 65° und für einen bestimmten Zeitpunkt der geologischen Vorzeit eine Verminderung der sommerlichen Strahlungsmenge gegenüber der heutigen ergeben, so ermittelte ich jene nördlicher gelegene Breite, auf die man sich gegenwärtig zu begeben hätte, um durch diese Aenderung der Breite die berechnete Abminderung der sommerlichen Strahlungsmenge zu erreichen. Einer Vermehrung der sommerlichen Strahlungsmenge entsprach eine fiktive Breiteschwankung nach Süden.
Auf diese Weise erhielt ich drei zackenförmige Linien, die man später "Strahlungskurven" nannte und die ich zu einem Diagramm vereinigte, das dem Köppen-Wegenerschen Werke auf einer besonderen Tafel beigefügt wurde, während meine diesbezüglichen Erläuterungen im Text des Buches Aufname fanden.
In der beiliegenden Fig. 48, obere Abbildung, ist die auf die geographische Breite von 65° sich beziehende und bis zum 600. Jahrtausend vor der Gegenwart reichende Zackenlinie des erwähnten Diagrammes wiedergegeben. Die auf die Breiten von 55° und 60° sich beziehenden Zackenlinien sind in der Fig. 48 nicht wiedergegeben, weil diese fast gleichverlaufend mit jener von 65° sind. In derselben Figur ist durch die untere Abbildung die Strahlungskurve wiedergegeben, wie sie sich mit Benützung der in der Tabelle IX mitgeteiten Zahlen ergeben hat.

Betrachtet man die obere, Köppen zur Verfügung gestellte Zackenlinie der Fig. 48, so erkennt man darin neun besonders starke Abminderungen der sommerlichen Bestrahlung, die zu den Zeiten von 589, 548, 475, 434, 231, 187, 116, 72 und 22 Jahrtausenden vor der Gegenwart stattgefunden haben. Diese neun Kälteeinbrüche erscheinen zu vier Gruppen vereinigt, von denen die ersten drei je zwei Zacken aufweisen, die vierte deren drei besitzt In diesen vier Gruppen erkannte Köppen die vier Eiszeiten des Penck-Brücknerschen Schemas, die Günz-, die Mindel, die Riss und die Würm-Eiszeit.
Als ich bei der Abfassung meiner "Mathematischen Klimalehre" die Berechnung des säkularen Ganges der Erdbestrahlung auf eine breitere Basis stellte und diese Berechnung mit Benützung der Zahlenwerte der Tabelle IX, also mit besseren Massenwerten der Planeten durchführte, entwarf ich eine der im Köppen-Wegenerschen Werke veröffentlichten ähnlichc Strahlungskurve, die in der Fig. 48 durch die untere Abbildung veranschaulicht ist. In dieser neueren Kurve ist der in die Zeit von 22 Jahrtausenden vor der Gegenwart fallende letzte Einbruch sommerlicher Kälte, der in der alten Kurve schwächer ausgebildet ist, durch eine deutlich ausgebildete starke Zacke veranschaulicht. Dies veranlasste mich, die auf diesen Zeitpunkt sich beziehende Berechnung Pilgrims einer Kontrolle zu unterziehen und da ergab sich, dass die auf den Zeitpunkt von 22,3 Jahrtausenden vor der Gegenwart und auf die Schiefe der Ekliptik sich beziehende Berechnung Pilgrims mit einem Rechenfehler behaftet erscheint, so dass die in der Tabelle VIII enthaltene diesbezügliche Zahl von 22° 44′ durch 22° 33′ zu ersetzen ist. Die daraus resultierende Korrektur ist in der beiliegenden Abbildung durchgeführt worden.
Vergleicht man die beiden in der Fig. 48 wiedergebenen Diagramme miteinander, so ersieht man, dass sie gut übereinstimmende Resultate liefern: in beiden Diagrammen kommen die erwähnten neun stärksten Einbrüche sommerlicher Kälte zu denselben bereits angegebenen Zeiten deutlich zum Verschein. Die noch vorhandenen kleineren Abweichungen rühren mit Ausnahme der im § 84 erwähnten auf die Zeitpunkte 500 und 465 sich beziehenden von den verschiedenen Massenwerten der Planeten her, die den Berechnungen von Stockwell bzw. jenen von Michkovitch zugrunde lagen. Das Ausmass dieser Abweichungen ist, wie im § 84 bereits gesagt, eine Bürgschaft dafür, dass die eventuell noch sich als notwendig erweisenden Korrekturen der Planetenmassen den hier berechneten Verlauf der vorzeitlichen Aenderungen der Erdbestrahlung nur unwesentlich zu beeinflussen imstande sein werden.
Kehren wir nochmals zu der in der Fig. 48, untere Abbildung, wiedergebenen Strahlungskurve zurück! Wenn man darin alle über 68° reichenden Zacken durch Schraffieren kennzeichnet, so ersieht man deutlich, dass sie die übrigen Zacken des Diagramms deutlich überragen. Fasst man diese Zacken zu den angegebenen vier Gruppen zusammen, so bekommt man das in der beiliegenden Fig. 49 dargestellte Schema.

Vergleicht man nun die beiden durch die Fig. 49 bzw. die Fig. 47 (Seite 491) dargestellten Schemas miteinander, so ersieht man, dass sie sehr gut, ja verblüffend übereinstimmen, wenn man bedenkt, dass sie auf ganz verschiedenen Wegen, durch geologische Forschung bzw. durch astronomische Berechnung, gewonnen worden sind. Auf diese Uebereinstimmung, die sich auch bei Benützung des älteren Diagramms offenbarte, hinweisend, konnte Köppen mit aller Entschiedenheit behaupten, dass sich in meinen Strahlungskurven die vier alpinen Eiszeiten getreulich widerspiegeln, welcher Erkenntnis bald nachher auch Brückner in seiner bereits erwähnten Abhandlung beipflichtete.
Auf diese Weise hat Köppen als erster den Zusammenhang zwischen dem von mir mathematisch erforschten säkularen Bestrahlungsgang der Erde und den nachgewiesenen erdgeschichtlichen Klimaten mit genialem Blicke entdeckt
Um seiner Behauptung eine feste Grundlage zu geben, musste Köppen noch die Frage klären, wie die durch das Zeitintervall wärmerer Sommer getrennten je zwei oder drei Einbrüche sommerlicher Kälte den Eindruck je einer einheitlichen "Eiszeit" hinterlassen konnten.
Heute ist man, wie aus dem nachfolgenden Kapitel ersichtlich werden wird, in der Lage, viel weitgehendere Schlüsse aus dem Verlauf des säkularen Bestrahlungsganges zu ziehen als es aus der obigen ersten graphischen Darstellung dieses Ganges möglich war. Man kann beispielsweise nicht nur qualitativ, sondern auch quantitativ angeben, wie sich durch diesen Gang die Schneegrenze hin und her verschieben und die polare Eiskalotte verbreiten und zusammenschrumpfen hat müssen. Es ist deshalb möglich, auch die Frage zu beantworten, warum in den Zentren der Vereisungen, in den Alpen und den Polargegenden, die eng benachbarten Kältevorstösse den Eindruck je einer Eiszeit hervorrufen mussten. Das zur Beantwortung aller dieser Fragen erforderliche mathematische Werkzeug war aber damals, als Köppen und Wegener ihr Buch schrieben, noch nicht geschmiedet, und es ist deshalb erstaunlich, wie treffend Köppen die gestellte Frage beantwortete und seine Behauptung bewies.
In seinem und Wegenerschem Werke konnte Köppen auch auf die ausgezeichnete Uebereinstimmung des aus der Strahlungskurve bei dem Jahrtausend 11 klar ersichtlichen Maximums der sommerlichen Bestrahlung mit dem durch die geologische Forschung festgestellten Klimaoptimum hinweisen. Er konnte sich auch darauf berufen, dass, wie erwähnt, noch vor der Veröffentlichung dieser ersten Strahlungskurven eine Dreiteilung der Wurm-Eiszeit bereits festgestellt war und konnte mit der Stimme des Propheten verkünden, es mehren sich die Anzeichen dafür, dass man selbst in den Alpen die Spaltung der Eiszeiten in mehrere Hauptvorstösse noch erkennen wird. Und dies sollte sich, wie man sogleich sehen wird, bald bewahrheiten.
§ 117. Die Zergliederung des alpinen Glazials. Nach seiner Veröffentlichung im Köppen-Wegenerschen Werke wurde das von mir entworfene Strahlungsdiagramm, dessen einzelne Zackenlinien man, wie bereits erwähnt, Strahlungskurven nannte und mit meinem Namen — anfangs auch mitunter mit den Namen von Köppen und Wegener — bezeichnete, auch von anderen Gelerten bei ihren Forschungen benützt, um die gewonnenen Befunde in die Strahlungskurve einzuordnen und dadurch astronomisch zu datieren. Und dies ist auch ferner so geschehen.
Es entspricht dem Zweck und der Anlage dieses Werkes, auch über alle auf meine Strahlungskurven bezugnehmenden Arbeiten kurz zu berichten, weil dadurch die praktische Verwendbarkeit dieser Kurven und die Reichweite der ihnen zugrunde liegenden Theorie am deutlichsten zu Tage treten wird.
Ich beginne meinen Bericht, der wegen des grossen und ständig zunehmenden Materials weder auf Vollständigkeit noch auf systematische Anordnung Anspruch erheben kann, mit einem Werke, das die im vorhergehenden Paragraphen angeschnittene Gliederung der alpinen Vereisung zum Gegenstand hat; es ist das umfangreiche Werk von Barthe1 Eberl über die Eiszeitenfolge im nördlichen Alpenvor1ande.
Das eigentliche Forschungsgebiet von Eberl ist, wie dies im Untertitel des Werkes angegeben wird, die Eiszeitlandschaft des nördlichen Alpenvorlandes und zwar der Raum zwischen Lech und Iller, die von Penck so benannte Lech-Illerplatte. Hier haben zwei kleinere Gletscher, der Lech- und der Illergletscher, mit ihren Eiszungen den Raum gefüllt, mächtig genug, um die ganze Phasenfolge der Eisvorstösse zur Entwicklung zu bringen, und doch nicht so übermächtig, dass sie immer wieder die eigenen Ablagerungen weithin zerstört oder überschattet hatten, wie dies in Gebieten mit besonders grossartiger Entwicklung der aus den Alpen quellenden Eisströme gewöhnlich geschah. Auf diesem Gebiete des Alpenvorlandes ist die eiszeitliche Schichtenfolge nicht nur vollständig entwickelt, sondern auch wunderbar erhalten und hier ist es Eberl durch Verfeinerung der Methoden und Intensivierung der Beobachtung gelungen, alle Phasen der alpinen Vereisung in einem so weitgehenden Masse zu erkennen und nachzuweisen, wie es kaum anderswo geschehen konnte. Da ergab es sich aus der Gliederung der Moränen und Schotter, dass die Eiszeiten Günz, Mindel und Riss doppelphassig waren, während sich in der Würm-Eiszeit drei Hauptstösse kundgaben.
Durch dieses Ergebnis, über das Eberl in seinem Vortrag in der Geologischen Vereinigung zu München bereits am 29. Januar 1924, also noch vor der Veröffentlichung meiner Strahlungskurven berichtete, wurde die Mehrgliederung der alpinen Eiszeiten, wie sie Köppen aus dem Verlauf der Strahlungskurve vorhersagte, auf das vollständigste bestätigt.
Die Ergebnisse der Untersuchungen von Eberl, wie sie in ihrer Vollständigkeit in seinem soeben erwähnten Werke veröffentlicht erscheinen, sind aber noch viel weitgehender. Er veranschaulichte sie nämlich durch ein stratigraphisches Diagramm, das ich hier in der beiligenden Fig. 50 wiedergebe. In demselben ist der Ablauf und die räumliche Entwicklung der vorzeitlichen Vergletscherungen des durchforschten Gebietes graphisch dargestellt. Durch die Ordinaten dieses Graphikons ist die Reichweite der einzelnen Gletschervorstösse veranschaulicht. Diese Ordinaten stellen sichere, durch direkte Beobachtung gewonnene Werte dar, deren reichliches Ausmass von 25 bis 50 Kilometer jeden Zweifel an ihre Zuverlässigkeit von vorn herein ausschliesst. Die Abszissen des Graphikons beruhen dagegen auf geologischen Schätzungen nach dem Masse der in den Zeiten zwischen den Vereisungen stattgehabten Verwitterung und der Zersägung der Ablagerung durch die Flüsse. Vergleicht man dieses statigraphische Diagramm mit meinem in Köppen-Wegenerschen Buche veröffentlichten Strahlungsdiagramm, das — man wird sogleich erfahren warum — mit seiner nachträglich berechneten Fortsetzung bis zum 1.000. Jahrtausend reichend in der Fig. 51 veranschaulicht ist, so ersieht man folgendes. Alle von Eberl auf dem durchforschten Gebiet festgestellten Gletschervorstösse finden sich in meinem auf astronomischer Grundlage berechneten Strahlungsdiagramm durch entsprechende die Zeiten der kalten Sommer veranschaulichende Zacken getreulich wiedergegeben. Diese Uebereinstimmung der Resultate zweier auf ganz verschiedenem Wege gewonnenen Gliederungen ist geradezu als wunderbar zu bezeichnen, besonders wenn man bedenkt, dass Eber1, wie erwähnt, zu seinen Ergebnissen noch vor der Veröffentlichung meiner Strahlungskurven gekommen ist. Dies gilt auch hinsichtlich des restlichen über das 650. Jahrtausend vor der Gegenwart reichenden Teiles der beiden Diagramme.

Es war nämlich Eberl, wie schon früher Gutzwiller im Sundgau, gelungen, noch ältere, vor der Günz-Eiszeit abgelagerte, sehr verwitterte Schotter zu finden, die in seinem stratigraphischen Diagramm. unter 1 bis 5 eingetragen sind. Als er deshalb die volle Uebereinstimmung seiner übrigen Feststellungen mit dem in Köppen-Wegenerschen Buche bis zum 650. Jahrtausend reichenden Strahlungsdiagramm ersah, wandte er sich durch Vermittlung von Köppen an mich mit der Bitte, mein Strahlungsdiagramm über diesen Zeitpunkt zu verlängern, was auch geschehen ist. Auch diese Teile der beiden Diagramme stimmten, wie ersichtlich, überein: die von Eberl geologisch festgellten Kälteneinbrüche kamen in der von Eberl angegebenen Reihenfolge und Anordnung deutlich zum Vorschein.

Die ausgesprochen glaziale Natur der in diesem Teile des stratigraphischen Diagrammes eingetragenen Schotterablagerungen ist zwar noch nicht ganz sichergestellt, doch sind auch anderswo, nämlich in sämtlichen deutschen Stromgebieten hohe vor-günzische Terrassen gefunden worden, die wahrscheinlich diesen frühen Oszillationen der Erdbestrahlung entsprechen. Auch in Westeuropa gewinnt man den Eindruck, dass zwischen Günz und das typische Tertiär eine ziemlich beträchtliche Uebergangsperiode eingeschaltet sei. Es ist sehr wahrscheinlich, dass vereinzelte Kältevorstösse, wie es die im Strahlungsdiagramm mit I und II bezeichneten gewesen sind, nicht die Wirkung der rasch hintereinander sich wiederholenden gehabt hatten. Sicher ist es aber, dass auch diese kurzandauernde vor-günzischen Vorstösse deutliche Spuren hinterlassen hatten und astronomisch datiert werden konnten. Ihr auf zwei verschiedenen Wegen, auf jenem der geologischen Forschung und jenem der astronomischen Berechnung, erfolgte Nachweis hat auch berechtigtes Aufsehen erregt, wie dies in dem bald zu erwähnenden Artikel von Kei1hack deutlich zum Ausdruck gelangte.
Die Zweiteilung der Günz-, Mindel- und Riss-Eiszeit, sowie die Dreiteilung der Würm-Ablagerungen ist auch von Knauer im Lech-Isar-Gebiet festgestellt worden, und zwar ebenfalls ohne Kenntnis meiner Strahlungskurven. Weil paläontologische und petrographische Hilfsmittel zur Trennung der verschiedenen Gebilde nicht oder meist nicht zur Verfügung standen, hat Knauer vorgezogen, die "überzähligen Gebilde" als Vorrückungs- und Rückzugsstillstände des Eises zu betrachten, hebt aber die nahezu vollständige Uebereinslimmung der Befunde mit der Strahlungskurve hervor. Dasselbe gilt auch für seine späteren auf das norddeutsche Vereisungsgebiet und das westalpine Vorland sich beziehenden Abhandlungen, in denen er auf meine Strahlungskurve oder auf die aus derselben abgeleitete Vereisungskurve von Soergel oder auf beide Bezug nimmt.
Auch Gagel hat lange vor der Veröffentlichung meiner Strahlungskurven auf all die Unstimmigkeiten hingewisen, die sich aus den Beobachtungen über das Diluvium und aus deren Einzwängung in das damals in Gebrauch stehende — und ,wie es sich herausgestellt hat, ganz unzureichende — Gliederungsschema ergaben. Nach der Veröffentlichung der Strahlungskurven erklärte Gagel, dass der grösste Teil dieser Unstimmigkeiten ucd Unbegreiflichkeiten sich auflösen werde und dass eine verständliche und in sich wiederspruchlose Gliederung des Diluviums das Ergebnis sein wird.
Ausser Eberl und Knauer hat sich Paul Beck sehr eingehend mit der Gliederung des alpinen Glazials beschäftigt, nachdem er eingesehen hat, dass mit dem "starren und hemmenden Panzer, den die Penck-Brücknersche Vierheit der Eiszeiten an alle europäischen Forschungen legte" nicht auszukommen ist. Beck durchforschte das Moränengebiet des Aaregletschers in der Schweiz, gelangte dabei zu einer Einteilung in sieben Vereisungen und fand, dass diese Einteilung nach Zahl und Zeitabstand in überraschender Weise mit meiner Strahlungskurve übereinstimmt.
Nachher stellte Beck die Frage, ob die Strahlungsschwankungen allein ausreichend gewesen waren, um die in den Alpen geologisch festgestellten Eisvorstösse in ihrem vollen Umfang zu erzeugen. Er unternahm es also mit Hilfe der in meiner "Mathematischen Klimalehre" veröffentlichten Angaben über den säkularen Gang der Erdbestrahlung und mit Anwendung seines Prinzips der Frostmonate, Anhaltspunkte über die klimatischen Auswirkungen dieses Ganges zu gewinnen und gelangte zu dem Ergebnis, dass die von mir berechneten Strahlungsschwankungen mit den direkten thermischen und hydrometeorischen Folgen in Zusammenhang mit den indirekten Auswirkungen der entstehenden Vergletscherungen genügen, um die grössten Vereisungen der Schweizeralpen zu erklären.
Mit dem Ablauf des alpinen Postglazials hat sich Bertsch eingehend befasst und gefunden, dass das von ihm hauptsächlich auf pollenanalytischem Wege entworfene Bild dieses Ablaufs mit meiner Strahlungskurve übereinstimmt.
§ 118. Die Vollgliederung des Eiszeitalters. Hat der säkulare Gang der Erdbestrahlung deutliche Spuren im Alpengebiet hinterlassen und hat er hier durch die bei den einzelnen Gletschervorstössen geschaffen Endmoränen seine Aussch äge und seinen Rhythmus derart markiert, dass eine weitgehende Zergliederung und eine auf zuverlässiger astronomischer Berechnung fussende Chronologie des alpinen Glazials durchgeführt werden konnte, so gilt dies in noch grosserem Masse für das Randgebiet der norddeutschen Vereisungen. In diesem Randgebiet sind unter vorwiegend klimatischen Bedingtheiten bestimmte Gesteine entstanden, die als glaziale oder interglaziale mit Sicherheit zu erkennen sind und auch eine feste Bezugnahme auf die eigentlichen Vereisungsgebiete gestatten. Als neu oder doch in vollständiger Entwicklung nur dem Randgebiet eigentümlich kommen hinzu die Schotterterrassen und in besonders reicher Gliederung die Lösse, die als sichere Zeugen für wiederholte Herrschaft eines kalten Trockenklimas zu betrachten sind. Und schlieslich müssen Klimaschwankungen im Randgebiet von wesentlichem Einfluss gewesen sein auf die Tätigkeit der Flüsse, auf Erosion und Akumulation. Eine solche klimatische Einflussnahme auf die Flusstätigkeit muss sich wie dies Siegert und Soergel ausführlich dargelegt hatten, besonders geltend machen im Oberlauf der Flüsse, vor Allem in den Oberlaufgebieten der grossen Stromsysteme Deutschlands. Hier müssen alle grösseren Klimaschwankungen in der Flusstätigkeit gewissermassen registriert worden sein.
Ausgehend von dieser Erkenntnis hat Wolfgang Soergel noch vor der Veröffentlichung meiner Strahlungskurven die volle Durchgliederung des Eiszeitalters als Grundaufgabe der Eiszeitforschung erkannt und ihrer Lösung eine ganze Reihe grundlegender Arbeiten gewidmet, weshalb er als der Begründer der Vollgliederung des Eiszeilalters zu betrachten ist.
Die ersten sicheren Anhaltspunkte zu dieser Voligliegerung gewann Soergel in Thüringen im Oberlaufgebiet des Elbsystems. Hier gelang es ihm noch vor dem Bekanntwerden meiner Strahlungskurven nachzuweisen, dass die Flussterrassen der Saale und der Ilm ihre Entstehung Klimaschwankungen verdanken. Jede Aufschotterungsphase entspricht einer Zeit glazialen Klimas, jede Einschneidungsphase einer Zeit gemässigten Klimas. Es ergab sich dadurch eine Gliederung des Eiszeitalters in 11 kalte und 11 gemässigte Perioden.
Zwei Monate nachdem diese Ergebnisse der Soergelschen Forschungen veröffentlicht wurden, erschien das Köppen-Wegenersche Werk, und so konnte Soergel seine Ergebnisse mit meinen in diesem Werke veröffentlichten Strahlungskurven vergleichen und in Beziehung bringen. Dies tat er in seinem bald nachher erschienenem Buche "Die Gliederung und absolute Zeitrechnung des Eiszeitalters". Dabei erweiterte er sein Forschungsgebiet derart, dass bereits in diesem Buche die Vollgliederung der deutschen Flussysteme ihre festen Umrisse erhielt.
Ich kann hier nur die wichtigsten Ergebnisse dieser grundlegenden Arbeit Soergels kurz erwähnen. In der beiliegenden Fig. 52 sehen wir seine Parallelisierung der Schotterterrassen der Ilm mit der untersten Strahlungskurve meines im Köppen-Wegenerschen Werke veröffentlichten Strahlungsdiagramms.

Wie aus dieser Figur ersichtlich, fanden alle grösseren Spitzen der Strahlungskurve ihr Korrelat in den Schotterterrassen der Ilm und zwar nicht nur die neun grössten Spitzen, sondern noch zwei kleinere, die Soergel mit "Prae-Riss" und "Prae-Würm" bezeichnete.
Soergel blieb bei diesem hochwichtigen Ergebnis seiner Forschungen nicht stehen, sondern erweiterte diese auch auf das System der Weser, über dessen diluviale Terrassen Siegert eine ausführliche Studie veröffentlicht hatte. Dabei gelang es Soergel eine ins Einzelne gehende Parallelisierung der Ilm-Salle-Terrassen mit den Werra-Weser-Terrassen durchzuführen und gründete damit seine Gliederung auf die Befunde im Oberlauf zweier selbständigen Stromsysteme.
Um den Ring der Beweise für die Richtigkeit der von ihm durchgeführten Vollgliederung zu schliessen, zog Soergel noch ein reich gegliedertes diluviales Profil heran, um auch dasselbe mit der Strahlungskurve in Beziehung zu bringen. Es war dies das Profil der Schichtenfolge des Süsswasserkalklagers von Ehringsdorf bei Weimar, dessen Stellung in der Vollgliederung des Eiszeitalters und damit auch in der Strahlungskurve durch die zuunterst liegenden Flussschotter ebenso wie durch den zuoberst liegenden Löss bestimmt und sicher eingegrenzt ist. Auch hier ergab sich eine in die feinsten Einzelheiten reichende Uebereinstimmung mit der Strahlungskurve. Deshalb konnte Soergel die Ergebnisse seiner Forschungen zusammenfassend sagen: "Wohl noch selten haben zwei Lösungsversuche für das gleiche Problem, die ganz unabhängig voneinander und auf ganz verschiedener Grundlage unternommen worden sind, zu derartig übereinstimmenden Resultaten geführt. Darin liegt eine sehr hohe Gewahr der in beiden Systemen vertretenen Eiszeitgliederung; beide Systeme stützen sich gegenseitig. Ich halte damit die astronomische Gliederung des Eiszeitalters für bewiesen, das Problem der absoluten Zeitrechnung für gelöst".
Auch nach der Veröffentlichung seines soeben besprochenen Buches war Soergel am weiteren Ausbau der Vollgliederung des Eiszeitalters unermüdlich tätig. Seine diesbezüglichen Untersuchungen sind in einer Reihe von Abhandlungen und in zwei besonderen Veröffentlichungen niedergelegt; die ersteren befassen sich vorwiegend mit Spezialfragen, die ich aber ihrer Wichtigkeit wegen hier anführen muss, die letzteren behandeln das Eiszeitenproblem in seiner Gänze und werden später zu Besprechung gelangen.
Soergels Arbeiten haben Schule gemacht. Eine ständig zunehmende Zahl von tüchtigen Forschern unternahm es, die Quartärablagerungen nach den neuen Gesichtspunkten zu gliedern, mit der Strahlungskurve in Verbindung zu bringen und mit Hilfe derselben zu datieren. Dadurch hat, wie sich einer der besten dieser Forscher mir gegenüber schriftlich äusserte, die Quartärgeologie einen starken Impuls erhalten, da ihr die Möglichkeit geboten wurde, die bisherigen beschreibenden Ergebnisse einem exakten System einzuordnen.
Die von Soergel im thüringischen System hauptsächlich an der Ilm gewonnenen Ergebnisse wurden durch Toepfer auch für die Saale bestätigt, deren glaziale Terrassen Toepfer in die Strahlungskurve einordnete.
Ausser in Thüringen sind, wie wir dies bereits für das Flusssystem Werra-Weser gesehen haben, auch in anderen Gebieten Deutschlands Systeme von Flussterrassen gefunden worden, die sich mit den Oszillationen meiner Strahlungskurven decken und die Soergelsche Vollgliederung bestätigen. Grahmann, der als einer der ersten der astronomischen Theorie der Klimaschwankungen seine Aufmerksamkeit schenkte und bei seinen ausgedehnten Untersuchungen meine Strahlungskurven benützte, erforschte die Terrassen der Elster und Mulde und ordnete sie in die Strahlungskurve ein. Auch in seinen anderen Veröffentlichungen hat er von meinen Strahlungskurven Gebrauch gemacht und hat der astronomischen Theorie der Klimaschwankungen auch dadurch wertvolle Dienste geleistet, dass er als erster den Anschluss der Strahlungskurven an die De Geerschen Warwenzählungen bewerkstelligte.
Steinmann untersuchte das Diluvium des Rheingebietes, das mit einem durchgehenden System von Schotterterrassen das alpine und das nordische Vereisungsgebiet miteinander verknüpft, und fand, dass dessen Gliederung aufs beste mit der Strahlungskurve übereinstimmt.
Beurlen hat in Auschluss an die Arbeiten von Soergel in einer besonderen Studie die geologischen Vorgänge in Ostpreussen während des Diluviums mit den durch die Strahlungskurve dargestellten Klimaschwankungen in Beziehung gebracht und sie in die Strahlungkurve eingeordnet.
Staub besprach die bis zum Jahre 1927 mit der Strahlungskurve erzielten Ergebnisse, durch die eine absolute Zergliederung und Unterteilung des Eiszeitalters auf astronomisch-physikalischen Wege ermöglicht wurde.
Dietrich gab in seiner Studie über den Rixdorfer Horizont ein die Vollgliederung bestätigendes Schema des Berliner Diluviums.
Zeuner hat an den Flussterrassen der Glatzer Neisse in Schlesien zwei Warmphasen, zwei Rissphasen, eine Vor-Riss-Phase und die zweite Mindelphase nachgeweisen und in die Strahlungskurve eingeordnet, wobei ihm das absolute Zeitmass dieser Kurve ermöglichte, die Hebungsgeschwindigkeit des Sudetengebirges zu berechnen.
§ 119. Weitere Anwendungen der Strahlungkurven.
Kapitel XXII
Klimatische Answirkungen des säkularen Ganges der Erdbestrahlung
§ 120. Die unmittelbaren thermischen Effekte des säkularen Ganges der Erdbestrahlung. Die Ergebnisse des fünften Abschnittes dieses Buches setzen mich in den Stand, die thermischen Effekte des säkularen Ganges der Erdbestrahlung mathematisch zu erfassen. Diese Effekte können in unmittelbare und mittelbare unterschieden werden; mit den ersteren habe ich mich bereits in der "Mathematischen Klimalehre" befasst, die letzteren kamen in meinen "Astronomischen Mitteln" zur ausführlicheren Behandlung. Diese Reihenfolge soll auch hier eingehalten werden. Was unter den unmittelbaren, was unter den mittelbaren Effekten des säkularen Ganges der Erdbestrahlung zu verstehen ist, das lässt sich an der Hand der Gleichung (119) des fünften Abschnittes, d. h. der Gleichung
| (4) |

|
deutlich erklären.
Diese Gleichung vermittelt den Zusammenhang zwischen der jahreszeitlichen, ganzjährigen oder halbjährigen, Bestrahlung W der in Betracht gezogenen Breite der Erdoberfläche und der zugehörigen absolut gemessenen Temperatur θ(o) der untersten Luftschicht. Dabei bedeutet A das Reflexionsvermögen der in Betracht gezogenen Flächeneinheit der Erdoberfläche samt der darauf lagernden Atmosphäre, M die Masse dieser atmosphärischen Säule und k2 den zugehörigen Absorptionskoeffizient für die dunklen Strahlungen.
Nehmen wir vorerst an, es habe sich an der in Betracht gezogenen Stelle der Erde nur die jahreszeitliche Bestrahlung W säkular verändert. Dann lässt sich die dadurch verursachte Aenderung der Temperatur θ(o) wie folgt berechnen.
Der gemachten Annahme zufolge sind in der vorstehenden Gleichung die Grössen A und k2 als unveränderlich zu betrachten und es folgt aus den Gleichungen (84) und (140) des vorhergehenden Abschnittes
| (5) |

|
oder, falls man der kürzeren Schreibweise halber
| (6) | n = 14146x106 |
setzt und aus demselben Grunde statt θ(o) einfach θ schreibt,
| (7) | θ4 = n · W. |
Es stelle W die dem in Betracht gezogenen Jahre der geologischen Vorzeit zugehörige jahreszeitliche Bestrahlung und θ die zugehörige jahreszeitliche Temperatur dar, während die auf die Gegenwart sich beziehenden Werte mit W0 bzw. θ0 bezeichnet werden mögen. Es ist dann
| (8) |

|
|
| (9) |

|
Die Differenz
| (10) |

|
stellt die säkulare Aenderung der Bestrahlung W dar und es ist
| (11) |

|
Bezeichnet man die in Celsiusgraden gemessenen auf die Vorzeit bzw. auf die Gegenwart sich beziehenden Temperaturen der untersten Luftschicht mit u bzw. u0, so ist

|
Berücksichtigt man, dass u ⁄ 273 und u0 ⁄ 273 kleine Zahlen sind, so dass ihre Potenzen neben der Einheit vernachlässigt~werden können, dann folgt mit Anwendung der Binomialformel:

|
||
| (12) |

|
Weil
| (13) | u - u0 = Δu |
die säkulare Aenderung der Temperatur der untersten Luftschicht veranschaulicht, so folgt aus (1l), (12) und (13)
| (14) |

|
d. h. wegen (6)
| (15) | Δu = 173,8 · ΔW. |
Will man die soeben gewonnene Formel benützen, um die säkularen Schwankungen der Mitteltemperatur des kalorischen Sommer- bzw. Winterhalbjahres zu berechnen, dann ist folgendes zu berücksichtigen.
In der Formel (15) ist für ΔW die pro Minute berechnete Bestrahlung der Flächeneinheit und zwar in Grammkalorien einzusetzen. Die in der Tabelle XXV mitgeteilten säkularen Schwankungen ΔQs und ΔQw der sommerlichen bzw. der winterlichen Strahlungsmengen Qs und Qw sind in kanonischen Einheiten ausgedrückt, für die J0 = 1; T = 100.000 gesetzt wurde. Weil das Jahr T = 525.942 Minuten umfasst und J0 = 1,946 Grammkalorien pro Minute beträgt, hat man, wie im § 85 auseinandergesetzt, die Zahlen der Tabelle XXV mit 1,946 · T ⁄ 100.000 zu multiplizieren und nachher, da das kalorische Halbjahr ½ T Minuten umfasst, mit dieser Zahl zu dividieren, also alles in allem mit 50.000 zu dividieren und mit 1,946 zu multiplizieren. Man bekommt also

|
d. h. abgerundet

|
Die vorstehenden Formeln besagen, dass man die in Celsiusgraden gemessenen säkularen Aenderungen der Mitteltemperaturen des kalorischen Sommer- bzw. Winterhalbjahres erhält, wenn man die in der Tabelle XXV enthaltenen Zahlen durch 150 dividiert.
Die Berechnung der säkularen Schwankung ΔuT der Mitteltemperatur uT des ganzen Jahres geschieht auf folgende Weise
| ΔQT = ΔQs + ΔQw |
gegeben. Weil das Jahr 100.000 kanonische Zeiteinheiten umfasst, so ergeben die vorstehenden Ueberlegungen
| (17) |

|
d. h., wie zu erwarten,
| ΔuT = ½ · (Δus + Δuw) |
§ 121. Die mittelbaren klimatischen Effekte des säkularen Ganges der Erdbestrahlung. Das vorstehend gewonnene Ergebnis gilt nur, wenn die bei der Ableitung desselben gemachten Voraussetzungen erfüllt sind, d. h. wenn das Reflexionsvermögen A unverändert bleibt. Dies ist der Fall solange das in Betracht gezogene Gebiet der Erdoberfläche nicht unter eine auch den Sommer überdauernde Eisdecke gelangt, d. h. nur für die während der Vorzeit nicht vereisten Gebiete. In den vereisten Gebieten kommt der mächtige Einfluss der Schneedecke zur Geltung. Durch eine solche Decke wird das Reflexionsvermögen A wesentlich vergrössert und ein namhafter Teil der auf dieses Gebiet während des Sommers auffallenden Strahlung wird für den Wärmehaushalt unbenützt in den Weltraum zurückgewiesen. Mit zunehmender Mächtigkeit der Schneedecke rückt die Oberfläche des Gebietes in die Höhe und es entspricht, wie noch gezeigt werden wird, jeder Erhebung dieser Oberfläche um 150 Meter eine Verminderung der mittleren Sommertemperatur von einem Grad Celsius. Kommt dann im Laufe der Zeit die säkulare Vergrösserung der sommerlichen Bestrahlung an die Reihe, so braucht es langer Zeiträume bis diese Bestrahlung thermisch zur Geltung kommt, denn ein grosser Bruchteil dieser, Bestrahlung muss vorerst zum Abschmelzen des angehäuften Schnees verwendet werden.
Ich habe in meiner "Mathematischen Klimalehre", § 42, eine mathematische Beschreibung der vorstehend geschilderten Erscheinungen geliefert, und Soergel hat sie praktisch verwertet, worüber hier kurz berichtet werden möge, wobei ich mich auch der bereits angeführten Monographie Soergels "Das Eiszeitalter" bediene.
Aus der Strahlungskurve lassen sich die Zeiten der maximalen bzw. minimalen sommerlichen und winterlichen Bestrahlungen der in Betracht gezogenen Gebiete direkt ablesen, sie lässt aber nicht ohne weiteres erkennen, in welchem Zeitpunkt die Eismassen jeweils ihre grösste Ausdehnung besassen und zwar aus folgendem Grunde.
Wenn bei sinkender Strahlung die Ausdehnung der Eismassen zunimmt, so werden diese wachsenden Eismassen selbst ein Faktor der Abkühlung, so dass das Abkühlungsmass und damit die Tendenz zur Eiserhaltung und Eisausdehnung über das Mass der Strahlungsminderung hinaus eine Steigerung erfährt. Mit sinkender Strahlung und wachsender Eisausdehnung werden die Bedingungen zur weiterer Vergrösserung des Eisschildes zunehmend günstiger. Als die Strahlung zur Zeit einer Kaltsommerperiode ihren tiefsten Stand erreichte, waren die Eismassen im Vormarsch, war ihre Kältewirkung noch in Wachsen. Als die Strahlung wieder zu steigern begann, blieb der geringe Wärmegewinn für lange Zeit gegenüber der Kältewirkung der Eismassen ohne entscheidenden Einfluss, weshalb sich der Eishochstand gegenüber dem Strahlungstief verzögerte, Soergel unternahm es mit Berücksichtigung der für das Abschmelzen des Eises erforderlichen Strahlungsmengen, diese Verzögerung abzuschätzen und auf Grund der geologischen Befunde, die sich vorwiegend auf das Gebiet zwischen dem elften und neunzehnten Grad östlicher Länge erstreckten, aus der Strahlungskurve eine Kurve zu konstruieren, die er die Vereisungskurve nannte und aus der ersichtlich ist, wo der Rand der nordischen Eismassen jeweils gelegen hat. Auf diese Weise liessen sich die zeitliche Stellung und Dauer nicht nur der Eiszeiten, sondern auch der Zwischeneiszeiten mit einer für die Aufgaben der Eiszeitforschung zunächst hinreichender Genauigkeit festlegen.
Aus der Soergelschen Vereisungskurve kann man auch die Dauer der Vorstossphase und der grossen Rückschmelzphase ablesen, es können aus der Strahlungs- und Vereisungskurve die Klima- bzw. Temperaturverhältnisse im jeweiligen Vor- und Umland des Eises abgeleitet werden.
In weiterer Anwendung der Strahlungs- und Vereisungskurve gelang es Soergel, Tier- und Pflanzenfunde, die körperlichen Reste der Menschen und ihre Kulturen ihrer absoluten Zeitstellung nach zu bestimmen. Auf diese Weise ergaben sich folgende das ungefähre Alter der Einzelfunde bezeichnende Zahlen: Homo Heidelbergensis etwa 530.000 Jahre vor der Gegenwart, der Urmensch von Steinheim, je nachdem die Kiese, aus denen der Schädel zu tage kam, vor die erste und die zweite Risseiszeit gehören, etwa 300.000 bzw. 200.000 vor heute, die Ehringsdorfer Neandertal-Rasse etwa 128.000 vor heute, der Neandertaler aus dem Neandertal bei Düsseldorf, nach dem Alter westeuropäischer, mit Säugetierresten und Steinwerkzeugen überlieferter Funde beurteilt, etwa 115.000-100.000 vor heute; der Schädel aus der Höhle am Vogelherd nach allgemeiner Alterstellung der begleitenden Steinwerkzeuge etwa 80.000 vor heute und die Skelette von Oberkasse1 bei Bonn auf Grund der mit ihnen gefundenen Knochenarbeiten etwa 60.000 vor heute.
Ich habe, wie im Vorwort berichtet, nach der Veröffentlichung der "Mathematischen Klimalehre" einen anderen Weg gefunden, den wichtigsten klimatischen Effekt des säkularen Ganges der Erdbestrahlung, die säkularen Verschiebungen der Schneegrenze, mathematisch zu erfassen und mit diesem Gange in direkte Beziehung zu bringen. Wie dies geschehen ist, soll nachstehend gezeigt werden.
§ 122. Die durch den säkularen Gang der Erdbestrahlung unmittelbar hervorgerufenen Verschiebungen der Schneegrenze.
§ 123. Klimatische Auswirkungen der säkularen Aenderungen des Reflexionsvermögens der Erde.
Kapitel XXIII
Mechanismus und Ablauf der grossen klimatischen Schwankungen des Quartärs
§ 124. Zusammenfassung der Ergebnisse über den säkularen Gang der Erdbestrahlung-und seine klimatischen Auswirkungen. Die vorstehenden Ergebnisse und namentlich jene der Tabellen XXV und XXVIII sollen jetzt zusammengefasst und überblickt werden.
Durch die zahlenreiche Tabelle XXV ist der säkulare Bestrahlungsgang der Erde während der letztverflossenen 600 Jahrtausende exakt dargestellt. Einen zusammenfassenden Ueberblick dieses Ganges würde wohl am besten eine graphische Darstellung der Ergebnisse dieser Tabelle ermöglichen, wie eine solche durch die Fig. 37 dieses Werkes zwecks Veranschaulichung des jährlichen Ganges der Erdbestrahlung zur Anwendung gekommen ist. Ein solches Graphikon würde den komplizierten säkularen Gang der Bestrahlung nicht nur der in der Tabelle XXV enthaltenen sechszehn geographischen Breiten, sondern der ganzen Erdoberfläche auf das augenscheinlichste zum Ausdruck bringen; ein nach demselben Prinzip hergestelltes dreidimensionales Modell würde einem solchen Zweck noch besser erfüllen.
Ein Graphikon von der vorstehend angegeben Art müsste in einem entsprechend grossen Massstabe ausgeführt werden, der das Blattformat dieses Buches weit überschreiten würde, weshalb ich mich hier damit begnügen muss, den säkularen Gang nur einiger ausgewählter Breiten graphisch zu veranschaulichen, Dies ist durch die beiliegende Fig. 55 geschehen, die ich meinen "Astronomischen Mitteln" entnehme.

In der Fig. 55 ist der säkulare Gang der sommerlichen Bestrahlung der Breiten von 15°, 45° und 75° nördlich und südlich zur Darstellung gebracht, wobei die säkularen Aenderungen des Reflexionsvermögens der Erde noch nicht berücksichtigt erscheinen. Man ersieht aus dieser Figur, dass, wie im Kapitel XV bereits festgestellt, der säkulare Bestrahlungsgang an den verschiedenen geographischen Breiten einen sehr verschiedenen Verlauf gehabt hat. Er war an den hohen Breiten der nördlichen und der südlichen Hemisphäre fast gleichverlaufend, an den tropischen Breiten war er entgegengesetzt, d. h. jener der tropischen Breiten der südlichen Hemisphäre ein Spiegelbild jenes der tropischen Breiten der nördlichen Hemisphäre; an den mittleren Breiten der beiden Hemisphären war er weder gleichverlaufend noch spiegelbildlich, sondern verschiedenartig. Dies rührt davon her, dass in den Formeln (1) und (2), die zur Berechnung dieses Ganges dienten, an den hohen Breiten wegen des grossen numerischen Wertes des Koefizienten ΔW, der Einfluss der Aenderungen Δε der Ekliptik ε sich besonders fühlbar macht, an den niederen Breiten dagegen wegen der überwiegenden Grösse des Koeffizienten m der Einfluss der durch den Ausdruck &916;(e · sin Πγ) dargestellten Aenderungen der beiden übrigen Elemente e und Πγ zur Geltung gelangt. Weil sich der Einfluss der Aenderungen des ersten der obigen drei Elemente auf beiden Hemisphären in demselben Sinne, der Einfluss der Aenderungen der übrigen zwei Elemente aber in entgegengesetzem fühlbar macht, ergeben sich daraus diese so deutlich zum Vorschein kommenden Eigenschaften des säkularen Bestrahlungsganges.
Dieser Bestrahlungsgang kam im klimatischen Bilde der Vorzeit vor allem dadurch zur Geltung, dass er gleichsinnige Aenderungen der jahreszeitlichen Mitteltemperaturen zeitigte, die man nach der Formel (16) erhält, wenn man die in der Tabelle XXV enthaltenen Zahlen durch 150 dividiert. Durch solche Aenderungen sank, wie aus der Fig. 55 sofort ersichtlich, die Mitteltemperatur des Sommerhalbjahres an den hohen und gemässigten Breiten der beiden Hemisphären mitunter um mehr als 5°, um wie wir sehen werden, die Ursache weiterer tiefgehender klimatischer Aenderungen zu werden. Aber auch in der tropischen~Zone, wo eine solche mittelbar hervorgerufene weitere Temperaturänderung entweder ganz unterblieb oder nur gering gewesen sein könnte, war der primäre thermische Effekt des säkularen Ganges der Bestrahlung dieser Zone ganz bedeutend. Man ersieht aus der Fig. 55 und der Tabelle XXV, dass an der südlichen Breite von 15° das sommeriiche Strahlungsdefizit mehrere Male den Betrag von 1.000 kanonischen Strahlungseinheiten überschritten und eine Erniedrigung der mittleren Temperatur der wärmeren Jahreshälfte von über 7° hervorgerufen hatte.
Der augenscheinlichste Effekt dieser säkularen Aenderungen der Sommertemperaturen waren aber die dadurch gezeitigten Verschiebungen der Schneegrenze. Es folgt aus der im § 122 abgeleiteten Korrelation zwischen der Aenderung der sommerlichen Bestrahlung und der zugehörigen Verschiebung der Schneegrenze, nach der jeder Aenderung der sommerlichen Strahlungsmenge von einer kanonischen Einheit eine Verschiebung der Schneegrenze von einem Meter entspricht, dass in Gebirge tragenden Gebieten der Erde als primärer Effekt des säkularen Bestrahlungsganges die Schneegrenze nach oben bzw. nach unten sich verschob, je nachdem die säkulare Schwankung der sommerlichen Bestrahlung eine positive oder eine negative gewesen war. Dieser primäre Effekt überschritt, wie aus der Fig. 55 ersichtlich, an den hohen und den gemässigten Breiten der nördlichen Hemisphäre mitunter der Betrag von 500 m; an der südlichen Henlisphöre war er noch grösser.
Wir haben gesehen, dass die soeben angeführte Korrelation zwischen der Aenderung der sommerlichen Bestrahlung und der Verschiebung der Schneegrenze nur für das Breiteintervall zwischen 30° und 90° streng richtig ist. Für die tropische Zone, für die eine quantitativ gleiche Korrelation nicht bewiesen erscheint, bleibt uns ein anderer Weg offen, um die dort stattgefundenen Verschiebungen der Schneegrenze zu ermitteln. Hat sich dort die mittlere Temperatur der wärmeren Jahreshälfte, wie vorstehend angegeben, um 7° erniedrigt, so müssten wir, um nach einer solchen Temperaturerniedrigung auf der Isotherme der unteren Grenze des ewigen Schnees zu verbleiben, um eine Strecke tiefer heruntersteigen, die man erhält, wenn man die obige Temperaturerniedrigung mit der Abnahme der Tenlperatur mit der Höhe multipliziert. Diese Abnahme ist für die einzelnen Gebirgsgegenden der tropischen Zone durch die Beobachtungen gegeben. Durch diese Feststellung wird die von einigen Geologen geäusserte Ansicht, der säkulare Bestrahlungsgang könne die in der tropischen Zone stattgefundenen Schneegrenzeverschiebungen nicht erklären, hinfällig.
Fragen wir nun nach den durch die obigen Verschiebungen der Höhenlage der Schneegrenze hervorgerufenen klimatischeu Auswirkungen! Diese sind zweifacher Art, je nachdem diese Verschiebungen der nichtarktischen oder der arktischen Zone angehören.
In der nichtarktischen Zone vergrösserte jede Verschiebung der Schneegrenze nach unten das Flächenausmass der Schneebedeckung der Gebirge tragenden Gebiete der Erde. Dies war beispielsweise in den Alpen der Fall. Sank dort die Schneegrenze nach unten, so kam dadurch ein weiterer Teil der Gegend unter eine auch den Sommer überdauernde Schneedecke. Wie gross diese Verbreiterung der Schneedecke gewesen ist, das hing von den Böschungsverhältnissen des Gebietes ab. Die Ermittlung dieser Vergrösserung des Flächenausmasses der Schneebedeckung und deren klimaiischer Auswirkung ist Gegenstand regionaler Erforschung. Solche Untersuchungen würden den festgelegten Rahmen meines Werkes überschreiten, weshalb ich auf sie verzichten muss. Ich kann mich zu einem solchen Verzicht um so leichter entschliessen, als ich in der Lage war, die anderen weitaus mächtigeren Auswirkungen der säkularen Aenderungen der Höhenlage der Schneegrenze, jene, die in den polaren Gegenden der Erde vor sich gegangen sind, in den Bereich meiner Untersuchungen einzubeziehen auf Grund folgender Ueberlegungen.
Betrachtet man das durch die Fig. 53 dargestellte Diagramm der gegenwärtigen Höhenlage der Schneegrenze, so ersieht man, dass diese Grenze in den nördlichen Gegenden der Erde an der Breite von etwa 75° die Oberfläche der Kontinentaltafeln erreicht. Bis zu dieser Breite reicht durchschnittlich die nördliche polare Schneekalotte der Erde. Sank diese Höhenlage der Schneegrenze, so wie es im Verlauf der Vorzeit mehrere Male gewesen ist, um etwa 500 m, so hat sie, wie aus der Fig. 53 sofort ersichtlich, die Oberfläche der Kontinente bereits an einer Breite von etwa 65° erreichen müssen, d. h. die polare Schneekalotte musste damals um rund 10° breiter gewesen sein als gegenwärtig und hatte, wie es eine einfache Ausrechnung ergibt, ein 2,75 Mal grösseres Ausmass. Durch eine solche Vergrösserung des Flächenausmasses der polaren Schneedecke veränderte sich das Reflexionsvermögen der Erde ganz empfindlich und ein namhafter Teil der auf diese schneebedeckten Gegenden der Erde auffallenden Sonnenstrahlung wurde auf Kosten des Wärmehaushaltes der Erde in den Weltraum zurückgewiesen. Weil das Reflexionsvermögen der Schneebedeckungen der Erde bald nach der Veröffentlichung meiner "Mathematischen Klimalehre" zuverlässig ermittelt wurde, kam ich bald in die Lage, die vorstehend geschilderte Erscheinung mathematisch zu erfassen, So ist es mir möglich gewesen, die Strahlungsverluste zu berechnen, die die Erde durch jede Vergrösserung ihrer polaren Schneekalotten im Laufe der Vorzeit erlitten hat. Dies ist im vorstehenden Paragraphen geschehen, worin die gewonnenen Ergebnisse der Rechnung durch die umfangreiche Tabelle XXVIII systematisch zusammengestellt sind.
Die ersten sieben Seiten dieser Tabelle enthalten die auf die beiden bis zu den Breiten von 55° reichenden polaren Kalotten der Erde sich beziehenden Rechnungsergebnisse. In der ersten Kolumne dieser Tabelle sind die einzelnen Zeitpunkte der geologischen Vorzeit, auf die sich die Berechnungen bezogen hatten, eingetragen; die zweite und die dritte Kolumne enthält die durch die Veränderungen der astronomischen Elemente hervorgerufenen säkularen Aenderungen Δ1Qw und Δ1Qs der pro Flächeneinheit berechneten winterlichen bzw. sommerlichen Bestrahlung der nördlichen Kalotte, die vierte Kolumne enthält die durch die Variabilität der Schneebedeckungen dieser Kalotte hervorgerufenen Aenderungen Δ2Qs der sommerlichen Bestrahlung dieser Kalotte. Die fünfte Kolumne enthält die totalen säkularen Aenderungen ΔQs = Δ1Qs + Δ2Qs der sommerlichen Bestrahlung der Kalotte.
Die durch die Veränderungen des Flächenausmasses der Schneebedeckungen hervorgerufenen Aenderungen Δ2Qw der winterlichen Bestrahlung habe ich nicht in den Bereich meiner Berechnungen einbezogen und zwar aus folgendem Grunde. Die in Betracht gezogenen Gegenden der Erde sind nämlich auch gegenwärtig während des grössten Teiles des Winterhalbjahres mit Schnee bedeckt. Während der grossen Kältevorstösse der Vorzeit war dies allerdings während des ganzen Winterhalbjahres der Fall gewesen, doch konnte selbst damals die Aenderung Δ2Qw nicht gross gewesen sein, um in der jährlichen Bestrahlungssumme eine Rolle zu spielen.
Die Kolumnen sechs bis neun der Tabelle XXVIII enthalten die auf die südliche Kalotte der Erde sich beziehenden Aenderungen Δ1Qw, Δ1Qs und Δ2Qs. Die restlichen Seiten der Tabelle beziehen sich auf den säkularen Gang der bis zur Breite von 45° bzw. 30° reichenden nördlichen und südlichen Kalotten der Erde.
Die wichtigsten Resultate der Tabelle XXVIII sind, um sie überblicken und hier besprechen zu können, in der beiliegenden Fig. 56 graphisch veranschaulicht.

Die oberste Kurve der Fig. 56 stellt den mit Berücksichtigung der Aenderungen des Reflexionsvermögens der Erde sich ergebenden säkularen Bestrahlungsgang der sommerlichen Bestrahlung der nördlichen bis zur Breite von 55° reichenden Kalotte der Erde dar. Die Ordinaten dieser Kurve geben also die jeweiligen totalen Variationen ΔQs = Δ1Qs + Δ2Qs der pro Flächeneinheit berechneten sommerlichen Bestrahlung an. Wie aus der Figur ersichtlich, erreichten die negativen Ausschläge dieser Grösse während der Vorzeit mehrere Male sehr hohe Beträge. Zur Zeit von 230 Jahrtausenden vor der Gegenwart betrug dieser Fehlbetrag der sommerlichen Strahlungsmenge 2180 kanonische Strahlungseinheiten. Diesem Betrag entsprach eine Verschiebung der Schneegrenze nach unten von 2.180 m. Nach der letzten Kolumne der Tabelle XXVII beträgt die gegenwärtige Höhenlage der solaren Schneegrenze an der Breite von 55° 2.256 m. Weil sie sich zu jener Zeit um den soeben angegebenen Betrag nach unten zu verschob, hat sie die Oberfläche der Kontinentaltafeln erreichen müssen, so dass damals die nördliche polare Schneebedeckung der Erde bis zur Breite von 55° reichen musste, wie es tatsächlich der Fall gewesen ist.
Die positiven Ausschläge der Grösse ΔQs waren während der Vorzeit nicht unbedeutend kleiner als die negativen. Dies ist leicht verständlich. Jede Verbreiterung der polaren Schneedecke der Erde brachte wegen der ständigen Zunahme des Umfangs der Breitekreise gegen den Aequator zu immer längere ringf 6#246;rmige Streifen der Erdoberfläche unter die Schneehaube, so dass ihre reflektierende Fläche mit dem Quadrat der Poldistanz zunahm. Bei einer Zusammenschrumpfung der Schneedecke nahm ihre abkühlende Wirkung mit der Annäherung an den Pol rasch ab. Schmolz die polare Schneekalotte ganz ab, dann ward Δ2Qs gleich Null, und die positive Wirkung der Aenderung dzs Reflexionsvermögens der Erde erlosch vollständig.
Die unterste Kurve der Fig. 56 stellt den säkularen Gang der sommerlichen Bestrahlung der südlichen bis zur Breite von 55° reichenden Kalotte der Erde dar. Die Ausschläge dieser Kurve, die positiven und noch mehr die negativen, sind kleiner als jene der auf die nördliche Kalotte sich beziehenden Strahlungskurve. Dies rührt, wie bereits gesagt, davon her, dass sich das Ausmass der südlichen polaren Schneedecke der Erde während der Vorzeit weniger verändern konnte, weil ihre Verbreiterung auf Kosten des Meeres vor sich ging, ihrer Zusammenschrumpfung die grosse Höhe des antarktischen Kontinents entgegenwirkte. Auch waren die negativen Ausschläge dieser Strahlungskurve gleichmässiger; sie erreichten und überschritten manchmal den Betrag von 1.000 Strahlungseinheiten oder 1000 m Schneegrenzeverschiebung.
Wie aus den vorstehenden Daten ersichtlich, waren die beiden bis zu den Breiten von 55° reichenden Kalotten der Erde infolge der Veränderlichkeit der astronomischen Elemente und des Reflexionsvermögens dieser Kalotten starken Schwankungen der sommerlichen Strahlungsmengen unterworfen. Infolgedessen sank die solare mittlere Temperatur der wärmeren Jahreshälfte um Beträge, die auf der nördlichen Hemisphäre bis 14°, auf der südlichen bis 8° heranreichten. Zu diesen Zeiten sank auch die mittlere jährliche Temperatur ganz erheblich. Im 230 Jahrtausend vor der Gegenwart betrug, wie aus der Tabelle XXVIII mittels der Formel (17) abzuleiten, die säkulare Schwankung der jährlichen Strahlungsmenge -1.920 kanonische Einheiten und die zugehörige Verminderung der Jahrestemperatur -6,4°.
Die hie und da geäusserte Meinung, der säkulare Bestrahlungsgang könne keine bemerkbaren Schwankungen der Jahrestemperatur hervorrufen, ist, wie das vorstehende Rechnungsergebnis zeigt, unbegründet und unhaltbar.
Die grossen säkularen Temperaturänderungen, die auf den beiden vorstehend in Betracht gezogenen Kalotten der Erde während der Vorzeit stattfanden, haben sich durch Vermittlung der Luft- und Meeresströmungen auch ausserhalb dieser Kalotten fühlbar gemacht. Um über diese Auswirkung Auskunft zu erhalten, habe ich, wie aus der Tabelle XXVIII ersichtlich, den säkularen Gang der Bestrahlung der bis zu den Breiten von 45° bzw, 30° reichenden Kalotten berechnet und die wichtigsten Ergebnisse dieser Berechnung in der Fig. 56 ebenfalls graphisch veranschaulicht.
In der Fig. 56 stellt die zweite von oben gezählte Strahlungskurve den mit Berücksichtigung der ermittelten Aenderungen des Reflexionsvermögens der Erde sich ergebenden pro Flächeneinheit berechneten säkularen Gang der sommerlichen Bestrahlung der nördlichen bis zur Breite von 45° reichenden Kalotte der Erde dar. Die zweite Strahlungskurve von unten bezieht sich auf die süfliche bis zur Breite von 45° südlich reichende Kalotte; die beiden mittleren Strahlungskurven beziehen sich auf die beiden bis zur Breite von 30° reichenden Kalotten. Wie aus diesen Kurven ersichtlich, waren die in den polaren Gegenden der Erde während der Vorzeit durch die dort abgelagerten Schneemassen erfolgten Strahlungsverluste gross genug, um selbst den durchschnittlichen Bestrahlungszustand der bis zu den Breiten von 30° reichenden Kalotten mächtig zu beeinflussen und sich dadurch in allen aussertropischen Gebieten der Erde deutlich fühlbar zu machen.
§ 125. Zeitliche Abfolge und Ausmass der grossen klimatichen Schwankungen der letztverflossenen 660 Jahrtausende.
§ 126. Die vor dem 600. Jahrtausend stattgefundenen klimatischen Schwankungen.
§ 127. Einzelheiten über den Verlauf der klimatischen Schwankungen des Eiszeitalters.
Quelle: Milutin Milanković, Kanon der Erdbestrahlung und seine Anwendung auf das Eiszeitproblem. Éditions Speciales Tome CXXXIII. Acadédemie Royale Sebe. Belgrade 1942.
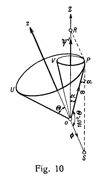
Herr Milankovitch nähert sich dem Problem der wiederkehrenden Eiszeiten mit klassischer Mechanik. Mit dem Gravitationsgesetz analysiert er die Zwei-Körper-Probleme Sonne-Erde und Erde-Mond und erstellt Vektorgleichungen für die Drehbewegungen. Damit erhält er Ausdrücke für die Präzession und die Nutation der Erdachse. Diese Betrachtungen gelten streng nur für punktförmige Massen.
Inzwischen hatte Alfred Wegener die Kontinentaldrifttheorie entwickelt, nach der die Erdoberfläche aus Schollen besteht, die auf einem flüssigen Erdkern schwimmen. Und da die Erde eine Kugel ist und kein Punkt, muss die Verteilung der Massen auf ihrer Oberfläche einen Einfluss auf ihren Drehimpuls haben. Und da eine Änderung des Drehimpulses ein Drehmoment senkrecht zur Richtung des Drehimpulses bewirkt, wird die Erdachse gekippt: die Schiefe der Ekliptik verändert sich. Damit hatte die Erklärung der Eiszeiten von James Croll in ihrem wesentlichen Punkt ergänzt und dessen Schlußfolgerung widerlegt.
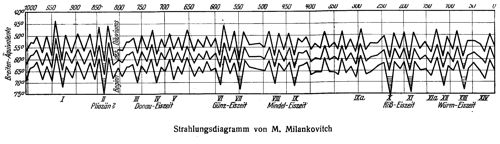
Milankovitć schätzt nun anhand der geologisch nachweisbaren Vereisungen die Zeitparameter der unterschiedlichen Drehbewegungen ab und erhält die Zyklen der Vereisungen durch die Einstrahlung der Sonnenenergie auf den Polregionen der Erde: die Milankovitć-Zyklen, die den Wechsel zwischen Eiszeit und Warmzeit qualitativ beschreiben. Die Neigung der Erdachse zur Ekliptik ändert sich innerhalb von ca. 41.000 Jahren zwischen 22,2° und 24,5°.
Ursache für die Veränderung der Neigung der Erdachse zur Ekliptik könnte die unterschiedliche Rotationsgeschwindigkeit von Erdmantel und innerstem Kern sein, die von Yi Yang und Xiaodong Song beobachtet worden ist. Bei einem Kreisel hängt der Drehimpuls von der Rotationsgeschwindigkeit ab, und eine Änderung verursacht ein Drehmoment, das die Rotationsachse kippt.
In den Naturwissenschaften muss eine gültige Theorie alle Beobachtungen berücksichtigen und experimentell überprüfbare Vorhersagen machen. Wie eine Untersuchung eines Eisbohrkerns in der östlichen Antarktis zeigte, sind die Milankovitć-Zyklen tatsächlich nachweisbar. Eine internationale Forschergruppe um den Paläoklimatologen Jean-Robert Petit konnte über einen Zeitraum vom 420.000 Jahren nachweisen, dass die Klimaschwankungen mit vorhergesagten Perioden vorkommen. Darüber hinaus stellten sie fest, dass Klimaerwärmungen im Beobachtungszeitraum mit Anstiegen der Konzentration von CO2 und CH4 einhergingen.
Quelle: J. R. Petit et al.: Climate and atmospheric history of the past 420,000 years from the Vostok ice core, Antarctica. Nature, Vol 399, 3 June 1999, S. 429 ff.
J. R. Petit et al.: Climate and atmospheric history of the past 420,000 years from the Vostok ice core, Antarctica. Nature, Vol 399, 3 June 1999, S. 429 ff.
Die andere Theorie zur Klimaerwärmung beruht auf der Freisetzung von Kohlendioxid (CO2) durch die Verbrennung fossiler Brennstoffe. Der Anstieg der Treibhausgase (CO2 und CH4) soll Wärme in der Atmosphäre binden und so die Temperatur der Erdatmosphäre erhöhen (Treibhauseffekt). Nun gehört die Wärmekapazität zu den kolligativen Eigenschaften von Gasen. Mir ist aber nicht verständlich, warum die Diskussion auf das Kohlendioxid fokussiert ist: die Wärmekapazität des CO2 ist mit 0,846 kJ·kg-1·K-1 geringer als die der trockenen Luft mit 1,016 kJ·kg-1·K-1. Wasserdampf dagegen hat eine spezifische Wärme von 2,086 kJ·kg-1·K-1. Eine so rigorose wissenschaftliche Theorie wie die von Milankovitć habe ich nicht gefunden.
Allerdings publizierte Svante Arrhenius im Philosophical Magazine and Journal of Science einen Beitrag mit dem Titel "On the Influence of Carbonic Acid in the Air upon the Temperature of the Ground ". Darin untersucht er, ob die Eiszeiten des Tertiär durch Abnahme des Kohlendioxids in der Atmosphäre hervorgerufen worden sind, z. B. durch die Bildung der mächtigen Kalksteinschichten oder durch Bindung in Pflanzen, die dann zu Kohlelagerstätten wurden (Theorie von Arvid Gustaf Högbom). Er analysiert Messungen verschiedener Autoren und interpoliert die Werte der Sonnenenstrahlung bzw. Abstrahlung (Albedo) für verschiedene geographische Breiten und Jahreszeiten. Mir erscheint, er beschreibt (1896!) die Modelle der heutigen Meteorologen und Arrhenius kommt - wen wundert es - zu einem ähnlichen Ergebnis.
Wir haben nun zwei Hypothesen zur Entstehung von Eiszeiten: die astronomische und die Kohlendioxidtheorie. Es gibt nur mehr oder weniger polemische Diskussionsbeiträge wie den von Michael Schmitt oder Behauptungen wie die des Umweltbundesamtes. Hilfreich für eine Erkenntnis sind beide nicht. Immerhin wird die astronomische Ursache des Klimawandels mindestens von der Helmholtz Klima Initiative in das Kalkül einbezogen.
[Wärmeabsorption] [Strahlungsabsorption] [CO2 Einluss]
© Rainer Stumpe, URL: www.rainerstumpe.de/
Datenschutzerklärung



























