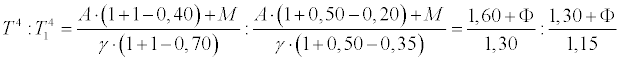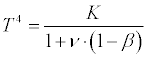[Wärmeabsorption] [Strahlungsabsorption] [CO2 Einfluss]
The London, Edinburgh, And Dublin
PHILOSOPHICAL MAGAZINE
AND
JOURNAL OF SCIENCE.
APRIL 1896
XXXI. On the Influence of Carbonic Acid in the Air upon the Temperature of the Ground.
By Svante Arrhenius.
I. Introduction: Observations of Langley on Atmospheric Absorption.
A great deal has been written on the influence of the absorption of the atmosphere upon the climate. [John] Tyndall in particular has pointed out the enormous importance of this question. To him it was chiefly the diurnal and annual variation of the temperature that were lessened by this circumstance. Another side of the question, that has long attracted the attention of physicists, is this: Is the mean temperature of the ground in any way influenced by the presence of heat-absorbing gases in the atmosphere? [Jean Baptiste Joseph] Fourier maintained that the atmosphere acts like the glass of a hothouse, because it lets through the light rays of the sun but retains the dark rays from the ground. This idea was elaborated by [Claude Servais Mathias] Pouillet; and [Samuel Pierpont] Langley was by some of his researches led to the view, that "the temperature of the earth under direct sunshine, even though our atmosphere were present as now, would probably fall to -220° C., if that atmosphere did not possess the quality of selective absorption". This view, which was founded on too wide a use of Newtons law of cooling, must be abandoned, as Langley himself in a later memoir showed that the full moon, which certainly does not possess any sensible heat-absorbing atmosphere, has a "mean effective temperature" of about 45° C.
The air retains heat (light or dark) in two different ways. On the one hand, the heat suffers a selective diffusion on its passage through the air; on the other hand, some of the atmospheric gases absorb considerable quantities of heat. These two actions are very different. The selective diffusion is extraordinarily great for the ultra-violet rays, and diminishes continuously with increasing wave-length of the light, so that it is insensible for the rays that form the chief part of the radiation from a body of the mean temperature of the earth.
The selective absorption of the atmosphere is, according to the researches of Tyndall, Lecher and Pernter, Röntgen, Heine, Langley, Ångström, Paschen, and others, of a wholly different kind. It is not exerted by the chief mass of the air, but in a high degree by aqueous vapour and carbonic acid, which are present in the air in small quantities. Further, this absorption is not continuous over the whole spectrum, but nearly insensible in the light part of it, and chiefly limited to the long-waved part, where it manifests itself in very well-defined absorption-bands, which fall off rapidly on both sides. The influence of this absorption is comparatively small on the heat from the sun, but must be of great importance in the transmission of rays from the earth. Tyndall held the opinion that the water-vapour has the greatest influence, whilst other authors, for instance Lecher and Pernter, are inclined to think that the carbonic acid plays the more important part. The researches of Paschen show that these gases are both very effective, so that probably sometimes the one, sometimes the other, may have the greater effect according to the circumstances.
In order to get an idea of how strongly the radiation of the earth (or any other body of the temperature +15° C.) is absorbed by quantities of water-vapour or carbonic acid in the proportions in which these gases are present in our atmosphere, one should, strictly speaking, arrange experiments on the absorption of heat from a body at 15° by means of appropriate quantities of both gases. But such experiments have not made as yet, and, they would require very expensive apparatus beyond that at my disposal, I have not been in a position to execute them. Fortunately there are other researches by Langley in his work on "The temperature of the Moon," with the aid of which it seems not impossible to determine the absorption of heat by aqueous vapour and by carbonic acid in precisely the conditions which occur in our atmosphere. He has measured the radiation of the full moon {if the moon was not full, the necessary correction relative to this point was applied) at different heights and seasons of the year. This radiation was moreover dispersed in a spectrum, so that in his memoir we find the figures for the radiant heat from the moon for 21 different groups of rays, which are defined by the angle of deviation with a rocksalt prism having a refracting angle of 60 degrees. The groups lie between the angles 40° and 35°, and each group is separated from its neighbours by an interval of 15 minutes. Now the temperature of the moon is nearly the same as that of the earth, and the moon-rays have, as they arrive at the measuring-instruments, passed through layers of carbonic acid and of aqueous vapour of different thickness according to the height of the moon and the humidity of the air. If, then, these observations were wholly comparable with one another, three of them would suffice for calculating the absorption coefficient relatively to aqueous vapours and carbonic acid for any one of the 21 different groups of rays. But, as an inspection of the 24 different series of observations will readily show, this is not the case. The intensity of radiation for any group of rays should always diminish with increasing quantity of aqueous vapour or carbonic acid traversed. Now the quantity of carbonic acid is proportional to the path of the ray through the atmosphere, that is, to the quantity called "Air-mass" in Langley's figures. As unit for the carbonic acid we therefore take air-mass = 1, i. e. the quantity of carbonic acid that is traversed in the air by a vertical ray. The quantity of aqueous vapour traversed is proportional partly to the "air-mass," partly to the humidity, expressed in grammes of water per cubic metre. As unit for the aqueous vapour I have taken the quantity of aqueous vapour that is traversed by a vertical ray, if the air contains 10 grammmes per cubic metre at the earth's surface. If we tabulate the 24 series of observations published by Langley in the work cited with respect to the quantities of carbonic acid and aqueous vapour, we immediately detect that his figures run very irregularly, so that very many exceptions are found to the rule that the transmitted heat should continuously decrease when both these quantities increase.
And it seems as if period of alterations with the time of observation occurred in his series. On what circumstance these alterations with the time depend one can only make vague conjecture: probably the clearness of the sky may have altered within a long period of observation, although this could not be detected by the eye. In order to eliminate this irregular variation, I have divided the observations into four groups, for which the mean quantities of carbonic acid (K) and of water-vapour (W) were 1.21 and 0.36, 2.21 and 0.86, 1.33 and 1.18, and 2.22 and 2.34 respectively. With the help of the mean values of the heat-radiation for every group of rays in these four groups of observations, I have roughly calculated the absorption coefficients (x and y) for both gases, and by means of these reduced the value for each observation to the value that it would have possessed if K and W had been 1.5 and 0.88 respectively. The 21 values for the different rays were then summed up, so that I obtained the total heat-radiation for every series of observations, reduced to K = 1.5 and W = 0.88. If the materials of observation were very regular, the figures for this total radiation should not differ very much from one another. In fact, one sees that observations that are made at nearly the same time give also nearly equal values, but if the observations were made at very different times, the values differ also generally very much. For the following periods I have found the corresponding mean values of the total radiation:
| Period. | Mean value | Reduction factor |
| 1885, Feb. 21 - June 24 | 4850 | 1.3 |
| 1885, July 29 - 1886, Feb. 26 | 6344 | 1.00 |
| 1886, Sept. 13 - Sept. 18 | 2748 | 2.31 |
| 1886, Oct. 11 - Nov. 8 | 5535 | 1.15 |
| 1887, Jan. 8 - Feb. 9 | 3725 | 1.70 |
In order to reduce the figures of Langley to comparability with one another, I have applied the reduction factors tabulated above to the observations made in the respective periods. I have convinced myself that by this mode of working no systematic error is introduced into the following calculations.
After this had been done, I rearranged the figures of Langley's groups according to the values of K and W in the following table. (For further details see my original memoir.)
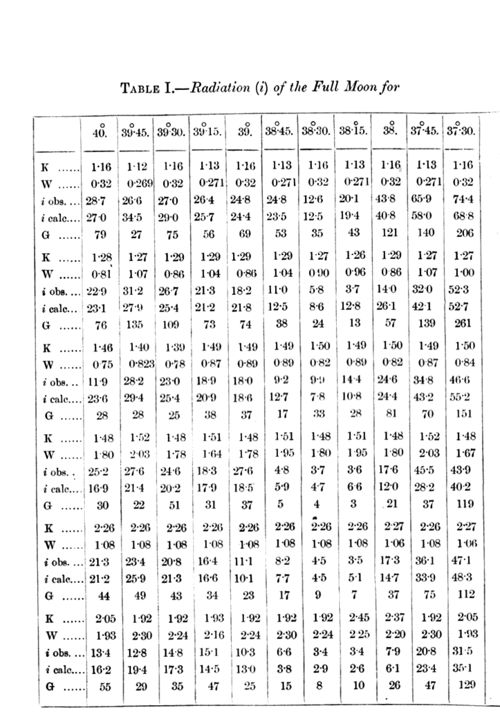
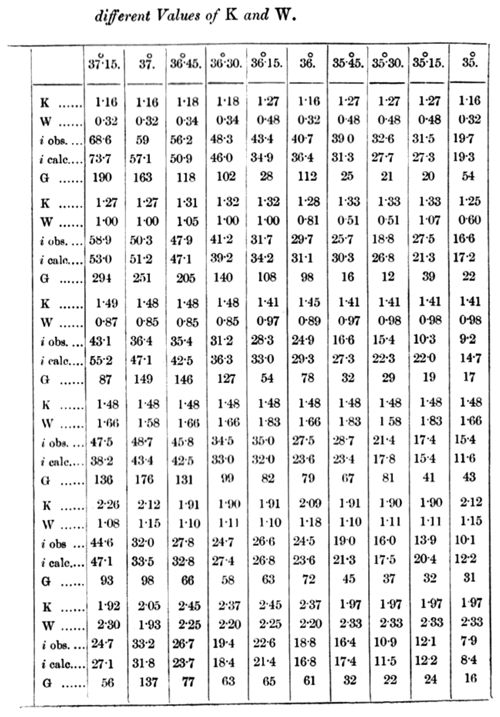
In this table the angle of deviation is taken as head-title. After K and W stand the quantities of carbonic acid and water-vapour traversed by the ray in the above-mentioned units. Under this comes after i obs. the intensity of radiation (reduced) observed by Langley on the bolometer, and after this the corresponding value i calc., calculated by means of the absorption-coefficient given in Table II. below. G is the "weight" given to the corresponding i obs. in the calculation, using the method of least squares.
For the absorption-coefficients, calculated in this manner, I give the following table. (The common logarithms of the absorption-coefficients are tabulated.)
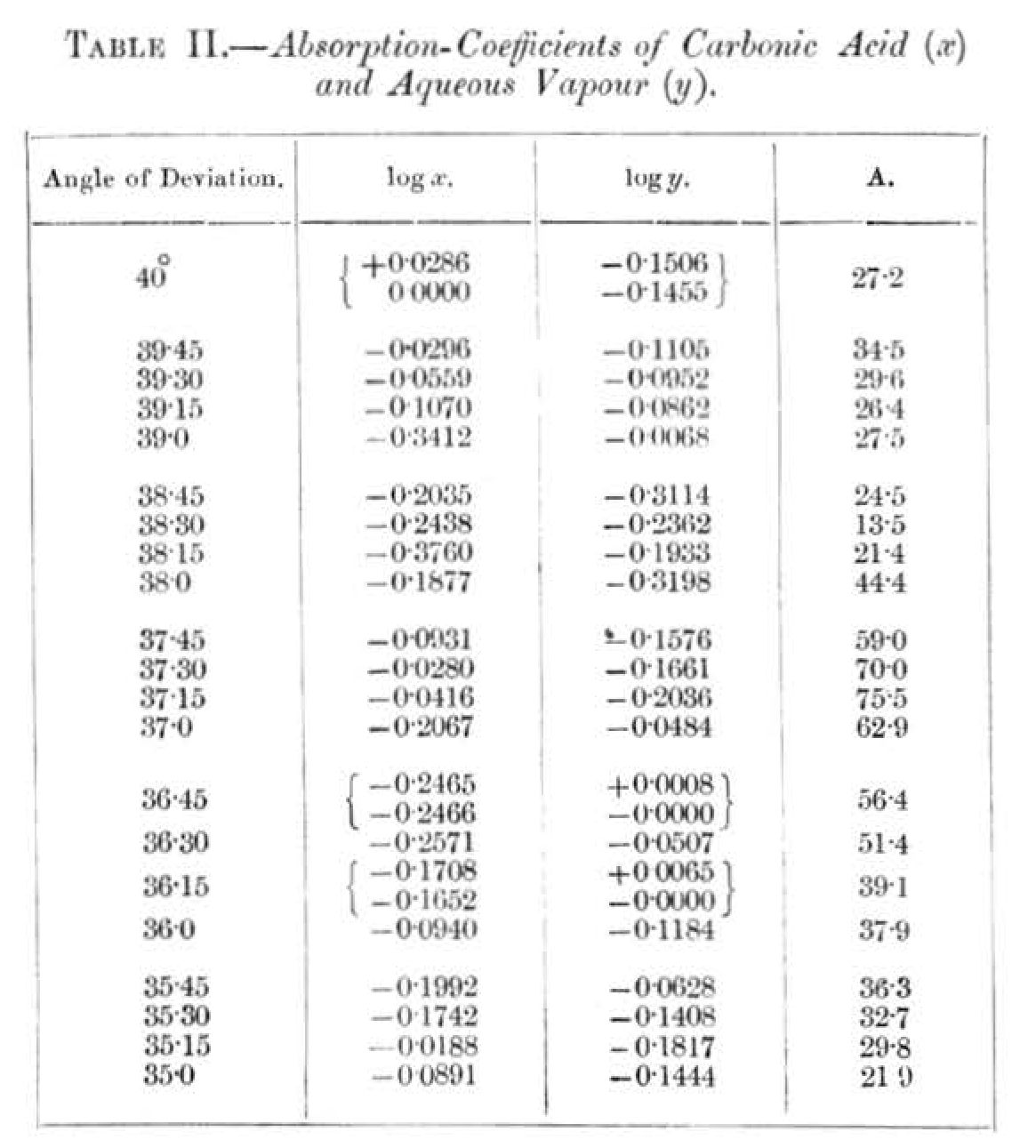
The signification of these figures may be illustrated by an example. If a ray of heat, corresponding to the angle of deviation 39° 45, passes through the unit of carbonic acid, it decreases in intensity in the proportion 1:0.934 (log = - 0.0296), the corresponding value for the unit or water-vapour is 1 : 0.775 (log = - 0.115). These figures are of course only valid for the circumstances in which the observations were made, viz., that the ray should have traversed a quantity of carbonic acid K = l.1 and a quantity of water-vapour W = 0.3 before the absorption in the next quantities of carbonic acid and water-vapour was observed. And these second quantities should not exceed K = 1.l and W = l.8, for the observations are not extended over a greater interval than between K = 1.1 and K = 2.2, and W = 0.3 and W = 2.1 (the numbers for K and W are a little different for rays of different kind). Below A is written the relative value of the intensity of radiation for a given kind of ray in the moonlight after it has traversed K = 1 and W = 0.3. In some cases the calculation gives positive values for log xor log y. As this is a physical absurdity (it would signify that the ray should be strengthened by its passage through the absorbing gas), I have in these cases, which must depend on errors of observation, assumed the absorption equal to zero for the corresponding gas, and by means of this value calculated the absorption-coefficient of the other gas, and thereafter also A.
As will be seen from an inspection of Table I., the values of i obs. agree in most cases pretty well with the calculated values i calc. But in some cases the agreement is not so good as one could wish. These cases are mostly characterized by a small "weight" G, that is in other words, the material of observation is in these cases relatively insufficient. These cases occur also chiefly for such rays as are strongly absorbed by water-vapour. This effect is probably owing to the circumstance that the aqueous vapour in the atmosphere, which is assumed to have varied proportionally to the humidity at the earth's surface, has not always had the assumed ideal and uniform distribution with the height. From observations made during balloon voyages, we know also that the distribution of the aqueous vapour may be very irregular, and different from the mean ideal distribution. It is also a marked feature that in some groups, for instance the third, nearly all the observed numbers are less than the calculated ones, while in other groups, for instance the fourth, the contrary is the case. This circumstance shows that the division of the statistic material is carried a little too far; and a combination of these two groups would have shown a close agreement between the calculated and the observed figures. As, however, such a combination is without influence on the correctness of the calculated absorption-coefficients, I have omitted a rearrangement of the figures in greater groups with consequent recalculation.
A circumstance that argues very greatly in favour of the opinion that the absorption-coefficient given in Table II. cannot contain great errors, is that so very few logarithms have a positive value. If the observations of Langley had been wholly insufficient, one would have expected to find nearly as many positive as negative logarithms. Now there are only three such cases, viz., for carbonic acid at an angle of 40°, and for water-vapour at the angles 36° 45 and 36° 15. The observations for 40° are not very accurate, because they were of little interest to Langley the corresponding rays not belonging to the moon's spectrum but only to the diffused sunlight from the moon. As these rays also do not occur to any sensible degree in the heat from a body of 15° C., this non-agreement is without importance for our problem. The two positive values for the logarithms belonging to aqueous vapour are quite insignificant. They correspond only to errors of 0.2 and 1.5 per cent. for the absorption of the quantity W = 1, and fall wholly in the range of experimental errors.
It is certainly not devoid of interest to compare these absorption-coefficients with the results of the direct observation by Paschen and Ångström. In making this comparison, we must bear in mind that an exact agreement cannot be expected, for the signification of the above coefficients is rather unlike that of the coefficients that are or may be calculated from the observation of these two authors. The above coefficients give the rate of absorptions of a ray that has traversed quantities of carbonic acid (K = 1.1) and water-vapour (W = 0.3); whilst the coefficients of Paschen and Ångström represent the absorption experienced by a ray on the passage through the first layers of these gases. In some cases we may expect a great difference between these two quantities, so that only a general agreement can be looked for.
According to Paschen's figures there seems to exist no sensible emission or absorption by the aqueous vapour at wave-lengths between 0.9μ. and 1.2μ. (corresponding to the angle of deviation 40°). On the other hand, the representation of the sun's spectrum by Langley shows a great many strong absorption-bands in this interval, among which those marked ρ, σ, τ, and ϕ are the most prominent, and these absorption-bands belong most probably to the aqueous vapour, That Paschen has not observed any emission by water-vapour in this interval may very well be accounted for by the fact that his heat-spectrum had a very small intensity for these short-waved rays. But it may be conceded that the absorption-coefficient for aqueous vapour at this angle in Table II. Is not very accurate (probably too great), in consequence of the little importance that Langley attached to the corresponding observations. After this occurs in Langley's spectrum the great absorption-band ψ at the angle 39,45 (λ = 1.4μ), where in Paschen's curve the emission first becomes sensible (log y = - 0,1105 in Table II). At wave-lengths of greater value we find according to Paschen strong absorption-bands at λ = 1.3μ (ι in Langley's spectrum), i. e. in the neighbourhood of 39° 30 and at λ = 2.64μ (Langley's Χ) a little above the angle 39° 15. In accordance with this I have found rather large absorption-coefficients for aqueous vapour at these angles (log y = - 0.0952 and - 0.862 resp.). From λ = 3.0μ to λ = 1.7μ. thereafter, according to Paschen the absorption is very small, in agreement with my calculation (log y= - 0.0068 at 39°, corresponding to λ = 4.3μ). From this point the absorption increases again and presents new maxima at λ = 5.5μ, λ = 6.6μ, and λ = 7.7μ, i. e., in the vicinity of the angles 38° 45 (λ = 5.5μ) and 38° 30 (λ = 7.1μ). In this region the absorption of the water-vapour is continuous over the whole interval, in consequence of which the great absorption-coefficient in this part (log y = - 0.3114 and - 0.2362) becomes intellible. In consequence of the decreasing intensity of the emission-spectrum of aqueous vapour in Paschen's curve we cannot pursue the details of it closely, but it seems as if the emission of the water-vapour would also be considerable at λ = 8.7μ (39° 15). Which corresponds with the great absorption-coefficient (log y = - 0.1933) at this place. The observations of Paschen are not extended further, ending at λ = 9.5μ, which corresponds to an angle of 38° 08.
For carbonic acid we find at first the value zero at 40°, in agreement with the figures of Paschen and Ångström. The absorption of carbonic acid first assumes a sensible value at λ = 1.5μ, after which it increases rapidly to a maximum at λ = 2.6μ, and attains a new extraordinarily strong maximum at λ = 4.6 μ (Langley's Y). According to Ångström the absorption of carbonic acid is zero at λ = 0.9μ, and very weak at λ = 1.69μ, after which it increases continuously to λ = 4.6μ and decreases again to λ = 6.0μ. This behaviour is entirely in agreement with the values of log x in Table II. From the value zero at 40° (λ = 1.0μ) it attains a sensible value (- 0·0296) at 39°·45 (λ = 1.4μ), and thereafter greater and greater values (- 0.0559 at 39° 30, and - 0.1070 at 39° 15) till it reaches a considerable maximum (- 0.3412 at 39°, λ = 4.3 μ). After this point the absorption decreases (at 38° 45 = 5.6μ, log y = - 0.2035). According to Table II. The absorption of carbonic acid at 38° 30 and 38° 15 (λ = 7.1μ and 8.7 μ) has very great values (log x = - 0.2438 and - 0.3730), whilst according to Ångström it should be insensible. This behaviour may be connected with the fact that Ångström's spectrum had a very small intensity for the larger wavelengths. In Paschen's curve there are traces of a continuous absorption by the carbonic acid in this whole region with weak maxima at λ = 5.2μ, λ = 5.9μ, λ = 6.6μ (possibly due to traces of water-vapour), λ = 8.4μ, and λ = 8.9μ. In consequence of the strong absorption of water-vapour in this region of the spectrum, the intensity of radiation was very small in Langley's observations, so that the calculated absorption-coefficients are there not very exact (cf. above, pp. 242 - 243). Possibly the calculated absorption of the carbonic acid may have come out too great, and that of the water-vapour too small in this part (between 38° 30 and 38° 0). This can happen the more easily, as in Table I. K and W in general increase together because they are both proportional to the "air-mass." It may be pointed out that this also occurs in the problems that are treated below, so that the error from this cause is not of so great importance as one might think at the first view.
For angles greater than 38° (λ > 9.5 μ.) we possess no direct observations of the emission or absorption of the two gases. The sun's spectrum, according to Langley, exhibits very great absorption-bands at about 37° 50, 37° 25, 37°, and 36° 40°. According to my calculations the aqueous vapour has its greatest absorbing power in the spectrum from 38° to 35° at angles between 37° 15 and 37° 45 (the figures for 35° 45, 35° 30, and 35° l5 are very uncertain, as they depend upon very few measurements), and the carbonic acid between 36° 30 and 37° 0. This seems to indicate that the first two absorption-bands are due to the action of water-vapour, the last two to that of carbonic acid. It should be emphasized that Langley has applied the greatest diligence in the measurement of the intensity of the moon's radiation at angles between 36° and 38°, where this radiation possesses its maximum intensity. It may, therefore, be assumed that the calculated absorption-coefficients for this part of the spectrum are the most exact. This is of great importance for the following calculations, for the radiation from the earth has by far the greatest intensity (about two thirds, cf. p. 250) in this portion of the spectrum.
II. The Total Absorption by Atmosphere of Varying Composition.
As we have now determined, in the manner described, the values of the absorption-coefficients for all kinds of rays, it will with the help of Langley's figures be possible to calculate the fraction of the heat from a body at 15° C. (the earth) which is absorbed by an atmosphere that contains specified quantities of carbonic acid and water-vapour. To begin with, we will execute this calculation with the values K = 1 and W = 0.3. We take that kind of ray for which the best determinations have been made by Langley, and this lies in the midst of the most important part of the radiation (37°). For this pencil of rays we find the intensity of radiation at K = l and W = 0.3 equal to 62.9; and with the help of the absorption-coefficients we calculate the intensity for K = O and W = 0, and find it equal to 105. Then we use Langley's experiments on the spectral distribution of the radiation from a body of 15° C, and calculate the intensity for all other angles of deviation. These intensities are given under the heading M. After this we have to calculate the values for K = l and W = 0.3. For the angle 37° we know it to be 62.9. For any other angle we could take the values A from Table II. 1f the moon were a body of 15° C. But a calculation of the figure of Very shows that the full moon has a higher temperature, about 100° C. Now the spectral distribution is nearly, but not quite, the same for the heat from a body of 15° C. and for that from one of 100° C. With the help of Langley's figures it is, however, easy to reduce the intensities for the hot body at 100° (the moon) to be valid for a body at 15° (the earth) The values of A reduced in this manner are tabulated below under the heading N.
| Angle | 40° | 39° 45 | 39° 30 | 39° 15 | 39° 0 | 38° 45 | 38° 30 | 38° l5 | 38° 0 | 37° 45 | 37° 30 |
| M | 3.4 | 11.6 | 24.8 | 45.9 | 84.0 | 121.7 | 161 | 189 | 210 | 210 | 188 |
| N | 3.l | 10.1 | 11.3 | 13.7 | 18.0 | 18.l | 11.2 | 19.6 | 41.4 | 59 | 70 |
| Angle | 37° 15 | 37° 0 | 36° 45 | 36° 30 | 36° 15 | 36° 0 | ° 45 | ° 30 | 35° 15 | 35° 0 | Sum | P.v. |
| M | 147 | 105 | 103 | 99 | 60 | 51 | 65 | 62 | 43 | 39 | 2023 | 100 |
| N | 75.5 | 62.9 | 56.4 | 51.4 | 39.1 | 37.9 | 39.2 | 37.6 | 36.0 | 28.7 | 743.2 | 37.2 |
For angles less than 37° one finds, in the manner above described, numbers that are a little inferior to the tabulated ones, which are found by means of the absorption-coefficients of Table II. and the values of N. In this way the sum of the M's is a little greater (6.8 per cent.) than it would be according to the calculation given above. This non-agreement results probably from the circumstance that the spectrum in the observations was not quite pure.
The value 37.2 may possibly be affected with a relatively great error in consequence of the uncertainty of the M-values. In the following calculations it is not so much the value 37.2 that plays the important part, but rather the diminution or the value caused by increasing the quantities K and W. For comparison, it may be mentioned that Langley has estimated the quantity of heat from the moon that passed through the atmosphere (of mean composition) in his researches to be 38 per cent. As the mean atmosphere in Langley's observations corresponded with higher values of K and W than K = 1 and W = 0.3, it will be seen that he attributed to the atmosphere a greater transparence for opaque rays than I have done. In accordance with Langley's estimation, we should expect for K= l and W = 0.3 a value of about 44 instead of 37.2. How great an influence this difference may exert will be investigated in what follow.
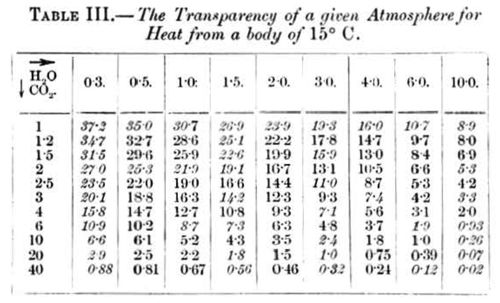
The absorption-coefficients quoted in Table II. are valid for an interval of K between about 1.l and 2.25), and for W between 0.3 and 2.22. In this interval one may, with the help of those coefficients and the values of N given above, calculate the value of N for another value of K and W, and so in this way obtain by means of summation the total heat that passes through an atmosphere of given condition. For further calculations I have also computed values of N for atmospheres that contain greater quantities of carbonic acid and aqueous vapour. These values must be considered as extrapolated. In the following table (Table III.) I have given the values of N. The numbers printed in italics are found directly in the manner described, those in ordinary type are interpolated from them with the help of Pouillet's exponential formula. The table has two headings, one which runs horizontally and represents the quantity of aqueous vapour (W), and another that run vertically and represents the quantity of carbonic acid (K) in the atmosphere.
Quite different from this dark heat is the behaviour of the heat from the sun on passing through new parts of the earth's atmosphere. The first parts of the atmosphere exert without doubt a selective absorption of some ultra-red rays, but as soon as these are extinguished the heat seems not to diminish as it traverses new quantities of the gases under discussion. This can easily be shown for aqueous vapour with the help of Langley's actinometric observations from Mountain Camp and Lone Pine in Colorado. These observations were executed at Lone Pine from the 18th of August to the 6th of September 1882 at 7h 15m and 7h 45m A.M., at 11h 45m A.M. and 12h 15m pm., and at 4h 15m and 4h 45m P.M. At Mountain Camp the observations were carried out from the 22nd to the 25th of August at the same times of the day, except that only one observation was performed in the morning (at Sh 0m). I have divided these observations into two groups for each station according to the humidity of the air. In the following little table are quotes, first the place of observation, and after this under D the mean date of the observations (August 1882), under W the quantity of water, under I the radiation observed by means of the actinometer, under I1 the second observation of the same quantity.

At a very low humidity (Mountain Camp) it is evident that the absorbing power of the aqueous vapour has an influence, for the figures for greater humidity are (with an insignificant exception) inferior to those for less humidity. But for the observations from Lone Pine the contrary seems to be true. It is not permissible to assume that the radiation can be strengthened by its passage through aqueous vapour, but the observed effect must be caused by some secondary circumstance. Probably the air is in general more pure if there is more water-vapour in it than if there is less. The selective diffusion diminishes in consequence of this greater purity, and this secondary effect more than counterbalances the insignificant absorption that the radiation suffers from the increase of the water-vapour. It is noteworthy that Elster and Geitel have proved that invisible actinic rays of very high refrangibility traverse the air much more easily if it is humid than if it is dry. Langley's figures demonstrate meanwhile that the influence of aqueous vapour on the radiation from the sun is insensible as soon as it has exceeded a value of about 0 4.
Probably the same reasoning will bold good for carbonic acid, for the absorption spectrum of both gases is of the same general character. Moreover, the absorption by carbonic acid occurs at considerably greater wave-lengths, and consequently for much less important parts of the sun's spectrum than the absorption by water-vapour. It is, therefore, justifiable to assume that the radiation from the sun suffers no appreciable diminution if K and W increase from a rather insignificant value (K = l, W = 0 4) to higher ones.
Before we proceed further we need to examine another question. Let the carbonic acid in the air be, for instance, the same as now (K = 1 for vertical rays), and the quantity of water-vapour be 10 grammes per cubic metre (W = 1 for vertical rays). Then the vertical rays from the earth traverse the quantities K = l and W = l; rays that escape under an angle of 30° with the horizon (air-mass = 2) traverse the quantities K = 2, W = 2; and so forth. The different rays that emanate from a point of the earth's surface suffer, therefore, a different absorption-the greater, the more the path of the ray declines from the vertical line. It may then be asked how long a path must the total radiation make, that the absorbed fraction of it is the same as the absorbed fraction of the total mass of rays that emanate to space in different directions. For the omitted rays we will suppose, that the cosine law of Lambert holds good. With the aid of Table III. we may calculate the absorbed fraction of any ray, and then sum up the total absorbed heat and determine how great a fraction it is of the total radiation. In this way we find for our example the path (air-mass) 1.61. In other words, the total absorbed part of the whole radiation is just as great as if the total radiation traversed the quantities 1.61 of aqueous vapour and of carbonic acid. This number depends upon the composition of the atmosphere, so that it becomes less the greater the quantity of aqueous vapour and carbonic acid in the air. In the following table (IV.) we find this number for different quantities of both gases.
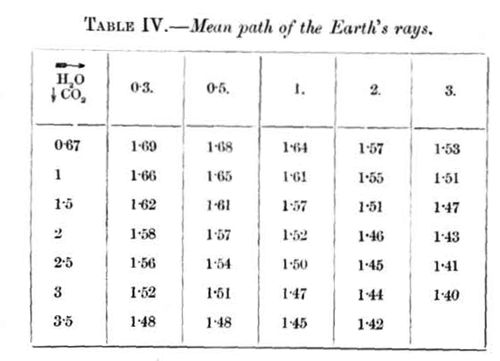
If the absorption of the atmosphere approaches zero, this number approaches the value 2.
III. Thermal Equilibrium on the Surface and in the Atmosphere of the Earth.
As we now have a sufficient knowledge of the absorption of heat by the atmosphere, it remains to examine how the temperature of the ground depends on the absorptive power oft the air. Such an investigation has been already performed by Pouillet, but it must be made anew, for Pouillet used hypotheses that are not in agreement with our present knowledge.
In our deduction we will assume that the heat that is conducted from the interior of the earth to its surface may be wholly neglected. If a change occurs in the temperature of the earth's surface, the upper layers of the earth's crust will evidently also change their temperature; but this later process will pass away in a very short time in comparison with the time that is necessary for the alteration of the surface temperature, so that at any time the heat that is transported from the interior to the surface (positive in the winter, negative in the summer) must remain independent of the small secular variations of the surface temperature, and in the course of a year be very nearly equal to zero.
Likewise we will suppose that the heat that is conducted to a given place on the earth's surface or in the atmosphere in consequence of atmospheric or oceanic currents, horizontal or vertical, remains the same in the course of the time considered, and we will also suppose that the clouded part of the sky remains unchanged. It is only the variation of the temperature with the transparency of the air that we shall examine.
All authors agree in the view that there prevails an equi1ibrium in the temperature of the earth and of its atmosphere. The atmosphere must, therefore, radiate as much heat to space as it gains partly through the absorption of the sun's rays, partly through the radiation from the hotter surface of the earth and by means of ascending currents of air heated by contact with the ground. On the other hand the earth lose just as much heat by radiation to space and to the atmosphere as it gains by absorption of the sun's rays. If we consider a given place in the atmosphere or on the ground we must also take into consideration the quantities of heat that are carried to this place by means of oceanic or atmospheric currents. For the radiation we will suppose that Stefan's law of radiation, which is now generally accepted, holds good, or in other words that the quantity of heat (W) that radiates from a body of the albedo (1 - ν) and temperature T (absolute) to another body of the absorption-coefficient ν and absolute temperature θ is
- W = ν·β·γ·(T4 - θ4)
where γ is the so-called radiation constant (1.21·l0-12 per sec. and cm2). Empty space may be regarded as having the absolute temperature 0°.
Provisionally we regard the air as a uniform envelope of the temperature θ and the absorption-coefficient a for solar heat; so that if A calories arrive from the sun in a column of 1 cm2 cross-section, αA are absorbed by the atmosphere and (1 - α)A reach the earth's surface. In the A calories there is therefore not included that part of the sun's heat which by means of selective reflexion in the atmosphere is thrown out towards space. Further, let β designate the absorption-coefficient of the air for the heat that radiates from the earth's surface; β is also the emission-coefficient of the air for radiation of low temperature-strictly 15°; but as the spectral distribution of the heat varies rather slowly with the temperature, β may be looked on as the emission-coefficient also at the temperature of the air. Let the albedo of the earth's crust be designated by (1 - ν), and the quantities of heat that are conveyed to the air and to the earth's surface at the point considered be M and N respectively. As unit of time we may 1ake any period: the best choice in the following calculation is perhaps to take three months for this purpose. As unit of surface we may take 1 cm2, and for the heat in the air that contained in a column of l cm2 cross-section and the height of the atmosphere. The heat that is reflected from the ground is not appreciably absorbed by the air (see p. 252), for it has previously traversed great quantities of water-vapour and carbonic acid, but a part of it may be returned to the ground by means of diffuse reflexion. Let this part not be included in the albedo (1 - ν). γ, A, ν, M, N, and α are to be considered as constants, β as the independent, and θ and T as the independent variables.
Then we find for the column of air
- β · γ · θ4 = β · γ · ν · (T4-θ4) + α · A + M. (1)
The first member of this equation represents the heat radiated from the air (emission-coefficient γ, temperature θ) to space (temperature 0). The second one gives the heat radiated from the soil (l cm2, temperature T, albedo 1 - ν) to the air; the third and fourth give the amount of the sun's radiation absorbed by the air, and the quantity of heat obtained by conduction (air-currents) from other part of the air or from the ground. In the same manner we find for the earth's surface
- β · γ · ν · (T4 - θ4) + (1 - β) · γ · ν · T4 = (1 - α) · ν · A + N (2)
The first and second members represent the radiated quantities of heat that go to the air and to space respectively, (1 - α)ν A is the part of the sun's radiation absorbed, and N the heat conducted to the point considered from other parts of the soil or from the air by means of water- or air-currents.
Combining both these equations for the elimination of θ, which has no considerable interest, we find for T4
-
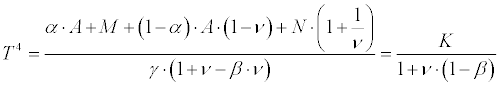 (3)
(3)
For the earth's solid crust we may, without sensible error, put ν equal to 1, if we except the snowfields, for which we assume ν = 0.5. For the water-covered parts of the earth I have calculated the mean value of ν to be 0.925 by aid of the figures of Zenker. We have, also, in the following to make use of the albedo of the clouds. I do not know if this has ever been measured, but it probably does not differ very much from that of fresh fallen snow, which Zollner has determined to be 0.78, i. e. ν = 0.22. For old snow the albedo is much less or ν much greater; therefore we have assumed 0.5 as a mean value.
The last formula shows that the temperature of the earth augments with β, and the more rapidly the greater ν is. For an increase of 1° if ν = 1 we find the following increases for the values of ν = 0.925, 0.5, and 0.22 respectively: -
| β | ν = 0.95 | ν = 0.5 | ν = 0.2 |
| 0.65 | 0.944 | 0.575 | 0.275 |
| 0.75 | 0.940 | 0.556 | 0.261 |
| 0.85 | 0.934 | 0.535 | 0.245 |
| 0.95 | 0.928 | 0.512 | 0.228 |
| 1.00 | 0.925 | 0.500 | 0.220 |
This reasoning holds good if the part of the earth's surface considered does not alter its albedo as a consequence of the altered temperature. In that case entirely different circumstances enter. If, for instance, an element of the surface which is not now snow-covered, in consequence of falling temperature becomes clothed with snow, we must in the last formula not only alter β but also ν. In this case we must remember that α is very small compared to β. For α we will choose the value 0.40 in accordance with Langley's estimate. Certainly a great part of this value depends upon the diffusely reflected part of the sun's heat, which is absorbed by the earth's atmosphere, and therefore should not be included in α as we have defined it above. On the other hand, the sun may in general stand a little lower than in Langley's measurements, which were executed with a relatively high sun, and in consequence of this α may be a little greater, so that these circumstances may compensate each other. For γ we will choose the value 0.70, which corresponds when K = 1 and W = 0.3 (a little below the freezing-point) with the factor 1.66 (see p. 253). In this case we find the relation between T (uncovered) and T11 (snow-covered surface) to be
if M = ΦA. We have to bear in mind that the mean M for the whole earth is zero, for the equatorial regions negative and for the polar regions positive. For a mean latitude M = O, and in this case T1 becomes 267.3 if T = 273, that is the temperature decreases in consequence of the snow-covering by 5.7° C. The decrease of temperature from this cause will be valid until Φ = 1, i. e. till the heat delivered by convection to the air exceeds the whole radiation of the sun. This can only occur in the winter and in polar regions.
But this is a secondary phenomenon. The chief effect that we examine is the direct influence or an alteration of β upon the temperature T of the earth's surface. If we start from a value T = 273 and β = 0.70, wo find the alteration (t) in the temperature which is caused by the variation of β to the following values to be
| β = 0 60 | t = - 5° C. |
| 0.80 | + 5.6 |
| 0.90 | + 11.7 |
| 1.00 | + 18.6 |
These values are calculated for ν = 1, i. e. for the solid crust of the earth's surface, except the snowfields. For surfaces with another value of ν, as for instance the ocean or the snowfields, we have to multiply this value t by a fraction given above.
We have now shortly to consider the influence of the clouds. A great part of the earth's surface receives no heat directly from the sun, because the sun's rays are stopped by clouds. How great a part of the earth's surface is covered by clouds we may find from Teisserenc de Bort's work on Nebulosity. From tab. 17 of this publication I have determined the mean nebulosity for different latitudes, and found:
| Latitude | 60 | 45 | 30 | 15 | 0 | -15 | -30 | -45 | -60 |
| Nebulosity | 0.608 | 0.48 | 0.402 | 0.511 | 0.581 | 0.463 | 0.53 | 0.701 |
For the part of the earth between 60° S, and 60° N, we find the mean value 0.525, i. e. 525 per cent. of the sky is clouded. The heat-effect of these clouds may be estimated in the following manner. Suppose a cloud lies over a part of the earths surface and that no connexion exist between this shadowed part and the neighbouring parts, then a thermal equilibrium will exist between the temperature of the cloud and of the underlying ground. They will radiate to each other and the cloud also to the upper air and to space, and the radiation between cloud and earth may, on account of the slight difference of temperature, be taken as proportional to this difference. Other exchanges of heat by means of air-currents are also, as a first approximation, proportional to this difference. If we therefore suppose the temperature of the cloud to alter (other circumstances, as its height and composition, remaining unchanged), the temperature of the ground under it must also alter in the same manner if the same supply of heat to both subsists-if there were no supply to the ground from neighbouring parts, the cloud and the ground would finally assume the same mean temperature. If, therefore, the temperature of the clouds varies in a determined manner (without alteration of their other properties, as height, compactness, &c.), the ground will undergo the same variations of temperature. Now it will be shown in the sequel that a variation of the carbonic acid of the atmosphere in the same proportion produces nearly the same thermal effect independently of its absolute magnitude (see p. 265). Therefore we may calculate the temperature-variation in this case as if the clouds covered the ground with a thin film of the albedo 0.78 (ν = 0.22 see p. 256). As now on the average K = 1 and W = 1 nearly, and in this case β is about 0,79), the effect on the clouded part will be only 0.25 of the effect on parts that have ν = 1. If a like correction is introduced for the ocean (ν = 0.925) on the supposition that the unclouded part of the earth consists of as much water as of solid ground (which is approximately true, for the clouds are by preference stored up over the ocean), we find a mean effect of, in round numbers, 60 p. c. of that which would exist if the whole earth's surface had ν = 1. The snow-covered parts are not considered, for on the one hand, these parts are mostly clouded to about 65 p. c.; further, they constitute only a very small part of the earth (for the whole year on the average only about 4 p. c.), so that the correction for this case would not exceed 0.5 p. c. in the last number 60. And further, on the border countries between snowfields and free soil secondary effects come into play (see p. 257) which compensate, and perhaps overcome, the moderating effect of the snow.
In the foregoing we have supposed that the air is to be regarded as an envelope of perfectly uniform temperature. This is of course not true, and we now proceed to an examination of the probable correction that must be introduced for elimination of the errors caused by this inexactness. It is evident that the parts of the air which radiate to space are chiefly the external ones, and on the other hand the layers of air which absorb the greatest part of the earth's radiation do not lie very high. From this cause both the radiation from air to space (β · γ · θ4 in eq. l) and also the radiation of the earth to the air (β · γ · ν(T4 - θ4) in eq. 2), are greatly reduced, and the air has a much greater effect as protecting against the loss of heat to space than is assumed in these equations, and consequently also in eq. (3). If we knew the difference of temperature between the two layers of the air that radiate to space and absorb the earth's radiation, it would be easy to introduce the necessary correction in formulae (1), (2), and (3). For this purpose I have adduced the following consideration.
As at the mean composition of the atmosphere (K = 1, W = 1) about 80 p. c. of the earth's radiation is absorbed in the air, we may as mean temperature of the absorbing layer choose the temperature at the height where 40 p. c. of the heat is absorbed. Since emission and absorption follow the same quantitative laws, we may as mean temperature of the emitting layer choose the temperature at the height where radiation entering from space in the opposite direction to the actual emission is absorbed to the extent of 40 p. c.
Langley has made four measurements of the absorptive power of water-vapour for radiation from a hot Leslie cube of 100° C. These give nearly the same absorption-coefficient if Pouillet's formula is used for the calculation. From these numbers we calculate that for the absorption of 40 p. c. of the radiation it would be necessary to intercalate so much water-vapour between radiator and bolometer that, when condensed, it would form a layer of water 3.05 millimetres thick. If we now suppose as mean for the whole earth K = 1 and W = l (see Table VI.), we find that vertical rays from the earth, if it were at 100°, must traverse 305 metres of air to lose 40 p. c. Now the earth is only at 15° C, but this cannot make any great difference. Since the radiation emanates in all directions, we have to divide 305 by l.16 and get in this way 209 metres. In consequence of the lowering of the quantity of water-vapour with the height we must apply a slight correction, so that the final result is 233 metres. Of course this number is a mean value, and higher values will hold good for colder, lower for warmer parts of the earth. In so small a distance from the earth, then, 40 p. c. of the earth's radiation should be stopped. Now it is not wholly correct to calculate with Pouillet's formula (it is rather strange that Langley's figures agree so well with it), which gives necessarily too low values. But, on the other hand, we have not at all considered the absorption by the carbonic acid in this part, and this may compensate for the error mentioned. In the highest layers of the atmosphere there is very little water-vapour, so that we must calculate with carbonic acid as the chief absorbent. From a measurement by Ångström, we learn that the absorption-coefficients of water-vapour and of carbonic acid in equal quantities (equal number of molecules) are in the proportion 81 : 62. This ratio is valid for the least hot radiator that Ångström used, and there is no doubt that the radiation of the earth is much less frangible. But, in the absence of a more appropriate determination we may use this for our purpose; it is probable that for a less hot radiator the absorption power of the carbonic acid would come out a little greater compared with that of water-vapour, for the absorption-bands of C02 are, on the whole, less refrangible than those of H2O (see pp. 246 - 248). Using the number 0.03 vol. p. c. for the quantity of Carbonic acid in the atmosphere, we find the rays which emanate from the upper part of the air are derived to the extent of 40 p. c. from a layer that constitutes 0.145 part of the atmosphere. This corresponds to a height of about 15,000 metres. Concerning this value we may make the same remark as on the foregoing value. In this case we have neglected the absorption by the small quantities of water-vapour in the higher atmosphere. The temperature-difference of these two layers-the one absorbing, the other radiating-is, according to Glaisher's measurements (with a little extrapolation), about 42° C.
For the clouds we get naturally slightly modified numbers. We ought to take the mean height of the clouds that are illuminated by the sun. As such clouds I have chosen the summits of the cumuli that lie at an average height of 1,855 metres, with a maximum height of 3,6ll metres and a minimum of 900 metres. I have made calculations for mean values of 2,000 and 4,000 metres (corresponding to differences of temperature of 30° C. and 20° C instead of 42° C. for the earth's surface).
If we now wish to adjust our formulae (1) to (3), we have in (1) and (2) to introduce θ as the mean temperature of the radiating layer and (θ + 42), (θ + 30), or (θ + 2O) respectively for the mean temperature of the absorbing layer. In the first case we should use ν = 1 and ν = 0.925 respectively, in the second and the third case ν = 0.22.
We then find instead of the formula (3)
another very similar formula
-
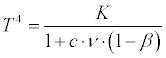 (4)
(4)
where c is a constant with the values 1.88, 1.58, and 1.37 respectively for the three cases. In this way we find the following corrected values which represent the variation of temperature, if the solid ground changes its temperature 1° C. in consequence of a variation of β as calculated by means of formula (3).
| β = | Solid ground ν = 1 | Water ν = 0.925 | Snow ν = 0.5 | Clouds (ν = 0.22 at height of | ||
| 0m | 2,000m | 4,000m | ||||
| 0.65 | 1.53 | 1.46 | 0.95 | 0.49 | 0.42 | 0.38 |
| 0.75 | 1.60 | 1.52 | 0.95 | 0.47 | 0.40 | 0.35 |
| 0.85 | 1.69 | 1.59 | 0.94 | 0.46 | 0.38 | 0.33 |
| 0.95 | 1.81 | 1.68 | 0.94 | 0.43 | 0.36 | 0.31 |
| 1.00 | 1.88 | 1.74 | 0.41 | 0.35 | 0.30 | |
If we now assume as a mean for the whole earth K = 1 and W = 1, we got β = 0.785, and taking the cloud part to be 52.5 p. c. and the clouds to have a height of 2,000 metres further assuming the unclouded reminder of the earth's surface to consist equally of land und water, we find as average variation of temperature
- 1.63 · 0,2385 + 1,54 · 0.2385 + 0.39 · 0.525 = 0.979,
or very nearly the same effect as we may calculate directly from the formula (3). On this ground I have used the simpler formula.
In the foregoing I have remarked that according to my estimation the air is less transparent for dark heat than on Langley's estimate and nearly in the proportion 37.2 : 44. How great an influence this difference may exercise is very easily calculated with the help of formula (3) or (4). According to Langley's valuation, the effect should be nearly 15 p. c. greater than according to mine. Now I think that my estimate agrees better with the great absorption that Langley has found for heat from terrestrial radiating bodies (see p. 260), and in all circumstances I have preferred to slightly underestimate than to overrate the effect in question.
IV. Calculation of the Variation of Temperature that would ensue in consequence of a given Variation of the Carbonic Acid in the Air.
We now possess all the necessary data for an estimation of the effect on the earth's temperature which would be the result of a given variation of the aerial carbonic acid. We only need to determine the absorption-coefficient for a certain place with the help of Table III. if we know the quantity of carbonic acid (K = 1 now) and water-vapour (W) of this place. By the aid of Table IV. we at first determine the factor ρ that gives the mean path of the radiation from the earth through the air and multiply the given K- and W-values by this factor. Then we determine the value of β which corresponds to ρ · K and ρ · W. Suppose now that the carbonic acid had another concentration K1.(e. g. K1 = 1.5). Then we at first suppose W unaltered and seek the new value of ρ, say ρ1, that is valid on this supposition. Next we have to seek β1, which corresponds to ρ1 · K1 (1.5 · ρ1) and ρ1 · W. From formula (3) we can then easily calculate the alteration (t) (here increase) in the temperature at the given place which will accompany the variation of β from β to β1. In consequence of the variation (t) in the temperature, W must also undergo a variation. As the relative humidity does not vary much, unless the distribution of land and water changes (see table 8 of my original memoir), I have supposed that this quantity remains constant, and thereby determined the new value W1 of W. A fresh approximation gives in most cases values of W1 and β1 which may be regarded as definitive. In this way, therefore, we get the variation of temperature as soon as we know the actual temperature and humidity at the given place.
In order to obtain values for the temperature for the whole earth, I have calculated from Dr. Buchan's charts of the mean temperature at different places in every month the mean temperature in every district that is contained between two parallels differing by 10° and two meridians differing by 20 degrees, (e. g., between 0° and 10° N. and 160° and 180° W.). The humidity has not as yet been sufficiently examined for the whole earth; and I have therefore collected a great many measurements of the relative humidity at different places (about 780) on the earth and marked them down in maps of the world, and thereafter estimated the mean values for every district. These quantities I have tabulated for the four seasons, Dec.-Feb., March-May, June-Aug., and Sept.-Nov. The detailed table and the observations used are to be found in my original memoir: here I reproduce only the mean values for every tenth parallel (Table VI.).
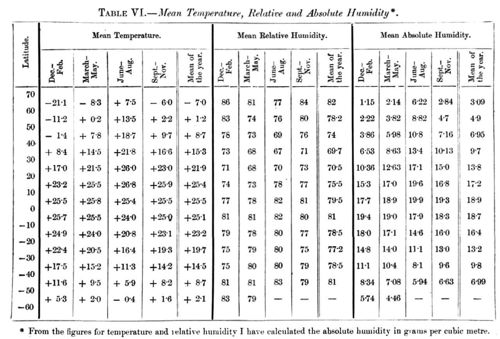
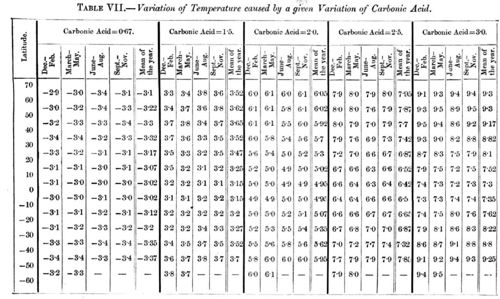
By means of these values, I have calculated the mean alteration of temperature that would follow if the quantity of carbonic acid varied from its present mean value (K = 1) to another, viz. to K = 0.67, 1.5, 2, 2.5, and 3 respectively. This calculation is made for every tenth parallel, and separately for the four seasons of the year. The variation is given in Table VII.
A glance at this Table shows that the influence is nearly the same over the whole earth. The influence has a minimum near the equator, and increases from this to a flat maximum that lies the further from the equator the higher the quantity of carbonic acid in the air. For K = 0.67 the maximum effect lies about the 40th parallel, for K = 1.5 on the 50th, for K = 2 on the 60th, and for higher K-values above the 70th parallel. The influence is in general greater in the winter than in the summer, except in the case of the parts that lie between the maximum and the pole. The influence will also be greater the higher the value of ν, that is in general somewhat greater for land than for ocean. On account of the nebulosity of the Southern hemisphere, the effect will be less there than in the Northern hemisphere. An increase in the quantity of carbonic acid will of course diminish the difference in temperature between day and night. A very important secondary elevation of the effect will be produced in those places that alter their albedo by the extension or regression of the snow-covering (see p. 257), and this secondary effect will probably remove the maximum effect from lower parallels to the neighbourhood of the poles.
It must be remembered that the above calculations are found by interpolation from Langley's numbers for the values K = 0.67 and K = 1.5, and that the other numbers must be regarded as extrapolated. The use of Pouillet's formula makes the values for K = 0.67 probably a little too small, those for K = 1.5 a little too great. This is also without doubt the case for the extrapolated values, which correspond to higher values of K.
We may now inquire how great must the variation of the carbonic acid in the atmosphere be to cause a given change of the temperature. The answer may be found by interpolation in Table VII. To facilitate such an inquiry, we may make a simple observation. If the quantity of carbonic acid decreases from 1 to 0.67, the fall of temperature is nearly the same as the increase of temperature if this quantity augments to 1.5. And to get a new increase of the order of magnitude (3° 4), it will be necessary to alter the quantity of carbonic acid till it reaches a value nearly midway between 2 and 2.5.
Thus if the quantity of carbonic acid increases in geometric progression, the augmentation of the temperature wi1l increase nearly in arithmetic progression. This rule-which naturally holds good only in the part investigated-will be useful for the following summary estimations.
V. Geological Consequences.
I should certainly not have undertaken these tedious calculations if an extraordinary interest had not been connected with them. In the Physical Society of Stockholm there have been occasionally very lively discussions on the probable causes of the Ice Age; and these discussions have, in my opinion, led to the conclusion that there exists as yet no satisfactory hypothesis that could explain how the climatic conditions for an ice age could be realized in so short a time as that which has elapsed from the days of the glacial epoch. The common view hitherto has been that the earth has cooled in the lapse of time; and if one did not know that the reverse has been the case, one would certainly assert that this cooling must go on continuously. Conversations with my friend and colleague Professor [Arvid Gustaf] Högbom, together with the discussions above referred to, led me to make a preliminary estimate of the probable effect of a variation of the atmospheric carbonic acid on the temperature of the earth. As this estimation led to the belief that one might in this way probably find an explanation for temperature variations of 0° - 10° C., I worked out the calculation more in detail, and lay it now before the public and the critics.
From geological researches the fact is well established that in Tertiary times there existed a vegetation and an animal life in the temperate and arctic zones that must have been conditioned by a much higher temperature than the present in the same regions. The temperature in the arctic zones appears to have exceeded the present temperature by about 8 or 9 degrees. To this genial time the ice age succeeded, and this was one or more times interrupted by interglacial periods with a climate of about the same character as the present, sometimes even milder. When the ice age had its greatest extent, the countries that now enjoy the highest civilization were covered with ice. This was the case with Ireland, Britain (except a small part in the south), Holland, Denmark, Sweden and Norway, Russia (to Kiev, Orel, and Nijni Novgorod), Germany and Austria (to the Harz, Erz-Geb1rge, Dresden, and Cracow) . At the same time an ice-cap from the Alps covered Switzerland, parts of France, Bavaria south of the Danube, the Tyrol Styria and other Austrian countries, and descended into the northern part of Italy. Simultaneously, too, North America was covered with ice on the west coast to the 47th parallel, on the east coast to the 40th, and in the central part to the 37th (confluence of the Mississippi and Ohio rivers). In the most different parts of the world, too, we have found traces of a great ice age, as in the Caucasus, Asia Minor, Syria, the Himalayas, India, Thian Shan, Altai, Atlas, on Mount Kenia and Kilimandjaro (both very near to the equator), in South Africa, Australia, New Zealand, Kerguelen, Falkland Islands, Patagonia and other parts of South America. The geologists in general are inclined to think that these glaciations were simultaneous on the whole earth; and this most natural view would probably have been generally accepted, if the theory of James Croll, which demands a genial ago on the Southern hemisphere at the same time as an ice age on the Northern and vice versa had not influenced opinion. By measurements of the displacement of the snow-line we arrive at the result, -and this is very concordant for different places- that the temperature at that time must have been 4° - 5° C. lower than at present. The last glaciation must have taken place in rather recent times geologically speaking, so that the human race certainly had appeared at that period. Certain American geologists hold the opinion that since the close of the ice age only some 7,000 to 10,000 years have elapsed, but this most probably is greatly underestimated.
One may now ask, How much must the Carbonic acid vary according to our figure , in order that the temperature should attain the same values as in the Tertiary and Ice ages respectively? A simple calculation shows that the temperature in the arctic regions would rise about 8° to 9° C., if the carbonic acid increased to 2.5 or 3 times its present value. In order to get the temperature of the ice age between the 40th and 50th parallels, the carbonic acid in the air should sink to 0.62 - 0.55 of its present value (lowering of temperature 4° - 5° C.). The demands of the geologists, that at the genial epochs the climate should be more uniform than now, accords very well with our theory. The geographical annual and diurnal ranges of temperature would be partly smoothed away, if the quantity of carbonic acid was augmented. The reverse would be the case (at least to a latitude of 50° from the equator), if the carbonic acid diminished in amount. But in both these cases I incline to think that the secondary action (see p. 257) due to the regress or the progress of the snow-covering would play the most important role. The theory demands also that, roughly speaking, the whole earth should have undergone about the same variations of temperature, so that according to it genial or glacial epochs must have occurred simultaneously on the whole earth. Because of the greater nebulosity of the Southern hemisphere, the variations must there have been a little less (about 15 per cent.) than in the Northern hemisphere. The ocean currents, too, must there, as at the present time, have effaced the differences in temperature at different latitudes to a greater extent than in the Northern hemisphere. This effect also results from the greater nebulosity in the arctic zones than in the neighbourhood of the equator.
There is now an important question which should be answered, namely:- Is it probable that such great variations in the quantity of carbonic acid as our theory requires have occurred in relatively short geological time? The answer to this question is given by Prof. Högbom. As his memoir on this question may not be accessible to most readers of those pages, I have summed up and translated his utterances which are of most importance to our subject:-
"Although it is not possible to obtain exact quantitative expressions for the reactions in nature by which carbonic acid is developed or consumed, nevertheless there are some factors, of which one may get an approximately true estimate and from which certain conclusions that throw light on the question may be drawn. In the first place, it seems to be of importance to compare the quantity of carbonic acid now present in the air with the quantities that are being transformed. If the former is insignificant in comparison with the latter, then the probability for variations is wholly other than in the opposite case.
"On the supposition that the mean quantity of carbonic acid in the air reaches 0.03 vol. per cent., this number represents 0.045 per cent. by weight, or 0.342 millim. Partial pressure, or 0.466 gramms of carbonic acid for every cm3. of the earth's surface. Reduced to carbon this quantity would give a layer of about 1 millim. thickness over the earth's surface. The quantity of carbon that is fixed in the living organic world can certainly not be estimated with the same degree of exactness; but it is evident that the numbers that might express this quantity ought to be of the same order of magnitude, so that the carbon in the air can neither be conceived of as very great nor as very little, in comparison with the quantity of carbon occurring in organisms. With regard to the great rapidity with which the transformation in organic nature proceeds, the disposable quantity of carbonic acid is not so excessive that changes caused by climatological or other reason in the velocity and value of that transformation might be not able to cause displacements of the equilibrium.
" The following calculation is also very instructive for the appreciation of the relation between the quantity of carbonic acid in the air and the quantities that are transformed. The world's present production of coal reaches in round numbers 500 millions of tons per annum, or 1 ton per km2 of the earth's surface. Transformed in to carbonic acid, this quantity would correspond to about a thousandth part of the carbonic acid in the atmosphere. It represents a layer of limestone of 0.003 millim. thickness over the whole globe, or 1.5 km3 in cubic measure. This quantity of carbonic acid, which is supplied to the atmosphere chiefly by modern industry, may bb regarded as completely compensating the quantity of carbonic acid that is consumed in the formation of limestone (or other mineral carbonates) by the weathering or decomposition of silicates. From the determination of the amounts of dissolved substances, especially carbonates, in a number of rivers in different countries and climates, and of the quantity of water flowing in these rivers and of their drainage-surface compared with the land-surface of the globe, it is estimated that the quantities of dissolved carbonates that are supplied to the ocean in the coarse of a year reach at most the bulk of 3 km3. As it is also proved that the rivers the drainage regions of which consist of silicates convey very unimportant quantities of carbonates compared with these that flow through limestone regions, it is permissible to draw the conclusion, which is also strengthened by other reasons, that only an insignificant part of these 3 km3 of carbonates is formed directly by decomposition of silicates. In other words, only an unimportant part of this quantity of carbonate of lime can be derived from the process of weathering in a year. Even though the number given were on account of inexact or uncertain assumptions erroneous to the extent of 50 per cent. or more, the comparison instituted is of very great interest, as it proves that the most important of all the processes by means of which carbonic acid bas been removed from the atmosphere in all times, namely the chemical weathering of siliceous minerals, is of the same order of magnitude as a process of contrary effect, which is caused by the industrial development of our time and which must be conceived of as being of a temporary nature.
"In comparison with the quantity of carbonic acid which is fixed in limestone (and other carbonates), the carbonic acid of the air vanishes. With regard to the thickness of sedimentary formations and the great part of them that is formed by limestone and other carbonates, it seems not improbable that the total quantity of carbonates would cover the whole earth's surface to a height of hundreds of metres. If we assume 100 metres, - a number that may be inexact in a high degree, but probably is underestimated, - we find that about 25,000 time as much carbonic acid is fixed to lime in the sedimentary formations as exists free in the air. Every molecule of carbonic acid in this mass of limestone has however, existed in and passed through the atmosphere in the course of time. Although we neglect all other factors which may have influenced the quantity of carbonic acid in the air, this number lends but very slight probability to the hypothesis, that this quantity should in former geological epochs have changed within limits which do not differ much from the present amount. As the process of weathering has consumed quantities of carbonic acid many thousand times greater than the amount now disposable in the air, and as this process from different geographical climatological and other causes has in all likelihood proceeded with very different intensity at different epochs, the probability of important variations in the quantity of carbonic acid seems to be very great, even if we take into account the compensating processes which, as we shall see in what follows, are called forth as soon as, for one reason or another the production or consumption of carbonic acid tends to displace the equilibrium to any considerable degree. One often hears the opinion expressed, that the quantity of carbonic acid in the air ought to have been very much greater formerly than now, and that the diminution should arise from the circumstance that carbonic acid has been taken from the air and stored in the earth's crust in the form of coal and carbonates. In many cases this hypothetical diminution is ascribed only to the formation of coal, whilst the much more important formation of carbonates is wholly overlooked. This whole method of reasoning on a continuous diminution of the carbonic acid in the air loses all foundation in fact, notwithstanding that enormous quantities of carbonic acid in the course of time have been fixed in carbonates, if we consider more closely the processes by means of which carbonic acid has in all times been supplied to the atmosphere. From these we may well conclude that enormous variations have occurred, but not that the variation has always proceeded in the same direction.
" Carbonic acid is supplied to the atmosphere by the following processes:- (1) volcanic exhalations and geological phenomena connected therewith; (2) combustion of carbonaceous meteorites in the higher regions of the atmosphere; (3) combustion and decay of organic bodies; (4) decomposition of carbonates; (5) liberation of carbonic acid mechanically inclosed in minerals on their fracture or decomposition. The carbonic acid of the air is consumed chiefly by the following processes:- (6) formation of carbonates from silicates on weathering; and (7) the consumption of carbonic acid by vegetative processes. The ocean, too, plays an important role as a regulator of the quantity of carbonic acid in the air by means of the absorptive power of its water, which gives off carbonic acid as its temperature rises and absorbs it as it cools. The processes named under (4) and (5) are of little significance, so that they may be omitted. So too the processes (3) and (7), for the circulation of matter in the organic world goes on so rapidly that their variations cannot have any sensible influence. From this. we must except periods in which great quantities of organisms were stored up in sedimentary formations and thus subtracted from the circulation, or in which such stored-up products were as now introduced anew into the circulation. The source of carbonic acid named in (2) is wholly incalculable.
"Thus the processes (1), (2), and (6) chiefly remain as balancing each other. As the enormous quantities of carbonic acid (representing a pressure of many atmospheres) that are now fixed in the limestone of the earth's crust cannot be conceived to have existed in the air but as an insignificant fraction of the whole at any one time since organic life appeared on the globe, and since .therefore the consumption through weathering and formation of carbonates must have been compensated by means of continuous supply, we must regard volcanic exhalations as the chief source of carbonic acid for the atmosphere.
"But this source has not flowed regularly and uniformly. Just as single volcanoes have their periods of variation with alternating relative rest and intense activity, in the same manner the globe as a whole seems in certain geological epochs to have exhibited a more violent and general volcanic activity, whilst other epochs have been marked by a comparative quiescence of the volcanic forces. It seems therefore probable that the quantity of carbonic acid in the air has undergone nearly simultaneous variations, or at least that this factor has had an important influence.
"If we pass the above-mentioned processes for consuming and producing carbonic acid under review, we find that they evidently do not stand in such a relation to or dependence on one another that any probability exist for the permanence of an equilibrium of the carbonic acid in the atmosphere. An increase or decrease of the supply continued during geological periods must, although it may not be important, conduce to remarkable alterations of the quantity of carbonic acid in the air, and there is no conceivable hindrance to imagining that this might in a certain geological period have been several times greater, or on the other hand considerably less, than now."
As the question of the probability of quantitative variation of the carbonic acid in the atmosphere is in the most decided manner answered by Prof. Högbom, there remains only one other point to which I wish to draw attention in a few words, namely: Has no one hitherto proposed any acceptable explanation for the occurrence of genial and glacial periods? Fortunately, during the progress of the foregoing calculations, a memoir was published by the distinguished Italian meteorologist L. De Marchi which relieves me from answering the last question. He examined in detail the different theories hitherto proposed-astronomical, physical, or geographical, and of these I here give a short resume. These theories assert that the occurrence of genial or glacial epochs should depend on one or other change in the following circumstances:
- The temperature of the earth's place in space.
- The sun's radiation to the earth (solar constant).
- The obliquity of the earth's axis to the ecliptic.
- The position of the poles on the earth's surface.
- The form of the earth's orbit, especially its eccentricity (James Croll).
- The shape and extension of continents and oceans.
- The covering of the earth's surface (vegetation).
- The direction of the oceanic and aerial currents.
- The position of the equinoxes.
De Marchi arrives at the conclusion that all these hypotheses must be rejected {p. 207). On the other hand, he is of the opinion that a change in the transparency of the atmosphere would possibly give the desired effect. According to his calculations, "a lowering of this transparency would effect a lowering of the temperature on the whole earth, slight in the equatorial regions, and increasing with the latitude into the 70th parallel, nearer the poles again a little less. Further, this lowering would, in non-tropical regions, be less on the continents than on the ocean und would diminish the annual variations of the temperature. This diminution of the air's transparency ought chiefly to be attributed to a greater quantity of aqueous vapour in the air, which would cause not only a direct cooling but also copious precipitation of water and snow on the continents. The origin of this greater quantity of water-vapour is not easy to explain." Luigi De Marchi has arrived at wholly other results than myself, because he has not sufficiently considered the important quality of selective absorption which is possessed by aqueous vapour. And. further, he has forgotten that if aqueous vapour is supplied to the atmosphere, it will be condensed till the former condition is reached, if no other change has taken place. As we have seen, the mean relative humidity between the 40th and 60th parallels on the northern hemisphere is 76 per cent. If, then, the mean temperature sank from its actual value + 5.3 by 4° - 5° C., i. e. to + 1.3 or + 0 3, and the aqueous vapour remained in the air, the relative humidity would increase to 101 or 105 per cent. This is of course impossible, for the relative humidity cannot exceed 100 per cent. in the free air. A fortiori it is impossible to assume that the absolute humidity could have been greater than now in the glacial epoch.
As the hypothesis of James Croll still seems to enjoy a certain favour with English geologists, it may not be without interest to cite the utterance of Luigi De Marchi on this theory, which he, in accordance with its importance, has examined more in detail than the others. He says, and I entirely agree with him on this point:- "Now l think I may conclude that from the point of view of climatology or meteorology, in the present state of these sciences, the hypothesis of James Croll seems to be wholly untenable as well in its principle as in its consequences".
It seems that the great advantage which James Croll's hypothesis promised to geologists, viz. of giving them a natural chronology, predisposed them in favour of its acceptance. But this circumstance, which at first appeared advantageous, seems with the advance of investigation rather to militate against the theory, because it becomes more and more impossible to reconcile the chronology demanded by James Croll's hypothesis with the facts of observation.
I trust that after what has been said the theory proposed in the foregoing pages will prove useful in explaining some points in geological climatology which have hitherto proved most difficult to interpret.
Addendum
As the nebulosity is very different in different latitudes, and also different over the sea and over the continents, it is evident that the influence of a variation in the carbonic acid of the air will be somewhat different from that calculated above, where it is assumed that the nebulosity is the same over the whole globe. I have therefore estimated the nebulosity at different latitudes with the help of the chart published by Teisserenc de Bort, and calculated the following table for
| Table VII. Variation of Temperature caused by a given Variation of Carbonic Acid | |||||||||||||||||||||||||
| Carbonic Acid=0,67 | Carbonic Acid=1,5 | Carbonic Acid=2,0 | Carbonic Acid=2,5 | Carbonic Acid=3,0 | |||||||||||||||||||||
| Latitude | Dec.-Feb. | March-May | June-Aug. | Sept.-Nov. | Mean of the year | Dec.-Feb. | March-May | June-Aug. | Sept.-Nov. | Mean of the year | Dec.-Feb. | March-May | June-Aug. | Sept.-Nov. | Mean of the year | Dec.-Feb. | March-May | June-Aug. | Sept.-Nov. | Mean of the year | Dec.-Feb. | March-May | June-Aug. | Sept.-Nov. | Mean of the year |
| 70 | |||||||||||||||||||||||||
| -2,9 | -3,0 | -3,4 | -3,1 | -3,10 | 3,3 | 3,4 | 3,8 | 3,6 | 3,52 | 6,0 | 6,1 | 6,0 | 6,1 | 6,05 | 7,9 | 8,0 | 7,9 | 8,0 | 7,95 | 9,1 | 9,3 | 9,4 | 9,4 | 9,30 | |
| 60 | |||||||||||||||||||||||||
| -3,0 | -3,2 | -3,4 | -3,3 | -3,22 | 3,4 | 3,7 | 3,6 | 3,8 | 3,62 | 6,1 | 6,1 | 5,8 | 6,1 | 6,02 | 8,0 | 8,0 | 7,6 | 7,9 | 7,87 | 9,3 | 9,5 | 8,9 | 9,5 | 9,30 | |
| 50 | |||||||||||||||||||||||||
| -3,2 | -3,3 | -3,3 | -3,4 | -3,30 | 3,7 | 3,8 | 3,4 | 3,7 | 3,65 | 6,1 | 6,1 | 5,5 | 6,0 | 5,92 | 8,0 | 7,9 | 7,0 | 7,9 | 7,70 | 9,5 | 9,4 | 8,6 | 9,2 | 9,17 | |
| 40 | |||||||||||||||||||||||||
| -3,4 | -3,4 | -3,2 | -3,3 | -3,32 | 3,7 | 3,6 | 3,3 | 3,5 | 3,52 | 6,0 | 5,8 | 5,4 | 5,6 | 5,70 | 7,9 | 7,6 | 6,9 | 7,3 | 7,42 | 9,3 | 9,0 | 8,2 | 8,8 | 8,82 | |
| 30 | |||||||||||||||||||||||||
| -3,3 | -3,2 | -3,1 | -3,1 | -3,17 | 3,5 | 3,3 | 3,2 | 3,5 | 3,47 | 5,6 | 5,4 | 5,0 | 5,2 | 5,30 | 7,2 | 7,0 | 6,6 | 6,7 | 6,87 | 8,7 | 8,3 | 7,5 | 7,9 | 8,10 | |
| 20 | |||||||||||||||||||||||||
| -3,1 | -3,1 | -3,0 | -3,1 | -3,07 | 3,5 | 3,2 | 3,1 | 3,2 | 3,25 | 5,2 | 5,0 | 4,9 | 5,0 | 5,02 | 6,7 | 6,6 | 6,3 | 6,6 | 6,52 | 7,9 | 7,5 | 7,2 | 7,5 | 7,52 | |
| 10 | |||||||||||||||||||||||||
| -3,1 | -3,0 | -3,0 | -3,0 | -3,02 | 3,2 | 3,2 | 3,1 | 3,1 | 3,15 | 5,0 | 5,0 | 4,9 | 4,9 | 4,95 | 6,6 | 6,4 | 6,3 | 6,4 | 6,42 | 7,4 | 7,3 | 7,2 | 7,3 | 7,30 | |
| 0 | |||||||||||||||||||||||||
| -3,0 | -3,0 | -3,1 | -3,0 | -3,02 | 3,1 | 3,1 | 3,2 | 3,2 | 3,15 | 4,9 | 4,9 | 5,0 | 5,0 | 4,95 | 6,4 | 6,4 | 6,6 | 6,6 | 6,50 | 7,3 | 7,3 | 7,4 | 7,4 | 7,35 | |
| -10 | |||||||||||||||||||||||||
| -3,1 | -3,1 | -3,2 | -3,1 | -3,12 | 3,2 | 3,2 | 3,2 | 3,2 | 3,20 | 5,0 | 5,0 | 5,3 | 5,1 | 5,07 | 6,6 | 6,6 | 6,7 | 6,7 | 6,62 | 7,4 | 7,5 | 8,0 | 7,6 | 7,62 | |
| -20 | |||||||||||||||||||||||||
| -3,1 | -3,2 | -3,3 | -3,2 | -3,20 | 3,2 | 3,2 | 3,4 | 3,2 | 3,27 | 5,2 | 5,3 | 5,5 | 5,4 | 5,35 | 6,7 | 6,8 | 7,0 | 7,0 | 6,87 | 7,9 | 8,1 | 8,6 | 8,3 | 8,22 | |
| -30 | |||||||||||||||||||||||||
| -3,3 | -3,3 | -3,4 | -3,4 | -3,35 | 3,4 | 3,5 | 3,7 | 3,5 | 3,52 | 5,5 | 5,6 | 5,8 | 5,6 | 5,52 | 7,0 | 7,2 | 7,7 | 7,4 | 7,32 | 8,6 | 8,7 | 9,4 | 8,8 | 8,80 | |
| -40 | |||||||||||||||||||||||||
| -3,4 | -3,4 | -3,3 | -3,4 | -3,37 | 3,6 | 3,7 | 3,8 | 3,7 | 3,70 | 5,8 | 6,0 | 6,0 | 6,0 | 5,95 | 7,7 | 7,9 | 7,9 | 7,9 | 7,85 | 9,1 | 9,2 | 9,4 | 9,3 | 9,25 | |
| -50 | |||||||||||||||||||||||||
| -3,2 | -3,3 | — | — | — | 3,8 | 3,7 | — | — | — | 6,0 | 6,1 | — | — | — | 7,9 | 8,0 | — | — | — | 9,4 | 9,5 | — | — | — | |
| -60 | |||||||||||||||||||||||||
the value of the variation of temperature, if the carbonic acid decreases to 0.67 or increases to 1.5 times the present quantity. In the first column is printed the latitude; in the second and third the nebulosity over the continent and over the ocean; in the fourth the extension of the continent in hundredths of the whole area. After this comes, in the fifth and sixth columns, the reduction factor with which the figures in the table are to be multiplied for getting the true variation of temperature over continents and over oceans, and, in the seventh column, the mean of both these correction factors. In the eighth and ninth columns the temperature variations for K = 0.67, and in the tenth and eleventh the corresponding values for K = 1.5 are tabulated.
The mean value of the reduction factor N. of equator is for the continent (to 70° N. lat.) 1.098 and for the ocean 0.927, in mean 0.996. For the southern hemisphere (to 60° S. lat.) it is found to be for the continent 1.095, for the ocean 0.871, in mean 0.907. The influence in the southern hemisphere will, therefore, be about 9 per cent. less than in the northern. In consequence of the minimum of nebulosity between 20° and 30° latitude in both hemispheres, the maximum effect of the variation of carbonic acid is displaced towards the equator, so that it falls at about 25° latitude in the two cases or K = 0.67 and K = 1.5.
- Quelle:
- Svante Arrhenius: On the Influence of Carbonic Acid in the Air upon the Temperature of the Ground. Philosophical Magazine and Journal of Science. Series 5, Volume 41, April 1896, pages 237-276.
Zitate
- James Croll: Climate and Time in Their Geological Relations. A Theory of Secular Changes of the Earth's Climate. New York 1893.
- Luigi De Marchi: Le Cause dell'Era Glaciale. Pavia 1895.
- Jean Baptiste Joseph [Joseph] Fourier: The Analytical Theory of Heat. (Übers. Alexander Freeman). Cambridge 1878.
- M. Pouillet: Memoir on solar heat, the radiative effects of the atmosphere, and the temperature of space. In: Scientific Memoires, Vol IV, London 1846. S. 44 - 90.
- Samuel Pierpont Langley: The Bolometer and Radiant Energy. Proceedings of the American Academy of Arts and Sciences Vol. 16 (May, 1880 - Jun., 1881), pp. 342-358.
Svante Arrhenius versucht, in einer Diskussion zur Entstehung von Eiszeiten zwischen den Anhängern der astronomischen Hypothese (James Croll) und den Anhängern der Hypothese der Absorption der Sonnenenergie auf der Erdoberfläche durch Wasserdampf und Kohlendioxid (Arvid Gustaf Högbom auf der Beobachtung über die unterschiedlichen Erwärmungen von mit Luft und Kohlendioxid gefüllten Glaszylindern von Eunice Foote) zu entscheiden. Basierend auf Wärmemengen Messungen mit dem von ihm entwickeln Bolometer von Samuel Pierpont Langley berechnet er die Wärmemenge von der Atmosphäre absorbierte Wärmemenge für eine Erhöhung der Kohlendioxidkonzentration. Langley hatte ein Infrarotspektrometer entwickelt, und konnte zwischen der Stahlungsabsorption von Wasserdampf und Kohlendioxid unterscheiden. Seine Meßreihen auf unterschiedlichen Höhen und geographischen Breiten ließen die Ableitungen von extrapolierten Gleichungen zu.
Der Fehler Arrhenius' liegt in der Annahme dass die gesamte eingestrahlte Wärmenenergie zu einer erhöhten Temperatur des Gasgemisches führt. Das ist nicht der Fall, denn Energie wird nicht vollständig in eine andere Form umgewandelt (hier: Wärmestrahlung in kinetische Energie der Gasatome; 2. Hauptsatz der Thermodynamik). Allerdings kannte er offensichtlich die Arbeit von Eunice Foote.
Ein Großteil des vorliegenden Artikels bezieht sich auf die Normierung der Meßergebnisse. So kann er im Abschnitt IV die Temperatur der Atmosphäre berechnen, die niedrigeren und höheren CO2-Konzentrationen in der Luft entsprächen. Auf der Grundlage seiner Berechnungen schließt sich Arrhenius der im Abschnitt V zitierten Meinung von Högbom an, die Abfolge von Eis- und Warmzeiten beruhe auf wechselnden CO2-Konzentrationen in der Atmosphäre. Zumal auch Luigi De Marchi die astronomische Hypothese Crolls widerlegt.
Hauptargument gegen die astronomischen Ursache der Eiszeiten ist, dass die (damals bekannten) Schwankungen der Schiefe der Ekliptik eine andere, viel geringere, Frequenz haben als die Eiszeiten. Dieses Problem löst die Hypothese von Milutin Milanković durch die Einbeziehung der Konsequenzen der Kontinentaldrifttheorie Alfred Wegeners: Wenn die Kontinentalplatten auf der Oberfläche eines flüssigen Erdkerns schwimmen und ihre Verteilung ändern, dann verändert sich der Drehimpuls des Erdballs. Und diese Änderung erzeugt ein Drehmoment, das senkrecht auf dem Impulsvektor steht. Folglich neigt sich die Erdachse oder richtet sich auf, was gleichbedeutend ist mit einer Veränderung der Schiefe der Ekliptik. Diese verursacht zusammen mit der Präzession und der Nutation der Erdachse eine stärkere Sonnenenergieeinstrahlung - besonders in den Polregionen. Er leitet die Milanković-Zyklen ab, deren Frequenz gut mit dem Eintreten von Kalt- und Warmzeiten übereinstimmt.
[Wärmeabsorption] [Strahlungsabsorption] [CO2 Einfluss]
© Rainer Stumpe, URL: www.rainerstumpe.de/