Sphärische Trigonometrie
Das Poldreieck
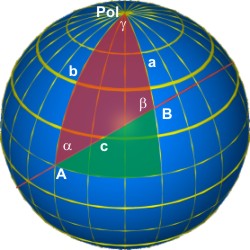 Das sphärische Poldreieck hat den Pol des Kugelkoordinatensystems als eine seiner Ecken. Daraus folgt, dass zwei seiner Seiten Meridiane sind, die den Äquator im rechten Winkel schneiden. (☞ Achtung: nur der Äquator ist von den Breitenkreisen ein Großkreis!)
Das sphärische Poldreieck hat den Pol des Kugelkoordinatensystems als eine seiner Ecken. Daraus folgt, dass zwei seiner Seiten Meridiane sind, die den Äquator im rechten Winkel schneiden. (☞ Achtung: nur der Äquator ist von den Breitenkreisen ein Großkreis!)
Der Dreieckswinkel ∠APB = γ am Pol (er liegt der Seite c gegenüber) ergibt sich einfach aus der Längendifferenz der Punkte A und B. Mit dem Hilfsdreieck (hier grün), dessen eine Kathete parallel zum Äquator liegt, sind die Berechnungen aller Seiten und Winkel möglich. Diese Kathete des grünen Dreiecks ist gleichzeitig eine Seite des gleichschenkligen Dreiecks mit dem Pol als der gegenüberliegenden Ecke. Die andere Kathete ist der Komplementärwinkel der Breite φB, bzw. die Breitendifferenz φA - φB der beiden Punkte A und B.
In der reinen Lehre der sphärischen Trigonometrie gibt es noch das "Polardreieck" und das "rechtseitige" Dreieck (in Ergänzung zum rechtwinkligen). Beide scheinen nur theoretische Bedeutung für den Beweis von Lehrsätzen zu haben. Eine Bedeutung in der Navigation habe ich nicht gefunden.
Das rechtwinklige sphärische Dreieck
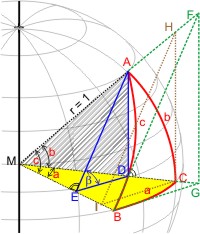
Am Beispiel eines rechtwinkligen sphärischen Dreiecks lassen sich die Zusammenhänge recht übersichtlich darstellen. Das rote Dreieck in der Abbildung rechts hat den rechten Winkel am Punkt C, denn dort schneidet ein Meridian den Äquator. Vom Mittelpunkt M der Kugel mit dem Radius r = 1 sieht man alle Dreiecksseiten unter dem Winkel, der ihrer Länge entspricht.
(Der Umfang U einer Kugel mit dem Radius r = 1 ist ein (Groß-)Kreis mit dem Umfang U = 2·r·π. Da r = 1 ist, gilt U = 2·π = 360°, und ein Kreissegment (z. B. b = AC) hat den Bruchteil b ⁄ 2·π am Gesamtumfang, der dem Bruchteil des Winkels b am Mittelpunkt M vom Gesamtumfang U = 2·π entspricht.)
Legt man in der Ecke B des sphärischen Dreiecks ABC zwei Tangenten an die Kugel, so definiert man eine Ebene BFG. In einer weiteren zu BFG parallelen Ebene liege die Ecke A, und in einer dritten parallelen Ebene liege C. Die drei Ebenen schneiden die Verbindungslinien des Kugelmittelpunkts M mit den drei Ecken des sphärischen Dreiecks ABC, und man erhält drei ähnliche Dreiecke, die zusätzlich rechtwinklig sind: ADE, HCI und FGB. Mit ihrer Hilfe und den Keildreiecken mit dem Mittelpunkt der Kugel als eine der Ecken kann man die Formeln zur Berechnung der Stücke im sphärischen Dreieck herleiten.
- Mit dem Dreieck ADE:
Im rechtwinkligen Dreieck AEM mit den Katheten AE und EM und der Hypotenuse MA = 1 ist der Winkel ∠AME = c, und damit (aus der Definition der Sinusfunktion) die Kathete AE = sin c, und die andere Kathete ME = cos c. Ebenso erhalten wir aus dem Dreieck ADM (Hypotenuse AM = 1): AD = sin b und DM = cos b. Das Dreieck DEM hat den rechten Winkel bei E (der Radius durch den Berührungspunkt steht auf der Tangente senkrecht) und die Hypotenuse DM = cos b. Das heißt: DE = cos b · sin a und ME = cos b · cos a. Nun hat man zwei Beziehungen für ME, die man gleichsetzen kann:
cos c = cos b · cos a
oder in Worten:Im rechtwinkligen sphärischen Dreieck ist der Cosinus der Hypotenuse gleich dem Produkt der Cosinusse der Katheten.Damit ist es gelungen, nur durch Überlegungen an ebenen Dreiecken eine Beziehung der Seiten eines rechtwinkligen sphärischen Dreiecks auf der Kugel mit dem Radius r = 1 abzuleiten. Man nennt sie — weil sie so einfach ist — auch den sphärischen Pythagoras.
- Mit dem Dreieck HCI:
Im Dreieck HCI ist die Strecke CI = sin a die Kathete des rechtwinkligen Dreiecks CIM, dessen Hypotenuse MC = 1 (Einheitsradius). Im rechtwinkligen Dreieck HCM ist CH die Kathete, CM = 1 die andere Kathete, und HM die Hypotenuse. Es gilt: sin b = CH ⁄ HM und cos b = CM ⁄ HM. Diese beiden Gleichungen werden durcheinander dividiert: sin b ⁄ cos b = (CH · HM) ⁄ (CM · HM). HM kann man kürzen, und sin b ⁄ cos b = tan b. Da CM = 1 erhält man tan b = CH.
- Mit dem Dreieck FGB
Im Dreieck FGB ist die Kathete BG = sin a. Mit den Mittelpunktsdreiecken BMG und FMB erhält man analog zu 2.: BG = tan a und FB = tan c.
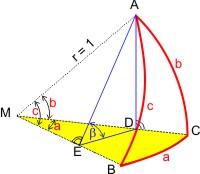
Um zu Beziehungen der Winkel im sphärischen Dreieck zu kommen, betrachten wir das ebene blaue Dreieck ADE in der vereinfachten Abbildung rechts. Der Winkel bei A im ebenen Dreieck entspricht (≑) dem Winkel bei A im sphärischen: ∠BAC ≑ ∠EAD ≑ α (weil für die Längen der Katheten in den rechtwinkligen Dreiecken gilt: AC = AD = b und CB = DE = a, wobei a und b die Winkel am Mittelpunkt M sind). Und da im ebenen rechtwinkligen Dreieck die Winkelsumme 180° beträgt, ist auch ∠ABC ≑ ∠AED ≑ β (denn ∠ACB = ∠ADE = 90°).
Nun bemühen wir wieder die Definition der Winkelfunktionen im rechtwinkligen ebenen Dreieck, und wählen die Definition der Tangensfunktion: tan β = AD ⁄ DE. Die Länge der beiden Katheten kennen wir aus der Herleitung des "sphärischen Pythagoras" oben auf der Seite: AD = sin b und DE = cos b · sin a. Das eingesetzt in die Tangensdefinition ergibt: tan β = (sin b) ⁄ (cos b · sin a) = (sin b ⁄ cos b) ⁄ sin a = tan b ⁄ sin a.
Mit der Gleichung
ist die Beziehung eines Winkels im rechtwinkligen sphärischen Dreieck zu den Längen der beiden Katheten hergestellt. Die gleichen Argumente kann man für den Winkel α anwenden. Man erhält so einen Satz von Gleichungen, mit denen man die Elemente im rechtwinkligen sphärischen Dreieck berechnen kann, wenn man nur zwei kennt.
Dieser Satz Gleichungen wurde von John Neper zusammen mit einer Merkregel und optimiert für die Berechnungen mit der Logarithmentafel (und damit auch für den Rechenschieber!) im Jahr 1641 publiziert. Wir verzichten hier auf die ausführliche Herleitung und wenden uns dem schiefwinkligen sphärischen Dreieck zu.
- Zum Thema gehörende Seiten:
- [sphärische Trigonometrie - Grundlagen]
- [Das rechtwinklige sphärische Dreieck]
- [Das schiefwinklige sphärische Dreieck]
- [Anwendungen der sphärische Trigonometrie] (Orthodrome, Tageslänge, Deklination der Sonne)
- [Anwendungen der sphärische Trigonometrie] (Sonnenhöhe, indischer Kreis)
- [Die Nepersche Regel]
- [Beispielrechnung]
- [Konstruktion mit Projektion der Kugel]