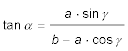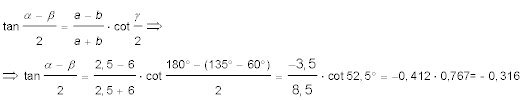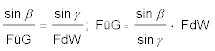Beschickung durch Strom
Versetzung durch Strömung
Für das Koppeln müssen wir die Strömung berücksichtigen um einen realistischen Koppelort zu bekommen. Die Strömung hat ja einen Einfluss auf den gefahrenen Kurs und auf die Geschwindigkeit über Grund. Wir fragen uns also, wo kommen wir beim Steuerkurs hin? (Der Steuerkurs ist der, den wir am Kompass ablesen. Bei geplanter Fahrt ist das der rechtweisende Kurs - rwK - zum Ziel.) Dazu berechnen wir nach dem Sinussatz den KüG und die FüG ehe wir einen Koppelort bestimmen.
|
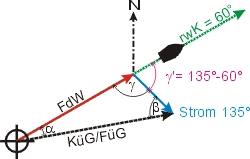
Die Stromangaben bestehen aus einer rw Richtung (SR = Stromrichtung) und einer Geschwindigkeit (SG = Stromgeschwindigkeit, kn). Vom Ausgangsort fährt man mit dem rechtweisenden Kurs (rwK) aus der Karte (KaK, KüG) (oder berechnet) mit einer Geschwindigkeit über Grund (FüG). Den Kurs durchs Wasser (KdW) und die Geschwindigkeit (Fahrt) durchs Wasser (FdW) erhält man durch Addition der Einheitsvektoren (bezogen auf 1 h). Oder durch Berechnen des Dreiecks. |
Der Sinussatz im schiefwinkligen Dreieck setzt leider voraus, dass man zwei Winkel und zwei Seitenlängen kennt. Bekannt sind aber nur zwei Seiten(a = Stromgeschwindigkeit, b = FdW) und der Winkel γ. Zum Glück gibt es den Tangenssatz, der alle drei Winkel aus einem Winkel und zwei Seiten berechnen läßt.
Den Winkel γ erhalten wir aus rw-Kurswinkel und Stromrichtung (beide werden zur Nordrichtung angegeben), im Beispiel γ = 180° - (SR - rwK). Die Seiten a und b sind die Stromgeschwindigkeit und die FdW.
Wir erhalten so ![]() . Da γ = 180° - (α + β), berechnen wir auch (α + β) = 180° - γ. Die Summe der beiden
Ausdrücke (α + β) + (α - β) = α + β + α - β = 2·α liefert den Kurskorrekturwinkel α, die Differenz (α + β) - (α - β) = 2·β liefert den Winkel, mit dem wir nach dem Sinussatz die FüG berechnen können:
. Da γ = 180° - (α + β), berechnen wir auch (α + β) = 180° - γ. Die Summe der beiden
Ausdrücke (α + β) + (α - β) = α + β + α - β = 2·α liefert den Kurskorrekturwinkel α, die Differenz (α + β) - (α - β) = 2·β liefert den Winkel, mit dem wir nach dem Sinussatz die FüG berechnen können:
Zum Berechnen des Winkels α aus den Seiten a und b gibt es noch eine weitere Formel:
Man erhält sie, wenn man in dem Dreieck eine Höhe so einzeichnet, dass der Winkel β geteilt wird (also von der Ecke B auf die Seite AC). Nun hat man zwei rechtwinklige Dreiecke und kann die Höhe einmal mit α und einmal mit γ berechnen. Da beide Ausdrücke gleich sein müssen, bedarf es nur einiger Arithmetik, um die Formel zu erhalten.
Hat man α berechnet (γ kennen wir ja schon), ist es leicht β zu bestimmen und den Sinussatz anzuwenden.
Beispielrechnung
Ein Boot segelt mit 6 kn (FdW) (rw) Kurs 60° durch einen Kanal zwischen 2 Inseln, in der ein Strom mit 2,5 kn in Richtung 135° versetzt. Welchen Kurs und welche Geschwindigkeit über Grund fährt das Boot?
Bekannt sind der Winkel γ = 180° - (SR - KaK) = 180° - 135° + 60° = 105° und die Dreiecksseiten a = Stromgeschwindigkeit und b = FdW.
Wir rechnen also:
Den Wert von cot 52,5° = 0,767 liest man auf D ab und multipliziert mit (-3,5) : 8,5 = -0,412. Den Zahlenwert von cot 52,5° findet man leicht auf der Tangensskala T des Rechenschiebers (von rechts nach links!). Mit dem Rechenschieber geht es in einer Einstellung! Auf der Tangensskala T liest man gleich (α-β)/2 = -17,5°, α-β = -35° ab. Aus der Berechnung von γ wissen wir noch, dass (α+β) = 180° - 105° = 75°. Die Summe der beiden Zahlen liefert 2 · α = -35° + 75° = 40°, α = 20°. Die Differenz liefert 2·β = 110°, β = 55°. Der Kurs muss also um 20° auf 40° geändert werden.
Mit dem Taschenrechner ist es etwas umständlicher, wenn der keine Cot-Funktion hat. Man berechnet tan 52,5° und bildet den Kehrwert. Mit einer Tabellenkalkulation muss man beachten, dass die mit dem Bogenmaß als Argument der trigonometrischen Funktionen rechnet. Man multipliziert daher 52,5° mit π ⁄ 180°.
1. Probe: 20° + 55° + 105° = 180°, die Winkelsumme stimmt. (Diese einfache Probe sollte man immer durchführen!)
Die Geschwindigkeit über Grund (Dreiecksseite c) berechnen wir nach dem Sinussatz:
Mit dem Rechenschieber stellen wir den Läufer über β = 55° auf der Skala S, die Zunge wird so weit verschoben, dass FdW = 6 auf der Skala C unter dem Läuferstrich, also über sin 55°, steht. Nun brauchen wir den Läufer nur noch über γ = 75° auf Skala S zu verschieben, und wir lesen auf der Skala C die FüG = 7,1 kn ab.
2. Probe: Wenn wir den Läufer auf α = 20° auf S verschieben, müßte nach dem Sinussatz ja die SG auf C gefunden werden. Stimmt!
Lösung: Der Kompasskurs muß auf 40° geändert werden, um im Strom 60° über Grund zu fahren, die Geschwindigkeit beträgt 7 kn über Grund.
|
|
© Rainer Stumpe URL: http://www.rainerstumpe.de |