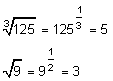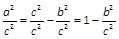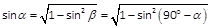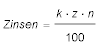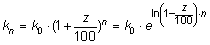Der Rechenschieber
Vorbemerkungen
Ob Rechenschieberrechnen heute noch zu den "Kulturtechniken" gehören soll — darüber lässt sich streiten. Nützlich war er jedenfalls solange es noch keine billigen Taschenrechner gab. Wer mit dem Rechenschieber gerechnet hat, wird ihm nachtrauern, denn Dreisatzaufgaben sind mit keinem Hilfsmittel schneller zu lösen. Rechenschieberrechnen hat zwei wesentliche Vorteile gegenüber dem Taschenrechner:
- man muss die Kommastellen im Kopf abschätzen,
- die Genauigkeit ist begrenzt auf 3 bis 4 signifikante Stellen.
Wer hat sich auf dem Taschenrechner nicht schon beim Dezimalkomma vertippt und es nicht gemerkt? Dem geübte Rechenschieberrechner kann das nicht passieren, denn er hat bereits die Größenordnung des Ergebnisses abgeschätzt. Und spiegelt uns der Taschenrechner mit seinen 8 Anzeigestellen eine nicht vorhandene Genauigkeit vor? Das Ergebnis des Produkts 2,72 · 3,89 ist eben nicht 10,58080, sondern 10,58!
Lust bekommen, den Rechenschieber zu suchen und ihn wieder einzusetzen? Frisch gewagt! Die Übung kommt schneller wieder als man denken sollte (immerhin liegt er seit 20 Jahren in einer Schublade). Auf diesen Seiten gebe ich eine ganz kurze Übersicht, wie man mit ihm rechnet. Ein Anwendungsbeispiel ist die Sportbootnavigation (dazu muss man aber noch ein bisschen Trigonometrie wiederholen). Außerdem habe ich drei Anleitungen meiner Rechenschieber als PDF-Dateien vorbereitet, falls die eigene Anleitung unauffindbar sein sollte.
Die Anleitung für einen interessanten Spezialrechenschieber hat Herr Gerd Ewald zur Verfügung gestellt:
Eine Anleitung für den Faber-Castell Schulrechenstab D52/82 hat Herr Dr.-Ing. Karsten Hansky zur Verfügung gestellt:
Auf zwei Spezialausführungen von Rechenschiebern
- Rechenschieber für Chemiker von Faber-Castell und Nestler,
- Navigational Slide Rule der Firma Unique
gehe ich auf getrennten Seiten ein.
Und so sieht ein Rechenschieber aus (darauf klicken führt zu einem größeren Bild, einen interaktiven hat Arndt Brünner programmiert):
Historische Einführung
Die Vorhersage von Gestirnskonstellationen zur Vorhersage der Zukunft ist wohl ein altes Grundbedürfnis der Menschen. Vermutlich wurde die Trigonometrie zu diesem Zwecke entwickelt. Auf uns sind die Bemühungen der Griechen, die von den Arabern verfeinert worden sind, zum Ende des Mittelalters gekommen. Das Problem waren die Genauigkeit der Vorhersage und der Rechenaufwand. Offensichtlich mussten zum Berechnen Winkelfunktionen und ihre Zahlenwerte ermittelt werden. Hier taten sich Archimedes und seine Zeitgenossen hervor. So richtig in Schwung kamen die Astronomie — und die sphärische Trigonomie — mit der Erfindung des Buchdrucks in Schwung. Es entstanden Tabellenwerke der Sinuswerte (1457) und Rechenvereinfachungsmittel wie die Prosthaphairese (1634).
Der schottische Mathematiker John Napier beschäftigte sich mit der Vereinfachung der Berechnungen (Nepersche Regeln) und er entwickelte Tabellen von Logarithmen der Sinuswerte, wodurch die aufwändige Multiplikation vielstelliger Werte durch eine Addition ersetzt wurde. Inzwischen war bei den Weltumseglungen die Notwendigkeit entstanden, die geografische Breite des Schiffsorts zu bestimmen. Da die verfügbaren Bücher in lateinischer Sprache geschrieben waren, war die Funktion des "Navigators" auf Adlige beschränkt, die die Lateinschule besucht hatten. Als die englische Königin Elisabeth I sich entschloss, Englands Zukunft in der Seefahrt zu suchen, war das Reservoir adeliger Söhne rasch erschöpft. So kommt es, dass Edmund Gunter sein Lehrbuch zur Navigation in englischer Sprache schrieb und am Gresham College Kurse für Navigatoren an bot. Er propagierte logarithmische Skalen und einen Stechzirkel für die Rechnungen — die Funktion des Rechenschiebers.
Der Rechenschieber basiert auf den Logarithmen der natürlichen Zahlen. Die Logarithmen wurden um 1600 unabhängig von Jobst Bürgi und John Napier entwickelt, und 1620 bzw. 1614 publiziert. Henry Briggs schlug die Logarithmen zur Basis 10 vor, die bis zur Verbreitung der Elektronenrechner verwendet wurden, und veröffentlichte 1617 die erste achtstelligen Logarithmentafel der Zahlen bis 1.000 (Briggssche Logarithmen). Dieses Werk wurde 1628 von Adrian Vlacq erweitert auf zehnstellige Logarithmen der Zahlen bis 100.000.
Einen Abdruck der Briggsschen Logarithmentafel (bis 10.000) aus Edmund Gunters Buch "The General Use of the Canon and Tables of Logarithms" biete ich als PDF-Datei an. Dazu gehört die Anleitung (in altertümlicher, englischer Sprache).
Die Logarithmen erlauben einfaches Multiplizieren, Dividieren, Potenzieren und Radizieren (Wurzelziehen) durch Addieren, Subtrahieren, Multiplizieren bzw. Dividieren. Das führte zur ersten Konstruktion eines Rechenhilfsmittels mit logarithmisch geteilten Skalen durch Edmund Gunter, bei dem auf logarithmischen Skalen mit dem Stechzirkel Strecken abgegriffen und addiert bzw. subtrahiert wurden. William Oughtred schlug 1621 gegeneinander verschiebbare Skalen vor, ehe Seth Partridge den modernen Rechenschieber konstruierte, und in seinem Buch The Description and Use of an Instrument called the Double Scale of Proportion. (1685) beschrieb. Zusätzliche Skalen wurden von Max Rietz vorgeschlagen, und als "System Rietz" weit verbreitet. Zunächst wurde der Rechenschieber von Seeleuten und Kaufleuten verwendet. Mit James Watt fand er auch Einzug in das Ingenieurwesen. (Siehe auch Geschichte des Rechenschiebers, Uni Greifswald)
Viele Hintergründe und Informationen bietet die Website der deutschen Rechenschieber-Sammler.
Die höheren Rechenarten
Für das Rechnen mit Zahlen gibt es neben den Grundrechenarten:
- Addieren: 7 + 2 = 9
- Subtrahieren: 7 - 2 = 5
- Multiplizieren: 7 · 2 = 14
- Dividieren: 7 : 2 = 3 ½
Die höheren Rechenarten sind:
- Potenzieren: 72 = 7 · 7 = 49
und seine beiden Umkehrungen
- Radizieren (Wurzelziehen):
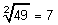
- und Logarithmieren: 10lg(7) = 0,8451.
Der Rechenschieber wird eingesetzt zum Multiplizieren, Dividieren, Potenzieren, Radizieren und Logarithmieren. (Es gibt aber Sonderausgaben, die auf der Rückseite zusätzlich einen "Addiator" für ganz faule anbieten.) Für die Infinitesimalrechnung, die ebenfalls zu den "höheren Rechenarten" gehört, gibt es keine Rechenschieberanwendung — sie stammt aus der analytischen Geometrie.
Rechnen mit Potenzen
Der Potenzausdruck 72 wird gelesen "sieben hoch zwei" oder "sieben zum Quadrat". Er ist die Kurzfassung der Rechenvorschrift: 7 · 7. Der Ausdruck 35 wäre dann die Kurzfassung von 3 · 3 · 3 · 3 · 3 = 243. In diesen Ausdrücken nennt man die auf der Zeile stehende Zahl "Basis", und die hochgestellte "Exponenten". Für das Multiplizieren und Dividieren mit Potenzen gibt es Regeln, falls die Basen oder die Exponenten gleich sind. Potenzen mit ungleichen Base und Exponenten muss man einzeln berechnen. Per definitionem ist 50 = 1 (Jede beliebig große Zahl mit dem Exponenten Null ist gleich 1).
- Gleiche Basis:
- am · an = a(m + n), z. B.
52 · 53 = 5 · 5 · 5 · 5 · 5 = 55 = 3125; - und:
- am : an = a(m - n), z. B.
53 : 52 = (5 · 5 · 5) : (5 · 5) = 51 = 5;.
- am · an = a(m + n), z. B.
- Gleicher Exponent:
- an · bn = (a · b)n, z. B.
33 · 53 = 3 · 3 · 3 · 5 · 5· 5 = 3375 = 153;. - und:
- an : bn = (a : b)n 33 : 53 = (3 · 3 · 3) : (5 · 5 · 5) = 0,216 = (3 : 5)3.
- an · bn = (a · b)n, z. B.
- Negative Exponenten (Bei diesen Rechnungen kânnen negative Exponenten auftreten!):
- a - n = 1 ⁄ an, z. B.
52 : 53 = 5-1 = 1 : 5 = 1 ⁄ 5 = 0,2;.
- a - n = 1 ⁄ an, z. B.
- Potenzen von Potenzen:
- (am)n = a(m · n), z. B.
(52)3 = (5 · 5)3 = (5 · 5) ·(5 · 5) · (5 · 5) = 15625 = 56.
- (am)n = a(m · n), z. B.
1. Umkehrung: Radizieren
Eine der beiden Umkehrungen des Potenzierens ist das Wurzelziehen, symbolisiert mit dem Wurzelzeichen ![]() . Es wird gelesen "dritte Wurzel aus 125". Das Ergebnis ist die Zahl x, deren dritte Potenz 125 ergibt 125 = x3, also x = 5. Vereinbarungsgemäß lässt man die 2 vor dem Wurzelzeichen bei der Quadratwurzel weg:
. Es wird gelesen "dritte Wurzel aus 125". Das Ergebnis ist die Zahl x, deren dritte Potenz 125 ergibt 125 = x3, also x = 5. Vereinbarungsgemäß lässt man die 2 vor dem Wurzelzeichen bei der Quadratwurzel weg: ![]() .
.
In Exponentialschreibweise des Wurzelziehens schreibt man gebrochene Exponenten:
2. Umkehrung: Logarithmieren
Wenn man mit Potenzzahlen zur gleichen Basis das Multiplizieren durch eine Addition der Exponenten ersetzen kann, müsste man nur jede beliebige Zahl durch eine Potenz (zur gleichen Basis) ersetzen und könnte die Multiplikation durch die (manuell) leichtere Addition ersetzen. Das war die Überlegung hinter der Entwicklung der Logarithmen. Die Frage lautet also: Welchen Exponenten m zur Basis 2 hat die Zahl 128, welchen Exponenten n hat die Zahl 512? Dann lässt sich 128 · 512 rechnen als 2(m + n). (Da jede Zahl mit dem Exponenten 0 gleich 1 ist, ist der Logarithmus von 0 unbestimmt.)
- 128 · 512 = 27 · 29 = 216 = 65.536.
Analog den Rechenregeln für Potenzzahlen gilt für Logarithmen:
- log (a · b) = log a + log b
- log (a/b) = log a - log b
Für die Multiplikation bzw. Division der Zahlen a und b (in den Klammern) hat man eine Addition bzw. Subtraktion der Logarithmen der Zahlen a und b erreicht. Vor der Erfindung des Computers war da eine wesentliche Rechenerleichterung. (Wer noch "mit der Hand" multiplzieren und dividieren kann, wird das nachvollziehen.)
Anwendung der Logarithmen
Da man vor der Einführung der elektronischen Rechner die Frage nach dem Logarithmus einer beliebigen Zahl x nur durch eine komplizierte Reihenberechnung — oder wie John Napier durch Berechnen einer geometrischen Reihe — beantworten konnte, wurden Tabellen angelegt, die Logarithmentafeln. In denen wurden alle (positiven) Zahlen x durch die Exponenten 1 zur Basis 10 ausgedrückt x = 101. In Symbolen ausgedrückt log10 x = 1. Der Vorteil dieser quot;dekadischen" Logarithmen (solche zur Basis 10) ist, dass die Logarithmen einstellige Zahlen kleiner sind als 1, die 2-stelliger eine 1 vor dem Komma haben, 3-stellige eine 2, usw. Die Zahl vor dem Komma ist die Kennziffer des Logarithmus.
Um mit 5 signifikanten Stellen rechnen zu kânnen, brauchte man 5-stellige Angaben der Logarithmen (Mantissen). Die Rechnung 128 · 512 mit einer Logarithmentafel sah so aus:
Man suchte die Mantissen von 128 und 512 aus der Tafel heraus und stellte die Zehnerpotenz vor das Komma:
- 128 ⇒ log(128) = 2,10721
- 512 ⇒ log(512) = 2,70927.
- 128 · 512 = log(128) + log(512) = 2,10721 + 2,70927 = 4,81648
Die Logarithmen der beiden Zahlen wurden addiert ⇒ 4,81648. Für die Nachkommazahl (Mantisse) wurde aus der Tafel die zugehârige Zahl herausgesucht 81648 → 65536 und die Ziffer vor dem Komma bestimmte die Zehnerpotenz (100 · 100 = 10.000 = 104), also 128 · 512 = 65.536.
Neben den Logarithmen zur Basis 10 gibt es heute noch die "natürlichen Logarithmen" zur Basis e = 2,7182818284…, der Eulerschen Zahl, verwendet; sie heißen natürliche Logarithmen ln und werden für die Formeldarstellung von Naturgesetzen verwendet. Ihr Vorteil ist, dass z. B. der radioaktive Atomkernzerfall oder das Bakterienwachstum Gesetzmäßigkeiten folgen, die als Potenzen von e gehorchen.
Für das Rechnen mit nur drei oder vier signifikanten Stellen, also für das praktische Leben, reichte die Genauigkeit des Rechenschiebers. Mit ihm addiert und subtrahiert man Strecken geometrisch auf logarithmisch eingeteilten Linealen. Den Logarithmus einer Zahl auf der logarithmischen Skala findet man auf der linearen Skala. log 3 = 0,477.
Man kann nun durch Addieren der Strecken auf der logarithmischen Skala eine Multiplikation ausführen. Dazu benutzt man zwei identische Skalen, die gegeneinander verschiebbar sind.
Das ist das Funktionsprinzip des Rechenschiebers. Die Zehnerpotenzen des Ergebnisses schåtzt man überschlägig ab.
Bauteile und Skalenanordnung
Der zeitgenössische Rechenschieber hatte drei Teile:
- den Körper,
- die Zunge,
- den Läufer.
Auf dem Körper und der Zunge sind die (logarithmischen) Rechenskalen angeordnet; dabei sind zusätzliche Skalen auf der Rückseite der Zunge angeordnet. Der Läufer erleichtert das Einstellen und Ablesen von Zahlenwerten. Zur Handhabung und Pflege des Rechenschiebers gibt die Anleitung zum Schulrechenstab Hinweise.
Der erste von Seth Partridge in seinem Buch "The Description and Use of an Instrument Called the Double Scale of Proportion" beschriebene Rechenschieber bestand aus drei Linealen (die beiden äußeren waren verbunden und bildeten den Körper), auf denen die Skalen eingraviert waren: auf allen drei Teilen die Lines of Numbers, auf dem mittleren die Line of Sines und die Line of Tangents. [Auszug mit seiner Beschreibung des Rechenschiebers]
| Name | Einteilung | Bezeichnung |
|---|---|---|
| logarithmische Skalen | 1 - 10 | Körper: D Zunge: C |
| log. Quadratskalen | 1 - 100 | Körper: A Zunge: B |
| log. Kubikskala | 1 - 1000 | Körper: K |
| inverse log. Skala | 10 - 1 | Zunge: CI |
| Sinus/Cosinus-Skala | 5,5° - 90° | Körper bzw. Zunge: S |
| Tangens/Cotangens-Skala | 5,5° - 45° | Körper bzw. Zunge: T |
| Logarithmusskala | 0 - 1 | Zunge: L |
| Arcus-Skala | 0,55° - 5,5° | Körper: ST |
Man unterscheidet — bezogen auf die Art und Anordnung der Skalen — drei Grundmodelle:
- System Mannheim (nach dem französischen Mathematiker Amédée Mannheim, der um 1850 die erste Standardisierung der Rechenschieber mit transparentem Läufer vorschlug). Diese Rechenschieber sind selten.
- Skalen: C und D, A und B, S und T.
- System Rietz (nach dem deutschen Ingenieur Max Rietz, der 1902 das System Mannheim um die Sinus- und die Tangensskala auf der Rückseite der Zunge einführte).
- System Darmstadt (nach dem Mathematiker an der TU Darmstadt Alwin Oswald Walther, der 1934 die Skalen um die pythagoreischen Skala √(1 - x2) ergänzte und die Sinus- und die Tangensskala auf die Vorderseite des Körpers verlegte. Die Rückseite der Zunge trug drei Exponentialskalen ex trug.)
Die reinen Ausführungen sind alle älter, oder als Werbegeschenke verteilt worden. Daneben waren viele abgeleitete Systeme mit Sonderskalen und abgeleiteten Anordnungen erhältlich, die für Sonderanwendungen (Elektro, Finanzen, Navigation, Chemie u. v. a. m.) optimiert waren.
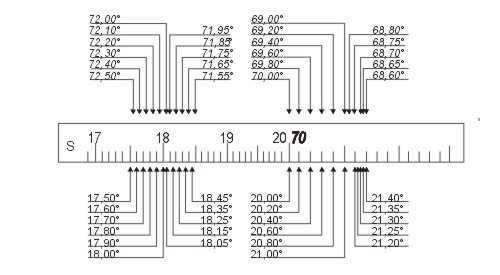
Ablesen der Skalen
Damit man Strecken addieren kann, müssen Skalen, die zum Rechnen dienen, auf Körper und Zunge angeordnet sein. Skalen, die es nur einmal gibt sind nur zum Ablesen von Werten, z. B. der Winkelfunktionen.
Die logarithmische Einteilung der Skalen führt dazu, dass die Strecke zwischen den Zahlen 1 und 2 auf C oder D wesentlich größer ist als die zwischen 9 und 10. Entsprechend kann man im Bereich von Zahlen bis 3 mit mehr signifikanten Stellen rechnen als mit den größeren Zahlen im rechten Teil des Rechenschiebers.
Das gilt auch für die Winkelfunktionsskalen, z. B. für S:
Eine hübsche Anwendung der Quadratskalen A und B ist die Berechnung von Geschwindigkeiten aus Fahrtstrecke (in km oder sm) und Fahrtzeit (in Minuten).
Die pythagoreische Skala P
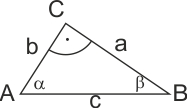
Die pythagoreische Skala P ermöglicht sehr elegant die Stücke des rechtwinkligen Dreiecks zu berechnen, wenn man nur eine Kathete und die Hypotenuse kennt. Nach dem Satz des Pythagoras: a2 + b2 = c2. Löst man diese Gleichung nach einer Kathete auf: a2 = c2 - b2 und dividiert durch c2 erhält man:
Setzt man c = 1 und zieht die Wurzel erhält man:
Da nach der Definition a ⁄ c = sin α und b ⁄ c = sin β ist und im rechtwinkligen Dreieck β = 90° - α gilt, kann man auch schreiben:
Diese Gleichung ist transzendent, d. h. man kann nicht durch Einsetzen einer der Variablen α oder β die andere ausrechnen. Auf eine solche Gleichung ist schon Johannes Kepler gestoßen, als er die Kepler-Gleichung ableitete. Er mußte noch die rechte und die linke Seite der Gleichung ausrechnen und schauen, für welche Wertepaare sie erfüllt ist. Alwin Walther erstellte also eine Tabelle der Werte von √ (1 - cos2 α) mit 0° > α < 90°, und zeichnete sie gleich lang mit der Sinus-Skala auf den Rechenschieber: die pythagoreische Skala war geboren. Ebenso konnte der die gleiche Zahlenreihe mit der C- bzw. der D-Skala des Rechenschiebers in Verbindung bringen.
Bei Rechnungen im rechtwinkligen Dreieck sucht man also den Wert von √(1 - x2) auf der Skala P zum Verhältnis a ⁄ c = sin α, d. h. man teilt die kleinere Zahl durch die größere, und multipliziert diesen mit c; so erhält man die zweite Kathete b. Auf dem Rechenschieber mit geeigneter Skalenanordnung findet man auch die Größe des zwichen a und c eingeschlossenen Winkels β mit einer Einstellung. Der zweite Winkel α folgt aus der Summe der Winkel im rechtwinkligen Dreieck: α + β = 90°.
Es sei a = 18,3 und c = 21,7 so teilt man mit den Skalen C und D 18,3 ⁄ 21,7 = 0,844.
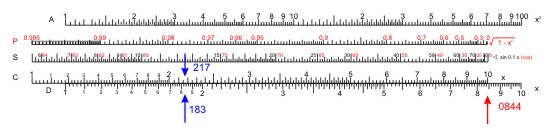
Dann stellt man die Zunge in die Ausgangsstellung und schiebt den Läufer auf 0,844 auf der Skala P. In dieser Einstellung liest man den Winkel β auf der Sinus-Skala S ab: 32,4°. Der zweite Winkel hat die Größe α = 90° - 32,4° = 57,6°.

Nun stellt man die "10" auf der Zungenskala unter den festgehaltenen Läuferstrich und verschiebt den Läufer auf der Skala C über c = 21,7. Unter dem Läuferstrich liest man auf der Skala D das Ergebnis ab: b = 11,63.
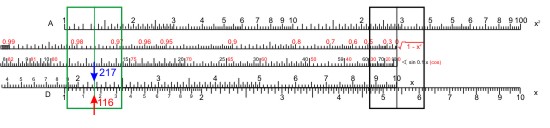
Dieses Verfahren geht wesentlich schneller als das Quadrieren zweier Zahlen, Bilden der Differenz und Wurzelziehen aus dem Ergebnis — aber es funktioniert nur mit dem Rechenschieber. Je nach Anordnung der Skalen auf dem Rechenschieber kann man auch die Winkelfunktionen ebenso bequem zur Berechnung der Grundaufgaben im rechtwinkligen Dreieck verwenden.
Weitere Anwendungen der pythagoreischen Skala sind in diversen Rechenschieberanleitungen. und aus der Seite der Rechenschieber-Sammler.
Die Winkelskalen
Die Logarithmen und der Rechenschieber wurden anfänglich ausschließlich von Kaufleuten und Seefahrern benutzt. Beide haben erheblichen Rechenbedarf: Kaufleute z. B. die Zinsberechnungen, Seeleute Navigationsaufgaben. Für die Navigation gibt es auf dieser Site ausführliche Beispiele — einschließlich der trigonometrischen Grundlagen. In jüngerer Zeit haben besonders Piloten den Rechenschieber für die Berechnung von Kurskorrekturen bei Abdrift durch Seitenwind benutzt. Von Aristo gab es deshalb spezielle Rechenscheiben (Naviat, Aviat) für die Navigation, und in England den Unique Navigator.
Ein hübsches Beispiel zum Rechnen mit trigonometrischen Skalen wird im Kapitel Sphärische Trigonometrie bei der Berechnung der Tageslänge ausgeführt.
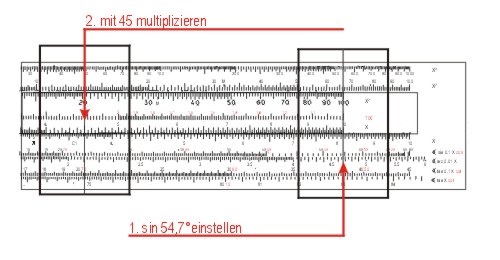
Den üblichen Rechenschieber setzt man aber ein, um Zahlenwerte der Winkelfunktionen abzulesen, oder um aus einer Rechnung den zugehörigen Winkel zu bestimmen. Ein Beispiel ist der Winkel in einem rechtwinkligen Dreieck mit bekannten Seitenlängen (siehe zur Definition der Winkelfunktionen). Den Winkel α zwischen der Ankathete b und der Hypotenuse c mit den Längen 26 cm und 45 cm erhält man aus der Beziehung:
- cos α = Ankathete b : Hypotenuse c = 26 : 45 ⇒ α = 54,7°.
Achtung: Der Cosinus wird auf der Skala S von Rechts nach links abgelesen. Sinus und Cosinus sind ja zyklische Funktionen die Funktionswerte zwischen 0 und 1 annehmen, und die um 90° verschoben sind — genau die Länge der Winkelwerte-Skala auf dem Rechenschieber.
Die Länge der Gegenkathete kann man auf drei Wegen berechnen:
- nach dem Satz des Pythagoras (a2 + b2 = c2)
- sin α = Gegenkathete a : Hypotenuse c ⇒ Gegenkathete = Hypotenuse c · (sin α ),
- mit der pythagoreischen Skala, wenn man einen Rechenschieber des Systems Darmstadt hat.
- Nach dem Pythagoras (a ist die Gegenkathete, c die Hypotenuse) ist die Länge von a:
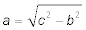 .
.
Die Werte c und b werden nacheinander auf der Skala C eingestellt und auf der Skala B werden die Quadrate abgelesen (hier hilft es die letzte Ziffer zu schätzen, wenn man weiß, dass die Quadrate gerader Zahlen auch gerade sind, und dass die Quadrate von durch 5 teilbaren Zahlen auch eine 5 als letzte Ziffer haben).
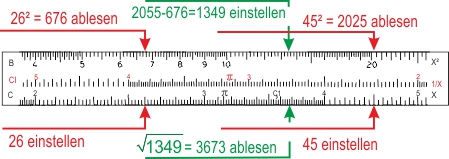
Die Differenz wird manuell gebildet (1349), aber wo soll man sie nun auf B einstellen, bei 1,349 oder bei 13,49? Als Regel gilt: alle ungerad-stelligen (1,3,5...-stellig) Quadratzahlen werden auf der linken, alle gerad-stelligen (2, 4, 6, …-stellig) auf der rechten Hälfte der Skala eingestellt. Auf C liest man dann die Wurzel ab: a = 36,8.
- Mit Winkelfunktionen müssen wir den Sinus von α = 54,7° mit der Hypotenusenlänge c = 45 multiplizieren. Das Ergebnis 36,7 liest man auf D ab.
- Die Berechnung mit der pythagoreischen Skala ist bei der Erläuterung der Skalen des Rechenschiebers ausgeführt.
Die Logarithmusskalen
Neben den Winkelskalen werden wir auch die Logarithmusskalen des Rechenschiebers brauchen (eine Anwendung ist die Zinseszinsrechnung). Verwendet werden die Skalen LL des natürlichen Logarithmus "ln". Da der Logarithmus zur Basis e = 2,71828… (Eulersche Zahl) die Zehnerpotenzen nicht im Kopf berechnen lässt, sind die Skalen LL aufgeteilt und überdecken einen Zahlenbereich von 0,01 bis 105.
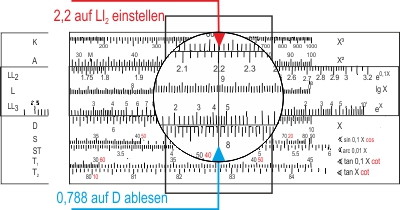
Um den ln 2,2 abzulesen, stellt man den Läufer auf der Skala LL2 über 2,2 und liest auf D den Wert ab: 0,788 (LL2 gibt e0,1x!).
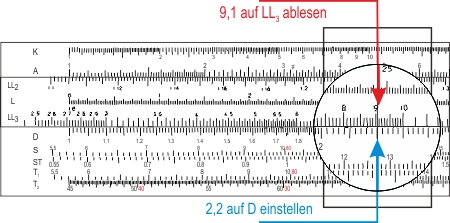
Zum Delogarithmieren, also um ex zu ermitteln, stellt man x = 2,2 auf D ein und liest den Wert der Potenz e2,2 = 9,1 auf LL3 ab.
Beispiel
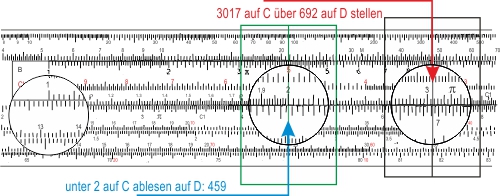
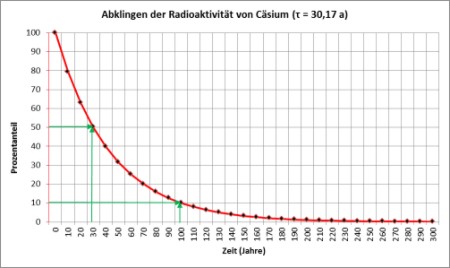
Als Beispiel für die Benutzung der Skalen LL2 und LL3 wollen wir berechnen, um wieviel die radioaktive Strahlung von 137Cäsium nach 20 (und weil's so einfach geht: nach 200) Jahren abgeklungen ist. Dazu verwenden wir die Formel:
Dabei ist die Halbwertszeit τ von 137Cäsium τ = 30,17 a (nach Wikipedia). Zur Berechnung brauchen wir einen Rechenschieber mit ex-Skalen. Auf den wenigsten Rechenschiebern gibt es zusätzliche e-x-Skalen, was nicht schlimm ist. Denn es gilt ja: e-x = 1/ex.
Den Exponenten der Formel berechnen wir zuerst. Und um Arbeit zu sparen in einer Reihenfolge von abwechselnder Multiplikation und Division. Als erstes bestimmen wir den Wert von ln 2.
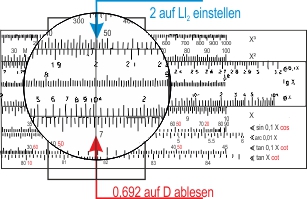
Den Wert "2" finden wir auf der LL2-Skala. Wir schieben den Läufer auf den Wert und lesen auf der Skala D den wert ab: 0,692 (die LL2-Skala liefert e0,1 x Werte).
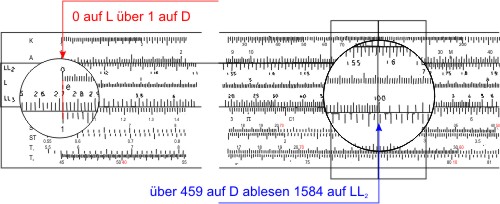
Diesen Wert dividieren wir durch die Halbwertszeit τ 30,17. Dazu muss die Zunge umgedreht werden, damit wir den Wert der Halbwertszeit 3017 auf der Skala C unter dem Läuferstrich einstellen können. Unter der "1" auf der Skala C kânnten wir das Ergebnis ablesen: 0,2298, brauchen wir aber nicht. Zum Multiplizieren mit 20 brauchen wir aber nur den Läufer auf die 2 auf der Skala C zu verschieben und den Zahlenwert des Exponenten auf D abzulesen: 0,459.
Nun müssen wir die Zunge wieder herumdrehen, dass wir die LL2-Skala sehen können. Wir stellen die "0" der L-Skala (dekadischer Logarithmus) über die "1" auf der Skala D, und lesen den Wert von e0,459 auf der LL2-Skala ab: 1,584
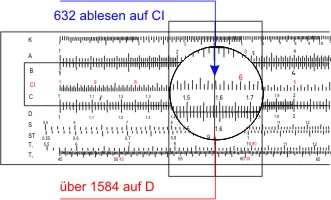
Zum Abschluß brauchen wir nur noch den Kehrwert zu bestimmen. Wir notieren 1,584 und drehen die Zunge wieder zurück. Über der 1,584 auf der Skala D lesen wir den Kehrwert auf der Skala CI (von rechts nach links) ab: 0,632.
Das Ergebnis: nach 20 Jahren (66,3 % der Halbwertszeit) sind noch 63,2 % der ursprünglichen Menge 137Cäsium vorhanden. Und nach 200 Jahren? Dazu brauchen wir in der Einstellung, in der wir den Wert der Exponentialfunktion auf LL2 ablasen nur auf LL3 (ex) abzulesen: 99 und den Kehrwert 0,0101 zu bilden: nach 200 Jahren ist nur noch 1% der ursprünglichen Menge 137Cäsium vorhanden.
Rechnen mit dem Rechenschieber
Mit dem Rechenschieber addiert und subtrahiert man Strecken auf den logarithmisch geteilten Skalen, die auf Körper und Zunge gegenüber liegen. Nach ein wenig Übung muss man nicht mehr nachdenken: es geht "wie von allein".
Multiplizieren
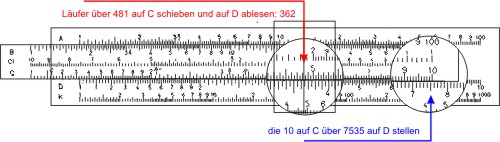
Die Multiplikationsaufgabe 75,35 · 4,81 löst man mit dem Rechenschieber in folgenden Schritten:
Man stellt das Ende der Zungenskala C über die größere Zahl auf der Körperskala D (auf D ist nun die Strecke 7,535 abgegriffen) und schiebt den Läufermittelstrich auf die Zahl 4,81 auf der Zungenskala C. Dadurch ist die Strecke 4,81 abgegriffen. Nun liest man auf D die Länge der addierten Strecken ab: 362. Nun müssen die Kommastellen im Kopf abgeschätzt werden: 70 · 5 ist 350, also lautet das Ergebnis 362.
Dividieren
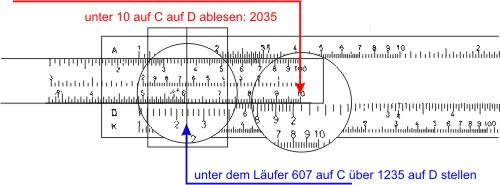
Die Divisionsaufgabe 123,5 : 60,7 löst man durch abziehen zweier Strecken in zwei Schritten:
Wieder werden die Kommastellen im Kopf abgeschätzt: 120 : 60 ist 2 ⇒ das Ergebnis ist 2,035.
Dreisatzaufgaben
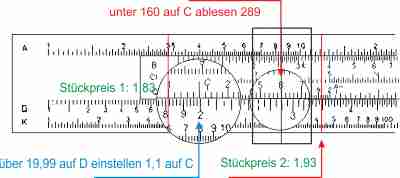
Eine typische Aufgabe des Alltages für den Rechenschieber ist die Dreisatzrechnung oder Proportionalität. Häufig werden Haushaltsprodukte in verschiebenen Packungsgrößen angeboten — die Erfahrung lehrt, nicht immer ist die größere Menge auch die billigste. Von einem Spülmittel gibt es zwei Packungsgrößen: 110 Einheiten zu 19,99 € und 160 Einheiten zu 34,99 €
Man stellt über den Preis (19,99) auf der Körperskala D die Anzahl (110) auf der Zungenskala C, und schiebt den Läufer über die andere Verpackungsgröße (160) auf Skala C. Man liest auf D ab: beim gleichen Stückpreis dürfte die größere Packung nur etwa 29,00 € kosten. Der Stückpreis der größeren Packung liegt bei über 0,193 €. Den Stückpreis der kleineren Packung findet man unter der 1 auf C: 0,182 €.
Andere Verpackungsgrößen vergleicht man durch Verschieben des Läufers.
Ketten rechnen
Mit etwas Übung und Planung kann man Kettenaufgabe mit dem Rechenschieber schnell lösen. Dabei achtet man darauf, dass die Zunge nicht unnötig hin- und hergeschoben wird. Als Regel kann man sich merken: erst dividieren, dann multiplizieren. Eine Kettenaufgabe ist z. B. der Bruch
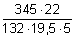 .
.
Zunächst ordnet man die Zahlen so, dass übereinander stehende Paare auf den Rechenschieberskalen C und D möglichst nahe stehen:
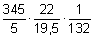 .
.
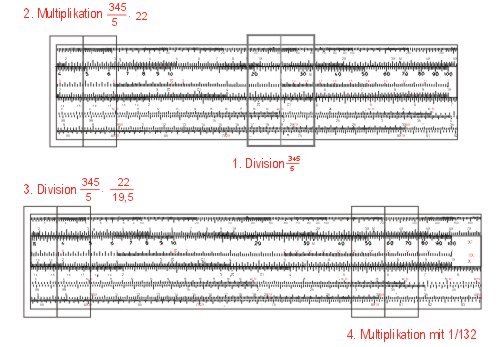
Zuerst stellt man 5 auf C über 345 auf D, verschiebt den Läufer über 22 auf C und verschiebt dann die Zunge, so dass 195 auf C unter dem Läuferstrich steht. Nun kommt der Trick: statt den Läufer auf 10 (C) zu verschieben und 5 auf der Zungenskala C unter den Läuferstrich zu stellen, multipliziert man mit der Skala CI auf der Zunge, d.h. mit 1 ⁄ 132. Dazu bewegt man den Läuferstrich auf 132 der Skala CI. Das Ergebnis 591 liest man auf D ab. Die Kommastelle findet man überschlagsmäßig:
- 300 · 20 = 6000,
- 6000 ⁄ 100 = 60,
- 60 ⁄ 20 = 3,
- 3 ⁄ 5 = 0,6.
- Das Ergebnis der Kettenrechnung ist 0,591.
Rechnung mit den Quadratskalen
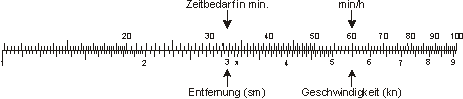
Wenn man eine zurückgelegte Strecke in km oder sm und die für die Fahrt benötigte Zeit in Minuten kennt, gibt es einen hübschen Trick mit dem Rechenschieber: man spart sich eine Multiplikation.
Die Geschwindigkeit v berechnet man durch Division von Weg a und Zeit t : v = a ⁄ t. Man dividiert also die Fahrtstrecke durch die Fahrtzeit — und erhält km ⁄ min oder sm ⁄ min. Das Ergebnis muss man nun mit 60 multiplizieren. Auf den Quadratskalen ( von 1 bis 100) des Rechenschiebers kommt aber eine "60" vor. Also dividieren wir mit den Skalen A und B, und lesen das Ergebnis nicht unter der 1 von A ab, sondern unter der "60": so haben wir gleich mit 60 multipliziert, und brauchen keine Kommastellen abzuschätzen.
Hat unser Segelboot also für 9 ½ Seemeilen 75 Minuten gebraucht, entspricht das eine Geschwindigkeit von 7,6 Knoten.
Will man dagegen wissen, wann man bei einer gegebenen Geschwindigkeit im 3 sm entfernten Hafen ankommt, so stellt man die Geschwindigkeit (5,5 kn) unter die 60 auf A und liest den Zeitbedarf über der Entfernung ab: knapp 33 min.
Zinsrechnung
Bei einer (jährlichen) Verzinsung eines Kapitalbetrages k mit einem Zinssatz z über n Jahre berechnet man Zinsen nach der Zinsformel:
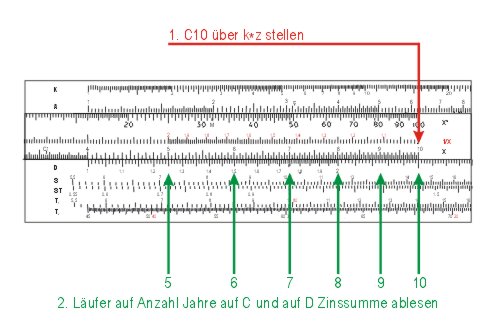
Bei 5.000 €, einem Zinssatz von 5 % und einer Anlage von 6 Jahren erhält man Zinsen in Höhe von 1.500 €. Auf dem Rechenschieber kann man mit der Einstellung k · z gleichzeitig auch den Zinsbetrag für beliebige Jahre ablesen (für 1-3 Jahre muss man die Zunge ´durchschieben).
Zinses-Zinsrechnung
Lässt man die Zinsen stehen, so verzinsen sich die Zinsen ebenfalls: Das Kapital wächst schneller. Die Gleichung für die Kapitalmenge kn nach n = 20 Jahren mit einem Zinssatz z = 12% bei einem Startkapital k0&bvsp;= 100 lautet:
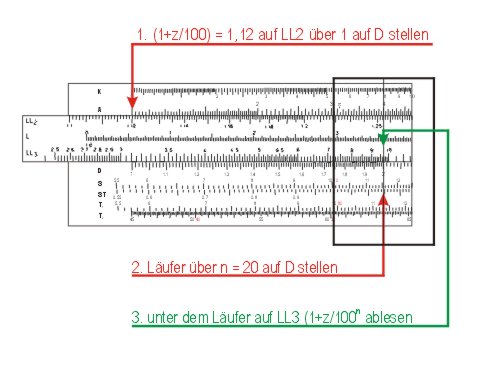
Zunächst berechnet man den Exponentialausdruck (1 + z/100)n, dann schließt sich eine Multiplikation (auf C und D) dieses Faktors mit der Startsumme k0an.
Der Faktor beträgt 9,65, das Kapital von 100 € hat sich nach 20 Jahren auf 965 € verzinst. (das waren noch Zeiten …)
URL: www.rainerstumpe.de/
Datenschutzerklärung