Mechanica sive Motus Scientiae
Caput primum.
De motu non libero in genere.
zur Übersetzung des Abschnitts
Propositio 6.
Problema.
49. Ope penduli efficere ut corpus in data linea moveatur.
zur Übersetzung des Abschnitts
Constructio.
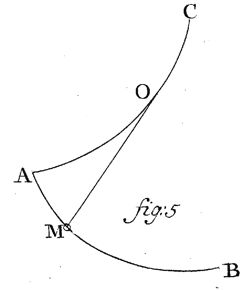
Sit AMB curva proposita in qua corpus moveri debeat; huius curvae construatur evoluta AOC, laminaque secundum eius figuram incurvetur et firmetur. Tum filum huic laminae circumducatur, quod altero termino ad laminam sit affixum, altero vero termino in A annexum habeat corpus movendum. Quando igitur corpus moveri incipit, perspicuum est id in curva AMB moveri debere, quia filum dum a lamina separatur hanc curvam evolutione describit. Q. E. Fac.
Corollarium 1.
50. Hac igitur ratione corpus in data curva progreditur, atque frictionibus non est obnoxium. Quare tali motu commodissime per experimenta effici poterunt, quae in theoria inveniuntur.
Corollarium 2.
zur Übersetzung des Abschnitts
51. Ex doctrina de evolutionibus intelligitur fili partem MO a lamina separatam, in curvam AMB esse normalem ipsumque eius radium osculi.
zur Übersetzung des Abschnitts
Corollarium 3.
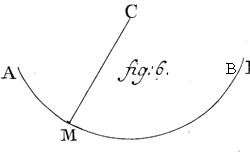
52. Quo corpus in peripheria circuli AMB moveatur, lamina incurvata non est opus, sed filum altero termino C tantummodo in centro C peripheriae est figendum.
zur Übersetzung des Abschnitts
Corollarium 4.
53. Quia filum MO est radius osculi, vis centrifuga tota ad tendendum hoc filum impendetur. Quare hoc filum tum satis roboris habere, tum extensioni obnoxium non esse debet. Nisi enim eandem perpetuo longitudinem conservet, curvam desideratam non describet.
zur Übersetzung des Abschnitts
Corollarium 5.
54. Accedente potentia absoluta, habebitur praeter vim centrifugam vis normalis, quae filum quoque tendet, si vi centrifugae fuerit conspirans. At si contraria fuerit minuet tensionem fili, imo etiam si maior fuerit, comprimet, qua casu evolutio nullius erit usus. Nam cum filum debeat esse flexile, compressioni resistere non poterit, neque ideo impedire, quo minus corpus a curva AMB versus evolutam recedat.
zur Übersetzung des Abschnitts
Scholion 1.
55. Praeter hanc difficultatem, ista curvarum per evolutiones generatio hoc quoque laborat defectu, quod linea recta produci nequeat; ad eam enim generandam filum requireretur infinite longum. Simili modo haec evolutio ad curvas accommodari non potest, quae alicubi radium osculi habent infinite magnum. Deinde etiam neque cuspide neque flexu contrario praeditae curvae hoc modo describi possunt. Quamobrem ita praxis locum tantum habet in curvis ubique finitam curvaturam habentibus, ad quod addi debet, ut pressio curvae totalis nusquam in curvae concavam partem dirigatur.
zur Übersetzung des Abschnitts
Scholion 2.
56. Hugenius, qui primus evolutionis doctrinam excoluit, statim eam ad hunc ipsum usum adhibuit; uti ex eius egregio opere de horologio oscillatorio apparet. Cum enim invenisset oscillationes super cycloide omnes esse isochronas, motum super cycloide in horologia inferre volebat, quod per pendulum intra cycloides oscillans effecit. Cum enim cycloidis evoluta sit cyclois, hac ratione obtinuit, ut corpus filo annexum in cycloide moveretur.
zur Übersetzung des Abschnitts
Scholion 3.
57. In hoc autem pendulorum motu maxime notari convenit, praeter corpus motum filum quoque moveri debere, id quod ad institutum huius libri, in quo de motu puncti tantum agetur, minime pertinet. Praeterea motus corporis pendulo annexi non est sibi parallelus, sed circularis circa centrum scilicet circuli curvam osculantis, qui motus pariter hoc loco non attingitur. Hoc igitur libro motum puncti duntaxat super linea vel superficie data examini subiiciemus, mentemque tam a motu fili, quam a motu circulari abstrahemus. In sequentibus autem motum pendulorum, ubi et motus fili et motus circularis in computum ducetur, ad motum puncti tantum reducemus, ita ut haec, quae hoc libro tractabuntur, nihilominus in praxi usum sint habitura. Quamobrem, ut iam monuimus, punctum motu sibi semper parallelo super curva seu superficie sine ulla frictione ferri est concipiendum.
zur Übersetzung des Abschnitts
…
Caput Secundum.
De motu puncti super data linea in vacuo.
Propositio 12.
Problema.
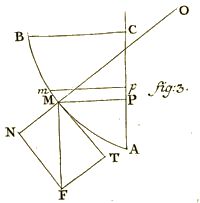
83. Sollicitetur corpus, quod super curva AM movetur, ubique a potentia MF cuius directio sit parallela axi AP; determinare celeritatem corporis in singulis punctis, atque tempus, quo curvae quaevis portio describitur, nec non pressionem, quam curva in singulis punctis patitur.
zur Übersetzung des Abschnitts
…
Propositio 13.
Problema.
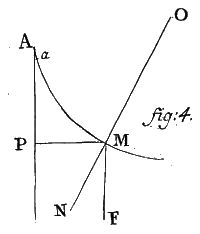
93. Si potentia sollicitam fuerit uniformis et ubique deorsum tendat, determinare descensum corporis super data curva AM in A ex quiete incipientem, atque pressionem, quam curva, in singulis punctis M sustinet.
zur Übersetzung des Abschnitts
…
Corollarium 7.
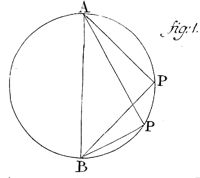
102. Ex hoc perspicitur in circulo APPB omnes descensus per chordas AP ex puncto supremo A ductas, nec non omnes descensus per chordas ad punctum infimum B ductas aequalibus fieri temporibus; eo scilicet tempore, quo corpus per diametrum AB perpendiculariter delabitur.
zur Übersetzung des Abschnitts
…
Propositio 14.
Problema.
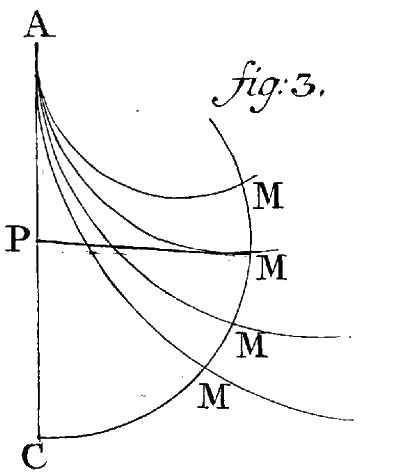
106. Si fuerint infinitae curvae similes AM, AM etc. ex puncto fixo A initium sumentes; invenire curvam CMM, ab illis curvis arcus AM, AM etc. abscindentem, qui a descendente super iis corpore aequalibus temporibus percurrantur; existente ut ante potentia sollicitante uniformi et ubique deorsum directa.
zur Übersetzung des Abschnitts
Solutio.
Ex infinitis curvis datis sumatur una quaecunque AM, cuius parameter sit a. Positoque AP = x, et arcu AM = s et existente ut ante potentia sollicitante = g, descendat corpus super curva AM, erit celeritas in M debita altitudini gx. Tempus ergo descensus super AM erit = 
. Ab omnibus ergo curvis AM, AM etc. tanti arcus sunt abscindendi, ut pro iis sit quantitas constans. At ad alias curvas referetur, si praeter s et x etiam parameter a ponatur variabilis. Posito igitur in 
etiam a variabili, quantitas ponenda est constanti, nempe ei tempori quo omnes; descensus fieri debent. Sit hoc tempus = k erit k = in singulis curvis. Quare si ita differentietur ut etiam a variabile ponatur, hoc differentiale nihilo aequale est ponendum. Ad hoc differentiale inveniendum sit ds = pdx, eritque p, quia omnes curvae ponuntur similes, functio in qua a et x nullum dimensionum numerum simul constituunt. Habebimus ergo hoc differentiatum posito quoque a variabili dabit 
quod fieri debet = 0. Quantitas q vero sequenti modo invenietur. Quia est k = 
; in quantitate k, variabiles a et x dimensionum numerum constituent ½. Ostendi autem alibi in Tom. IX. Comment. tum fore 
. Ex quo invenitur 
. Habebitur ergo 
. Quae est aequatio pro curva quaesita. At si aequatio inter coordinatas x et y pro curva CMM desideretur, ex aequatione pro quaque curvarum AM, valor ipsius a in x et y inventus substitui debet. Q. E. I.
zur Übersetzung des Abschnitts
Corollarium 1.
107. Aequatio etiam primo inventa 
sufficit ad curvam CMM inveniendam. Nam pro quavis abscissa AP = x ex ea invenitur a parameter eius curvae AM, cuius punctum M respondens assumtae abscissae x est in curva quaesita CMM.
zur Übersetzung des Abschnitts
Corollarium 2.
108. Cum autem haec aequatio sit differentialis, ideoque ad plures curvas pro constante quae adiicitur, pertineat; notandum est in additione constantis, eam tantum solutioni esse convenientem, quae pro data curva seu pro dato ipsius a valore det abscissam x tantum arcum AM abscindentem, qui tempore k descensu absolvatur.
zur Übersetzung des Abschnitts
Corollarium 3.
109. Si tempus k aequale esse debeat tempori descensus per verticalem AC = b, erit k = 
. Quo valore substituto habebitur aequatio 
. In cuius integratione id est faciendum, ut curva per punctum C transeat.
zur Übersetzung des Abschnitts
vScholion 1.
110. Erit autem semper recta verticalis AC species curvarum AM; quae oritur, si parameter a vel infinite magna vel infinite parva accipiatur. Quare commodissime tempus constans k per descensum per verticalem AC, quippe speciem curvarum AM, exprimitur. Atque in constructione aequationis inventae 
tanta constans est addenda, ut posito x = b, fiat a vel infinitum vel nihil, prout ille vel iste valor ipsius a recta AC respondeat.
zur Übersetzung des Abschnitts
Scholion 2.
111. Si 
reipsa potest integrari, ne data quidem aequatione opus est, ad quam inveniendam opus fuit q determinare. Nam si integrale ipsius iterum differentietur posito quoque a variabili reipsa obtinetur q; atque hoc differentiale tantum nihilo aequale esset ponendum. Commodissime vero his casibus problema solvetur, si integrale ipsius statim ipsi k vel 
aequale ponatur, et loco a eius valor in x et y substituatur ex aequatione pro curvis datis. Atque hoc modo solutio in promtu est non solum pro curvis similibus, sed dissimilibus etiam, si modo tempora descensus per quantitates finitas exprimi possunt.
zur Übersetzung des Abschnitts
Exemplum 1.
112. Si omnes hae curvae AM fuerint rectae diversimode ad verticalem AC inclinatae, erit y = nx et 
ubi n tanquam parameter est consideranda. Erit ergo 
quod aequale poni debet ipsi 
. Erit itaque x (1 + n2) = b. Cum autem n sit quantitas variabilis, ponatur pro ea valor y ⁄ x ex aequatione y = nx: quo facto prodibit pro curva CMM aequatio inter coordinatas orthogonales x et y ista y2 + x2 = bx, quae est pro circulo, cuius diameter est recta AC = b.
zur Übersetzung des Abschnitts
Scholion 3.
113. Hic casus est ille ipse casus ante pertractatus (102), ibi enim ostensum est corpus per omnes chordas in circulo ex puncto supremo eductas aequalibus temporibus descendere. Pertinet hic quidem casus non ad curvas similes; sed hoc exemplum attulimus ad casum Scholii 2. illustrandum, quia pro rectis hisce tempora descensus finitis quantitatibus exprimuntur. Sequentia exempla vero curvas similes, uti propositio postulat, complectentur.
zur Übersetzung des Abschnitts
Exemplum 2.
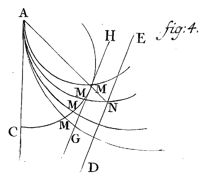
114. Sint curvae AM, AM omnes circuli tangentes verticalem AC in A. Ponatur radius cuiusque eorum =a, erit 
atque 
. Hi circuli vero omnes sunt curvae similes, quia a, y et x in aequatione eundem dimensionum numerum tenent, seu homogeneitatem complent sola. Radius igitur a tanquam parameter variabilis debet tractari. Habetur autem ex illa aequatione 
, quare erit 
, ideoque praescriptam habet proprietatem, ut a et x dimensionum numerus sit nullus. Hanc ob rem pro curva CMM haec habebitur aequatio 
, seu haec 
. Quae aequatio construi potest, posito enim x = au, prodit 
in qua indeterminatae sunt a se invicem separatae. Quo autem aequatio inter coordinatas x et y pro curva CMM obtineatur, ponatur loco a valor 
et loco da eius differentiale 
. Quibus substitutis sequens prodit aequatio differentialis 
. Quae ita integrari debet ut posito x = b fiat y = 0, quia curva per punctum C transire debet.
zur Übersetzung des Abschnitts
Corollarium 4.
115. Ex hac aequatione tangens curvae CMM in singulis punctis cognoscitur, et ex positione tangentis innotescit angulus AMM, quo curva CMM quamlibet datarum intersecat. Erit scilicet tangens anguli AMM = 
. Hic ergo angulus est rectus in C, ob x=b, seu curva CMM in C ad AC est normalis.
zur Übersetzung des Abschnitts
Corollarium 5.
116. Si b vel maior vel minor accipiatur curva CMM alia quoque erit, hocque modo infinitae orientur curvae a circulis arcus isochronos abscindentes. Haeque curvae omnes inter se erunt similes, ob parametrum b, quae in aequatione cum x et y homogeneitatem constituit. Data ergo una curva CMM innumerabiles aliae ex ea construi possunt, abscissis scilicet et applicatis curvae CMM in eadem ratione augendis vel diminuendis, in qua AC seu b augetur vel diminuitur.
zur Übersetzung des Abschnitts
Exemplum 3.
117. Sint curvae AM, AM omnes cycloides cuspides in A habentes et tangentes verticalem AC in A. Posita parametro cuiusque cycloidis AM seu dupla diametro circuli generatoris = a; erit ex natura cycloidis 
atque 
; hincque 
. Hoc ergo casu est 
, functio ipsarum a et x nullius dimensionis ut requiritur. Quare pro curva CMM reperitur ista aequatio 
seu 
. Si aequatio inter coordinatas orthogonales x et y desideretur, ex aequatione 
seu huius differentiali posita quoque a variabili, valor ipsius a debet substitui. Haec vero aequatio differentiata posito a quoque variabili dat 
seu 
. Quae abit in hanc 
. Superior vero per 
multiplicata praebet hanc, 
. Hae duae aequationes additae dant aequationem integrabilem, cuius integralis est 
. Ex qua valor ipsius a erutus fit 
et 
. Quibus valoribus in aequatione 
, quae oritur ex duabus differentialibus eliminato da, substitutis prodibit 
aequatio pro curva quaesita CMM.
zur Übersetzung des Abschnitts
Corollarium 6.
118. Ex hac aequatione invenitur tangens anguli, quem curva CM cum applicata PM constituit nempe 
. Deinde etiam innotescit tangens anguli, quem cyclois AM cum applicata PM constituit. Ex aequatione cycloidis erit nimirum 
. Eliminato vero a erit ista tangens = 
. Quare cum horum angulorum alter alterius sit complementum, sumto illius deinceps posito, erit angulus, quem curva CMM cum qualibet datarum AM constituit, rectus. Consequenter curva CMM est traiectoria orthogonalis omnium cycloidum datarum AM, AM &c.
zur Übersetzung des Abschnitts
Corollarium 7.
119. Sumto AC alius magnitudinis, aliae quoque curvae CMM prodibunt, et sic infinitae traiectoriae orthogonales inveniuntur, quae omnes inter se sunt similes. Data ergo una facile quotquot libuerit, construere licebit.
zur Übersetzung des Abschnitts
Scholion 4.
120. Omnes hae curvae arcus abscindentes isochronos, quaecunque fuerint curvae secandae, semper construi possunt, etiamsi id ex aequatione non appareat. Per quadraturas enim ex datis curvis arcus possunt abscindi, qui dato tempore descensu absolvantur, hocque modo puncta quotlibet curvae quaesitae inveniuntur. Si quidem curvae secandae sunt algebraicae, aequatio pro curva secante semper ita est comparata, ut factis debitis substitutionibus indeterminatae a se invicem possint separari. At si curvae secandae differentiali aequatione exprimantur, aequatio differentialis pro curva secante rarissime separationem indeterminatarum admittit. Causa est, quod peculiari modo, quo in hoc cycloidum casu usus sum, parameter a eliminari debeat; eaque substitutio ad separationem non deducat.
zur Übersetzung des Abschnitts
Scholion 5.
121. Deinde observandum est, omnes curvas arcus isochronos abscindentes, quarum numerus pro vario ipsius b valore est infinitus, inter se similes esse, si quidem curvae secandae fuerint tales. Colligitur hoc ex generali aequatione 
in qua cum p sit functio ipsarum a et x nullius dimensionis quantitates a, b et x homogeneitatem constituunt. At ex aequatione curvarum secundarum, quia in ea a, x et y ubique eundem dimensionum numerum conficere ponuntur, valor ipsius a erit functio ipsarum x et y unius dimensionis. Quare eo substituto loco a habebitur aequatio pro curva secante, in qua b, x et y ubique eundem dimensionum numerum constituunt. Consequenter b variabili posito oriuntur infinitae curvae similes inter se respectu puncti A. Data ergo unica, reliquae facile ex similitudinis ratione describuntur.
zur Übersetzung des Abschnitts
Scholion 6.
122. Materia haec de arcubus isochronis abscindendis iam praeterito seculo est pertractata in Act. Erud. Lips. A. 1697. a Cel. Ioh. Bernullio, atque postmodum in Comment. Acad. Paris. a Cel. Saurino, qui vero alia methodo sunt usi. Ego vero eam adhibui methodum, quam in nostris Comment. pro A. 1734. tradidi, tanquam commodissimam ad huiusmodi problemata solvenda. In his vero locis Viri Cel. curvas quoque similes tantum, ut ego, consideraverunt, sine dubio, quia pro curvis dissimilibus solutio sit nimis difficilis et saepe etiam vires superat. Vocantur vero in locis citatis hae curvae synchronae, quia arcus simul percursi abscinduntur.
zur Übersetzung des Abschnitts
Scholion 7.
123. Ex mea dissertatione Tomi IX. Comment. Acad. Petrop. [Commentarii Academiae Scientiarum Imperialis Petropolotanae, Tom. IX, 1764, S. 3 ff] apparet, has curvas synchronas simili modo posse inveniri, si curvae datae etiam non fuerint similes, sed eiusmodi tamen, ut posito ds = pdx, in p quantitates a et x datum dimensionum numerum constituant; tum enim aeque facile valor literae q invenitur. Ut si numerus dimensionum ipsarum a et x in p fuerit n, aequatio pro curva secante reperietur haec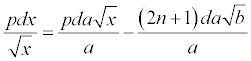 
. Quare si fuerit n = -½, ut si fuerit 
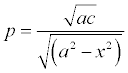, erit 
ideoque x = ma, seu x in data ratione ad parametrum a est capiendum: quo igitur casu constructio synchronarum est facillima. At si p non huiusmodi habuerit valorem, ex supra citata dissertatione mea intelligitur, quo modo in aequationem quaesitam sit inquirendum.
zur Übersetzung des Abschnitts
Mechanik oder die Wissenschaften der Bewegung.
Erstes Kapitel.
Über die Art der nicht freien Bewegung.
These 6.
Fragestellung.
49. Mit Hilfe des Pendels zu bewirken, dass der Körper in einer vorgegebenen Linie bewegt wird.
Aufbau.
Es sei AMB die vorgeschlagene Kurve, in der der Körper bewegt werden muss; dessen Kurve werde konstruiert aus der Evolute AOC und gemäß dem Blech dessen Gestalt gekrümmt und befestigt wird. Ferner wird der Faden um dieses Blech herumgeführt, welcher am einen Ende an dem Blech befestigt ist, aber am anderen Ende in A den zu bewegenden Körper angebunden hat. Wann also der Körper beginnt sich zu bewegen, ist offenbar, dass dieser in der Kurve AMB bewegt werden muss, weil der Faden, sobald er vom Blech getrennt wird, diese Kurve durch Evolute beschreiben wird. Was zu machen war.
1. zusätzliche Erklärung.
50. Mit dieser Überlegung schreitet der Körper auf der gegebenen Kurve fort, und zwar nicht behindert von Reibungen. Weshalb eine solche Bewegung aus den Experimenten bewiesen werden konnten, die in der Theorie gefunden werden.
2. zusätzliche Erklärung.
51. Aus der Lehre über die Evoluten wird der Teil MO des vom Blech getrennten Fadens verstanden, dass er auf der Kurve AMB, die die Normallinie und deren Radius selbst berührt.
3. zusätzliche Erklärung.
52. Wodurch der Körper auf dem Umfang des Kreises AMB bewegt wird, das gekrümmte Blech braucht man nicht, aber den Faden, der am anderen Ende C lediglich im Mittelpunkt C des Umfangs befestigt ist.
4. zusätzliche Erklärung.
53. Weil der Faden MO der Radius der Berührung ist, wird die gesamte Zentrifugalkraft zum Spannen dieses Fadens aufgewandt. Weshalb dieser Faden bald einen ausreichenden Stützpunkt hat, bald der Ausdehnung kein Hindernis sein muss. Denn nur wenn dieser eine unendliche Länge erhielte, würde er die gewünschte Kurve nicht beschreiben.
5. zusätzliche Erklärung.
54. Zur vollständigen Möglichkeit gehört, wird außer der Zentrifugalkraft die Normalkraft gehalten werden, die den Faden auch spannt, wenn sie mit der Zentrifugalkraft zusammenwirkt. Aber wenn sie entgegenwirkt, verringert sie die Spannung des Fadens, wenn sie auch größer sein wird, in welchem Falle die Evolution keinen Nutzen haben wird. Denn weil der Faden biegsam sein muss, kann er dem Zusammenpressen nicht widerstehen, auch deswegen nicht festhalten, umso weniger würde der Körper von der Kurve AMB zur Evolute zurückgehen.
1. Erläuterung.
55. Außer dieser Schwierigkeit, diese Erzeugung der Kurven durch Evoluten erzeugt diesen auch durch den Abfall, was keine gerade Linie erzeugen könnte; denn dazu wäre ein unendlich langer Faden notwendig. Auf ähnliche Weise kann diese Entwicklung zu Kurven nicht eingerichtet werden, welche irgendwo einen unendlich großen Radius der Berührung haben. Hierauf können auch die Kurven versehen weder mit einer Spitze noch einer entgegengesetzten Biegung auf diese Weise beschrieben werden. Deshalb hat so die Handhabung in den Kurven, die überall einen solchen Ort endlicher Krümmung haben, an den zugefügt werden muss, damit der vollständige Druck der Kurve nirgends in der Kurve einen gewölbten Teil gelenkt wird.
2. Erläuterung.
56. Christiaan Huygens, der als Erster die Lehre der Evolution ausgearbeitet hat, hat diese sogleich zu diesem Nutzen selbst angewandt; wie es aus dessen ausgezeichnetem Werk über die Pendeluhr scheint. Denn weil er gefunden hatte, dass alle Schwingungen über der Zykloide isochron sind, wollte er die Bewegung über der Zykloide in die Uhr hineintragen, was er durch den innerhalb der Zykloide schwingenden Pendel gemacht hat. Denn weil die abgerollte Zykloide eine Rollkurve sei, hat er diese Erklärung erhalten, dass der an einem Faden befestigte Körper auf einer Zykloide bewegt wird.
3. Erläuterung.
57. Bei dieser Bewegung der Pendel passt aber besonders zusammen dass beobachtet wird, außerdem muss der bewegte Körper auch den Faden bewegen, dies was er beim Vorhaben seines Buches, in dem die Bewegung des Punktes so viel behandelt wird, keineswegs betrifft. Außerdem ist die Bewegung des am Pendel befestigten Körpers nicht zu sich parallel, sondern selbstverständlich eine kreisförmig schwingende Kurve um den Mittelpunkt des Kreises, welche Bewegung an dieser Stelle eben so nicht berührt wird. Wir werden in diesem Buch deshalb die Bewegung des Punktes über mehr oder weniger einer gegebenen Linie oder Oberfläche einer Prüfung unterziehen, und wir werden die Überlegung so durch die Bewegung des Fadens wie durch die Kreisbewegung ableiten. In den folgenden aber wird die Bewegung der Pendel, wenn sowohl die Bewegung des Fadens als auch die Kreisbewegung in die Betrachtung einbezogen wird, wir werden auf die Bewegung eines solchen Punktes zurückführen, so dass diese, in diesem Buch behandelt werden, nichtsdestoweniger werden sie in der Behandlung von Nutzen sein. Deshalb, damit wir nun erinnert haben, man muss sich vorstellen, dass der Punkt durch die immer zu sich parallele Bewegung über der Kurve oder der Oberfläche ohne jede Reibung getragen wird.
Zweites Kapitel.
Über Bewegung des Punktes auf eine gegebenen Linie im Vakuum.
These 12.
Fragestellung
83. Der Körper werde angestoßen, der über die Kurve AM bewegt wird, sei dessen Potential MF überall in Richtung parallel zur Achse AP; zu bestimmen ist die Geschwindigkeit des Körpers in den einzelnen Punkten, oder die Zeit, die in einem beliebigen Teil der Kurve beschrieben wird, und auch der Druck, den die Kurve im einzelnen Punkt aushält.
These 13.
Fragestellung
93. Wenn die Kraft einheitlich gewirkt haben wird und überall nach unten gerichtet zieht, ist zu bestimmen der Abstieg des Körpers über die gegebene Kurve AM im Punkt A aus der Ruhe beginnend, oder der Druck, den die Kurve, in einzelnen Punkten M trägt.
7. zusätzliche Erklärung.
102. Daraus wird erkannt, dass im Kreis APPB jeder Abstieg durch die Sehnen AP aus dem obersten Punkt A gezogen, und auch jeder Abstieg über die Sehnen vom untersten Punkt nach B gezogen gleiche Zeiten sein werden; selbstverständlich fällt der Körper in der Zeit senkrecht über den Durchmesser AB.
These 14.
Fragestellung
106. Wenn es unendliche ähnliche Kurven AM, AM, u.s.w. die anfänglich aus einem festen Punkt A angenommen gäb; es ist die Kurve CMM zu finden, die den Bogen von jenen Kurven AM, AM u.s.w. abschneiden, der vom über ihnen absteigenden Körper zu gleichen Zeiten durchlaufen wird; die folgend wie vor der einheitlichen und überall abwärts gerichteten Wirkkraft.
Lösung.
Aus den unendlichen gegebenen Kurven wird irgendeine AM gewählt, deren Parameter sei a. Und für AP = x gesetzte, und für den Bogen AM = s und es wird dass vor die Wirkkraft = g, steigt der Körper über die Kurve AM ab, wird die Geschwindigkeit in M ab durch die Höhe gx bestimmt. Also wird die Zeit des Abstiegs in M = sein. Von allen Kurven AM, AM sind also so große Bögen abszuschneiden, dass für diese eine konstante Größe sei. Aber bezieht sich auf andere Kurven, wenn außer s und x auch der Parameter a variabel gesetzt wird. Auch die Variable a in eingesetzt also, die Größe ist konstant zu setzen, nämlich diese Zeit von allen; müssen den Abstieg machen. Diese Zeit sei k es wird k = in den einzelnen Kurven sein. Deshalb wird wenn so differentiert wird, dass auch a variabel gesetzt wird, dieses Differential nichts gleichzugesetzen sein. Um dieses Differential zu finden sei ds = pdx, und es wird p sein, weil alle Kurven ähnlich gesetzt werden, die Funktion in der a und x zugelich keine Zahl der Dimensionen darstellen. Wir werden also diese differenziert und auch die Variable a eingesetzt wird ergeben, was = 0 gemacht werden muss. Die Größe q aber wird nach dem folgenden Verfahren gefunden. Weil k = ist; in der Größe k werden die Variablen a und x die Zahl der Dimensionen ½ bedeuten. Ich habe aber anderswo im Band IX der Erläuterung (Commentationes analyticae ad calculum variationum pertinentes) ferner gezeigt es ist . Daraus wird gefunden . Also hat man . Das ist die Gleichung für die gesuchte Kurve. Aber wenn die Gleichung in den Koordinaten x und y für die Kurve CMM gesucht wird, aus der Gleichung für jede Kurve AM, muss der Wert von a in x uns y gefunden und eingesetzt werden. Was zu finden war.
1. zusätzliche Erklärung.
107. Die zuerst gefundene Gleichung ist auch hinreichend zum Finden der Kurve CMM. Denn für jede beliebige Abszisse AP = x aus der der Parameter der Kurve AM gefunden wird, deren Punkt M entspricht der angenommenen Abszisse x liegt auf der gesuchten Kurve CMM.
2. zusätzliche Erklärung.
108. Weil aber diese Gleichung differenziell ist, daher trifft sie auf mehrere Kurven zu, denen eine Konstante zugefügt wird; es ist bei der Addition der Konstanten zu beachten, dass diese sehr passend ist für die Lösung, die für die gegebene Kurve oder für den gegebenen Wert von a die Abszisse x gibt, der den so großen Bogen AM abschneidet, der in der Zeit k beim Abstieg vollendet wird.
3. zusätzliche Erklärung.
109. Wenn die Zeit k gleich sein soll zur Zeit des Abstiegs durch die Vertikale AC = b, wird k = sein. Durch den eingesetzten Wert werden wir dir Gleichung haben. Mit deren Intergration kann erreicht werden, dass die Kurve durch den Punkt C geht.
1. Erläuterung.
110. Es wird immer eine Art gerade vertikale AC geben der Kurven AM; die entsteht, wenn der Parameter a entweder unbegrenzt groß oder unbegrenzt klein angenommen wird. Deshalb wird am passendsten die Konstante k für den Abstieg durch die Vertikale AC, natürlich die Art der Kurven AM, ausgedrückt. Sowie wird bei der Konstruktion der gefundenen Formel die so große Konstante hinzugefügt, dass eingesetzt x = b, a entweder unbegrenzt oder Null wird, sowie jene oder der Wert von q der Geraden AC entspricht.
2. Erläuterung.
111. Wenn wirklich integriert werden kann. Denn wenn das Integral selbst wiederum differenziert wird auch die Variable a eingesetzt wird selbstverständlich q erhalten. Aber in diesem Falle wird die Fragestellung bequem gelöst, wenn das Integral selbst sogleich k selbst oder gleich gesetzt wird, und an Stelle von a dessen Wert in x und y eingesetzt wird aus der Gleichung für die gegebenen Kurven. Und auf diese Weise ist die Lösung offensichtlich, nicht nur für ähnliche Kurven, sondern auch für unähnliche, wenn nur die Zeiten des Abstiegs durch endliche Größen ausgedrückt werden können.
1. Beispiel
112. Wenn alle diese rechten Kurven AM in unterschiedlichem Grad zur Vertikalen AC geneigt wären, wird y = nx und wobei n gleich wie ein Parameter zu berücksichtigen ist. Also wird gelten, dass was gleichgesetzt werden muss zu . Daher wird x(x + n2 = b. Weil aber n eine variable Größe ist, wird dafür der Wert y ⁄ x aus der Gleichung y = nx gesetzt: durch welche Tat wird für die Kurve CMM die Gleichung in den orthogonalen Koordinaten x und y hervorgehen diese ist y2 + x2 = bx, die für den Kreis gilt dessen Durchmesser ist genau AC = b.
3. Erläuterung.
113. Dieser Fall ist jener Fall, der vorher behandelt wurde (102), denn dort ist gezeigt worden, dass der Körper über alle Sehnen im Kreis, die von dem obersten Punkt gezogen wurden, zu gleichen Zeiten herabsteigt. Dieser Fall betrifft allerdings nicht die ähnlichen Kurven; aber wir haben dieses Beispiel zum Fall der Erklärung 2 hinzugefügt, um zu erklären, weil für diese Geraden die Zeiten des Abstiegs durch begrenzte Größen ausgedrückt werden. Die folgenden Beispiele aber werden ähnliche Kurven einschließen, wie die Vorstellung es fordert.
2. Beispiel
114. Es seien die Kurven AM, AM alle Kreise, die die Vertikale AC in A berühren. Der Radius irgendeiner dieser wird = a gesetz, das ergibt oder . Diese Kreise sind aber alles ähnliche Kurven, weil a, y und x in der Gleichung dieselbe Anzahl Dimensionen halten, oder die Einheitlichkeit allein erfüllen. Deshalb muss der Radius eigentlich wie ein variabler Parameter behandelt werden. Aber man erhält aus jener Gleichung daher wird , und deswegen hat sie die vorgeschriebene Eigenschaft, wenn a und x die Größe der Nummer Null ist. Diese hat deswegen für die Kurve CMM diese Gleichung , oder diese . Welche Gleichung aufgestellt werden kann, den x = au, ergint in der die Unbestimmten getrennt sind von einander. Wodurch aber die Gleichung in den Koordinaten x und y für die Kurve CMM erhalten würde, an Stelle von a würde der Wert und an Stelle von da deren Differenzial . Aus dieser Substitution entsteht die Differenzialgleichung . Diese wird so integriert, dass ersetzt man x = b y = 0 wird, weil die Kurve durch den Punkt C gehen muss.
4. zusätzliche Erklärung.
115. Aus dieser Gleichung wird die Berührung der Kurve CMM in einzelnen Punkten erkannt, und aus der Lage der Tangente wird der Winkel AMM klar, welchen der gegebenen die beliebige Kurve CMM schneidet. Der Berührungswinkel wird selbstverständlich AMM = sein. Also ist dieser Winkel rechtwinklig in C, wegen x = b, oder die Kurve CMM ist zu AC rechtwinklig.
5. zusätzliche Erklärung.
116. Wenn b größer oder kleiner angenommen wird, wird die Kurve CMM auch eine andere sein, und auf diese Weise entstehen unbegrenzte Kurven, die vom Kreisbogen in gleiche Zeitabschnitte geschnitten werden. Und diese Kurven werden alle untereinander ähnlich sein, wegen des Parameters b, welche in der Gleichung mit x und y die Gleichförmigkeit darstellt. Aus einer gegebenen Kurve AMM können unzählige andere konstruiert werden, die Abszissen und die zugefügten Kurven CMM werden selbstverständlich in dem Verhältnis vergrößert und verkleinert, in dem AC oder b vergrößert oder verringert wird.
3. Beispiel
117. Es seien die Kurven AM, AM alle Zykloiden, die in A Spitzen haben und die Vertikale AC in A berühren. Gegeben den Parameter jeder der Zykloiden AM oder den Durchmesser das Doppelte des erzeugenden Kreises = a; aus der Eigenschaft der Zykloide oder und daher . In diesem Fall ist , die Funktion von a und x keiner Dimension, wie gefordert wird. Deshalb wird für die Kurve CMM jene Formel oder gefunden. Wenn die Gleichung in den Koordinaten x und y gewünscht wird, aus der Gleichung oder deren Differenzial wird auch a variabel gesetzt, der Wert von a muss eingesetzt werden. Aber diese differenzierte Gleichung auch mit a variabel gesetzt gibt oder . Die übergeht in diese . Aber die obere Formel multipliziert mit ergibt diese . Diese beiden Gleichungen addiert ergeben eine integrierbare Gleichung, deren Integral ist . Aus der der Wert von a herausgezogen wird ergibt und . Mit welchen Werten in der Gleichung , die aus zwei Differenzialen unter Streichung von da entsteht, wird hervorgehen für die gesuchte Kurve CMM.
6. zusätzliche Erklärung.
118. Aus dieser Gleichung wird der Berührungswinkel gefunden, den die Kurve CM mit der hinzugefügten PM bildet nämlich . Hierauf wird auch der Berührungswinkel, den die Zykloide AM mit der hinzugefügten PM bildet. Aus der Gleichung der Zykloide wird allerdings sein. Diese Berührung wird aber durch Eliminieren von a sein. Deshalb weil der eine den anderen dieser Winkel der Ergänzungswinkel ist, diesen genommen nacheinander eingesetzt, wird der rechte Winkel sein, den die Kurve CMM mit der beliebigen der gegebenen AM bildet. Folglich ist die Kurve CMM die Senkrechte zur Bewegungslinie aller gegebenen Zykloiden AM, AM, u. s. w.
7. zusätzliche Erklärung.
119. Nimmt man ein AC einer anderen Größe, werden auch andere Kurven CMM hervorgehen, und so werden unbegrenzte rechtwinklige Trajektorien gefunden, die alle untereinander ähnlich sind. Also aus einer gegebenen wird es erlaubt sein, alle beliebigen zu erzeugen.
4. Erläuterung.
120. Alle diese Kurven, die die isochronen Winkel abschneiden, jede beliebige der Kurven werden schneiden, können immer konstruiert werden, auch wenn dies aus der Gleichung nicht so erscheint. Denn durch Quadrieren können aus den gegebenen Kurven die Winkel abgeschnitten werden, die zu gegebener Zeit den Abstieg vollenden werden, und auf diese Weise können die Punkte einer beliebigen gesuchten Kurve gefunden werden. Wenn allerdings die geschnittenen Kurven algebraisch sind, ist die Gleichung für die schneidende Kurve so zusammengestellt, dass durch die ausgeführten erforderlichen Austausche der unbestimmten a gegenseitig getrennt werden können. Aber wenn die geschnittenen Kurven durch eine Differenzialgleichung ausgedrückt werden, lässt die Differenzialgleichung für die schneidende Kurve sehr selten die Trennung der Unbestimmten zu. Der Grund ist, weil bei der besonderen Methode, die ich im Falle dieser Zykloiden benutzt habe, der Parameter a eliminiert werden muss; und diese Ersetzung nicht zur Trennung führt.
5. Erläuterung.
Zunächst ist zu beachten, alle Kurven, die isochrone Bögen abschneiden, deren Zahl für verschiedene Werte von b unendlich ist, sind untereinander ähnlich, wenn die abgeschnittenen Kurven so groß gewesen sind. Dies wird berechnet aus der allgemeinen Gleichung in der weil p eine Funktion der selben a und x keiner Abmessung der Mengen a, b und x die Gleichheit bestimmen. Aber aus der Gleichung der zweiten Kurven, weil in dieser a, x und y überall dieselbe Zahl der Dimension zu bewirken gesetzt werden, wird der Wert von a eine Funktion von x und y der gleichen Dimension sein. Deshalb erhält man an dieser Stelle durch Substitution von a die Gleichung für die schneidende Kurve, in der b, x und y überall die gleiche Dimension der Zahlen darstellen. Wird folglich b variabel gesetzt, entstehen unbegrenzt viele untereinander ähnliche Kurven, im Bezug auf A. Mit einer einzigen gegebenen werden also die übrigen leicht aus der Überlegung der Ähnlichkeit beschrieben.
6. Erläuterung.
122. Dieses Thema über die abzuschneidenden isochronen Bögen wurde schon im vergangenen Jahrhundert in der Acta Eruditorum Lipsiae im Jahre 1697 vom berühmten Johann I Bernoulli abgehandelt, und danach in den Notizen der Akademie in Paris vom berühmten Joseph Saurin, die aber eine andere Vorgehensweise verwendet haben. Aber ich habe ein Verfahren gezeigt, das ich in unseren Notizen für das Jahr 1734 mitgeteilt habe, wie die Fragestellungen auf dieses am bequemsten zu lösen sind. Aber an diesen Stellen habe die berühmten Männer so weit auch die ähnlichen Kurven erwogen, wie ich, ohne Zweifel weil die Lösung für unähnlichen Kurven zu schwierig wäre und oft auch die Kräfte übersteigt. Aber in den zitierten Stellen werden diese synchronen Kurven genannt, weil die durchlaufenen Bögen zugleich durchlaufen werden.
7. Erläuterung.
123. Aus meiner Abhandlung in den Berichten der kaiserlichen Akademie der Wissenschaft in St. Petersburg, Band IX, S. 3 ff, 1764 wird offenkundig, diese synchronen Kurven können auf gleiche Weise gefunden werden, wenn die gegebenen Kurven auch nicht ähnlich gewesen sind, sondern jedoch derartig, dass ds = pdx gesetzt wird, in p die Größen a und x die gegebene Zahl der Dimensionen darstellt; denn dann wird gleichermaßen einfach der Wert des Buchstaben q gefunden. Als ob die Zahl der Dimensionen a und x in p n gewesen wäre, wird die Gleichung 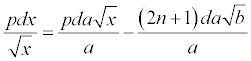für diese schneidende Kurve gefunden werden. Wenn deshalb n = -½, wie wenn 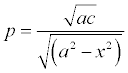gewesen sein wird, wird daher x = ma, oder x im gegebenen Verhältnis zum Parameter a zu verstehen ist: in diesem Fall ist deshalb die Konstruktion der Synchronen sehr einfach. Aber wenn keinen derartigen Wert gehabt hätte, wird aus meiner oben zitierten Abhandlung erkannt, auf welche Weise die gesuchte Gleichung zu suchen wäre.
- Quelle:
- Mechanica sive Motus Scientia Analytice exposita Auctore Leonhardo Eulero. Tomus II. Petropolis 1736
© 2024 Dr. Rainer Stumpe
