Si nullos statuis in coelo solidos orbes, et si omnes planetarum motus administrantur facultatibus naturalibus, quæ sunt ipsis planetarum corporibus insitæ: quæro igitur, quæ futura sit astronomiæ ratio? videtur enim illa circulorum et orbium imaginatione carere non posse?

Fictorum illa circulorum et orbium inutili supellectili carere facile potest, at verarum figurarum, in quas ordinantur itinera planetarum, imaginatione tantum abest, ut privemus astronomiam, ut veri astronomi præcipuum opus et labor sit, demonstrare ex observationibus, quas figuras obtineant orbitæ planetariæ, talesque comminisci hypotheses seu principia physica, ut ex iis figuræ demonstrari possint, consentientes cum deductis ex observationibus. Semel igitur stabilita figura orbitæ planetariæ, in posterum secunda jam et magis popularis erit astronomi exercitatio, calculum astronomicum per hanc genuinam figuram informare et regere, vel etiam illa figura in materialibus instrumentis expressa non secus quam solidis antiquorum orbibus uti planetarumque cursus per has figuras oculis subjicere.

Quam igitur tradis materiam libri quinti, seu theoricæ doctrinæ secundi, et quo discrimine illam separas a præcedentis quarti et sequentis sexti materiis?

Hactenus libro quarto principia physica motuum (inter cetera) sunt demonstrata rationibus et experimentis, quintus ex hisce principiis physicis formabit figuras orbitarum planetariarum earumque figurarum potestates explicabit; ubi erunt excutiendi reconditissimi geometriæ penus. Sextus vero usum harum figurarum in theoriis singulorum planetarum docebit et in opus producet. Quartus igitur theoriam habet, quintus organum, sextus praxin; quartus physicus erat, quintus est geometricus, sextus erit proprie astronomicus.

Duæ: in prima eccentricus cum suo plano connectuntur cum causis physicis; in secunda traduntur definitiones terminorum astronomicorum, qui occurrunt communiter in omnibus planetis circa eccentricum hunc, et explicatur ratio calculi quoad hanc partem.

Qualis igitur formatur figura orbitæ planetariæ ex principiis quarti libri physicis?

Si planetæ corpus non haberet fibras magneticas, ut secundum plagam illarum unam in boream eliceretur, secundum alteram in austrum, secundum unam plagam traheretur versus Solem, secundum reliquam expelleretur: tunc Sol, gyratione corporis sui circa suum axem circumferens speciem sui corporis immateriatam per amplissima mundi spatia, planetam illa apprehensum una circumferret et 1) siquidem ille initio constitisset sub ecliptica, totum ejus iter exactissime in planum eclipticæ ordinaret, 2) eoque in id ipsum punctum, unde factum est initium, semper restitueret, 3) idem esset et corporis Solis et orbitæ planetariæ centrum, 4) ipsa figura orbitæ circulus esset absolutissimus, 5) planeta in æqualibus hujus circuli portionibus omnibus æqualissima celeritate veheretur.

Sed quia posuimus, in cujuslibet planetæ corpore duplices inesse fibras, fit igitur permixtione facultatum corporis planetarii et virtutis motricis Solaris: ut 1) planeta describat orbitam ad eclipticam obliquam; et quia fibræ latitudinis fere quidem in parallelo situ manent toto circuitu, non tamen omnino, quin potius paulatim post multas gyrationes inflectuntur, ideo 2) planum, comprehensum orbita planetæ, proxime quidem est planum perfectum, non tamen omnino; quin potius peracto uno reditu centrum planetarii globi non exacte restituitur ad suum initium, sed novum circulum decurso et absoluto connectit, in modum circulorum dierum naturalium, de quibus libro tertio fol. 291, vel in modum fili, quod vermis sericus fundit, domunculam sibi circumjiciens et struens ex plurimorum circulorum connexorum implexione, qua etiam ratione efficitur, ut longissimi excursus ad latera non omnibus sæculis sub iisdem locis zodiaci fiant. Et quia fibræ libratoriæ planetam faciunt altrinsecus a Sole trahi, e regione vero pelli, ideo planeta 3) describit orbitam circa Solem quidem, at non ut circa suum centrum, hoc, est a Sole eccentricam, efficiturque hac ratione 4) non perfectus circulus, sed a lateribus paulo angustior et compressior, nimirum figuræ ellipticæ. 5) Ob eandem causam et quia species corporis Solaris, motum planetæ concilians, in ampliori circulo tenuior et imbecillior est, planeta neque ejusdem celeritatis esse potest in omnibus orbitæ partibus, sed tardus in longa distantia a Sole, velox in parva. Denique quia etiam fibræ libratoriæ situ suo parallelo plurimarum revolutionum successionibus emoventur, ideo etiam loca sub zodiaco, quibus planetæ fiunt altissimi tardissimique, non semper manent, sed paulatim succedunt in consequentia.

Perplexam descripsisti figuram itineris planetarii, nec aptam, quæ oculis, præsertim in plano, subjiciatur.

Etsi hoc verum est, non novum tamen est in astronomia aut privatum Copernici, nec opus est omnia simul in eodem plano repræsentari, sed possunt perplexiones illæ, ortæ a tardissima translatione metarum latitudinis et altitudinis, eadem dexteritate secerni, qua usi sunt veteres astronomi, minori tamen apparatu.

Commenti sunt pro latitudinibus orbem unum, deferentem nodos, extimum totius theoriæ planetariæ; pro altitudinibus vero orbes duos, inæqualis crassitudinis utrumque, quibus nomen dederunt Deferentium Auges.

Quia magis ad physicas rationes motuum imaginationi subjiciendas comparati fuerunt, quam ad astronomicas. Itaque eorum usurpatione stabilirentur illæ physicæ opiniones falsæ de soliditate orbium, vicissim obscurarentur iis sententiæ veræ de causis libro IV. demonstratis harum inæqualitatum earumque transpositionis tardissimæ.

Quid ergo tu his tribus veterum orbibus substituis ad subjiciendas imaginationi rationes astronomicas?

Sufficit, ut duas lineas rectas ex centro Solis educamus, alteram per sectiones orbitæ planetæ cum ecliptica, reliquam per centrum orbitæ planetæ proprium, utramque utrinque usque sub fixas, et illius motum sub ecliptica in antecedentia signa, hujus sub circulo, qui in sphæra fixarum superstat orbitæ, motum in consequentia doceamus, æquabilissimum utrumque, illum ab æquinoctiali puncto medio, hunc a linea illa intersectionum. Nisi hic excipiendum fuerit aliquid libro VII. ex eo fundamento, quod etiam ecliptica luxatilis est, nec semper per easdem omnino fixas tenditur.

Separatione hac facta, quid remanet imaginationi nostræ de figura itinieris planetæ?

Remanet orbita perfecte elliptica, plano mero regularissimo, ad eclipticæ planum constantibus angulis inclinato, a quo eclipticæ plano hæc orbita secatur linea per centrum corporis Solaris ducta, ut fol. 599. libro IV. præmissum. In hæ orbita planeta vehitur inæquali per partes celeritate, restituitur vero ad sectiones adeoque etiam ad æquinoctialia puncta, quin etiam ad fixas adque lineam per centra æqualissimis temporum periodicorum mensuris, quantum in se.

Nihilne peccat hæc imaginatio in causas et mensuras motuum unius periodi physicas?

Nihil penitus, dummodo memoria teneamus, ea, quæ a reali implexione et connexione plurium orbitarum sunt ablata per dictas duas lineas, physice non per illas ipsas, sed per inclinationem fibrarum realium corporis planetarii præstari.

Quo jure hanc quoque partem facis Copernicanæ astronomiæ, cum tamen is auctor manserit in sententia veterum de perfectis circulis?

Fateor, formam hanc hypothesium non esse Copernicanam. At quia pars ista de eccentrico servit hypothesi universali, quæ motu Telluris annuo et quiete Solis utitur, fit igitur a potiori denominatio. Adde quod ista particula hypotheseos necessariis argumentis physicis ex illa quiete Solis et motu Terræ, dogmatibus Copernicanis, nectitur, itaque bono titulo etiam hæc ad Copernicum referri possunt.

Qua methodo incedendum; ut demonstretur, ex causis physicis, libro IV stabilitis, oriri talem figuram orbitæ tantamque per partes ejus celritatem planetæ?

Incipiendum nobis est ab accessu et recessu planetæ a Sole primumque constituenda est mensura geometrica fortitudinis virium, quæ exseritur in planetam librandum in quolibet situ fibrarum. Secundo expedienda est etiam mensura geometrica compendiosa effectus attractionis vel expulsionis, qui toto aliquo arcu orbitæ per omnia virium incrementa fuit accumulatus. Tertio demonstrandum est, ex tali libratione, inter circumeundum peracta, oriri figuram orbitæ ellipticam. Quarto ostendendum est, planum ellipsis exhibere mensuras temporis et morarum, quas planeta consumit in quolibet arcu figuræ suæ ellipticæ. Quinto docenda est æquipollentia inter planum circuli et planum ellipsis, quoad hanc temporis mensurationem. Ultimo denique demonstrandum erit, circumductione fibrarum latitudinis sic comparata, ut libro IV. positum est, inniti æquabilltatem plani orbitæ. Quibus demonstratis securus redditur curiosus astronomus (popularibus enim non est opus libro nec IV. nec prima hac parte quinti) de hac parte calculi motuum, quam pars altera libri V. expedire et liber VI. applicatione hujus orbitæ ellipticæ ejusque plani ad orbem magnum in usum proferre docebit.

I.
De Incremento Librationis.

Incipe a primo et dic, quibus principiis formetur seu determinetur modus incrementi librationis in omni situ planetæ?

Duæ causæ concurrunt ad formationem hujus incrementi, activa et passiva. Activa est modulus virium libratoriarum, respectu sui ipsarum, quantus is invenitur in una qualibet particularum æqualium orbitæ eccentricæ. Passiva est dispositio corporis planetarii ad Solem alia atque alia, quæ non omnis recipit seu admittit totum illum modulum virium, sed quælibet suam propriam portionem.

Tria ista: primo distantia arcus orbitæ a Sole, secundo quantitas hujus arcus, tertio tempus, quod planeta consumit, dum versatur in illa particula.

Quæ est proportio distantiarum, contraria est proportio tenuitatis speciei Solis, quæ una et eadem et circumfert et librat planetam, nunc attrahens illum nunc repellens, ut lib. IV. dictum fol. 526. Itaque quanto longius distat particula a Sole, tanto imbecillius quovis temporis momento planeta in ea versans libratur. Hoc nomine solo Sol absumeret in diversos interque se æquales arcus eccentrici vires inæquales.

Quia in longum arcum profunditur multum virium, parum in brevem: æqualibus igitur arcubus positis, hoc quidem solo respectu vires debentur æquales.

Quid præstat tempus ad augmentum virium seorsim, et quid omnes tres causæ junctim?

Cum planeta, ut lib. IV. fol. 849. 361. ostensum, quo longius a Sole distat, hoc diutius moretur in æqualibus orbitæ particulis, hoc diutius etiam sentiat vim motricem Solis, quanta est in illius particulæ distantia, et vero jam dictum sit, quo longius a Sole distet una quælibet particularum æqualium orbitæ, hoc imbecillius etiam in illa planetam librari: quare quo imbecillius libratur in uno momento temporis in quavis æqualium orbitæ particularum, tanto diutius etiam et versatur et libratur in illa. Cum ergo compenset virium imbecillitatem prolixitas temporis, quo planeta vires illas in se experitur idque in eadem utrinque proportione, earundem scilicet distantiarum a Sole, hinc tandem efficitur, ut in particulas eccentrici æquales modulus etiam virium libratoriarum exseratur a Sole quidem et respectu ipsius, ut agentis, æqualis penitus. Vide fol. 349. 374 schemata.

Iam igitur dic mensuram portionis, quam de modulo Solarium virium admittit in se planeta in quovis situ suo ad Solem.

Attendendus est angulus, quem Solis radii faciunt cum fibris globi planetarii magneticis. Hujus enim anguli sinus complementi metitur hanc virium portionem admissam. Cum enim causæ librationis effectrices sint Solis radius et fibræ magneticæ corporis planetarii, duæ lineæ physicæ, mensuram quoque fortitudinis librationis ab angulo inter has lineas ejusque sinu peti par est.

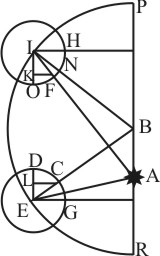Ut si sit A Sol, I, E centrum corporis planetæ, RP linea ducta per A Solem et centrum orbitæ B erunt EG, IH fibræ mageticæ in RP propemodum perpendiculares (saltem compensatione semicirculorum considerata) et H, G termini solipetæ. Positum est enim libro quarto folio 583, fibras in circumlatione corporis manere sibi ipsis propemodum parallelas et in P. R nullam occasionem exhibere tractus vel repulsæ, quia ibi loci utrisque terminis, et solipetis et solifugis, æqualiter ab A Sole distant; in locis vero intermediis, ubi termini solipetis vel solifugis recta in Solem spectant, librationis vigorem esse omnium maximum. AE et AI sunt Solis radii. Ducantur ED et IO lineæ ipsi RP parallelæ et in illas perpendiculares ex F et C punctis, in quibus radii Solis secant circulos globi planetarii medios, sintque CL et FK. Hic anguli radiorum Solis cum fibris sunt AEG, AIH, angulorum complementa CED, FIO, seu arcus CD, FO, et horum sinus LC, FK, qualium IH vel EG est sinus totus 100000. Statuitur igitur, sicut se habent EG, IH ad LC, KF, sic esse totum modulum virium ex Sole in I vel E præsentium, ad portionem, quam admittit planeta in situbus fibrarum EG et IH.

Quare sinum potius mensuram statuis, quam anguli vel arcus complementum ipsum?

Quia fibra quælibet magnetica quamvis in globoso corpore insit, non est tamen circulus, sed recta linea physica, quæ fortissime operatur (vel ad patiendum tractum seu ad vires radii Solis in se admittendas fortissime est disposita), cum recta in Solem dirigitur, vel quod idem est, cum est in planum illuminationis circuli (quo finitor pars globi Soli obversa) perpendicularis: cum vero in illud planum est obliqua, æquipollet perpendiculari a suo termino in illud ductæ, ut breviori. Sic Solis radius, secundum calefactionis opus consideratus, quando recto angulo ferit planitiem, fortissime calefacit, quando vero obliquis, jam calefacit minus in ea mensura, quanto quam obliquus radius minor est ducta ex Sole perpendiculari in idem planum (continuatum).

Pulchrior erit consideratio ista: si perpendas, totum globum ex meris fibris constare, quarum longissimæ sunt, quæ insunt in circulo globi maximo, breviores, quæ in lateralibus, hoc pacto non tantum EG vel IH fibra erit, sed etiam, quos tetigimus sinus LC et KF, signatos a radio Solis AE et AI in terminis suis C, F, ii sunt fibræ laterales. Quanto ergo minores sunt CL, FK quam GE, HI, tanto minus virium ex radio Solari admittit in se unaquælibet fibra totius corporis, ob hanc ipsam obliquitatem radii Solis in se. Ita radius ipse Solis, designando fibram lateralem, designat sinum, qui est mensura portionis suæ virtutis in eas receptæ.

Præterea omnis motus naturalis vel artificialis, in quem vel eadem vel analoga concurrunt principia, dispensatur per sinus angulorum: præcipue vero et evidentissime motus vel nisus brachiorum in libra et statera. Cum igitur etiam hæc libratio sit inter motus naturales latiori significatu (quippe potentia librans speciei Solaris est dimensionum particeps et quodammodo, sine tamen materia, corporalis; dispositio vero fibrarum in planeta rursus est corporalis), non est absurdum, etiam hanc librationem accipere leges easdem cum libra et statera. Id tanto magis verisimile de libratione versus Solem, quod ipsa etiam promotio planetæ in longum suæ orbitæ, causa intensionis et remissionis, velocitatis scilicet et tarditatis, ejusdem libræ vel stateræ leges imitator, ut libro IV. dictum folio 533. et 500. infraque pluribus fiet evidens.

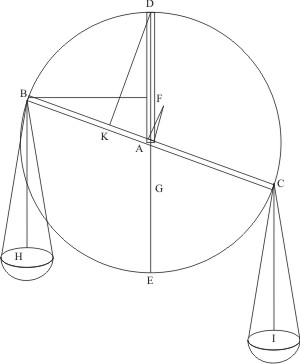Linea ex Sole in fibras habet se instar manubrii in libra, fibræ instar brachii libræ, plagæ fibrarum instar lancium; et quod sunt in lancibus pondera, hoc sunt in planeta attractus ad Solem vel repulsio ab eodem, et utrumque quidem ex eodem rerum genere. Nam ut Sol trahit planetam, sic Terra trahit corpora, ob quem tractum corpora dicuntur gravia. Sol quidem planetam trahit ex una plaga, pellit ex altera, et hoc secundum magis et minus, Terra vero sine discrimine situs trahit pondera. Quod igitur est in libra ponderum inæqualitas, id est in planeta situs fibrarum ad Solem diversitas, ubi planeta idem repræsentat utrumque libræ pondus. Et quemadmodum in libra pondus gravius descendit ad Terram, levius ab ea discedit ascendens, sic in hoc negotio totus planetæ globus sequitur affectionem plagæ præpollentis. Ut si plaga familiaris plus trahitur a Sole, planeta totus accedit a Solem; sin plaga inimica plus pellitur, totus planetæ globus a Sole expellitur. Igitur etiam mensura, qua pugnant inter se pondera libræ, dominabitur in hujus attractionis et expulsionis dispensatione. Jam vero in libra ponderum victoria æstimatur sinu complementi anguli, qui est inter manubrium et brachium ponderis levioris, ut probabitur: quare etiam in libratione corporis planetæ versus Solem passio plagæ de fibra, Soli propioris, vincet passionem plagæ adversæ in proportione sinus complementi anguli, qui est inter radium Solis et fibram. Victoriæ vero effectus, in motu quidem planetarum, est fortitudo librationis cuique loco competens. Hæc igitur fortitudo, seu natum ex illa librationis incrementum, æstimabitur similiter sinu complementi anguli ad fibras.

Sit AD manubrium seu jugum, eique æqualia AB, AC brachia in eadem recta BC, H sit pondus levius, dependens a B, I pondus gravius. a C dependens. Quanta igitur est longitudo brachiorum BC, tantam habent altitudinem pondera (quæ potestate sunt in B, C punctis), de qua inter se contendant: sit ea DE. Nam si pondus majus totum assem vinceret, brachium BA jungeretur manubrio DA, et majus pondus C esset in loco altitudinis E elevaretque minus ad usque summum fastigium D; sed quia non totum assem vincit, ducta igitur a fine brachii B in manubrium DA perpendicularis BF ostendit, quod pondus B tollatur per partem altitudinis FA et tantum etiam C pondus deprimitur, scilicet per AG. Ut igitur est DF ad FE, sic est pondus H ad pondus I, et ut FE ad FG, sic pondus I ad excessum suum super H; et ut DE ad FG vel DA ad FA, sic summa ponderum ad excessum. At si BA statuitur esse sinus totus, FA erit sinus anguli FBA, qui est complementum anguli FAB.

Eodem modo si EA sit radius Solis, BC fibra magnetica corporis planetarii, H vel B vigor expulsionis minor, I vel C vigor attractionis major, quippe C Soli propius accipiatur quam B, tunc si BA refert attractionem valentissimam, angulo BAD nullo, AF repræsentabit tractionem, angulo BAF vel GAC existente.

Stateræ ratio est eadem, hac solummodo diversitate, quod in libra quidem jugum A est medium inter extremitates brachiorum B, C, ac proinde pondera inæqualia effecerunt, ut BC non maneret parallela horizonti: in statera vero ponderum linea manet horizonti parallela, sed jugum dividit longitudinem brachiorum non in medio, sed propius graviori ponderi, sic ut brachia permutatam habeant proportionem ponderum.

Ut si manubrium libræ DA sit æquale brachiis BA, AC, statera sic formabitur, pondera ista, ex B, C dependentia, suspensura ad æquilibrium horizontis. Ex D perpendicularis in BC ducta, quæ sit DK, erit manubrium, et brachia BK, KC; et ut DF prius ad FE, sic hic BK ad KC. Tunc ut BK minus brachium ad KC majus, sic pondus H minos ex C suspendendum ad pondus I majus ex B suspendendum.

Monendus est lector, difficilem esse experimentationem mechanicam, quia mechanice caveri non potest pondus et crassitudo ipsorum brachiorom: debebant autem geometrice constituere meram lineam sine pondere et latitudine. Cui impedimento quomodo ex parte occurrendum, videatur in Archimede.

Teneo mensuram fortitudinis seu incrementi librationis in quolibet situ fibrarum corporis planetæ, petendam a complemento anguli fibræ cum radio Solis; quia vero difficulter patescere videtur hic angulus, eo quod non tantum corpus continue transfertur de loco in locum, sed etiam ejus fibræ inclinantur, mensura hæc incerta eoque inepta videtur ad usum.

Imo propter hanc ipsam inclinationem fibrarum angulus iste in arcum orbitæ potest converti, ut ex hoc arcu prodeat idem sinus, eadem scilicet mensura, qua ratione ad usum illa fit accommodatissima.

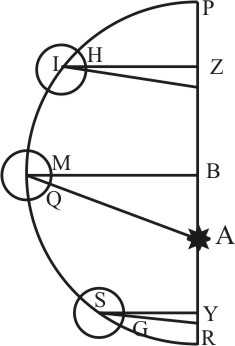Memineris initio, cum planeta est, in apsidibus, hoc est in principio orbitæ, angulum inter radium Solis et fibram esse rectum. Rursum libro IV. fol 593: ostensum est, fibram NQ illius figuræ in ipsum Solem A dirigi, seu cum radio Solis NA uniri, consumto hoc angulo, cum est peractus quadrans orbitæ PN ab apside P, ut ita arcus orbitæ ab apside metiatur complementum hujus anguli. Restat igitur hoc demonstrandum, etiam angulos intermedios fibræ cum Sole, ut HIA, inter rectum et nullum, a mediis arcubus orbitæ, ut PI, inter nullum et quadrantem, sic compleri, ut juncti faciant 90.

Demonstraturque sic: fol. 596. est dictum, sicut est IS ad NB, sic esse sinum anguli HIS ad sinum anguli QNB fere. Id captus causa sic usurpatum fuit de IS et NB, quamvis vi speculationis physicæ verum sit potius de sinibus angulorum IAP, NAP. Jam vero etiam sinus AIB est ad sinum ANB anguli, sicut sinus anguli IAP ad sinum anguli NAP. (Ut enim BI ad BA, sic sinus BAI ad sinum BIA, et ut eadem BI vel BN ad BA, sic sinus BAN ad sinum BNA; ut igitur sinus BAI vel IAP ad sinum BAN vel NAP, sic sinus AIB ad sinum ANB.) Ergo comparatis inter se membris præmissis, invenietur HIS æqualis angulo AIB, et QNB angulo ANB, detractisque æqualibus, erit SIB æqualis angulo HIA (sicut analogice BNB angulo ANA). Sed ipsius SIB mensura est IN, quia ipsius SBI mensura est PI, ergo etiam ipsius HIA mensura erit IN, complementum arcus PI. Dato igitur arcu orbitæ PI, statim datur et SI sinus illius arcus, mensura scilicet incrementi librationis

II.
De Summe Librationis peractæ.

Teneo mensuram incrementi vel vigoris librationis ad quodvis momentum: velim vero scire mensuram partis de libratione peracta principio usque ad illud momentum.

Ea habetur ex ejusdem arcus de orbita confecti sinu verso. Nam sicut se habet tota longior diameter ellipsis ad librationem totam, seu quod eodem redit, semidiameter orbitæ ad eccentricitatem, sic etiam se habet sinus versus ejusque arcus, de orbita ab apside incipientis, ad partem librationis, quæ interim conficitur, dum planeta percurrit arcum illum.

Mediante illa ipsa mensura incrementorum librationis, jam modo sua demonstratione munita.

Sit enim circulus perfectus PD, cujus centrum B, sitque A Sol, linea apsidum PBAR, et P, R summa et ima apsis, et AB eccentricitas, ejusque duplum PB sit libratio tota. Dividatur jam circulus in partes æquales minimas, initio a P facto, sintque PK, KG, GD, DN, NS, SR, et a divisionibus hisce ducantur ipsi PR perpendiculares KX, GF, DB, NA, SY.

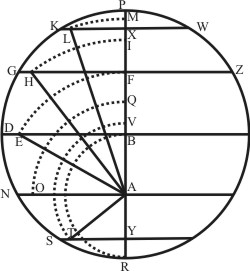Igitur per præmissa, ut sinus KX ad GF, DB, NA, SY, RR (punctum vice lineæ), sic sunt inter se librationis incrementa, ipsis arcubus PK, KG etc. respondentis, puta PM ad MI, IF, FQ, QV, VB, quod verum est eo respectu, quo respectu intelligitur fieri divisio in infinita, quando KX et RR æquales intelliguntur esse. Cum igitur puncta P, M, I, F, Q, V, B ponantur discriminare dicta librationis incrementa: transponantur ea in suas quæque distantias planetæ a Sole A. Centro scilicet A, intervallis AM, AI, AF, AQ, AV scribantur arcus ML, IH, FE, QO, VT, ut sic orbita planetæ elliptica descendere intelligatur ex P per L, H, E, O, T in R, erunt distantiæ planetæ a Sole AP, AL, AH, AE, AO, AT, AR, arcuum vero dictorum PK, PG etc. sinus versi erunt PX, PF, PB, PA, PY, PR. Dico totam diametrum PR, ut sagittam arcus PDR, se habere ad totam librationem PB, sicut sagittæ singulorum arcuum se habent ad incrementa librationis singula, scilicet PX ad PM, sic PF ad PI, sic PB ad PF, sic PA ad PQ, sic PY ad PV.

Nam positum est, librationis partes PM, PI etc. esse in proportione sinuum KX, GF etc. Jam vero etiam totius sagittæ PR partes PX, PF etc. sunt in eadem proportione sinuum KX, GF etc. et cum eadem conditione divisionis infinitæ: ubi (non minus quam prius) punctum R sustinet vicem lineæ RR.

Ergo permutatim partes librationis in eadem proportione respondent partibus sagittæ, et per consequens quælibet portio librationis tota a principio P respondet sagittæ suæ toti in eadem proportione.

Unde scimus, partes PX, XF diametri PR, ut sagittæ consideratæ, esse in proportione sinuum KX, GF, qui eas determinant?

Demonstravit Pappus, Mathematicarum collectionum libro V. prop. 36: si sphæricum, quod intelligatur sub PGZ, planis parallelis quotcunque, ut KW, GZ etc. secetur, superficiem sphærici et axem sectionum, ut PR, secari in proportionem semper eadem: ut sicut est superficies sphærica KPW ad proportionem axis PX, sic etiam sit superficies KWZG ad portionem XF, et sic de cæteris.

Atqui si sphærica superficies intelligatur divisa in zonas infinitas æquelatas, erit quælibet zona, puta KW vel GZ, ut circulus aliquis latitudine carens. Sed circuli KXW, GFZ sunt inter se, causa longitudinis, ut eorum semidiametri KX, GF etc. quare etiam portiones axis PR respondentes, puta PX, XF, tuebuntur proportionem sinuum KX, GF, quibus determinantur.

Demonstrationem ejusdem theorematis per numeros et anatomiam circuli vide tentatam in Comment. Martis, capite LVII. Ibi loci videbatur hæc proportio nonnihil deficere, quia Pappum nondum legeram. Sed causa fuit, quia primam sagittam sumsi arcus non satis parvi, quod perinde est, ac si in Pappo divideres superficiem sphæricam in partes non minutiores, quam unius gradus latitudine. Tunc enim minimæ zonæ latitudo necessario prodiret dupla ejus, quod verum esset.

Etsi arcus circuli PK, KG et reliqui sumti sunt æquales, at arcus veræ orbitæ PL, LH etc. æquales esse non videntur, sed versus E majores: nihilne hoc turbat demonstrationis certitudinem?

Nihil. Nam quod arcus versus E sunt majores, id tribuendum est his ipsis librationibus, ut infra apparebit; idem vero sibi ipsi nec causa solitaria nec concurrens causa esse potest, ut omittam, quod turbela, si qua etiam esset admittenda, plane futura esset insensibilis.

III.
De Figura Orbitæ.

Video mensuram librationis inesse in sinibus versis arcuum orbitæ ab apside inceptorum, ex principiis et causis motuum assumtis; superest ut probes, hac librationis forma constitui orbitam ellipticam, de qua dixisti testari observationes?

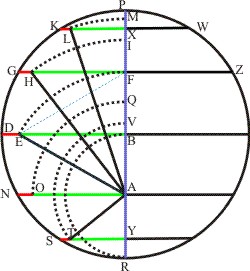Ellipsin fieri orbitam planetæ PLHEOTR et oppositam, demonstratur a proprietatibus identicis hujus figuræ; quas proprietates exprimit libratio hactenus tradita.

1. Constat ex Apollonii Pergæi Conicis, ellipsin, cui circulus est circumscriptus, communi diametro, qui est ellipseos longior, secare ordinatim applicatas ad illam diametrum in eadem omnes proportione segmentorum.

Ut si sint ordinatim applicatæ ad PR lineæ KX, GF, DB, NA, SY, si quidem linea curva PLHEOTR est ellipsis, oportet esse ut DB ad BE, sic GF ad FH et KX ad XL, sic etiam NA ad AO et SY ad YT.

2. Habet ellipsis duo puncta, ex quibus illa veluti centris describitur, quæ focos appellare soleo. Lineæ igitur ex binis focis ad quodcumque punctum ellipsis, aut etiam ex uno foco ad opposita ex centro ellipsis puncta ductæ, semper junctæ sunt æquales diametro longiori: unde fit, ut cum ducuntur ad illa puncta ellipsis, quæ sunt in diametro breviore media inter vertices, quælibet illarum æquet semidiametrum circuli.

Ut si sit A focus, B centrum circuli, AB, BF æquales, erit F focus alter, et AH, HF junctæ erunt æquales diametro PR; sic etiam AL, LF, et AO, OF; quare cum BE sit semidiameter brevior et E punctum in ea, erunt AE, EF æquales et utraque æqualis semidiametro BP, BR vel BD.

Hoc sic applicatur ad planetas, quod observationes testari diximus, planetas tunc distare a Sole (foco altero hujus ellipsis) semidiametro circuli eccentrici, cum quadrantem orbitæ ab apside P præcise confecerunt.

Demonstra, quod repræsententur hæ ellipticæ proprietates in orbita planetæ, quæ ex illis librationibus nascitur.

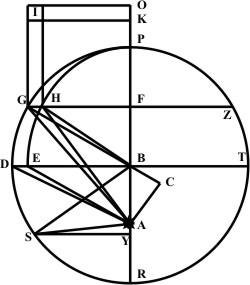Describatur igitur legibus hactenus traditis nova figura, centro scilicet B circulus PDR, quem tangere debeat ellipsis, cujus sit longior diameter PR, et in ea A focus seu locus Solis. Agatur ipsi PR perpendicularis per B, quæ sit DT, erit in ea diameter brevior. Et quia BA eccentricitas est dimidium librationis, tanta igitur competet perfecto quadranti; planeta igitur, in lineam DB incidens, distabit a Sole minus quam in P, differentia BA, distabit igitur quantitate BP, quare intervallum æquale ipsi BP ex A extendatur in DB, sitque terminus ejus E. Planetæ igitur orbita secabit DB in E. Rursum assumatur arcus circuli PG ejusque sinus seu ordinatim applicata GFZ et sinus versus PF. Fac igitur ut BP ad PF, sic BA, dimidiam librationem, ad partem ipsi PG competentem, qua ablata ab AP, residuum ex A in GF extendatur incidatque terminus in H. Dico, ut DB est ad BE, sic etiam esse GF ad FH. Scribantur enim quadrata, super GF quidem GIOF, super HF vero HK, ut sit gnomon HIK; deinde G cum A. et cum B connectatur, et ex A perpendicularis in GB continuatam exeat, quæ sit AC.

Nam quia factum est, ut BP ad PF, sic BA ad differentiam linearum AP, AH, quare etiam ut PB ad BF, sic BA ad excessum, quo AH adhuc superat BP. At etiam ut PB seu GB ad BF, sic AB ad BC, quia GFB et ACB rectangula æquales habent angulos GBF et ABC ad verticem. Ergo BC æquat portionem, qua AH superat BP; at et CG superat BP, hoc est BG, eadem portione BC, quare æquales sunt GC et HA. Sed quadratum rectæ GC una cum quadrato perpendicularis AC juncta æquant quadratum rectæ GA. Ex altera vero parte quadratum ab AF cum quadrato ab FG junctim æquant quadratum ejusdem GA. Ergo æqualia sunt duo quadrata a GF et ab FA juncta junctis quadratis a GC et a CA. Aequalia igitur auferantur, hinc quadratum ab GC, inde quadratum ab æquali linea AH, id est duo quadrata et ab AF et ab FH, scilicet HK: restat hic quadratum ab AC, illic gnomon HIK.

Nam ut unus sinus GF ad suam perpendicularem AC, sic omnes alii ad suas ex A. Ut igitur quadratum sinus GO ad quadratum ab AC, id est ad gnomonem HIK, ita omnium sinuum quadrata ad suos gnomones: quare etiam ablatis gnomonibus, ut unius sinus GF quadratum GO ad quadratum HK ipsius FH, a distantia HA planetæ a Sole determinatæ, ita uniuscujusque sinus quadratum ad minoris a sua distantia determinatæ quadratum. Quorum vero quadrata sunt inter se proportionalia, illa ipsa ut latera sunt proportionalia inter se. Ut igitur GF ad FH, portionem ab AH terminatam, sic quilibet sinus, ut DB ad BE, portionem a sua AE determinatam: quæ ratio est genuina ellipseos.

Ad præscriptum enim legum librationis (quia scilicet in quadrante orbitæ PE consumi debet dimidia libratio ipsi BA æqualis) residuæ BP æqualem ex A in DB extendimus, scilicet AE. Nam quia A focus unus, si ipsi BA statuatur æqualis in BP ex B extensa, designabitur focus alter, cujus ab E distantia erit æqualis ipsi AE, et junctæ æquabunt diametrum: quod fit in ellipsi.

Quæ est proportio DE, latitudinis lunulæ ab ellipsi de circulo resectæ, ad eccentricitatem BA?

Eccentricitas BA est medio loco proportionalis inter DE et ET. Eodem modo etiam omnis perpendicularis, ut AC, est medium proportionale inter GH et HZ residuum subtensæ.

Nam rectangulum sub GH et HZ æquale est gnomoni HIK. Sed hic gnomon est æqualis quadrato AC, ergo et rectangulum GHZ est eidem AC quadrato æquale. Sunt ergo continue proportionales GH, AC, HZ.

Sectis figuris circuli et ellipsis per infinitas GF, DB ordinatim applicatas, primæ portiones in P desinentes (ut GP ad PB) erunt ut GF ad FH, ultimæ in D, E desinentes (ut GD ad HE) erunt inter se æquales, ita proportio DB ad BE, incepta a P, paulatim obliteratur, inque D, E in meram æqualitatis proportionem vanescit. Integri vero arcus a P incepti proportionem inter se habent compositam ex omniam minimarum particularum proportionibus omnibus, eoque nunquam penitus exuunt totam proportionem DB ad BE. Nam quadrantes DP ad PE et sic etiam tota circularis linea ad totam ellipticam est ut DB ad medium arithmeticum inter DB, BE, quod est paulo longius quam medium proportionale.

Quia etiam plani elliptici usus erit, quæro, in qua proportione sit planum ellipsis ad planum circuli, adeoque planum segmenti cujusque de semicirculo ad planum segmenti de semiellipsi, ab eadem ordinatim applicata facti?

Demonstrat Apollonius in Conicis, ubique obtinere proportionem diametri longioris ad breviorem. Ut ei sint ordinatim applicatæ DB, GF: ut est DB ad BE, sic est area semicirculi PDR ad aream semiellilpseos PER, et sicut GF ad FH, hoc est DB ad BE, sic esse et segmentum semicirculi GPF ad segmentum semiellipsis HPF, sic etiam majus semicirculi segmentum GRF ad majus semiellipsis segmentum HRF.

Secetur jam semicirculis per rectam GA, semiellipsis vero per rectam HA: erunt triangula HAF, GAF ejusdem altitudinis FA, quare ut basis GF ad FH basin, sic area GAF ad aream FAH. Atqui ut GF ad FH, sic etiam area GPF ad aream FPH, quare ut GF ad FH vel ut DB ad BE, sic etiam composita area PGA ad compositam PHA.

Velim denique scire etiam proportionem linearum ex centro figuræ in circumferentiam ellipticam ad semidiametrum circuli?

Brevissima quidem, ut BE, minor est semidiametro BD latitudine tota lunulæ DE. At reliquæ omnes, ut BH, minus a BG semidiametro absunt, quam est quovis loco latitudo lunulæ, ut GH.

Trianguli enim GHB duo latera GH, BH juncta oportet superare tertium GB. Major est igitur proportio defectus in E ad defectum in H, quam DE ad GH; hæc vero est sinuum DB ad GF.

Vicissim quadratorum GF et HF proportio est dupla ipsarum GF ad HF. Additis vero BF quadratis ad quadrata GF et HF, summæ quadratorum constituunt proportionem minorem: quare et eorum latera GB, BH minorem constituent proportionem, quam GF, FH. Quo major igitur BF, hoc magis minuitur proportio GB ad BH, ut non æquet GF ad FH. Et vicissim, quo magis crescit PF, hoc magis etiam cresci proportio GB, BH, appropinquans proportioni GF, FH. Sed PF crescit a P tarde, prope DB velociter. Ergo si GH ubique maneret ejusdem quantitatis, tarde variaret defectum HB circa P, velociter circa D. At non manet GH, sed crescit circa P velociter, circa E tarde, scilicet cum ipsis sinibus GF, DB. Rursum igitur defectus HB crescit circa P velociter, circa E tarde. Minor igitur est proportio defectus EB ad defectum HB, quam sagittæ PB ad PF sagittam. Atqui etiam arcus DP ad PG proportio major quidem est, quam sinus DB ad sinum GF, minor vero, quam sagittæ BP ad sagittam FP. Ergo proportio defectus linearum BH appropinquat proportioni graduum PG. Vergit tamen versus D quidem ad proportionem sinuum DB ad GF, at versus P ad proportionem sagittarum BP ad FP.

IV.
De mensura temporis, seu moræ planetæ in quolibet arcu orbitæ.

Qua ratione planum elliptici segmenti fit aptum ad mensurandam planetæ moram in illius segmenti arcu?

Non aliter, quam si divisione circuli in partes æquales constituantur arcus ellipseos inæquales, et parvi circa apsidas, majusculi circa longitudines medias, in hunc modum.

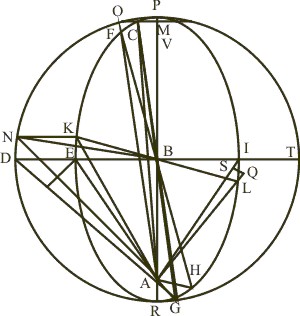Centro B intervallo BP scribatur circulus PDRT, ejus diameter PBR, et in eo, ut in linea apsidum, A Sol, fons motus versus R, AB eccentricitas, eique æqualis BV versus P, ut P, R sint apsides.

Jam punctis A, V focis existentibus, scribatur ellipsis, tangens circulum in P, R, quæ sit PERl, repræsentans orbitam planetæ; et sit diameter brevior EI, circuli vero DT, erecta ad PR ad angulos rectos.

Dividatur jam semicirculus PDR in partes æquales minutas, et sint P, O, N, D, R. T signa inter divisiones, ex quibus ducantur ipsi lineæ apsidum PR perpendiculares, ut OM, NK, secantes ellipsin in C, K punctis. Connexis igitur punctis C, K, E, I sectionum eum A Sole, dico moram planetæ in arcu PC mensurari ab area PCA; sic moræ in arcu PCK mensuram esse penes aream PCKA, et moræ in PE mensuram penes aream PEA, denique moræ in PER, semisse orbitæ ab apside P ad apsidem R mensuram esse aream PERP quæ itidem semissis est areæ totius ellipsis PERIP.

Ostende, quanam in proportione per hanc sectionem orbitæ planetæ partes mediæ fiant majora partibus circa apsides.

Sint enim in circulo partes æquales PO et ND, illa apud apsidem P, hæc apud longitudinem mediam D. Cum igitur iis respondeant de secta ellipsi arcus PC, KE, jam supra dictum est, KE esse æqualem ipsi ND (supposita divisione minutissima), erit igitur KE etiam æqualis ipsi PO. Amplius dictum est, sicut se habeat OM ad MC, hoc est DB ad BE, seu semidiameter longior PB ad breviorem BE, sic se habere PO arcum circuli ad PC arcum ellipsis: ut igitur PB ad BE, sic etiam erit KE arcus ellipsis in media longitudine ad PC arcum in apside.

Hoc sequitur, ut arcubus orbitæ circa ambas apsidas simul sumtis, minoribus existentibus, et arcubus circa utramque longitudinem mediam simul sumtis, majoribus existentibus, attribuantur pro mensuris morarum in iis areæ æquales: cum tamen illi simul sumti distent æqualiter a Sole cum his simul scriptis.

Sint enim æquales ut supra PC et RG, erunt etiam æquales areæ PCB et RGB. Sint iterum æquales KE et LI inter se, majores vero prioribus, ut jam demonstratum est: erunt etiam æquales areæ KEB et LIB.

Jam vero demonstratum est, ut se habet PB ad BE, sic se habere (in tradita sectione orbitæ) KE ad PC. Sunt igitur triangula BPC et BEK (rectilinea vel quasi) αντπιποκδοτα, quia ut altitudo unius BP ad altitudinem alterius BE, sic basis hujus KE ad basin illius PC. Quare areæ BEK et BPC sunt inter se æquales. Igitur et junctorum BEK, BIL areæ sunt æquales areis junctorum BPC, BRG. Sed BPC, BRG junctæ sunt æquales junctis APC, ARG, quia altitudines BP, BR æquales sunt junctæ altitudinibus junctis AP, AR, Et BEK, BIL junctæ areæ sunt æquales junctis AEK, AIL;quia super basibus EK, IL, seu earum contingentibus in E, I, triangula BEK, AEK, item BIL, AIL habent easdem altitudines BE, BI et bases easdem, illa EK, hæc IL. Igitur hic areæ EAK, IAL tribuuntur longis arcubus KE, LI, iisque æquales areæ APC, ARG tribuuntur brevioribus arcubus PC, RG junctis, cum tamen illorum distantiæ a Sole EA, AI junctæ sint æquales junctis horum PA, AR, ut prius est demonstratum.

Si inæqualibus æqualiter a Sole distantibus assignantur æquales areæ, tempora vero 8eu moræ inæqualium, æqualiter a Sole distantium, etiam inæqualia esse debent, per axioma superius usurpatum: quomodo igitur areæ æquales moras inæquales?

Etsi hoc pacto bigæ arcuum sunt inter se re vera inæquales, æquipollent tamen æqualibus in participando tempore periodico.

Dictum quidem est in superioribus, divisa orbita in particulas minutissimas æquales, accrescere iis moras planetæ per eas in proportione intervallorum inter eas et Solem. Id vero intelligendum est non de omnimoda portionum æqualitate, sed de iis potissimum, quæ recta objiciuntur Soli, ut de PC, RG, ubi recti sunt anguli APC, ARG; in ceteris vero oblique objectis Intelligendum est hoc de eo solum, quod de qualibet illarum portionum competit motui circa Solem. Nam quia orbita planetæ est eccentrica, miscentur igitur ad eam efformandam duo motus elementa, ut hactenus fuit demonstratum, alterum est circumlationis circa Solem virtute Solis una, reliquum librationis versus Solem virtute Solis alia, distincta a priori. Ut in IL termini I et L inæquales habent distantias ab A fonte motos, continuata igitur AL in Q, ut AQ sit quantitate media inter AL et AI, et centro A, intervallo AQ scripto arcu QS, secante longiorem AI in S, arcus quidem QS est de priore motus compositi elemento, differentia vero inter AL, AI seu LQ et SI junctæ portiones sunt de posteriore motus elemento, quod jam mente separandum est: nihil enim ei debetur de tempore periodico, cum jam in superioribus suam portionem acceperit, ubi de libratione agebatur, legibus aliis. Atqui non alia via separari potest hoc alterum motus elementum, quam sectione illa orbitæ in partes inæquales, quam supra tradidimus. Quantum enim excedunt junctæ KE, LI junctas PC, RG, totum id est de posteriori motus elemento, et illo excessu separato, relinquitur de priori elemento aliquid, quod est æquale junctis PC, RG, quod sic demonstro.

Quia enim AE, AI per superius demonstrata sunt æquales ipsis BP, BR, quare scriptis arcubus per E, I signa, quorum ille de area AEK tantundem absecat et excludit versus K, quantum iste ad AIL adsciscit supra L, ut ita triangula (sectores verius) novas has bases rectas nanciscantur loco basium obliquarum KE, LI, fiet ut area, junctis PCB, RGB æquali, ad AE, AI applicata, bases etiam seu arcus per E, I scripti fiant æquales basibus per P, R scriptis. Atqui prius est demonstratum, junctas areas KEA, LIA esse æquales junctis PCB, RGB. Quod igitur de obliquis basibus KE, LI pertinet ad circumlationem circa Solem, id æquale est arcubus PC, RG junctis, ubi nulla fere miscetur ei libratio versus Solem, quia AP, AC sunt in differentia insensibili, sic et AR, AG.

Eadem demonstrabuntur etiam de aliis particulis orbitæ: ut si sumatur CF et continuatis CB, FB in G et H, adjungatur respondens ei GH punctaque quatuor cum A fonte motus connectantur. Nam demonstratum est in superioribus, junctas CA, AG, nec non et junctas FA, AH æquales esse junctis PA, AR seu PR diametro longiori; quare etiam ut prius, areæ ACF, AGH junctæ erunt æquales junctis BCF, BGH et per has junctis APC, ARG, quamvis CF per institutam sectionis rationem evaserit paulo longior quam PC et GH longior quam RG. Arcus enim novi, centro A, intervallis AC, AG scripti et secantes ipsas AF, AH, juncti æquabunt arcus PC, RG, quia quanto ille majoris circuli arcus est quam iste, tanto minorem ille angulum CAF metitur, tanto hic majorem GAH, ut sic semper juncti anguli CAF, GAH maneant æquales junctis PAC, RAG.

Cum igitur æqualitas alterius elementi in motu planetæ, scilicet promotionis circa Solem, consistat in æqualitate angulorum circa Solem, binorum puta junctorum invicem, sit vero inter arcus, qui subtendunt hos angulos, distributa ellipseos area æqualiter, binæ scilicet areæ binis aliis semper sint æquales: recte igitur (hactenus quidem et in quantum de bigis arcuum agimus) area pro mensura temporis constituitur; quippe etiam moræ temporis æqualibus, non omnimodis arcubus, sed eorum promotionibus circa Solem, in eadem a Sole distantia, debentur æquales.

Sit igitur hoc pacto recte distributa area ellipseos inter bigas oppositorum arcuum: demonstra nunc, singula triangula seorsim singularum morarum esse mensura justissimas.

Nam quia secundum axioma nostrum mora planetæ in arcu PC est ad moram in arcu æquali RG, sicut distantia illius a fonte motus AP ad distantiam hujus AR, est vero etiam area trianguli PCA ad aream trianguli RGA (quod basin RG habet æqualem basi prioris PC) ut altitudo illius PA ad altitudinem hujus RA: quare mora planetæ in arcu PC est ad moram in æquali arcu RG, sicut area trianguli PCA ad aream trianguli RGA.

Eodem modo demonstrabitur etiam mora planeta in CF, potestate æquali ipsi CP, esse ad moram ejusdem in GH, sicut est area ACF ad aream AGB, ubi summa utriusque areæ æqualis est summæ priorum et sic consequenter. Tota igitur area ellipseos, secta ex A in triangula, eadem proportione distribuitur inter arcus, qua etiam totum periodicum tempus inter eos est distributum. Triangula igitur singula justissimæ sunt in proportione mensuræ singulorum suorum arcuum.

Demonstratio hujus plenariæ æquipollentiæ traditur in Commentariis Martis cap. LIX.fol. 291, cujus folii linea 13.a fine unica vocula erit obscuritatem magnam induxit; quam si mutaveris in computaretur, omnia erunt planiora. Quamquam fateor, obscurius ibi traditam plusque operæ natum ex eo, quod distantiæ ibi non ut triangula consideratæ sunt, sed ut numeri et lineæ.

V.
De Æquipollentia plani circularis et plani elliptici in mensurandis moria arcuum.

Durum et insolens, quin etiam intricatum esse videtur negotium, ut calculator in computatione temporis redigatur ad planitiem figuræ ellipticæ.

Imo usurpatione plani circularis loco elliptici fit omnium opinione facilius, adeo ut vetus calculus huic novo in facilitate nequaquam comparandus sit.

Repetatur igitur figura pag. 662 exhibita, qua generationem plani elliptici demonstravimus.

Et quia hactenus hoc est demonstratum, quod sicut se habet semissis temporis periodici, quo planeta peragrat semissem orbitæ PER, ad tempus, quod planeta consumit in PH vel in PE, sic etiam se habeat ad unguem area PER ad aream PHA vel PEA, supra vero hoc etiam est demonstratum, quod area PDR sit ad PER ut PGA ad PHA et ut PDA ad PEA, omnium enim erat proportio eadem, quæ DB ad BE. eoque etiam permutatim: sicut se habet area PER ad PHA vel PEA, sic etiam se habeat area PDR ad PGA vel PDA, sicut igitur se habet semissis temporis periodici arcus PER ad tempora arcus PH vel PE, sic se habet area PDR ad PGA vel PDA. Quare in his segmentis plani semicircularis inest exactissima mensura morarum, quas planeta nectit in unoquolibet arcui ellipsis.

Assumto segmento PGA, ducatur ex G recta in centrum B. Datur igitur proportio sectoris GBP ad totum circuli planum ex quantitate arcus PG data, ut non sit opus computatione. Totum enim tempus periodicum totumque planum circuli dividitur in 360 partes more astronomico. Restat igitur altera pars segmenti GBA. Atqui hujus computatio facilis est. Ut enim DB sinus totus ad GF sinum arcus PG dati, sic est DBA ad aream GBA. Semel itaque constituta area trianguli DBA maximi, multiplicata scilicet dimidia. eccentricitate in sinum totum et facto in denominationes astronomicas converso, postea semper erit utilis.

Est in theoria Lunæ peculiaris ejus usus ad demonstrandam ejus inæqualitatum unam, quam illa singulariter habet præ ceteris planetis. Sed quia hic liber V. datus est iis tantum proprietatibus, quæ communiter insunt planetis omnibus, igitur, quod restat apparatus geometrici ad absolvendam hujus singularis usus demonstrationem, id differtur recte in libri VI. partem 4, scilicet in ipsam theoriam Lunæ.

Qua ratione vetus Ptolemaica astronomia metitur moras planetæ in quolibet arcu sui eccentrici, seu quid habet illa loco plani circularis?

Utitur ad hoc circulo peculiari, cui æquantis nomen est positum, cujus centrum esset in figuris nostris alter focorum, in proximo schemate V, in antepenultimo F, quia tantum distat a centro eccentrici B versus summam apsidem P, quantum A Sol ab eodem centro eccentrici distat versus imam R. Nam ejecta linea ex centro æquantis V per corpus planetæ, arcus hujus æquantis, interceptus inter hanc lineam et inter VP, lineam apsidum, statuitur mensura temporis, quod planeta consumit in arcu suæ orbitæ.

Videtur hypothesis ista commodior esse ad manuarias ostensiones per instrumenta, theorias dicta: cur istam non retines, cum jam bis adhibueris et ipse vicarias quantitates loco verarum?

1. Quia æquans nunquam perfecte verum dicit, nisi velimus centrum ejus inæquali motu libratile facere, qua ratione recederemus a simplicitate hypothesium multoque perplexiorem et operosiorem constitueremus astronomiam in usu, quam illa est bis duobus libris, quarto et quinto, in causarum explicatione: cum hisce causis semel perceptis, imo etiam non creditis, sed saltem positis, usus postea parte altera libri V. et libro VI. facilis sit.

2. Quia æquantis hujus ratio penes Ptolemæum alia est in planetis superioribus, alia in inferioribus duobus, alia in Luna, essetque nunc etiam alia in Sole; at planum circuli eccentrici penes nos in omnibus planetis eidem usui servit eodem modo.

3. Quia circulus æquans a causis genuinis motuum recedit longissime, quas planum circuli de propinquo repræsentat, quippe quod est cum plano ellipsis sub eodem genere.

Eadem intelligantur dicta etiam contra alias æquipollentias, quas mira vis humani ingenii proferre solet, ut quod David Fabricius unica (quamquam duorum æqualium circulorum contrariis motionibus indigente)libratione centri eccentrici in ellipsis nostræ breviori diametro et salvat ingressus planetæ a lateribus nostri eccentrici circuli immobilis, et simul librat apsida, sic ut jam ipse circulus eccentricus numeratione ab apside libratili usque ad corpus planetæ continuata præstet nobis mensuram temporis. Nec enim mera æquabilitas motuum, nec præcisio omnimoda obtinetur, nec operæ compendium fit, et causæ motuum occultantur abneganturque.

Omnibus vero modis repudiatur Copernicana machinatio, qui duos epicyclos proportione motuum dupla circumfert in concentrico: cum enim observationes testentur, ingredi planetam ad latera locis mediis inter apsidas, hæc Copernicana hypothesis facit ipsum contraria potius ratione evagari extrorsum. Hæc particula hypothesium Copernici emendanda omnino est, salva tamen ejus universali hypothesi motus Telluris annui, unde huic doctrinæ nomen est.

VI.
De regularitate excursuum ad latera.

Num etiam latitudinis calculus certus est, si nulli sunt solidi orbes, et si etiam hoc præstant peculiaria in corpore planetæ filamenta?

Positis, quæ libro IV. fol. 383 s. sunt posita quæque sunt omnino et possibilia et consentanea: necesse est omnino, nasci planum ellipsis perfectum.

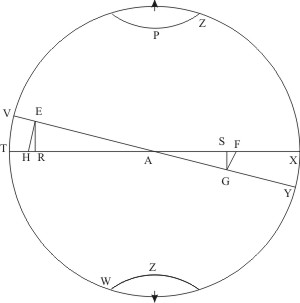Sit enim in præsenti schemate TZX circulus per polos eclipticæ, A vel Sol sit, si TZX est planum, vel si TAX hemisphærium, sit A locus primum inferioris in cavo sectionis eclipticæ TX cum EG orbita planetæ, ut ejus poli sint sub Z, W. Dirigantur fibræ latitudinis secundum GA habeantque facultatem deflectendi motum XVT, a Sole illatum, angulo GAX; et maneant fibræ toto ambitu parallelæ. Manifestum est, planeta in A, sectione inferiore, versante, fibras tensas secundum GA directuras planetam angulo toto et planetam in plano perfecto venturum usque in G, ascendendo usque in planum per polos ductum. Et quia jam fibra ex G in ipsum Solem A dirigitur, non in transversum eclipticæ, ideo neque hic amplius excurret planeta, sed erit G limes; inde paulatim elevatus supra planum ZXW, diriget fibram in lineam ductam ex A sectione per A Solem, donec veniat in A, sectionem jam superiorem convexæ superficiei. Quemadmodum igitur in A maximus est angulus inclinationis fibræ ad eclipticam TX, qui decrescit celeriter, at in G, E nullus est angulus inclinationis fibræ ad eclipticæ longitudinem diuque consistit . hæc inclinationis parvitas: sic etiam si ex circuitu EAG fiat integrum planum, partes ejus apud A inclinatissimæ sunt ad eclipticam TX citoque decrescit inclinatio. At circa G, E plani margo deorsum in sphæræ profundum vel sursum porrigi intellectus, decurrit diu propemodum parallelus eclipticæ plano. Ergo si pro fibræ operatione usurpemus opus ipsum, scilicet EAG, ut planum perfectum, calculus erit principia omnino consentiens.

Conclusio primæ partis de libro V.

Hæc igitur hactenus scripta sunto geometris acri ingenio præditis, qui nihil in calculum recipere dignantur, quod non sit demonstratione accuratissima munitum exque ipsis principiis motuum naturalibus deductum.

Libri V.
Pars Altera.

De terminis Astronomicis & calculo, es orbita eccentrica orientibus.

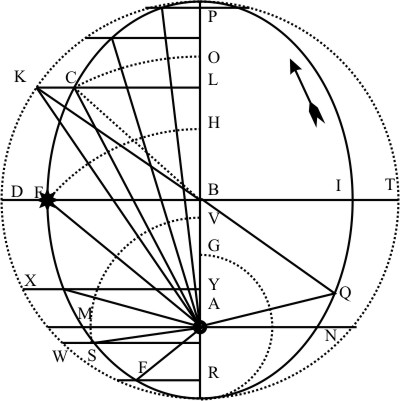Appelatur veteri voce Eccentricus subaudi, Circulus. Et si enim orbitæ sunt Ellipticæ, ut hic PERI quæ habent duo quasi centra A, L quæ physice Focos dicimus, & in eorum altero A Sol ipse ut centrum mundi, inest: tamen etiam punctum inter focus medium, ut B a scriptoribus Conicis centrum figuræ, peculiati iuro dicitur: & præterea ipsi figuræ circulus perfectus PDR metieati causa circumscribitur, centro B diverso a centro mundi A.

Dicitur linea Apsidum, quia cum ducatur per centra A mundi & B orbitæ sectionibus cum orbita monstrat P summam apsidem, & R imam.

Vox Apsis est a rotis ducta, sunt enim puncta Eccentrici, illud P remotissimum ab A Sole, hoc R proximum illi. Sed in Geometria, ratio significationis sit evidentior. Vox enim Apsis a tangendo est nuncupata, & vero in PR punctis circulus mensor tangit Orbitam Ellipticam.

Græcam vocem Apsis Apsides latinæ versiones Arabicorum librorum exprimunt per voces Aux, Auges: quasi Arabes Græcum Psi in Xi convertissent. Affirmavit tamen mihi quidam Arabicæ linguæ cognitionem iactans, voce Augh significati altitudinem.

Libro sexto, puncta ista in planetis primariis Aphelium dicentur & Perihelium, in Luna Apogæum & Perigæum.

Qua necessitas nos cogit, pro circulari itinere planetæ, a veteribus credito: supponere Ellipticum id est, deficiens a circulo, & in eo longiorem diametrum: inque illa ipsa Solem statuere?

Utrumque horum demonstratum est observationibus & demonstratione certissima, in Comm. de motibus stellæ Martis: usurpatumque libro IV fol 453 454 in schematibus, & fol 540 577 etiamque libro hoc quinto parte prima. Nisi ergo supponeremus ista, nunquam repræsentarmus Observationes.

Quibus nominibus inter se distinguantur semisses Eccentrici ab hæc linea constituti?

Alter semissis PER vel PDR descendens vel prior semicirculus dicitur, alter RIP vel RTP ascendens vel posterior.

Græca voce εχχειτριτης, est linea connectens centra A mundi (seu corporis circa quod ordinatur motus) & B Eccentrici: scilicet AP pars linea Apsidum PR.

Quod est nomen lineis ex centro corporis, circa quod motus ordinatur, in Orbitam Eccentricam eductis?

Græce dicuntur αποτηματα. Latine intervalla seu distantiæ, in versionibus Arabicorum, dicuntur longitudines, ut AP, AC, AE, AM, AS, AF, AR, AN, AQ, &c.

Longitudo longior in arabicis, seu distantia aphelia vel apogæa AP, longitudo brevior seu distantia perihelia aut in Luna perigæa, AR, et longitudo media, quæ est medium arithmeticum inter longiorem et breviorem; quarum quæ est in semicirculo descendenti, puta AE, prima longitudo media dicitur, quæ in ascendenti, ut AI, secunda.

Metonymice sumitur pro illis punctis orbitæ, quæ obtinent mediocrem a Sole distantiam, ut E, I, quæ scilicet quadrante seu 90 gradibus ab apsidibus distant ante vel retro.

Quandoque etiam sumitur pro puncto ipsius zodiaci, quod quadrante abest ante vel retro a loco zodiaci, in quem linea apsidum producta incidit.

Ubi notandum et cavendum, quod in hunc gradum zodiaci, qui longitudo media dicitur, non ipsa linea AE ejusdem nominis producta incidat, sed potius BE ex centro, vel ei parallela AM, utpote quæ cum PR apsidum linea rectos angulos formant.

Quod nomen est differentia inter longitudinem, seu distantiam mediam, & quamcunque aliam?

Differentia hæc libratio planetæ dicitur, quia tota libratio, ut in motu lancium libræ, tarda est ab initio, cum planeta distat a Sole longissime, et in fine, cum sit Soli proximus; velox in medio.

In schemate, quia AP est longissima distantia, AR brevissima, transferatur igitur AR in lineam AP extendaturque ex A in G, ut tota libratio in unica linea AP veluti quiescente ob oculos poni possit, quæ erit PG, dupla eccentricitatis BA. Tarda igitur est hæc libratio circa P et G, quando scilicet planeta est vel in P vel in R, velox circa H, quando planeta seu linea AH est in AE vel AI translata.

Dixisti, circulum circumscribi Orbita, metiendi causa, dic quot nominibus ille conducat ad metiendam hanc Orbitam?

1. Circulus hic denominat et discernit arcus orbitæ ellipticæ. Ut PC arcus accipit et nomen et determinationem suam ab arcu PK.

2. Circulus prodit mensuras librationum planetæ et sic format longitudines intervallorum planetæ et Solis. Ut AC vel AO determinatur arcu PK seu ejus complemento KD, quia is docet quantitatem librationis HO addendam ad semidiametrum AH.

3. Circulus exhibet etiam mensuram temporis, quod planeta consumit in quolibet arcu suæ orbitæ ellipticæ. Ut per arcum PK discimus quamdiu planeta movetur in PC arcu.

4. His inventis potest etiam indagari angulus ad Solem, quem arcus orbitæ subtendit. Ut sine arcu PK noto, ignorata AC, nequit inveniri angulus CAP.

I.
De Nominatione.

Quomodo circulus denominat & discernit arcum Ellipseos, & quibus mediis, & quare?

Cum elliptica circumferentia te ipsa geometrice nequeat in partes æquales dividi, partesve constitutæ, a numero denominati: circulus igitur, Ellipsis loco, dividitur in partes æquales, ab Apsidibus initio facto: & a divisionum punctis ducuntur perpendiculares in lineam Apsidum, secantes Ellipsin. Arcus igitur circuli, aphelium inter & unamquamque perpendicularem, nomen dat arcui Elliptico, inter eosdem terminos intercepti, accomodans illi suum numerum graduum & minutorum.

Sit PK gr 50 0 pr KL perpendicularis in PR secans Ellipsin in C. Ergo & arcus Ellipseos PC dicitur esse Graduum 50.0 pr,

Atqui falsum est nomen, cum non sit tantus arcus Ellipseos, neque respectu circuli, neque respectu sua totius orbita Elliptica?

Nihil hoc turbat, nihil est enim, in præsentia quidem, nisi nomen: & nomen quidem non mensuræ apparentis, sed determinationis & resectionis Geometricæ: nec opus est sciri genuinam longitudine, ipsius arcus Elliptici, veluti ad mensam ad decempedam: dummodo postea sciamus, hic ipse arcus Ellipseos sic determinatus, quantum angulum faciat apud centrum Solis, & quamdiu planeta commoretur in eo. Quid? Quod prima huius libri V parte demonstro, arcum Ellipseos, si non longitudine, at saltem potestate, tantum esse.

In circulo, dicuntur sinus arcuum circuli, inceptorum ab Aphelio: in Ellipsi, generis voce dicuntur ordinatim applicatæ, puta ad axem. Ut hic KL est sinus arcus KP. CL est ordinatim applicata.

In specie vero, illa quæ per centrum figuræ ducitur, ut EBI diameter brevior, seu figuræ latus rectum dicitur. Possumus uti Græca voce Diacentros. Quæ denique; per centrum solis traiicitur ut MAN nomine caret, licet sit inter præcipuas. Dicatur novo vocabulo Dihelios.

Dividunt orbitam in partes, superiorem & inferiorem, illa quidem in æquales, sed temporis & apparentiæ inæqualis: hæc in partes quidem inæquales & tempore & longitudine, sed quæ tamen, velut ex sole apparent æquales.

Ut EPI qua constituitur ab EBI est quidem 180 Graduum, sed apparet angulo EAI minore, quam 180 Graduum. At MPN segmentum maius absectum linea MAN & MRN segmentum minus, utrumque apparet æquale quantitate 180 Graduum.

II.
De Libratione.

Sit PK arcus Eccentrici minor quadrante verbi causa Gr. 46 18 pr 51 sec eius ergo complementum KD erit Gr. 43.41 pr. 9 sec eiusque sinus BL 69070 & sit Eccentricitas AB; seu dimidia libratio PH 9265 qualium BP est 100000. Multiplicatur igitur 69070 in 9265 & absectis 5 ultimis prodit libratio OH 6399 addenda ad BP vel AH in superiori semicirculo EPI eritque AO vel ei æqualia AC distantia scilicet planeta a Sole 106399 competens arcui PK vel PC qualium quidem semidiameter est 100000.

Si arcus Eccentri fuerit Gr 313 41 pr 9 sec excessus super tres Quadrantes seu 270 Gr erit etiam Gr 43 41 pr 9 sec dans sinum eundem multiplicandum: quo cum extruitur libratio 6399 ut idem addenda quippe in superiori semicirculo, sed ascendenti.

Quodsi semidiameter BP acceperit aliam dimensionem, verbi causa 152342, multiplicabimus et hanc in AC 106399 absectis 5 ultimis, et prodibit AC in hac dimensione 162090.

Artificio Neperiano conficitur tota hæc operatio expeditissime per unicam additionem. Nam sinus arcus KD logarithmus additur logarithmus Eccentricitatis 9265 & Dimensionis proposita 152343 summa quæsita ut Logarithmus, exhibet librationem 9748 addendam ad Dimensionem 152342.

Sic deinde arcus PW maior quadrante, scilicet Graduum 133 39 pr 7 sec Excessus super quadrantem DW Gr 43 39 pr sec eiusque vel sinus vel logarithmus cum dictis duobus principiis, prodit librationem 9777 subtrahenda ab 152341 quippe in inferiori Diacentri semicirculo, ut prodeat intervallum respondens AS 142565.

Idem erit, si arcus Eccentrici habuerit gr 226 20 pr 53 sec. Nam complementum eius ad tres quadrantes erit Grad 43 30 pr 7 sec tantus in ascendenti quantus DW in descendenti semicirculo.

III.
De mora Planetæ in arcu quodlibet.

Et si proprie Anomalia (inæqualitas) est affectio motus Planetæ: astronomi tamen sumunt hanc vocem pro motu ipso, cui inest hæc inæqualitas. Cumque ad motum hæc tria mensurabilia concurrant, spacium traiiciendum, mora temporis in spatio, & apparens magnitude spatii: vox Anomalia omnibus tribus est accomodanda. Et causa quidem temporis, rursum duplex usus est vocis. Nam primo, Ptolemæus ea utitur pro tempore toto, quod planeta consumit interim, dum restituitur omnis eius inæqualitas ad suum principium: totidem numerans Anomalias, quoties hoc fit.

Secundo, partes huius temporis totius, vulgariter Anomaliæ dicuntur. Pro eo, quod Ptolemæus dixit motum Anomaliæ, subintellige, integræ partem confictam.

Tres nuncupantur Anomaliæ in uno quodlibet situ planetæ: 1. Anomalia media. 2. Anomalia Eccentri, & 3. Anomalia coæquata.

Est spacium temporis, quod planeta consumit in quolibet arcus ex orbitæ, ab apside incepto, redactum in partes & minuta, qualium anomalia tota valet Gr. 360 numerationis logisticæ vel Astronomicæ.

Non ab eo, quasi sit quantitate media inter socias, ut paulo post cavebitur sed media dicitur imitatione veteris astronomiæ, quæ Anomaliam mediam nuncupare solet pro motu Anomaliam medio, id est, æquabili: quia tempus sic redactum in denominationem logisticam, indicat cum suo graduum & scrupulorum numero, quantum arcum circuli planeta confecturus fuisset, si toto isto tempore, quod dicimus Anomaliam mediam, incessisset motu æquabili & medio inter tardissimum & velocissimum.

Quomodo definienda vel mensuranda esset Anomalia media in his schematibus, secundum astronomiam veterem?

Constituta linea BL quæ sit ipsi AB Eccentricitati æqualis, in linea Apsidum BP ut prima huius V libri parte dictum: Anomalia media, more veteris astronomiæ esset arcus circuli æquantis ex L descripti in signorum consequentia, comprehensus inter duas lineas ex L alteram per Apsidem P reliquam per corpus planetæ C traductas. Vel esset illarum linearum angulus ad L eiusve complementum ad 4 rectos. Ut hic si C esset planeta, PLC angulus esse posset loco anomalis media fere.

Defini lineam medii motus, & locum medium planetæ, secundum hanc veterem æquantis Hypothesin.

Esset linea ex centro solis in sphæram fixarum educta, parallela lineæ, quæ ex centro Aequantis, seu ex altero foco Ellipsis, per corpus Planetæ ducta est: & harum utravis sub fixis monstraret locum planetæ medium. In schemate si C Planeta, & AM parallela ipsi LC AM esset linea motus eius medii.

Si ergo in hac astronomiæ forma nova nullus exprimitur circulus Aequans, qua igitur in alia quantitate numerabitur, seu mensurabitur Anomalia media?

In area comprehensa inter arcum circuli qui denominat & determinat arcum orbitæ propositum, & inter duas rectas, quæ terminus arcus cum centro solis connectunt. Ut si propositus sit locus planetæ C, ducta ex C ipsi PR perpendiculari, quæ secet circulum PD in K, & connexis P, K cum A area PKA est mensura anomaliæ mediæ, qualium area totius circuli valet gr 360.

Doce computare Anomaliam mediam, seu temporis moram, quam planeta consumit in arcu proposito?

Sit rursum AB Eccentricitas 9265 qualium semidiameter BP est 100000. Ante omnia quærenda est area trianguli maximi, quod habet angulum ab B rectum, altitudinem BD multiplicata hac in ipsius AB dimidium: prodit igitur 463250000 Huius areæ DBA valor est exprimendus numero secundorum scrupulorum, qualium area tota circuli PDT est Partium Grad 360 vel primorum 21600 vel secundorum 1296000. Quia igitur existente BP 100000 area circuli a Geometris proditur 31415926536 fiet area DAB 19110 secundorum.

Detur jam arcus PC per denominatorem suum PK qui sit Gr 46 18 pr. 51. Sinus igitur ipsius PK scilicet KL altitude trianguli BKA multiplicatus in valorem trianguli maximi, reiectis in fine a facto quinque figuris, conficiet valorem trianguli AKB 3819 secunda, qua sunt Gr 3.50 pr 19 sec. Et vero sector KBP valet gradus totidem, quot dati sunt in arcu PK scilicet Grad 46 18 pr 51 sec additis igitur areis fit PKA Gr 50 9 pr 0 sec tanta est Anomalia Media.

Hoc pacto addenda est area Trianguli æquatorii, quamdiu sector vel arcus est minor semicirculo: qui si superset semicirculum, subtrahenda est illa.

Bina quæque triangula, æqualiter remota verticibus, alterun a summe Apside, alterum ab ima magnitudine sunt æquali. Ut sie arcus PK & RW æquales: area BKA, BWA erunt etiam æquales.

Est arcus circuli Eccentrici in consequentia numeratus: interceptusque inter lineam Apsidum & inter perpendicularem illi, per corpus planetæ, sive per punctum quodcunque Orbita propositum eductam. Ut proposito puncto orbitæ C aut planeta in illo versante, si per C ducatur in PAR perpendicularis KCL, secans circulum in K, PK arcus erit Anomalia Eccentri.

Subintelligitur & hic vocula Motus. Nam etsi in arcu ipso circuli PK secundum figuram, nulla apparet inæqualitas vel Anomalia: motus tamen planetæ in Orbita PC vere est Anomalia inæqualis, tribus nominibus, primo ratione suæ figuræ Ellipticæ, quæ secundum diversas sui partes flectitur inæquali curvitate, distatque a centro figuræ inæqualiter: deinde ratione celeritatis quæ non est eadem in omnibus orbitæ particulis: tertio ratione apparentiæ tanquam ex sole, quia partes Orbitæ æquales subtendunt apud solem angulos inæquales. Cum igitur arcus PK ad omnia ista determinanda concurrat, ut prius dictum: quare quo iure verus Astronomia circulum Aequantes introduxit: inque eo numeravit Anomaliam mediam: non deteriori iure nos orbitæ reali PC circumscribimus circulum Eccentricum PK inque eo numeramus Anomaliam Eccentri, usurpantes æquabile aliquid, ad mensurandum id quod est inæquabile.

Et in veteri quidem Astronomia circulus æquans seduxit physicos, ut imaginarentur sibi realem vel circulum vel certe motum: ad hic seduci nemo potest, cum appareat ad oculum, veram planetæ orbitam PC in solis duobus Apsidum punctis P, R cum hoc technico circulo PK concurrere; toto reliquo tractus sese intra illius complexum versus centrum figuræ recipere.

Est arcus circuli magni in latitudine zodiaci per continuationem plani orbitæ planetariæ designati, in consequentia signorum numeratus a loco apsidis usque ad locum ipsum planetæ vel cujuscunque puncti orbitæ apparentem; vel, quod eodem redit, est angulus, quem arcus quilibet veræ orbitæ planetariæ subtendit aut dictæ duæ lineæ formant apud centrum Solis, ejusve anguli complementum ad 4 rectos.

Ut si planeta in C, coæquata anomalia est angulus PAC; et si planeta in Q, tunc anomalia coæquata constat his partibus: PAM, MAR duobus rectis, et insuper angulo RAQ. Quodsi centro A scribatur circulus quantuscunque, et sic etiam circulus sphæra fixarum, circuli hujus arcus, numeratus ab AP in signorum consequentiam usque ad AC vel AQ continuatas, dicetur etiam anomalia coæquata.

Motum anomaliæ coæquatum (vel simpliciter anomaliam coæquatam) dicere consueverunt auctores, non quasi ex proposito motu inæquali fuerit elicitus motus æqualis, sed ratione plane contraria, quod, cum proponatur initio tempus seu portio temporis periodici et cum hoc tempus (redactum in denominationem astronomicam) indicet, quantum arcum circuli planeta, si incessisset motu æquabili, fuerit confecturus intra hoc temporis spatium, jam porro munus sit astronomi ostendere, quantum de motu planetæ vere inæquali apparenti respondeat huic tempori fictoque motui æquabili. Sonat igitur motus coæquatus idem, quod motus æquatione affectus et conversus in apparentem, indutus scilicet illam inæqualitatem, quam ei conciliat apparentia, a qua inæqualitate tota periodus Anomalia dicitur.

Cum igitur Anomalias hasce tres & distinxeris & formaveris per fictitium circulum Eccentricum orbita circumscriptum: quæro an non possit eidem usui esse vera planetæ orbita?

Etsi non est opus, potest tamen per æquipollentiam. Nam ut prima hujus V. libri parte dictum, tempus et sic anomaliam mediam metitur etiam area PCA, et anomaliam eccentri potest, qui vult, intelligere etiam per arcum PC. Angulus vero PAC etiam prius dictus fuit anomalia coæquata.

Numerus graduum et minutorum anomaliæ eccentri semper est medius inter ceteros. Quæ vero media dicitur, ea antequam impleat semicirculum, semper est maxima de tribus, coæquata minima; post semicirculum vero media dicta est quantitate minima, coæquata maxima.

IV.
De Angulo ad Solem.

Varii sunt modi, sed compendiosissimus est, qui utitur intervallo planetæ & solis. Nam illo etiam ad alios usus indigemus.

Sunt autem huius modi casus tres: aut enim est planeta supra Diacentron, aut infra Dihelion, aut inter diacentron & Dihelios.

1. Sit igitur initio planeta supra Diacentron DBT puta in C. & Anomalia Eccentri PK Gr. 47.42.pr.20 sec. & sit per eius complementi KD sinum LB 67.277. investigata planeta libratio 6233 eaque addita ad BF. sit constitutum AC. intervallum planeta & Solis instaque 106233, in dimensione qualium BP. est 100000 in latus igitur LB. sinus complementi apponatur ad BA. eccentricitatem 9265. ut habeatur trianguli CAL. rectanguli latus alterum LA. 76542. Divisa igitur LA appositius 5. Cypheris, per CA. quotiens 72051. ut sinus, ostendit arcum Gr. 46.5 pr. 48 sec. qui est angulus LCA. cuius complementum Gr. 43.54.pr.12.sec est angulus quæsitus LAC. vol PAC.

Si Logarithmum dimidiate divisoris abstuleris a logarithmo dimidiate dividendi, relinquitur logarithmus eiusdem sive sinus, sive arcus.

2. Sit secundo planeta infra Dihelios MAN. puta in S & Anomalia Eccentri PW eiusque excessus supra quadrantem DW. Quem ad modum igitur supra, libratio per BZ sinum illius arcus quasita fuit a radio subtrahenda, ut existeret intervallum iustum AS sit etiam Eccentricitas BA subtrahenda nunc est a BZ sinu, ut relinquatur AZ latus trianguli rectanguli alterum. Rusum igitur diviso numero lateris AZ per 5. cyphrus prolongato, per latus AS prodit sinus anguli ASZ cui æqualis est MAS excessus ipsius quasiti PAS super rectum PAM seu quadrantum.

3. Sit tertio planeta inter DBT & MAN ut si sit anomalis Eccentri PX eiusque excessus supra quadrantum DX sinus BY quo libratio quidem subtractoria computatur, cum sit tensus infra B at cum ipso sit minor Eccentricitate BA ipso iam ab hac auferendus est ut restet YA. Cum hoc igitur & cum intervallo insto agendum, ut in primo casu.

Punctum illud in Zodiaco, in quod incidis recta ex centro solis per corpus planetæ educta.

Est differentia numeri Graduum & minutorum anomaliæ mediæ, a Gradibus & minutis anomaliæ coæquatiæ. Vel, secundum Astronomiæ formam veterem, est angulus in centro solis, eiusque mensura, arcus circuli magni sub fixis, interceptus inter lineas medii & lineas eccentrici motus planetæ. Hic cum sit auferendus in uno semicirculo, addendus in altero ad mediuam, ut fiat coæquata: ex eo composita voce xxxxx est dicta: Æquatio vero inde: quia eius additione vel subtractione ex Anomalia coæquata, quæ inæquales sortitur arcus & tempora in positiones æquales, sit Anomalia media æquabilis.

Duæ sunt partes altera physica, altera Optica dictæ: Illa enim est ob inæqualitatem quæ vere planetario motui accidit ob causas physicas: hæc vero ob inæqualitatem tantum modo apparentem vel quasi apparentem, hoc est, propter maiorem vel minorem remotionem arcus veræ orbitæ a sole. Utraq quodammodo in eodem triangulo discernitur, quod hinc æquatorium dicitur.

Connexis enim terminis eccentricitatis AB tam corpore planeta C pars æquationis physica quidem mensuram invenit in area BAC (vel per æquipollentiam, in area BAK) optica vero pars æquationis æqualis esset angulo BCA si is computaretur: quo semper exiguo minor est angulus BKA cuius esset facilior computatis.

In hac Astronomiæ forma renovata, totius æquationis ex utroque elemento compositæ usus est non necessarius nec valde magnus. Non enim per hanc æquationem, constituuntur Anomaliæ: sed contra per comparationem anomaliæ coæquatæ: (quam prius computamus) cum Anomalia media, elicimus æquationem, si quando ea volumus uti.

In tabulis vero ponuntur tres Anomaliæ distinctæ primo enim Anomalia eccentri ponitur ad sinistram, secundum gradus integros ab 1 ad 180 ordine: idque propterea, quia ab hac data sit initium computandi reliquas, ipsamque etiam Distantiam seu intervallum planetæ & solis: secundo huic anomaliæ Eccentri subiicitur in eadem columnas pars æquationis physica seu valor areæ trianguli æquatorii in gradibus minutis & secundis: ex qua conclusione Anomaliæ Eccentri cum parto æquationis physica in eadem cellulam, intelligimus, additas in vicem constituere Anomaliam mediam respondentem. Tertio adlatus huius in peculiari columnas ponitur Anomalia coæquata, respondens arcui. Si quis iam vult scire æquationem compositam, is Anomaliam coæquata a iuxta posita media, seu a summa Anomaliæ Eccentri & parties æquationis physicæ subtrahat: remanebitque æquatio quæsitæ, quæ in semicirculo quidem descendente habet titulum Subtractoriæ, in ascendente, Adiectoriæ.

Dic tamen quomodo partes ha æquationis inter se mutue comparata, se habeant ad invicem?

Quo minor est Eccentricitas, hoc magnis accedunt ad æqualitatem inter se: in superiori tamen semicirculo, supra diacentron, Paulo minor est pars optica, parte physica, in inferiore infra diacentron, paulo maior.

Ut in adiecto schemate, si A.Sol, PAR linea Apsidum, ei, ad rectos DBT MAN superior semicirculus vel quasi DPT inferior DRT Sint Triangula æquatoria in superiori BCA BFA in inferiori BSA BQA. Cuius igitur area triangulorum sint mensura parties æquationis physica, anguli vero ad CFSQ parties optica: area certe superiors sunt de area totius circuli 360 portiones maiores inferiores vero minores quam earum anguli de quatuor rectis seu 360. Centris enim CS diastematibus CB SB semidiametris, scribantur arcus BL BH terminati in CA & SA continuatam qui arcus metientur angulos C & S æque valent vero iisdem arcubus & area CBL SBH. Sic igitur ha area essent partes æquationum optica, æquales essent ambï varius æquationis partes. At non CBL sed maior area CBA est mensura parties optica, sic non SBH, sed minor area SBA in inferiori Superat igitur pars physica superius, pars optica inferius.

Partium quidem prior, physica, est maxima in DT terminis Diacentri quia nullius trianguli altitude maior esse potest ipsa BD vel BT qui est in circulo semidiametris etiamque in Ellipsi longissima ordinatim applicatorum. Posterior pars optica, si orbita circulus esset, maxima foret in MN terminis Diheliæ: ibi enim perpendiculis ex B centro, ducta in vectorem per A esset longissima, est vero illa sinus anguli BMA parties optica qualium BM est sinus serus. Nam in EA superiorem, iam cadis ex B brevior perpendicularis quam est BA.

Sed quia Orbita planetæ est elliptica maxima igitur pars æquationis opticæ est inter M & D sic inter N & T. Primum enim ipso angulus BMA maior est angulo ADE quia triangulum utrumque est rectangulum, basi eadem & vero DB altitude maior est altitude MA brevior scilicet diameter, quacumque ordinatim applicata. Deinde factis BI signis in medio arcuum DM & TN vel circiter: anguli AEB. AIB sunt iterum maiores ipsi AMB.ANE. Est enim omnium ex centro B in orbitam brevissima BD cæteræ xxxx, hoc longiores, longior igitur BM quam XE sensibiliter: at non sensibiliter longior perpendicularis ex B in AM quam qua ex BE in AE. Maior igitur est proportion MB ad BA quam EB ad perpendicularem suam. Itaque maior etiam angulus BEA quam BMA. Ergo bisecta BA in G ductaque perpendiculari EGI erit maxima optica æquatio circa EI. Sed maxima physica fuit circa DT maxima igitur composite cades medio loco inter DE & TI.

Docuisti computare ex proposita anomalia Eccentri, Anomaliam mediam & Anomaliam coæquatam: at crebrior usus exigis, dat a media, quippe ex dato tempore, invenire reliquas: doce & hoc?

Hic via directa nulla est: sed adhibenda est ei, qui sine tabulis hoc vult computare, regula Positionem: ponendo scilicet Anomaliam Eccentri (in schemate antepenultimo) PK tantam vel tantam, eique sic sumptæ computando suam Anomalia mediam PKA. Nam si ea tanta prodit, quanta proposita fuit, bene erit posita Anomalia Eccentri PK. At si non tanta prodit: ex eo quod prodit, emenda erit position, laborque repetendus.

Posses exemplo docere Methodum commodum, ne inassuetus nimium erret vagis propositionibus.

Resumatur igitur superius exemplum & sit iam dicta anomalia media. Seu area PKA.Gr. 50.9 pr. 10 sec manifestum est, si sciretur area trianguli KBA residuam aream KBP habituram eundem numerum graduum cum arcu suo PK ac proinde ablato valore ipsius KBA a PKA relectum iri Anomalia Eccentri PK Cum igitur PKA maior sit qua PKB erit arcus PX sinus minor: quam sinus GR. 50.9pr.10.dec. minor igitur quam 76775. Sit hic sinus in prima positione 70000 propter facilitate multiplicationis. Ductus igitur hic in valorem DBA trianguli, qui fuit in superiori exemplo 11910 sec abiectus 5 creat BKA 8337 sec seu Gr. 2.18 pr. 57 sec. qua adde ad sinus 70000 arcum Gr. 44.25 fiet area PKA Gr. 46.44 pr. Hac nimio parva est, deficit enim per Gr. 2.25 pr. Cum debuerit prodire Grad 50.9 pr. quanta est data. Maior igitur ponatur sinus in positione secundo addito defectus Grad 3.25 pr. ad arcum prius positum 44.25 ut fiat PC circiter Grad 47.50 pr. cuius sinus est proxime 74000 quem rursus eligo propter facilitate calculi. Hic in 11910 multiplicatus facit BKA iam per 7 pr 56 sec auctius, scilicet Gr. 2.26 53 sec quod adde ad PK secundo positum, scilicet ad PKB Gr. 47.44 6 sec creatur PKA Gr. 50.10 pr 59 sec & abundamus supra debitum Grad 50.9 pr. 10 sec per 1 pr 49 sec. Itaque intelligimus hunc excessum parvulum auferendum a secunda positione ipsius PK fietque Anomalia Eccentri quasita, seu PK gr. 47.42 pr. 17 sec. Id licet comprobare. Est enim sinus huius arcus 71969 qui de 11910 sec vindicat Gr. 2.26 pr 50 secun. pro KBA itaque hoc addito creatur Gr. 50.9 pr 7 sec quod insensibili abest a debito Gr. 50.9 pr 10 sec.

De Deflexione Planetarum ab Ecliptica.

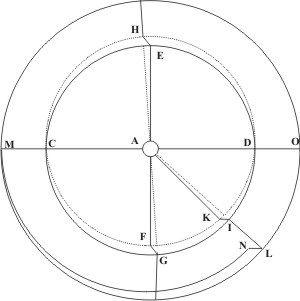
Proprie quidem illa linea, quam planeta vere circa Solem describit centro sui corporis. Ut in schemate si ECGD sit pars plani eclipticæ, HCFD erit orbita.

Secundario vero intelligitur etiam circulus ille maximus, quo planum orbitæ continuatum secat sphæram fixarum. Ut hic MN sectio, facta a plano CAK continuato.

Quid appellas inclinationem planetas vel cujusque puncti in orbita ejus, et. quid circulum inclinationis?

Inclinatio proprie competit non planetis vel punctis, sed lineis vel planis inter se; at quia plana illa circumscribuntur orbitia planetarum et quia in planis lineæ motus planetarum intelliguntur descriptæ, usu receptum est, ut hac voces simpliciter ad planetas ipsos transferantur, causa brevitatis in loquendo.

Cum igitur id, quod infra libro VI. latitudo dicetur, participet etiam de adventitia seu optica inæqualitate, quam secundam indigeramus, quare, ut res diversæ nominibus etiam distinguantur, evagatio planetæ vera ab ecliptica dicatur non latitudo, sed inclinatio; definitur autem sic, quod sit arcus circuli in fixarum sphæra maximi, ex centro Solis descripti 1 ad eclipticam recti, qui circulus inclinationis dicatur, interceptus inter eclipticam et locum planetæ eccentricum. Vel est angulus ad Solem, quem hic arcus metitur.

In schemate si A Sol, FKDHC orbita, MLO ecliptica, puncti K inclinatio erit angulus KAI vel NAL, vel ejus arcus NL ex A Sole descriptus.

Nodi sunt duo puncta eclipticæ, in quibus illa secatur ab orbitæ continuatæ plano. Græce συνδεσμοι, quod iis itinera diversa, Solis apparens et planetæ, connexa sint; ascendens alter, in quo planeta deserto hemisphærio australi deflectit in boream, alter descendens, qui planetam in austrum transponit; vocibus ascendens et descendens ad nostrum hemisphærium accommodatis, ut in quo primi vixerunt inventores astronomiæ. Ut si planum orbitæ et planum eclipticæ concurrant linea CAD, sectionem monstrante, continuata illa sub eclipticam monstrabit M, O nodos.

Limites vero appellantur puncta eclipticæ, quæ quadrantibus a nodis distant; boreus, a quo planeta distat in boream, austrinus, a quo in austrum. Dicuntur limites ex eo, quia planeta, deveniens ad illa puncta, non evagetur ulterius in plagas, sed inde sese convertens incipiat ad eclipticam reverti. Ut in schemate E, G puncta eclipticæ dicuntur limites. Sed et H, F puncta veræ orbitæ, et puncta iis superstantia in sphæra fixarum 1 veniunt eodem nomine et hoc crebrius.

Est arcus orbitæ planetæ sub fixis, interceptus inter nodum ascendentem et locum eccentricum planetæ, numeratus in consequentia. Ut si O nodus ascendens N locus planetæ eccentricus, OMN erit argumentum inclinationis LN. Copernicus pro nodo ascendente sumit limitem boreum.

Secundum principia physica libro IV. usurpata per se quidem immutabilis est, at propter ipsius eclipticæ luxationem, de qua libro VII, per accidens potest mutari.

Non aliter, quam libro III. declinatio puncti eclipticæ, multiplicato sinu inclinationis maximæ in sinum argumenti inclinationis et a facto resectis 5 ultimis, apparet sinus inclinationis. Vide processum fol. 230. et seqq. Si pro sinibus arcuum utaris eorum logarithmis, multiplicatio convertetur in simplicem additionem.

Punctum illud eclipticæ, in quo secatur illa a circulo inclinationis, per locum eccentricum simpliciter dictum traducto. Ut si planeta in K, locus ejus eccentricus (sic simpliciter dictus) sit N et NL circulus inclinationis, angulis NLM, NLO rectis, erit L locus planetæ eccentricus in ecliptica. Non dicitur locus eclipticus simpliciter, quia hic involvit etiam inæqualitatem secundam, libri VI. materiam; sed additur vox eccentricus, ut intelligamus, de illo loco agi, qui determinatur sub ecliptica per solum eccentricum, remoto jam concursu orbis magni, de quo libro VI.

Arcus eclipticæ in consequentia numeratus a principio Arietis usque ad circulum inclinationis planetæ, seu locum eccentricum in ecliptica. Dicitur eccentrica, non quod nomeretur in eccentrico, sed quia eccentricus causatur illam.

Arcus parvus, quo differunt inter se bini arcus, alter orbitæ, alter eclipticæ, a communi nodo incepti et ad circulum inclinationis terminati. Ut hic differentia inter MN et ML.

Non aliter quam libro III. fol. 255. Differentia ascensionis rectæ et arcus eclipticæ respondentis. Multiplicatur sinus complementi inclinationis maximæ in tangentem argumenti inclinationis, et absectis a facto 5. postremis, apparet tangens argumenti reducti.

Vel inclinationis maximæ antilogarithmus additur mesologarithmo argumenti acervaturque hoc modo mesologarithmus arg. reducti.

Compendium utilius, etiam pro ascensione, sit hoc. Maxima reductio circa gradum 45 a nodo ducta in sinum arcus cujusque duplicati, absectis 5 ultimis, constituit reductionem arcui proposito simplo debitam.

Quando planeta pergit a nodis ad limites, auferenda est reductio ab inclinationis argumento, addenda, cum a limitibus ad nodos; quodque hoc pacto conficitur, additum loco nodi ascendentis constituit longitudinem loci planetæ eccentricam.

Est portiuncula distantiæ planetæ a centro Solis, respondens sagittæ inclinationis planetæ, in ea proportione, in qua totum intervallum respondet sinui toto.

Sit A Sol, P, Q poli eclipticæ, TAX repræsentet planum eclipticæ, EAG planum orbitæ; sit planeta jam in E vel G, et centro A intervallis AE, AG scribantur arcus HE, GF, et ex E, G demittantur perpendiculares in TX, quæ sint ER, GS, erunt HR et SF curationes.

Est recta in plano eclipticæ inter centrum Solis et perpendicularem ex centro corporis planetæ. In hoc schemate, planeta in E vel G versante, est AR vel AS distantia curtata.

Distantia proposita, expressa numeris dimensionis cuique planetæ propriæ, multiplicatur in sinum complementi inclinationis distantiæ propositæ competentis, et abjiciuntur a facto 5 postremæ. Seu logarithmus distantiæ additur antilogarithmis inclinationis competentis et fit logarithmus curtatæ distantiæ index.

Circa limites et plus circa illum, qui vicinior est aphelio. Ut si V, Y sint limites, itaque Z, W poli orbitæ, et V vicinior aphelio quam Y, erit HR longior quam FS et longissima omnium.

De Motu Apsidum & Nodorum.

Est arcus orbitæ sub fixis, interceptus inter id ejus punctum, quod eum certo eclipticæ puncto (puta cum principio Arietis vel etiam cum prima stella Arietis) æqualiter a nodo evehente distat, et inter locum summæ apsidis, numeratus in consequentia signorum.

Statuitur æquabilis 1) propter inexspectabilem tarditatem, qua impediuntur astronomi, ut motum hunc per partes singulas exactius considerare non possint, 2) quia habemus exemplum æqualitatis in uno, in quo brevis est apsidis periodus, scilicet in Luna. Itaque principia hujus motus physica, quæ libro IV. fol. 382. delibavimus, ut meris innixa conjecturis, nihil huic æquabilitati præjudicare possunt, quamvis per ea motus iste videatur inæquabilis effici posse. Sed de hoc plura lib. VI. penes planetas singulos.

Quid intelligendum ut per motum Nodorum in primariis, seu quid ut nodi longitudo?

Motus Nodi est arcus eclipticæ, numeratus in antecedentia signorum a certo ejus puncto (puta vel a principio Arietis, vel a loco primæ stellæ Arietis) usque ad locum nodi ascendentis. Quodsi fiat numeratio in consequentia, tunc arcus hic etiam longitudo nodi dici potest.

Etsi rationabile est, etiam hujus puncti, motum in se ipso æquabilem esse, videtur ei tamen inæqualitas inesse nonnulla ex accidenti, propter luxationem eclipticæ, de qua lib. VII.

Nodi quidem sub circuli magno eclipticæ incedunt, limites vero orbitæ, in quantum eorum inclinatio permanere ponitur immutabilis, incedunt in circulis parallelis eclipticæ, vel ei circulo, respectu cujus inclinatio, est immutabilis.

Ad captum juvandum potest eorum motus imaginatione non inepta polorum proponi, dummodo teneamus hoc, physice loquendo polis haud opus esse. Ut in schemate proximo sit orbita VY (continuatione plani transposita sub fixas), ejus poli Z, W moveantur in parvis circellis circa eclipticæ TX polos P, Q. In quam igitur plagam Z vergit a P quovis tempore, in eandem et limes V verget ab eclipticæ parte T et limes Y ab eclipticæ parte X, et ad circuitum ipsius Z in parvo circello, qui sit ipsi TX parallelus, in eandem plagam sequetur etiam limes V in parallelo septentrionali, tanto majori, quanto propior est ipsi TX, et sic Y in parallelo australi. Semper enim erunt in eodem circulo magno inclinationis puncta ista sex: poli orbitæ Z, W, xxli eclipticæ P, Q, et limites orbitæ V, Y.

Hactenus igitur de definitionibus terminorom orbitæ planetariæ eique circumscripti circuli eccentrici, quæ quia communia sunt omnibus planetis, libro hoc V. præmittenda fuerunt. Ceterum usum horom in planetis singulis trademus libro sequenti VI.

Finis Libri V. Theoricæ Doctrinæ II.

Abriss der kopernikanischen Astronomie.
Fünftes Buch.

Zweite theoretischen Lehre.
Über die exzentrischen Kreise, oder die Theorien der Planeten.

Wenn man keine stabilen Kreisbahnen am Himmel feststellt, und wenn alle Bewegungen der Planeten bestimmt werden durch die natürlichen Möglichkeiten, die den Planetenkörpern selbst innewohnen: deshalb frage ich, welches soll die zukünftige Lehre der Astronomie sein? denn man erkennt, dass man nicht auf die Vorstellung der Kreise und Umlaufbahnen verzichten kann?

Auf die Einrichtung jener ungeeigneten Kreise und Umlaufbahnen kann man leicht verzichten, aber es mangelt so sehr an einer Vorstellung der wirklichen Abbilder, in denen die Bahnen der Planeten entstehen, dass wir die Astronomie berauben, dass es die außerordentliche Aufgabe der echten Astronomen ist, aus den Beobachtungen zu zeigen, welche Bilder der Umlaufbahnen der Planeten sie erhalten, und solche Hypothesen oder naturwissenschaftliche Grundlagen zu ersinnen, dass aus deren Bildern die Übereinstimmung und die Ableitung mit den Beobachtungen gezeigt werden kann. Deshalb ist es das einmal begründete Bild der Umlaufbahnen der Planeten, die Übung auch des so sehr beliebten Astronomen im zweiten Schritt, die astronomische Berechnung mit diesem unverfälschten Bild zu unterrichten und zu leiten, oder auch jenes Bild durch sachliche Werkzeuge ausgedrückt nicht anders als durch die festen von den Alten benutzten Umlaufbahnen und den Lauf der Planeten durch diese Bilder vor Augen zu führen.

Epitomes Astronomiæ Copernicanæ

Liber Quintus.Theoricæ Doctrinæ secundus.De Circulis Eccentricis, Seu Theoriis Planetarum.

I.De Incremento Librationis.

II.De Summe Librationis peractæ.

III.De Figura Orbitæ.

IV.De mensura temporis, seu moræ planetæ in quolibet arcu orbitæ.

V.De Æquipollentia plani circularis et plani elliptici in mensurandis moria arcuum.

VI.De regularitate excursuum ad latera.

Conclusio primæ partis de libro V.

Libri V.Pars Altera.

De terminis Astronomicis & calculo, es orbita eccentrica orientibus.

I.De Nominatione.

II.De Libratione.

III.De mora Planetæ in arcu quodlibet.

IV.De Angulo ad Solem.

De Deflexione Planetarum ab Ecliptica.

De Motu Apsidum & Nodorum.

Finis Libri V. Theoricæ Doctrinæ II.

Abriss der kopernikanischen Astronomie.Fünftes Buch.

Zweite theoretischen Lehre.Über die exzentrischen Kreise, oder die Theorien der Planeten.

I.Über den Zuwachs der Libration.

II.Über die Gesamtheit der vollendeten Libration.

III.Über die Form der Umlaufbahn.

IV.Über die Form der Umlaufbahn.

Fünftes Buch.Zweiter Teil.

Über die astronomischen Begriffe und die Berechnung, die aus der exzentrischen Umlaufbahn entstehen.

I.Über die Benennung.

II.Über die Libration.

III.Über das Verweilen des Planeten in einem beliebigen Bogen.

IV.Über den Winkel an der Sonne.

Liber Quintus.
Theoricæ Doctrinæ secundus.
De Circulis Eccentricis, Seu Theoriis Planetarum.

I.
De Incremento Librationis.

II.
De Summe Librationis peractæ.

III.
De Figura Orbitæ.

IV.
De mensura temporis, seu moræ planetæ in quolibet arcu orbitæ.

V.
De Æquipollentia plani circularis et plani elliptici in mensurandis moria arcuum.

VI.
De regularitate excursuum ad latera.

Libri V.
Pars Altera.

I.
De Nominatione.

II.
De Libratione.

III.
De mora Planetæ in arcu quodlibet.

IV.
De Angulo ad Solem.

Abriss der kopernikanischen Astronomie.
Fünftes Buch.

Zweite theoretischen Lehre.
Über die exzentrischen Kreise, oder die Theorien der Planeten.

I.
Über den Zuwachs der Libration.

II.
Über die Gesamtheit der vollendeten Libration.

III.
Über die Form der Umlaufbahn.

IV.
Über die Form der Umlaufbahn.

Fünftes Buch.
Zweiter Teil.

I.
Über die Benennung.

II.
Über die Libration.

III.
Über das Verweilen des Planeten in einem beliebigen Bogen.

IV.
Über den Winkel an der Sonne.