Vektoren werden auf dieser Seite mit fetten Buchstaben in der Frakturschrift bezeichnet. Die Kodierung erfolgt mit Unicode-Glyphen 1D565 bis 1D59F. Diese werden mit aktuellen Versionen vieler Browser dargestellt. Nicht dargestellt werden sie mit Windows^® und iOS^® Versionen von Safari^®.

Der Kreisel

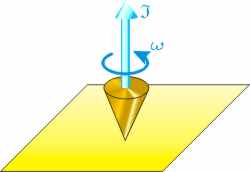Der Kreisel ist ein Kinderspielzeug mit auf­fäl­li­gem Verhalten. Typisch ist er ein Kegel, der, solange er schnell genug rotiert, stabil auf der Spitze steht. Ver­lang­samt sich seine Rotation, so beginnt er zu taumeln und fällt schließlich um (womit er seine stabile Gleich­ge­wichts­lage einnimmt). Was ihn aufrecht hält ist sein Drehimpuls. Denn der bleibt konstant, solange keine äußere Kraft wirkt (1. Newtonsches Axiom), behält also Richtung und Betrag bei. Er beginnt zu taumeln, wenn der Drehimpulsvektor nicht mehr in seiner Sym­me­trie­ach­se liegt (bzw. sein Schwerpunkt über dem Auf­la­ge­punkt). Ursache sind typisch Ungleichmäßigkeiten sei­ner Gewichtsverteilung und / oder Unebenheiten des Untergrundes.

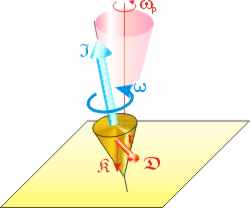Betrachten wir den Zustand des Taumelns, wenn also der Drehimpulsvektor nicht mehr in der Rotationsachse des Krei­sels liegt. Sobald die Rotationsachse des Kreisels geneigt ist, wirkt auf seinen Schwerpunkt die Erdanziehungskraft, die ein Drehmoment 𝕯 erzeugt.

Die Kraft 𝕶 ist die am Schwerpunkt ansetzende Schwer­kraft, 𝖗 der Abstand des Schwerpunktes von der senk­rech­ten Linie über dem Stützpunkt des Kreisels. Die Kraft 𝕶 ist das Produkt aus Masse M und Fallbeschleunigung 𝖌: 𝕶 = M · 𝖌. Der Zahlenwert der Kraft ist also:

• D = M · g · r.

Dieses Drehmoment 𝕯 steht senkrecht auf dem Drehimpuls des Kreisels und verursacht eine zeitliche Änderung der Richtung des Drehimpulses (die Änderung des Drehimpulses ist in Richtung des Dreh­mo­ments!). Als Folge präzidiert der Kreisel, d.h. seine Rotationsachse beschreibt einen Kegel. Die Prä­zi­sions­fre­quenz ω_p ist abhängig vom Drehmoment und dem Drehimpuls des Kreisels:

Die Präzision ist schneller, wenn das Drehmoment größer ist (z.B. wenn die Neigung zunimmt), sie ist lang­sa­mer, wenn der Drehimpuls des Kreisels größer ist. Da der Kreisel durch Reibung Energie verliert (der Drehimpuls nimmt ab) und somit langsamer wird (der Drehimpuls nimmt ab!), nimmt die Prä­zi­sions­ge­schwin­dig­keit zu bis er umkippt.

In Vektorschreibweise ist der Zusammenhang in der Formel beschrieben:

Es gelten für die Richtungen die Regeln des Rechts­systems von Vektorprodukten. (Mittelfinger in Rich­tung Drehimpulsvektor, Daumen in Richtung Drehmoment, dann zeigt der Zeigefinger die Richtung der Präzision an.)

Der Radeffekt

Beim Anfahren unter Motor stellt sich ein unangenehmer Effekt des Drehimpulses ein: das Boot dreht sich um seine Achse! Nicht nur Anfänger haben ihre Schwierigkeiten mit diesem "Radeffekt", wenn sie rück­wärts eine Liegestelle ansteuern.

Was passiert? Wenn der Steuermann Gas gibt, beschleunigen sich die Rotationen des Motors, der Schrau­ben­welle und der Schraube. Da diese Teile, wenn sie rotieren, einen Drehimpuls haben, ändert sich der Drehimpuls des Schiffes. Diese Drehimpulsänderung erzeugt ein Drehmoment, das senkrecht zum Drehimpuls steht. Und dieses Drehmoment dreht das Schiff.

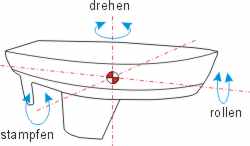Das Schiff hat im Raum drei senkrecht aufeinander ste­hen­de Achsen um die es drehen kann: die Längs­ach­se, die Querachse und die Achse in Richtung Erd­mit­tel­punkt. Die drei Achsen schneiden sich im Drehpunkt des Schiffes (dieser Drehpunkt muss bei einem stabil schwimmenden Schiff oberhalb des Massenzentrums liegen). Die genaue Lage des Drehpunktes ist für ein schwimmendes Schiff schwer theoretisch zu be­rech­nen (Formstabilität!).

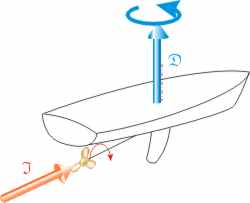Die drehenden Teile einer "rechtsdrehenden Schraube" haben bei Vorwärtsfahrt einen Drehimpuls 𝕴, der in Fahrt­rich­tung gerichtet ist. Wenn beschleunigt wird, ist die Änderung des Drehimpulses in die gleiche Richtung. Das aus dieser Änderung resultierende Drehmoment 𝕯 hat eine Richtung, die aus dem Vektorprodukt der Ab­lei­tung und der rechten Handregel folgt. Man deutet den Zeigefinger zum Zentrum der drehimpulserzeugenden Rotation, den Daumen in Richtung des Drehimpulses, und der Mittelfinger zeigt die Richtung des Dreh­mo­ments. Das Schiff dreht im Gegenuhrzeigersinn (das Heck geht nach rechts). Bei Rückwärtsfahrt ist der Dreh­im­puls vom Bug weg gerichtet, das aus der Be­schleu­ni­gung resultierende Drehmoment ist entgegengesetzt, und das Schiff dreht im Uhrzeigersinn (Heck nach links). Soweit stimmt das mit der Beobachtung und der Merkregel ("als würde die Schraube auf dem Grund laufen") überein.

An der Berechnung bin ich gescheitert. Zwar kann man den Drehimpuls der Schraube (Durchmesser 30 cm, Gewicht 10 kg) bei 600 Umdrehungen pro Minute (10 pro Sekunde) mit einem Ring von 10 cm Durch­mes­ser annähern und erhält einen Drehimpuls von 0,25 N·m, der sich von 0 innerhalb von 10 sec aufbaut. Aber die Effekte der Welle und besonders des Motors sind für mich nicht abzuschätzen. Klar ist jedoch, dass es keines großen Drehmoments bedarf, das Schiff um die senkrechte Achse zu drehen (kann man bei einem ruhig liegenden Schiff durch Drücken am Bug leicht überprüfen).

Bleiben wir beim qualitativen. Da der Motor immer im Gegenuhrzeigersinn dreht (die Drehrichtung der Schraube wird mit einem Getriebe umgekehrt), ist der Radeffekt bei Rückwärtfahrt geringer (die Dreh­im­pul­se des Motors und der Welle/Schraube sind entgegen gerichtet). Versuchen Sie 'mal rückwärts "auf dem Teller" zu drehen.

Die Änderung des Drehimpulses hängt ab von der Zeit in der die Drehzahl geändert wird. Beim sanften Gasgeben dreht das Schiff langsamer, beim Kavalierstart schneller (leicht zu überprüfen).

Der Außenborder hat den Motor (und die Welle) senkrecht eingebaut; damit erzeugt er beim Gasgeben ein Drehmoment, das das Boot um die Längsachse dreht (was sich nur schwach bemerkbar macht). Beim V-Antrieb ist der Motor entgegen der Fahrtrichtung eingebaut: seine Drehimpulsänderung und die der Schrau­be/Welle sind entgegengesetzt und heben einander teilweise auf (der Radeffekt ist geringer).