Metaphy­si­cae cum Geometria iunctae
Usus in Philosophia Naturali,
Cuius
Specimen I.
Continet
Monadologiam
Physicam,
Quam
Consentiente Amplissimo Philosophorum Ordine
Dissertatione Publica
Pro Loco Narenda
Die X. Aprilis Horis VIII - XII.
In Auditorio Phil.
Defendet
M. Immanuel Kant.
Respondente
Luca Divide Vogel,
Reg.Bor. S. Theol. Cultore,
Opponentibus
Ludovico Ernesto Borowski,
Reg.Bor. S. Theol. Cultore,
Georgio Ludovico Meuhlenkampf,
Trempia ad Darkehmiam Borusse, S. Theol. Cultore.
et
Ludovico Ioanne Krusemarck,
Kyrizensi Marchico, S. Theol. Cultore.
Anno MDCCLVI.

Verzeichnis der vorkommenden lateinischen Worte mit grammatikalischer Form und Übersetzung und Erläuterung der zeitgenössischen physikalischen Begriffe.

PRAENOTANDA.

Qui rerum naturalium perscrutationi operam navant, emunctioris naris philosophi in eo quidem unamini con­sen­su coaluerunt, sollicite caveandum esse, ut ne quid temere et conjectandi quadam licentia confictum in scientiam naturalem irrepat, neve quidquam absque experientiae suffragio et sine geometria interprete in ca­sum tentetur. Quo consilio certe nihil philosophiae salutarius atque utilius poterat cogitari. Verum quoniam in linea recta veritatis vix cuiquam liceat mortalium stabili incessu progredi, quin in alterutram partem passim exorbitetur, quidam huic legi usque adeo in­dul­se­runt, ut in indaganda veritate alto se committere minime ausi, semper littus legere satius du­xe­rint et nihil nisi ea, quae experientiae testimonio immediate innotescunt admiserint. Ex hac sane via le­ges naturae exponere profecto possumus, legum originem et causas non possumus. Qui enim phae­no­me­na tantum naturae consectantur, a recondita causarum primarum intelligentia sem­per tantundem absunt, neque magis unquam ad scientiam ipsius corporum naturae pertingent, quam qui altius at­que altius montis cacumen ascendendo coelum se tandem manu contrectatures esse sibi per­sua­de­rent.

Igitur qua se plerique in rebus physicis commode vacare posse autumant, sola hic adminiculo est et lumen accendit metaphysica. Corpora enim constant par­ti­bus; quibus quomodo sint con­fla­ta, utrum sola partium pri­mi­ti­va­rum compraesentia, an virium mutuo conflictu repleant spa­tium, haud parvi sane interest, ut dilucide exponatur. Sed quo tandem pacto hoc in negotio metaphysicam geo­met­riae conciliare licet, cum gryphes facilius equis, quam philosophia transcendentalis geo­met­riae jungi posse videantur? Etenim cum illa spa­tium in infinitum divisibile esse praefracte neget, haec eadem, qua cetera solet, certitudine asseverat. Haec vacuum spa­tium ad motus liberos necessarium esse con­ten­dit, illa explodit. Haec attractionem s. sive gravitatem universalem a causis me­cha­ni­cis vix ex­pli­ca­bi­lem, sed ab insitis corporum in quiete et in distans agentium viribus proficiscentem com­mon­strat, illa inter vana imaginationis ludibria ablegat.

Quam licet cum componere haud parvi laboris esse appareat, saltem aliquid operae in eo collocare statui; aliis, quorum vires magis sufficiunt huic negotio, ad ea perficienda invitatis, quae hic solum afficere satagam.

Coronidis loco tantum addo: cum principium omnium internarum actionum s. sic vim elementorum in­si­tam motricem esse ne­ces­se sit, et extrinsecus quidem applicatam, quoniam illa praesens est ex­ter­nis, nec aliam ad movenda compraesentia vim concipere possimus, nisi quae illa vel repellere vel trahere conatur, neque porro posita sola vi repellente, elementorum ad componenda corpora col­li­ga­tio, sed dissipatio potius, sola autem attrahente col­li­ga­tio quidem, non vero extensio definita ac spa­tium intelligi queat, in antecessum jam quodammodo intelligi posse, qui bina haec principia ex ipsa elementorum natura et primitivia affectionibus deducere valet, eum ad explandam in­te­rio­rem corporum naturam non contemnendi momenti operam contulisse.

Monadologiae phy­si­cae.

Sectio I.

Monadum physicarum exsistentiam geo­met­riae consentaneam declarans.

Prop. I.
Definitio.

Substantia simplex, monas *) dicta, est, quae non constat pluralitate partium, quarum una absque aliis separatim exsistere potest.

*) Quoniam instituti mei ratio est, non nisi de ea simplicium sub­stan­tia­rum classe commentandi, quae corporum primitvae sunt partes, me inposterum terminis, sub­stan­tia­rum simplicium, monadum elementorum materiae, partium corporis pri­mi­ti­va­rum tanquam synonymis usurum, in antecessum moneo.

Prop. II.

Theorema. Corpora constant monadibus.

Corpora constant par­ti­bus, quae a se invicem separate perdurabilem habent exsistentiam. Quo­niam autem talibus par­ti­bus com­po­si­tio non est nisi relatio, hinc determinatio in se contingens, quae salva ipsarum exsistentia tolli potest, patet, com­po­si­tio­nem omnem corporis abrogari posse, su­per­stiti­bus nihilo secius par­ti­bus omnibus, quae antea erant compositae, com­po­si­tio­ne autem omni sub­lata, quae supersunt partes plane non habent com­po­si­tio­nem, atque adeo pluralitate sub­stan­tia­rum plane sunt destitutae, hinc simplices. Corpus ergo quodvis constat par­ti­bus primitivis absolute sim­pli­ci­bus, h. e. hic est monadibus.

SCHOLION. Consulto in demonstra­tio­ne praesenti celebratum illud rationis principium omittens, institutum e communi cui nemo non subscribit philosophorum, notionum adunatione confeci, sub­ve­ri­tus, ne quorum animi ab hoc principio sunt alieni, tali ra­tio­ne minus convineantur.

Prop. III.

Theorema. Spa­tium, quod corpora implent, est in infinitum divisibile, neque igitur constat par­ti­bus primitivis atque sim­pli­ci­bus.

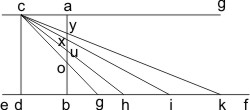Data linea ef indefinite producta, h. e. hic est ita, ut ulterius semper pro lubitu produci possit, alia ab, physica, h. e. hic est si ita arridet, par­ti­bus materiae primitivis con­fla­ta insistat ipsi ad angulos rectos. Ad latus alia erecta sit, cd, priori aequalis et similiter, posita, quod fieri posse non solum sensu geometrico, sed et physico non infitiaberis. Notentur in linea ef puncta quaelibet, g, h, i, k, et sic in indefinitum. Primo nemo in dubium vocabit, inter duo quaevis puncta seu si mavis mo­na­des datas lineam rectam physicam duci posse. Sit itaque ducta cg, et locus, ubi haec intersecat perpendicularem, ab, erit o. Jam ducta concipiatur alia linea physica inter puncta c et h, et erit locus u, ambabus lineis ch et ab communis, puncto a propior. Sicque porro, ductis ex eodem puncto c ad quaevis in linea ef, in infinitum producta, puncta i, k etc., semper puncta inter­sec­tio­nis, x, y, etc. propinquiora fient puncto a, ut vel geo­met­riae plane ignaro per se liquet. Et si putas lineas hasce physicas tandem justo arctiores sibi contiguas fore, ut juxta se consistere non possint, inferiores ductae auferri possunt. Et nihilo minus patet, loca inter­sec­tio­nis puncto a magis magisque appropinquare debere *), prouti in linea indefinite ef longinquius atque longinquius puntum no­ta­veris. Quae vero longinquitas quia in infinitum prorogari potest, appropinquatio etiam inter­sec­tio­nis versus punctum a infinitis incrementi par­ti­bus augescere potest. Neque vero unquam inter­sec­tio hoc pacto in punctum a cadet; quippe punctis c et a aequaliter distantibus a linea ef, linea, puncta c et a jungens et quousque libet continuata, semper tantundem distabit a subjecta linea ef, neque huic unquam occurrere potest, quod contra hypothesin. Adeoque continua di­vi­sio­ne lineae oa nunquam pervenitur ad partes primitivas non ulterius dividendas, h. e. hic est spa­tium est in infinitum divisibile, nec constat par­ti­bus sim­pli­ci­bus.

*) Neque unquam puncta y et x coincidere possunt, quia alias lineae cy et cx aeque coinciderent, et coincideret linea ck lineae ci, quod contra postulata.

Scholion. Demonstra­tio­nem hanc a permultis physicorum jam usurpatam huc allegavi, et quantum maxima fieri potuit perspicuitate ad physicum spa­tium accommodavi, ne, qui generali de di­ver­sita­te spatiorum geometrici et naturalis discrimine utuntur, exceptione quadam elabantur. Sunt quidem et aliae ejusdem sententiae demonstra­tio­nes in promptu, quarum ut unicam allegem, tri­an­gu­lum aequilaterum e monadibus, si ita arridet, constructum concipe, cujus si duo latera pro­du­can­tur in indefinitum, inque hisce sumseris distantias duplo, triplo, quintuplo, centuplo, etc. lateribus trianguli dati majores, harum estremitates lineis physicis jungi possunt, quae erunt in eadem ra­tio­ne, ut illae, tertio trianguli latere majores tantundemque pluribus simplicissimis constabunt. Quia vero inter quamlibet harum monadum, atque eam, quae in vertice anguli constituta est, lineae phy­si­cae ductae concipi possunt, hae basin trianguli dati infinities dividunt, adeoque spatii di­visi­bi­li­ta­tem infinitam egregie tuentur. Sed qui demonstra­tio­nem superius allatam absque prae­judi­cata­rum opinionum impedimentis perspexerit, omnibus aliis vacare meo quidem judicio potest.

Prop. IV.

Theorema. Compositum in infinitum divisibile non constat par­ti­bus primitivis s. sive sim­pli­ci­bus.

Cum in composito in infinitum divisibili nunquam perveniatur dividendo in partes omni com­po­si­tio­ne exutas, quae autem dividendo non tolli potest com­po­si­tio, tolli plane non possit nisi omnem compositi existentiam abrogaveris; quia vero, quae in composito remanent com­po­si­tio­ne omni sub­lata, partes audiunt simplices Prop. I; compositum infinities divisibile talibus non constare liquet.

Scholion. Non alie­num fore ab instituti ra­tio­ne autumavi, post vindicatas corpori cuilibet partes primitivas simplices, et post assertam infinitam spatii sui di­vi­sio­nem, cavere, ne quisquam mo­na­des pro infinite parvis corporis particulis habeat. Etenim spa­tium, quod est substantialitatis plane expers et relationis externae unitarum monadum phaenomenon, vel in infinitum continuata di­vi­sio­ne plane non exhauriri, abunde hoc pacto patescit; in quocunque autem composito com­po­si­tio est non nisi accidens, et sunt substantialia com­po­si­tionis subjecta, illud infinitam pati di­vi­sio­nem absonum est. Inde enim etiam sequeretur, partem quamlibet corporis primitivam ita esse com­pa­ra­tam, ut nec mille aliis, nec myriadibus, nec millionum millionibus, uno verbo, non, quotcunque as­sig­nare libuerit, iuncta particulam quamlibet materiae constituat, quod certe haud obscure omnem substantialitatem compositi tollit, neque itaque in corpora naturae cadere potest.

Corollarium. Corpus igitur quodlibet definito constat elementorum simplicium numero.

Prop. V.

Theorema. Quodlibet corporis elementum simplex, s. sive monas, non solum est in spatio, sed et implet spa­tium, salva nihilo minus ipsius simplicitate.

Cum corpus quodlibet definito conflatum sit elementorum simplicium numero, spa­tium vero, quod implet, infinitam patiatur di­vi­sio­nem, quodlibet horum elementorum partem spatii occupabit ulterius adhuc divisibilem, h. e. hic est spa­tium assignabile implebit.

Cum vero divisio spatii non sit separatio eorum, quorum unum ab alio semotum propriam habet sibique sufficientem exsistentiam, sed non nisi pluralitatem seu quantitatem quandam in externa relatione arguat, patet non inde pluralitatem partium sub­stan­tia­lium consequi; quae cum sola simplicitati monadis substantiali contrarietur, di­visi­bi­li­ta­tem spatii simplicitati monadis non adversari affatim patet.

Scholion. Non alia certe in disquisitione elementorum magis obstitit geo­met­riae cum metaphysica connubio sententia, quam praeconcepta illa, quamvis non satis examinata opinio, ac si divisibilitas spatii, quod elementum occupat, elementi etiam ipsius in partes substantiales di­vi­sio­nem argueret. Quod usque adeo extra dubitationis aleam positum esse vulgo autumatum est, ut, qui spatii realis di­vi­sio­nem infinitam tuentur, a monadibus quoque toto coelo abhorrerent, et qui monadibus subscribunt, spatii geometrici affectiones pro imaginariis habere, suarum partium rati sint. Verum cum e supra demonstratis aperte liqueat, nec geometram falli, nec quae apud metaphysicum residet, sententiam a vero aberrare, hanc, quae utrosque diremit opinionem, ac si elementum quoad substantiam absolute simplex spa­tium salva sua simplicitate implere non possit, utique falli ne­ces­se est. Quae enim spatiolum quoddam bifariam dividit linea aut superficies, partem spatii unam utique extra aliam exsistere indigitat. Quia vero spa­tium non est substantia, sed est quoddam externae sub­stan­tia­rum relationis phaenomenon, unius ejusdemque substantiae relationem bifariam dividi posse, simplicitati vel si mavis unitati substantiae non contrariatur. Quod enim est ab utraque lineae dividentis parte, non est quicquam a substantia ita separabile, ut ab ipso etiam semotum propriam exsistentiam tueatur, quod ad di­vi­sio­nem realem, quae tollit simplicitatem, utique requiritur, sed est unius ejusdemque substantiae utrinque exercita actio s. sive relatio, in qua quidem aliquam pluralitatem invenire non est substantiam ipsam in partes divellere.

Prop. VI.

Theorema. Monas spatiolum praesentiae suae definit non pluralitate partium suarum sub­stan­tia­lium, sed sphaera activitatis, quae externas utrinque sibi praesentes arcet ab ulteriori ad se invicem app­ro­pin­qua­tione.

Cum in monade non adsit pluralitas sub­stan­tia­rum, interim tamen quaevis solitario posita spa­tium repleat, per praec. praecedentum ratio spatii repleti non in positione substantiae sola, sed in ipsius respectu ex­ter­na­rum relatione quaerenda erit. Quia vero spa­tium replendo utrinque sibi immediate praesentes ab ulteriori arcet ad se invicem app­ro­pin­qua­tione, adeoque in ipsarum positu quidquam determinat, mensuram nempe propinquitatis, ad quam ipsa sibi accedere possunt, limitando, actionem exserere patet et quidem in spatio quaquaversum determinato, hinc spa­tium hoc sphaera activitatis suae replere concedendum est.

Prop. VII.

Problema. Spa­tium, quod quaelibet monas sphaera activitatis suae occupat, salva ipsius simplicitate, ulterius a difficultatibus vindicare.

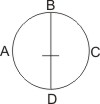Si monas quemadmodum contendimus spa­tium definitum implet, illud quovis alio finite exprimi poterit. Repraesentat igitur circulus ABCD spatiolum, quod monas occupat activitate sua, erit BD diameter sphaerae hujus activitatis h. e. hic est distantia, ad quam alia, ipsi in B et D praesentia, arcet ab ulteriori ad se invicem app­ro­pin­qua­tione. Verum ideo cave dixeris, hanc esse diametrum ipsius monadis, quod utique absonum foret. Neque etiam quidquam a sententia nostra magis est alie­num. Etenim cum spa­tium solis ex­ter­nis respectibus absolvatur, quodcunque sub­sta­tiae est internum, h. e. hic est substantia ipsa, ex­ter­na­rum determinationem sub­jec­tum, proprie non definitur spatio, sed quae ipsius determinationum ad externa referuntur, ea tantummodo in spatio quaerere fas est. At, ais, in hoc spatiolo adest substantia, et ubique in eodem praesto est; igitur qui dividit substantiam? Respondeo: spa­tium hoc ipsum est ambitus externae hujus elementi praesentiae. Qui itaque dividit spa­tium, quantitatem extensivam praesentiae suae dividit. At sunt praeter praesentiam externam h. e. hic est determinationes substantiae respectivas aliae internae, quae nisi forent, non haberent illae, cui inhaerent, sub­jec­tum. Sed internae non sunt in spatio, propterea quia sunt internae. Neque itaque di­vi­sio­ne ex­ter­na­rum determinationum ipsae dividuntur. Pariter ac si dixeris: Deus omnibus rebus creatis per actum conservationis interne praesto est, qui itaque dividit congeriem rerum creatarum, dividit Deum, quia ambitum praesentiae suae dividit; quo magis absonum dici quidquam non potest. Monas itaque, quae est elementum corporis primitivum, quatenus spa­tium implet, utique quidem quondam habet quantitatem extensivam, nempe ambitum activitatis, in quo vero non reperies plura, quorum unum ab alio separatum, h. e. hic est absque alio sibi solitarium, propriam habeat perdurabilitatem. Nam quod in spatio BCD reperitur, ab illo, quod adest in spatio BAD, separari ita non potest, ut quodlibet per se existat; quia utrumque non est, nisi determinatio unius ejusdemque substantiae externa; sed accidentia non existunt absque suis substantiis. *)

*) Difficultatum omnium, quae sententiae nostrae officere possunt, gravissima videtur, quae ab extrapositione determinationum unius ejusdemque substantiae depromta est. Etenim actio monadis, quae est in spatio BCD, est extra actionem, quae est in spatio BDA; ergo videntur realiter a se invicem diversa atque extra substantiam reperiunda. Verum relationes semper sunt et extra se invicem et extra substantiam, quia entia illa, ad quae refertur substantia, sunt a substantia et a se invicem realiter diversa, neque hoc pluralitatem substantialem arguit.

Prop. VIII.

Theorema. Vis, qua elementum corporis simplex spa­tium suum occupat, est eadem, quam vocant alias impenetrabilitatem; neque si ab illa vi discesseris, huic locus esse potest.

Impenetrabilitas est ea corporis affectio, qua contigua a spatio, quod occupat, arcet. Cum vero e praecedentibus innotuerit, spa­tium, quod corpus occupat, (si partes ipsius absque vacuo intermisto quam proxime sibi adunatas concipias,) conflatum esse spatiolis, quae singula elementa simplicia implent; cum porro ad arcenda irruentia in spa­tium replentum corpora externa s. sive ad impenetrabilitatem requiratur renitentia atque adeo vis quaedam, in prioribus autem demonstratum sit, elementa spa­tium suum definitum replere activitate quadam alia eo penetratura arcendi; patet impenetrabilitatem corporum non ab alia nisi eadem illa naturali elementorum vi pendere. Quod erat primum.

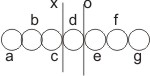Deinde sit linea ag elementis materiae primitivis, h. e. hic est monadibus con­fla­ta, si elementum quodvis d per substantiae suae praesentiam non nisi locum designaret neque occuparet spa­tium, locus d lineam datam ag bisecaret, et quia itaque notat, ubi dimidium alterum lineae desinit al­ter­um­que incipit, erit utrique dimidio lineae communis. Sed non sunt lineae phy­si­cae aequales, nisi aequali constent elementorum numero et non est par utrinque elementorum numerus, nisi in linea ac et eg; ergo locus monadis d erit lineis ac, eg, communis, h. e. hic est lineae dictae immediate sibi in loco nominato occurrent neque itaque elementum d proximas e et c arcet ab immediato contactu, h. e. hic est non erit impenetrabile. Si negas itaque locum a monade d occupatum esse communem lineis ac, eg, erit punctum x, ubi lineae ac et dg sibi immediate occurrunt et o, in quo sibi occurrunt lineae ad et eg; quia itaque locus monadis d diversus est a loco x itemque a loco o, quoniam alias immediato contactui communis semper locus esset, ut antea dictum, habes tria loca diversa x, d, o, quae procul dubio lineam quondam definiunt. Definitur igitur immediata praesentia monadis d linea definita, h. e. hic est in spatio definito praesto est, et quia per solam substantiae positionem non spa­tium, sed locum occupare posset, adsit ne­ces­se est aliud quiddam in subtantia, quod determinat propinquitatis in elementis utrinque contingentibus mensuram et vim quamlibet a propieri accessu elementorum c et e arcet; sed vi non potest opponi nisi vis; ergo eadem vis, qua elementum corporis spa­tium suum occupat, causat impenetrabiltatem. Quod erat alterum.

Sectio II.

Affectiones monadum physicarum generalissimas, quatenus in diversis diversae ad naturam corporum intelligendam faciunt, explicans.

Prop. IX.
Definitio.

Contactus est virium penetrabilitatis plurium elementorum sibi invicem facta applicatio.

Scholion. Contactus vulgo per immediatam praesentiam definitur. Sed si vel maxime externam adjiceres, (quoniam sine hoc additamento Deus, qui omnibus rebus immediate, sed intime praesens est, ipsas contingere putandus foret,) tamen omnibus numeris absoluta vix erit definitio. Etenim quoniam satis ab aliis evictum, corpora vacuo spatio disterminata nihilominus coexsistere posse, ideoque et immediate sibi praesentia esse, quanquam, absque contactu mutuo, procul dubio hic vitii tenebitur definitio. Porro non sine magna veri specie a Newtoni schola immediata corporum etiam a se dissitorum attractio defenditur, quorum tamen compraesentia absque contactu mutuo succederet. Praeterea si definitionem tueris, quae immediatam compraesentiam pro ipsa contactus notione venditat, explicanda tibi primum est praesentiae hujus notio. Si, ut fit, declaras per mutuam actionem; in quoniam quaeso constitit actio? Procul dubio corpora in se movendo agunt. Vis motrix vero e puncto dato exserta aut repellit alia ab eodem aut trahit. Ultra actio in contactu intelligenda sit, facile patescit. Corpus enim corpori propius propiusque admovendo tum dicimus invicem se contingere, cum sentitur vis impenetrabilitatis h. e. hic est repulsionis. Ergo huius adversus se invicem facta a diversis elementis actio atque reactio genuinam efficit contactus notionem.

Prop. X.

Theorema. Corpora per vim solum impenetrabilitatis non gauderent definito volumine, nisi adforet alia pariter insita attractionis, cum illa conjunctim limitem definiens extensionis.

Vis impenetrabilitatis est vis repulsiva, externa quaevis ab app­ro­pin­qua­tione ulteriori arcens. Cum haec vis sit cuilibet elemento ingenita, ex ipsius natura intelligi quidem poterit, cur pro distantiae, ad quam extenditur, augmentis intensitas actionis diminuatur quod in distantia quavis data plane nulla sit, intelligi plane per se non potest. Ideoque apud hanc solam si steterit, corporum compages plane nulla foret, quippe repellentibus se modo particulis, corporique nullum constaret volumen definito limite circumscriptum. Ne­ces­se igitur est, ut opponatur huic conatui alius oppositus, et in data distantia aequalis, limitem spatio occupando determinans. Qui cum repulsioni ex adversum agat, est attractio. Opus igitur est cuilibet elemento praeter vim impenetrabilitatis alia attractiva, a qua si discesseris, non resultarent determinata corporum naturae volumina.

Scholion. Ambarum virium tam repulsionis quam attractivae quae sint in elementis leges indagare, ardui sane momenti est investigatio et digna, quae ingenia exerceat perspicaciora. Mihi hic loci sufficit earum existentiam, quantum per brevitatis legem licuit, certissime evictam reddidisse. Sed si veluti e longinquo quaedam ad hanc quaestionem pertinentia prospicere arridet, nonne, cum vis repulsiva e puncto intimo spatii, ab elemento occupati, extrorsum agat, intensitas illius censenda erit secundum spatii, in quod extenditur, augmentum reciproce debilitari? Non potest enim vis e puncto distributa in sphaera definita efficax deprehendi, nisi totum, quod comprehenditur sub dato diametro spa­tium, agendo impleat. Quod hac ra­tio­ne patefit. Si enim vim concipias secundum lineas rectas e data superficie emanantem, sicuti lucem, seu etiam secundum Keilii mentem ipsam vim attractionis, erit vis hac ra­tio­ne exercita in ra­tio­ne multitudinis linearum, quae ex hac superficie duci possunt, hoc est in ra­tio­ne ipsius superficiei agentis. Adeoque si superficies sit infinite parva, erit etiam haec vis infinite parva, et si tandem sit punctum, plane nulla. Ideoque per lineas divergentes, e puncto non potest vis diffundi in certa distantia assignabilis. Neque ideo deprehendetur efficax, nisi implendo totum, in quo agit, spa­tium. Sed spatia sphaerica sunt, ut cubi distantiarum. Ergo cum eadem vis per majus spatium diffusa diminuatur pro ra­tio­ne inversa spatiorum, erit vis impenetrabilitatis in ra­tio­ne triplicata distantiarum a centro praesentiae reciproce.

Contra ea cum attractio sit quidem ejusdem elementi actio, sed in oppositum versa, erit superficies sphaerica, in quam in data distantia exercetur attractio, terminus a quo; cujus cum punctorum, a quibus in centrum tendentiae lineae duci possunt, multitudo, atque adeo attractionis quantitas definita sit, erit hoc pacto assignabilis, et decrescens in ra­tio­ne inversa superficierum sphaericarum, i. e, id est in inversa duplicate distantiarum.

Si igitur repulsiva in subtriplicata, adeoque longe majori ra­tio­ne decrescere statuatur, in aliquo diametri puncto aequales esse attractionem et repulsionem ne­ces­se est. Et hoc punctum determinabit limitem impenetrabilitatis, et contactus externi ambitum s. sive volumen; victa enim attractione vis repulsiva ulterius non agit.

Corollarium. Si hanc virium insitarum legem ratam habes, agnosces etiam omnium elementorum, quantumvis diversae speciei, aequale volumen. Etenim cum sit in aprico, vires repulsionis pariter ac attractivas, quoniam diversis maxime esse posse diversas, hic intensiores, alibi remissiores, tamen, quoniam vis dupla repulsionis est in eadem distantia dupla, et vis attractionis stidem [itidem Druckfehler?], et congruum sit, vires omnes elementi motrices, quod est specifice duplo fortius, esse in ra­tio­ne eadem fortiores, semper vires nominatae in eadem distantia aequari, adeoque aequale volumen elementi determinare ne­ces­se est, quantumcunque, a viribus cognominibus aliorum elementorum gradu differant.

Prop. XI.

Theorema. Vis inertiae est in quolibet elemento quantitatis definitae, quae in diversis poterit esse, maxime diversa.

Corpus motum in aliud incurrens nulla polleret efficacis, et infinite parvo quovis obstaculo redigeretur ad quietem, nisi gauderet vi inertiae, qua in statu movendi perseverare annititur. Est vero vis inertiae corporis summa virium inertiae omnium elementorum, ex quibus conflatum est, (et hanc quidem vocant massam;) ergo quodlibet elementum certa celeritate motum, nisi haec multiplicetur per vim inertiae, nulla plane polleret movendi efficacia. Quodcunque autem in aliud multiplicando dat quantum, altero factorum majus, ipsum est quantitas, quae tum major, tum minor alia assignari poterit. Ergo vi inertiae cujuslibet elementi alia vel major vel minor dari poterit in diversae speciei elementis.

Coroll. I. Dari possunt elementis quibuslibet datis alia, quarum vis inertiae, s. sive quod diverso respectu idem est, vis motrix, duplo vel triplo major est, h. e. hic est quae et certae celeritati duplo vel triplo majori vi resistunt, et eadem celeritate mota duplo vel triplo majori pollent impetu.

Corrol. II. Cum elementa quaelibet, quantumvis diversae speciei, pari tamen volumine pollere constet e coroll. prop. praec. corollario proposito praecedente, adeoque pari spatio exacte repleto parem semper contineri elementorum numerum, hinc recte concluditur: corpora, si vel maxime a vacui admistione discesseris et totum spa­tium perfecte adimpletum sumseris, tamen sub eodem volumine diversissimas massas continere posse, quippe elementis majori vel minori vi inertiae praeditis. Nam massa corporum non est, nisi ipsorum vis inertiae quantitas, qua vel motui resistunt vel data celeritate mota certo movendi impetu pollent.

Hinc a minore materiae, sub dato volumine comprehensae, quantitate ad minorem densitatem et ad majora interstitia vacua intercepta non semper satis firma valet consequentia. Utrumque corpus potest vel paribus interstitiis vacuis pollere, vel perfecte densum esse, et nihilo minus alterutrum longe majori massa pollere; diversitatis causa plane in ipsa elementorum natura residente.

Prop. XII.

Theorema. Diversitas specifica densitatis corporum, in mundo observabilium, absque di­ver­sita­te specifica inertiae ipsorum elementorum explicari plane non potest.

Si elementa omnia pari gauderent vi inertiae parique volumine, ad intelligendam corporum raritatis differentiam opus est vacuo absoluto, par­ti­bus intermisto. Neque enim secundum Newtoni, Keilii aliorumque demonstra­tio­nes in medio, tali ra­tio­ne perfecte impleto, motui libero locus est. Ideoque ad explicandam mediorum infinite diversam densitatem specificam, e. g. exemplum gratuit aetheris, aeris, aquae, auri, indulgendum est immodicae conjectandi libidini, qua, quae ab hominum intelligentia maxime remota est, ipsa elementorum textura temere pro lubitu confingitur, mox bullularum tenuissimarum, mox ramorum et spirarum contortarum instar eam libere et audacter concipiendo, quo materiam mirie modis distentam et exigua materis ingens spa­tium complexam cogitare possis. Sed accipe, quae adversum pugnant ra­tio­nes.

Fibrillae illae immensum quantum exiles, aut bullulae, quae sub cuticula immensae tenuitatis ingens pro quantitate materiae vacuum comprehendunt, ne­ces­se est, ut continuo corporum conflictu et attritione tandem conterantur, et hac ra­tio­ne comminutarum ramenta spa­tium vacuum interceptum tandem oppleant. Quo facto spa­tium mundanum unquaque perfecte plenum valida inertia obtorpescet, motusque omnes brevi reducentur ad quietem.

Porro cum secundum sententiam talem media specifice rariora par­ti­bus maxime distentis et magno volumine praeditis constare opus sit, quo tandem pacto illis interstitia corporum densiorum, quae secundum eandem sententiam arctiora sunt, pervia esse possunt, quemadmodum ignem, fluidum magneticum, electricum corpora permeare facillime constat? Nam, particulae majori volumine praeditae quomodo in interstitia, ipsis angustiora, semet penetrare possint, juxta cum ignarissimis ignoro.

Nisi itaque diversitas specifica ipsorum simplicissimorum elementorum, qua, eodem spatio exacte repleto, nunc minor, nunc longe major massa construi poterit, concedatur, physica semper ad hanc difficultatem veluti ad scopulum haerebit.

Prop. XIII.

Theorema. Elementa corporis, etiam solitario posita, perfecta gaudent vi elastica in diversis diversa, et constituunt medium in se et absque vacuo admisto primitive elasticum.

Elementa singula simplicia spa­tium praesentiae suae occupant vi quadam definita, externas substantias ab eodem arcente. Cum vero vis quaelibet finita gradum habeat, ab alia majori superabilem, patet huic repulsivae aliam opponi posse fortiorem, cui cum in eadem distantia arcendae vis elementi ingenita non sufficiat, patet illam in spa­tium ab ipso occupatum aliquatenus penetraturam. Sed vires quaelibet e puncto definito in spa­tium exporrectae cum pro distantiae augmento debilitentur, vim hanc repulsivam, quo propius centro acceditur activitatis, eo et forties reagere patet. Et quoniam vis repellens, quae in data a centro repulsionis distantia finita est, in proportione definite appropinquationum crescit, ad punctum ipsum infinita sit ne­ces­se est, patet, per nullam vim cogitabilem elementum penitus penetrari posse. Erit igitur perfecte elasticum et plura ejusmodi junctis elasticitatibus constituent medium primitive elasticum. Quod haec elasticitas sit in diversis diversa e coroll. prop. X. patet.

Coroll. Elementa sunt perfecte impenetrabilia, hoc est, quantacunque vi externa spatio, quod occupant, penitus excludi nescia, sed sunt condensibilia, et corpora etiam talia constituunt, quippe concedentia aliquantulum vi externae comprimenti. Hinc origo corporum s. sive mediorum primitive elasticorum, in quibus aetherem s. sive materiam ignis in antecessum profiteri liceat.

Quelle

Immanuel Kant′s Sämtliche Werke. Fünfter Teil. Schriften zur Philosophie der Natur. Herausg. Karl Rosenkranz und Friedr. Wilh. Schubert. Leipzig Leopold Voss 1839.

© 2016 Dr. Rainer Stumpe