Verzeichnis der vorkommenden Worte mit Übersetzung
Der nicht übersetzte Text enthält noch OCR Fehler.
Dissertatio De Arte Combinatoria
In qua Ex Arithmeticae fundamentis Complicationum ac Transpositionum Doctrina novis praeceptis exstruitur, & usus ambarum per universum scientiarum orbem ostenditur; nova etiam Artis Meditandi, Seu Logicae Inventionis semina sparguntur.
Praefixa est Synopsis Tractatus, & additamenti loco Demonstratio Existentiae Dei, ad Mathematicam certitudinem exacta.
Autore
Gottfredo Guiliemo Leibnüzio
Lipsensi Phil. Magist. & J. U. Baccal.
Viro Summo, Magnifico, maxime reverendo, DNO Martino Geiero,
S. Stae. Theol. Doct. Serenissimi Electoris Saxoniae Supremo Concionatori Aulico, Supremi Dresdensis Consistorii Assessori, & Consiliario Ecclesiastico, Theologo Incomparabili:
suo vero, praeter susceptionis beneficium, Patrono & Mecoenati maximo, rationem studiorum suorum constare voluit.
Autor
Synopsis Dissertationis De Arte Combinatoria
Sedes Doctrinae istius Arithmetica. Hujus origo. Complexiones autem sunt Arithmeticae purae, situs figuratae. Definitiones novorum terminorum. Quid aliis debeamus. Problema I. dato numero & exponente Complexiones & in specie Combinationes invenire, Probl. II. dato numero complexiones simpliciter invenire. Horum usus (1.) in divisionis inveniendis speciebus: v. g. mandati, Elementorum, Numeri, Registrorum Organi Musici, Modorum Syllogisimi categorici, qui in universum sunt 512. Juxta Hospinianum, utiles 88 juxta nos. Novi modi figurarum ex Hospiniano: Barbari, Celaro, Camestres, & nostri Figurae IVtae Galenicae: Fresismo, Ditabis, Celanto, Colanto. Sturmii modi novi ex terminis infinitis, Daropti. Demonstratio Conversionum. De Complicationibus Figurarum in Geometria, congruis, hiantibus, texturis. Ars casus formandi in Jurisprudentiae. Theologia autem quasi species est Jurisprudentiae, de Jure nempe Publico in Republica DEI super homines. (2.) in inveniendis datarum specierum generibus subalternis, de modo probandi sufficientiam datae divisionis. (3.) Usus in inveniendis propositionibus & argumentis. De arte Combinatoria Lullii, Athanasii Kircheri, nostra, de qua sequentia: Duae sunt copulae in propositionibus: Revera, & non, seu + & -. De formandis praedicamentis artis Combinatoriae. Invenire: dato definito vel termino; definitiones, vel terminos aequipollentes: Dato subjecto praedicat in propositione HA, item PA, item N. Numerum classium, numerum Terminorum in Classibus: Dato capite complexiones: dato praedicato subjecta in Propositione UA, PA, & N. Datis duobus terminis in propositione necessaria UA & UN argumentum enta seu medios terminos invenire. De Locis Topicis, seu modo efficiendi & probandi propositiones contingentes. Specimen mirabile Praedicamentorum artis combinatoriae ex Geometria. Porisma de Scriptura Universali cuicunque legenti cujuscunque; linguae perito intelligibili, Dni de Breissac specimen artis com2natoriae seu meditandi in re bellica, cuique beneficio omnia consideratione digna Imperatori in mente veniant. De Usu rotarum concentricarum Chartacearum in arte hac. Serae hac arte constructae sine clavibus aperiendae 𝔐𝔞𝔥𝔩-𝔖𝔠𝔥𝔩𝔬𝔢𝔰𝔰𝔢𝔯 / Mixturae Colorum. Probl. III. Dato numero Classium & rerum in singulis, complexiones classium invenire. Divisionem in divisionem ducere, de vulgari Conscientiae divisione. Numerus sectarum de summo Bono e Varrone apud Augustinum. Ejus Examen. In dato gradu Consanguinitatis numerus (1.) cognationem juxta. l. 1. & 3. D. de Grad. & Aff. (2.) personarum juxta l0. D. eod. Singulari artificio inventus. Prob. IV. Dato numero rerum variationes ordinis invenire. Uti hospitum in mensa 6. Drexelio, 7. Harsdöffero, 12. Henischio. Versus Protei, v. g. Bauhusii, Lansii, Ebelii, Ricciolo, Harsdörfferi. Variationes literarum Alphabeti, comparatarum Atomis, Tesserae Grammaticae. Probl. V. Dato numero rerum variationem vicinitatis invenire. Locus honoratissimus in rotundo. Circulus Syllogisticus. Probl. VI. Dato numero rerum variandarum, quarum aliqua vel aliquae repetuntur, variationem ordinis invenire. Hexametrorum species 76. Hexametri 26. Quorum sequens antecedentem litera excedit Publilii Porphyrii Optatiani: quis ille. Diphtongi a Scriptura. Probl. VII. Reperire dato capite variationes. Probl. VIII. Variationes alteri dato capiti communes. IX. Capita variationes communes habentia. X. Capita variationum utilium & inutilium. Probl. XI. Variationes inutiles. XII. Utiles. Optatiani Proteus versus (Virgilii Casualis) J. C. Scaligeri (Virgilii Casualis) Bauhusii (Ovidii Casualis.) Kleppisii (praxis comparandi Variationes inutiles & utiles) Caroli a Goldstein / Reimeri C. L. Daumii 4, quorum ultimi duo plusquam Protei.
zur Übersetzung des Abschnitts
Additamentum: Demonstratio Existentiae Dei.
…
Prooemium.
Cum Deo!
Metaphysica, ut altissime ordiar, agit tum de Ente, tum de Entis affectionibus; ut autem corporis naturalis affectiones non sunt corpora, ita Entis affectiones non sunt Entia.
Est autem Entis affectio (seu modus) alia absoluta, quae dicitur Qualitas, alia respectiva, eaque vel rei ad partem suam, si habet, Quantitas, vel rei ad aliam rem, Relatio, etsi accuratius loquendo, supponendo partem quasi a toto diversam, etiam quantitas rei ad partem relatio est. Manifestum igitur, neque Qualitatem, neque Quantitatem, neque Relationem Entia esse:
Earum vero tractationem in actu signato ad Metaphysicam pertinere.
Porro omnis Relatio aut est Unio aut Convenientia. In unione autem Res, inter quas haec relatio est, dicuntur partes, sumtae cum unione, Totum. Hoc contingit, quoties plura simul tanquam Unum supponimus. Unum autem esse intelligitur, quicquid uno actu intellectus seu simul cogitamus, v. g. quemadmodum numerum aliquem quantumlibet magnum saepe Caeca quadam cogitatione simul apprehendimus, cyphras nempe in charta legendo, cui explicate intuendo ne Mathusalae quidem aetas suffectura sit.
Abstractum autem ab uno est Unitas, ipsumque totum abstractum ex unitatibus seu totalitas dicitur Numerus. Quantitas igitur est Numerus partium. Hinc manifestum, in re ipsa Quantitatem et Numerum coincidere, illam tamen interdum quasi extrinsece, relatione seu Ratione ad aliud, in subsidium nempe quamdiu numerus partium cognitus non est, exponi.
Et haec origo est ingeniosae Analyticae Speciosae, quam excoluit inprimis Cartesius, postea in praecepta collegere Franc. Schottenius, et Erasmius Bartholinus, hic elementis Matheseos universalis, ut vocat. Est igitur Analysis doctrina de Rationibus et Proportionibus, seu Quantitate non exposita; Arithmetica de Quantitate exposita seu Numeris: falso autem Scholastici credidere Numerum ex sola divisione continui oriri nec ad incorporea applicari posse. Est enim numerus quasi figura quaedam incorporea, orta ex Unione Entium quorumcunque, v. g. DEI, Angeli, Hominis, Motus, qui simul sunt quatuor.
Cum igitur Numerus sit quiddam Universalissimum, merito ad Metaphysicam pertinet, si Metaphysicam accipias pro doctrina eorum, quae omni entium generi sunt communia. Mathesis enim (ut nunc nomen illud accipitur) accurate loquendo non est una disciplina, sed ex variis disciplinis decerptae particulae quantitatem subjecti in unaquaque tractantes, quae in unum propter cognationem merito coaluerunt. Nam uti Arithmetica atque Analysis agunt de Quantitate Entium, ita Geometria de Quantitate corporum, aut spatii quod corporibus coextensum est. Politicam vero disciplinarum in professiones divisionem, quae commoditatem docendi potius, quam ordinem naturae secuta est, absit ut convellamus.
Caeterum Totum ipsum (et ita Numerus vel Totalitas) discerpi in partes tanquam minora tota potest, id fundamentum est Complexionum, dummodo intelligas dari in ipsis diversis minoribus totis partes communes, v. g. Totum sit A B C, erunt minora tota, partes illius, AB, BC, AC: et ipsa minimarum partium, seu pro minimis suppositarum (nempe Unitatum) dispositio inter se et cum toto, quae appellatur situs, potest variari. Ita oriuntur duo Variationum genera, Complexionis et Situs.
Et tum Complexio, tum Situs ad Metaphysicam pertinet, nempe ad doctrinam de Toto et partibus, si in se spectentur; si vero intueamur Variabilitatem, id est Quantitatem variationis, ad numeros et Arithmeticam deveniendum est. Complexionis autem doctrinam magis ad Arithmeticam puram, situs ad figuratam pertinere crediderim, sic enim unitates lineam efficere intelliguntur. Quamquam hic obiter notare volo, unitates vel per modum lineae rectae vel circuli aut alterius lineae linearumve in se redeuntium aut figuram claudentium disponi posse, priori modo in situ absoluto seu partium cum toto, Ordine; posteriori in situ relato seu partium ad partes, Vicinitate, quae quomodo differant infra dicemus def. 4 et 5. Haec prooemii loco sufficiant, ut qua in disciplina materiae hujus aedes sit, fiat manifestum.
zur Übersetzung des Abschnitts
Definitiones.
- Variatio h. l. est mutatio relationis. Mutatio enim alia substantiae est alia quantitatis alia qualitatis; alia nihil in re mutat, sed solum respectum, situm, conjunctionem cum alio aliquo.
- Variabilitas est ipsa quantitas omnium Variationum. Termini enim potentiarum in abstracto sumti quantitatem earum denotant, ita enim in Mechanicis frequenter loquuntur potentias machinarum duarum duplas esse invicem.
- Situs est localitas partium.
- Situs est vel absolutus vel relatus: ille partium cum toto, hic partium ad partes. In illo spectatur numerus locorum & distantia ab initio & fine, in hoc neque initium neque finis intelligitur, sed spectatur tantum distantia partis a data parte. Hinc ille exprimitur linea aut lineis figuram non claudentibus neque in se redeuntibus, & optime linea recta; hic linea aut lineis figuram claudentibus, & optime circulo. In illo prioritatis & posterioritatis ratio habetur maxima, in hoc nulla. Illum igitur Optime ordinem dixeris;
- Hunc vicinitatem, illum dispositionem, hunc compositionem. Igitur ratione ordinis differunt situs sequentes: abcd. bcda. cdab. dabc. At in Vicinitate nulla variatio sed unus situs esse intelligitur, hic nempe: Unde festivissimus Taubmannus, cum Decanus Facultatis philosophicae esset, dicitur Witebergae in publico programmate seriem candidatorum Magisterii circulari dispositione complexus, ne avidi lectores intelligerent, quis suillum locum teneret.
- Variabilitatem ordinis intelligemus fere, quando ponemus Variationes κατʹ έξοχήν v. g. Res IV possunt transponi modis 24.
- Variabilitatem complexionis dicimus Complexiones, v. g. Res IV modis diversis 15 invicem conjungi possunt.
- Numerum rerum variandarum dicemus simpliciter Numerum, v. g. IV in casu proposito.
- Complexio est Unio minoris Totius in majori, uti in prooemio declaravimus.
- Ut autem certa Complexio determinetur, majus totum dividendum est in partes aequales suppositas ut minimas (id est quae nunc quidem non ulterius dividantur), ex quibus componitur et quarum variatione variatur Complexio seu Totum minus; quia igitur totum ipsum minus, majus minusve est, prout plures partes una vice ingrediuntur, numerum simul ac semel conjungendarum partium seu unitatum dicemus Exponentem, exemplo progressionis geometricae. V. g. sit totum ABCD. Si tota minora constare debent ex 2 partibus, v. g. AB, AC, AD, BC, BD, CD, exponens erit 2; sin ex tribus, v. g. ABC, ABD, ACD, BCD, exponens erit 3.
- Dato exponente complexiones ita scribemus: si exponens ut 2, Com2nationem (combinationem); si 3, Com3snationem (conternationem); si 4 Con4nationem &c.
- Complexiones simpliciter sunt omnes complexiones omnium, Exponentium computatae, v. g. 15 (de 4 Numero) quae componitur ex 4 (Unione), 6 (com2natione), 4 (con3natione), 1 (con4natione).
- Variatio utilis (inutilis,) est quae propter materiam subjectam locum habere non potest, v. g. 4 Elementa com2nari possunt 6𝔪𝔞𝔥𝔩; sed duae com2nationes sunt inutiles, nempe quibus contrariae ignis, aqua; aer, terra com2nantur.
- Classis rerum est totum minus, constans ex rebus convenientibus in certo tertio, tanquam partibus, sic tamen ut reliquae classes contineant res contradistinctas, v. g. infra probl. 3, ubi de classibus opinionum circa summum Bonum ex B. Augustino agemus.
- Caput Variationis est positio certarum partium; Forma variationis, omnium, quae in pluribus variationibus obtinet, v. Infra Probl. 7.
- Variationes communes sunt, in quibus plura capita concurrunt, v. infra probl. 8 et 9.
- Res homogenea est quae est aeque dato loco ponibilis salvo capite, Monadica autem quae non habet homogeneam, v. probl. 7.
- Caput multiplicabile dicitur, cujus partes possunt variari.
- Res repetita est quae in eadem variatione saepius ponitur, v. Probl. 6.
- Signo + designamus additionem, — subtractionem, ᴖ multiplicationem, ᴗ divisionem, f. facit seu summam, = aequalitatem. In prioribus duobus et ultimo convenimus cum Cartesio, Algebraistis, aliisque; alia signa habet Isaacus Barrowius in sua editione Euclidis, Cantabrig. 8vo, anno 1655.
zur Übersetzung des Abschnitts
Problemata.
Tria sunt quae spectari debent: Problemata, Theoremata, usus; in singulis problematis usum adjecimus; sicubi operae pretium videbatur, & theoremata. Problematum autem quibusdam rationem solutionis addidimus. Ex iis partem posteriorem primi, secundum & quartum aliis debemus, reliqua ipsi eruimus. Quis illa primus detexerit ignoramus. Schwenterus Delic. I. l. sect. I. prop. 32. apud Hieronymum Cardanum, Johannem Buteonem, & Nicolaum Tartaleam extare dicit. In Cardani tamen Practica Arithmetica, quae prodiit Mediolani anno 1539, nihil reperimus. Inprimis dilucide, quicquid dudum habetur, proposuit Christoph. Clavius in Com. supra Joh. de Sacro Bosco Sphaer. Edit. Romae forma 4ta anno 1585 pag. 33·seqq.
zur Übersetzung des Abschnitts
Probl. I.
Dato numero et exponente complexiones inveniere.
Solutionis duo sunt modi, unus de omnibus complexiones, alter de combinationibus solum: ille quidem est generalior, hic vero pauciora requirit data, nempe numerum solum et exponentem, cum ille etiam praesupponat inventas complexiones antecedentes.
Generaliorem modum nos deteximus, specialis est vulgatus. Solutio illius talis est: "Addantur complexiones exponentis antecedentia et dati de numero antecedenti, productum erunt complexiones quaesitae"; v. g. esto numerus datus 4, exponens datus 3, addantur de numero antecedente 3 com2nationes 3 et con3natio l (3 + 1 f. 4), productum 4 erit quaesitum.
Sed cum praerequirantur complexiones numeri antecedentis, construenda est tabula אּ, in qua linea suprema a sinistra dextrorsum continet Numeros a 0 usque ad 12 utrimque inclusive, satis enim esse duximus huc usque progredi, quam facile est continuare; linea extrema sinistra a summo deorsum continet Exponentes a 0 ad 12, linea infima a sinistra dextrorsum continet Complexiones simpliciter.
Exponentes |
0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | Complexiones |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 n | 8 u | 9 m | 10 e | 11 r | 12 i | ||
| 2 | 0 | 0 | 1 | 3 | 6 | 10 | 15 | 21 | 28 | 36 | 45 | 55 | 66 | ||
| 3 | 0 | 0 | 0 | 1 | 4 | 10 | 20 | 35 | 56 | 84 | 120 | 165 | 220 | ||
| 4 | 0 | 0 | 0 | 0 | 1 | 5 | 15 | 35 | 70 | 126 | 210 | 330 | 495 | ||
| 5 | 0 | 0 | 0 | 0 | 0 | 1 | 6 | 21 | 56 | 126 | 252 | 462 | 792 | ||
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 7 | 28 | 84 | 210 | 462 | 924 | ||
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 8 | 36 | 120 | 330 | 792 | ||
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 9 | 45 | 165 | 495 | ||
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 10 | 55 | 220 | ||
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 11 | 66 | ||
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 12 | ||
| 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | ||
| * | 0 | 1 | 3 | 7 | 15 | 35 | 63 | 127 | 255 | 511 | 1023 | 2047 | 4095 | ||
| † | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 |
quae coincidunt cum terminis progressionis geometricae duplae †.
Reliquae inter has lineae continent complexiones dato numero qui sibi in vertice directe respondet, et exponente qui e regione sinistra. Ratio solutionis, et fundamentum Tabulae patebit, si demonstraverimus, Complexiones dati numeri et exponentis oriri ex summa complexionum de numero praecedenti exponentis et praecedentis et dati. Sit enim numerus datus 5, exponens datus 3, erit numerus antecedens 4; is habet con3nationes 4 per Tabulam אּ, com2nationes 6. Jam numerus 5 habet omnes com3nationes quas praecedens (in toto enim et pars continetur) nempe 4, et praeterea tot quot praecedens habet com2nationes, nova enim res qua numerus 5 excedit 4, addita singulis com2nationibus hujus, facit totidem novas con3nationes, nempe 6 + 4 f. 10. Ergo Complexiones dati numeri &c. Q. E. D.
Majoris lucis causa apponimus Tabulam ב, ubi lineis transversis distinximus Con3nationem de 3 et de 4 et de 5, sic tamen ut con3nationes priores sint sequenti communes, et per consequens tota tabula sit con3nationum numeri 5, utque manifestum esset, quae con3nationes numeri sequentis ex com2nationibus antecedentis addito singulis novo hospite orirentur, linea deorsum tendente combinationes a novo hospite distinximus.
|
Numerus Con3nationum
|
1 | ab | c | 3 |
| 2 | ab | d | Rerum |
|
| 3 | ac | d | ||
| 4 | bc | d | ||
| 5 | ab | e | 4 | |
| 6 | ac | e | ||
| 7 | ad | e | Numerus |
|
| 8 | bc | e | ||
| 9 | bd | e | ||
| 10 | cd | e | 5 |
Adjiciemus hic Theoremata quorum τό ὅτι ex ipsa tabula אּ manifestum est, τό δίοτι ex tabulae fundamento: 1) si exponens est major Numero, Complexio est 0. 2) Si aequalis, ea est 1. 3) Si exponens est Numero unitate minor, Complexio et Numerus sunt idem. 4) Generaliter: Exponentes duo, in quos numerus bisecari potest, seu qui sibi invicem complemento sunt ad numerum, easdem de illo numero habent complexiones. Nam cum in minimis exponentibus 1 et 2, in quos bisecatur numerus 3, id verum sit quasi casu, per tab. ח, et vero caeteri ex eorum additione oriantur per solut. probl. 1, si aequalibus (3 et 3) addas aequalia (superius 1 et inferius l), producta erunt aequalia (3+1 f. 4=4), et idem eveniet in caeteris necessitate. 5) Si numerus est impar, dantur in medio duae complexiones sibi proximae aequales; sin par, id non evenit. Nam numerus impar bisecari potest in duos exponentes proximos unitate distantes, v. g. 1+2 f. 3; par vero non potest. Sed proximi, in quos bisecari par potest, sunt iidem. Quia igitur in duos exponentes impar numerus bisecari potest, hinc duas habet Complexiones aequales per th. 4, quia illi unitate distant, proximas. 6) Complexiones crescunt usque ad exponentem numero ipsi dimidium aut duos dimidio proximos, inde iterum decrescunt. 7) Omnes numeri primi metiuntur suas complexiones particulares (seu dato exponente). 8) Omnes complexiones simpliciter sunt numeri impares.
| ab | ac | ad | ae | af |
| bc | bd | be | bf | |
| cd | ce | cf | ||
| de | df | |||
| ef |
Restat hujus Problematis altera pars quasi specialis: "dato Numero (A) com2nationes (B) invenire. Solutio. Ducatur numerus in proxime minorem, facti dimidium erit quaesitum, A ᴖ A - l ,,ᴗ 2 = B. Esto v. g. Numerus 6, 6ᴖ 5 f. 30 ᴗ/nbsp;2 f. 15." Ratio solutionis: Esto Tab. ג. in qua enumerantur 6 rerum abcdef com2nationes possibiles; prima autem res a ducta per caeteras facit com2nationes 5, nempe ipso numero unitate minores; secunda b per caeteras ducta tantum 4, non enim in antecedentem a duci potest, rediret enim prior com2binatio ba vel ab (haec enim in negotio combinationis nihil differrunt), ergo solum in sequentes quae sunt 4; similiter tertia c in sequentes ducta facit 3; quarta d facit 2; quinta e cum ultima f facit 1. Sunt igitur com2nationes 5. 4. 3. 2. 1. +. f. 15. Ita patet, numerum com2nationum componi ex terminis progressionis arithmeticae, cujus differentia l, numeratis ab l ad numerum numero rerum proximum inclusive, sive ex omnibus numeris Numero rerum minoribus simul additis. Sed quia, uti vulgo docent Arithmetici, tales numeri hoc compendio adduntur, ut maximus numerus ducatur in proxime majorem, facti dimidius sit quaesitus, et vero proxime major h. l. est ipse Numerus rerum, igitur perinde est ac si dicas, Numerum rerum ducendum in proxime minorem, facti dimidium fore quaesitum.
zur Übersetzung des Abschnitts
Probl. II.
Dato numero complexiones simpliciter inveniere.
Datus Numerus quaeratur inter Exponentes progressionis Geometricae duplae, numerus seu terminus progressionis ei e regione respondens demta Unitate erit quaesitum. Rationem, seu τό δίοτι difficile est vel concipere, vel si conceperis explicare: τό ὄτι tabula א manifestum est. Semper enim complexiones particulares simul additae, addita unitate, terminum·progressionis geometricae duplae constituent, cujus exponens sit numerus datus. Ratio tamen, siquis curiosius investiget, petenda erit ex discerptione in Practica Italica usitata, 𝔳𝔬𝔪 ℨ𝔢𝔯𝔣𝔞𝔢𝔩𝔩𝔢𝔫. Quae talis esse debet, ut datus terminus progressionis·geometricae discerpatur in una plures partes, quam sunt unitates exponentis sui, id est numeri rerum, quarum semper aequalis sit prima ultimae, secunda penultimae, tertia antepenultimae etc., donec vel, si in parem discerptus est numerum partium, exponente seu Numero rerum impari existente, in medio duae correspondeant partes per probl. 1 th. 5 (v. g. 128 de 7 discerpantur in partes 8 juxta tabulam א: l, 7, 21, 35, 21, 7, 1), vel si in imparem, exponente pari existente, in medio relinquatur unus nulli correspondens (v. g. 256 de 8 discerpantur in partes 9 juxta Tab. א: 1, 8, 28, 56, 70, 56, 28, 8, 1). Putet igitur aliquis, ex eo manifestum esse novum modum eumque absolutum solvendi probl. 1, seu dato exponente inveniendi Numerum complexionum, si nimirum ope Algebrae inveniatur discerptio Complexionum simpliciter seu termini progr. geom. duplae juxta modum datum; verum non sunt data sufficientia, et idem numerus in alias atque alias partes, eadem tamen forma, discerpi potest.
zur Übersetzung des Abschnitts
Usus Probl. I et II.
Cum omnia quae sunt aut cogitari possunt, fere componantur a partibus aut realibus aut saltem conceptualibus, necesse est, quae specie differunt aut eo differre, quod alias partes habent, et hic Complexionum usus, vel quod alio situ, hic Dispositionum, illic materiae, hic formae diversitate censentur. Imo Complexionum ope non solum species rerum, sed et attributa inveniuntur, ut ita tota propemodum Logicae pars inventiva illic circa terminos simplices, hic circa complexos fundetur in complexionibus, uno verbo et doctrina divisionum et doctrina propositionum. Ut taceam, quantopere partem logices Analyticam seu judicii diligenti de modis syllogisticis scrutatione exemplo 6. illustrare speremus.
In divisionibus triplex usus est complexionum: l. dato fundamento unius divisionis inveniendi species ejus; 2. datis pluribus divisionibus de eodem Genere, inveniendi species ex diversis divisionibus mixtas, quod tamen servabimus problemati 8.; 3. datis speciebus inveniendi genera subalterna. Exempla per totam philosophiam diffusa sunt, imo nec Jurisprudentiae deesse ostendemus, apud Medicos vero omnis varietas medicamentorum compositorum et φαρμακοποιητικἠ ex variorum ingredientium mixtione oritur, at in eligendis mixtionibus utilibus summo opus judicio est. Primum igitur exempla dabimus specierum hac ratione inveniendarum:
- apud JCtos l. 2. D. Mandati & pr. J. de Mandato haec divisio proponitur: Mandatum contrahitur 5. modiis: mandantis gratia, mandantis et mandatarii, tertii, mandantis et tertii, mandatarii et tertii. Sufficientiam divisionis hujus sic venabimur: Fundamentum ejus est finis ᾦ seu persona cujus gratia contrahitur, ea est triplex: mandans, mandatarius et tertius. Rerum autem trium complexiones sunt 7: Uniones tres: cum solius l. mandantis, 2. mandatarii, 3. tertii gratia contrahitur. Com2nationes totidem: 4. Mandantis & Mandatarii, 5. Mandantis & Tertii, 6. Mandatarii & Tertii gratia. Con3natio una, nempe 7. et mandantis et mandatarii et tertii simul gratia. Hic ICti Unionem illam, in qua contrahitur gratia mandatarii solum, rejiciunt velut inutilem, quia sit consilium potius quam mandatum; remanent igitur species 6, sed cur 5 reliquerint, omissa con3natione, nescio.
-
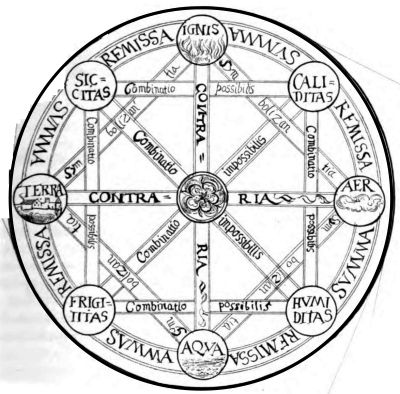 Elementorum numerum, seu corporis simplicis mutabilis species Aristoteles libr. 2. de Gen. cum Ocello Lucano Pythagorico deducit ex numero Qualitatum primarum, quas 4 esse supponit, tanquam fundamento, his tamen legibus, ut 1. quodlibet componatur ex duabus qualitatibus et neque pluribus neque paucioribus; hinc manifestum est Uniones, con3nationes et con4nationem esse abjiciendas, solas com2nationes retinendas, quae sunt 6. 2. ut nunquam in unam com2nationem veniant qualitates contrariae, hinc iterum duae com2nationes fiunt inutiles, quia inter primas has qualitates dantur duae contrarietates, igitur remanent com2nationes 4, qui est numerus Elementorum. Apposuimus Schema (vide paginam titulo tractatus proximam), quo origo Elementorum ex primis Qualitatibus luculenter demonstratur. Porro uti ex his illa Aristoteles, ita ex illis 4 temperamenta Galenus, horumque varias mixtiones medici posteriores elicuere, quibus omnibus jam superiori seculo se opposuit Claud. Campensius Animadvers. natural. in Arist. et Galen. adject. ad Com. ej. in Aph. Hippocr. ed. 8. Lugduni anno 1576.
Elementorum numerum, seu corporis simplicis mutabilis species Aristoteles libr. 2. de Gen. cum Ocello Lucano Pythagorico deducit ex numero Qualitatum primarum, quas 4 esse supponit, tanquam fundamento, his tamen legibus, ut 1. quodlibet componatur ex duabus qualitatibus et neque pluribus neque paucioribus; hinc manifestum est Uniones, con3nationes et con4nationem esse abjiciendas, solas com2nationes retinendas, quae sunt 6. 2. ut nunquam in unam com2nationem veniant qualitates contrariae, hinc iterum duae com2nationes fiunt inutiles, quia inter primas has qualitates dantur duae contrarietates, igitur remanent com2nationes 4, qui est numerus Elementorum. Apposuimus Schema (vide paginam titulo tractatus proximam), quo origo Elementorum ex primis Qualitatibus luculenter demonstratur. Porro uti ex his illa Aristoteles, ita ex illis 4 temperamenta Galenus, horumque varias mixtiones medici posteriores elicuere, quibus omnibus jam superiori seculo se opposuit Claud. Campensius Animadvers. natural. in Arist. et Galen. adject. ad Com. ej. in Aph. Hippocr. ed. 8. Lugduni anno 1576.
- Numerus communiter ab Arithmeticis distinguitur in Numerum stricte dictum ut 3. Fractum ut ⅔, Surdum ut Rad. 3. id est numerum qui in se ductus efficit 3, qualis in rerum natura non est, sed analogia intelligitur, & denominatum, quem alii vocant figuratum, v. g. quadratum, cubicum, pronicum. Ex horum commixtione efficit Hier. Cardanus Pract. Arith. c. 2. Species mixtas 11. Sunt igitur in universum complexiones 15, nempe uniones 4, quas diximus, Com2nationes 6: Numerus et Fractus, v. g. 3⁄2 aut 1 ½; Numerus et Surdus v. g. 7. ᴖ R. 3; Numerus et Denominatus v. g. 3 + cub. de A; Fractus et Denominatus v. g. ½ ᴖ cub. de A; Surdus et Denominatus v. g. cub. de 7; Con3nationes 4: Numerus et Fractus et Surdus, Numerus et Fractus et Denominatus, Numerus et Surdus et Denominatus, Fractus et Surdus et Denominatus; Con4natio l: Numerus et Fractus et Surdus et Denominatus. Loco vocis: Numerus, commodius substituetur vox: Integer. Jam 4. 6. 4. 1. + f. 15.
- Registrum, Germanice 𝔢𝔦𝔫 ℨ𝔲𝔤, dicitur in Organis Pneumaticis ansula quaedam, cujus apertura variatur sonus, non quidem in se melodiae aut elevationis intuitu, sed ratione canalis, ut modo tremebundus, modo sibilans etc. efficiatur. Talia recentiorum industria detecta sunt ultra 30. Sunto igitur in organo aliquo tantum 12 simplicia, ajo fore in universum quasi 4095; tot enim sunt 12 rerum Completiones simpliciter per tab. א, grandis organistis, dum modo plura, modo pauciora, modo haec, modo illa simul aperit, variandi materia.
- Th. Hobbes Element. de Corpore p. 1. c. 5 Res, quarum dantur termini in propositionem ingredientes, seu suo stylo, Nominata, quorum dantur nomina, dividit in Corpora (id est substantias, ipsi enim omnis substantia corpus) Accidentia, Phantasmata & Nomina, et sic nomina esse vel Corporum v. g. homo, vel Accidentium v.g. omnis abstracta, rationalitas, motus, vel Phantasmatum, quo refert spatium, tempus, omnes qualitates sensibiles etc., vel Nominum, quo refert secundas intentiones. Haec cum inter se sexies com2nentur, totidem oriuntur genera propositionum, et additis iis, ubi termini homogenei com2nantur (corpusque attribuitur corpori, accidens accidenti, phantasma phantasmati, notio secunda notioni secundae), nempe 4, exsurgunt l0. Ex iis solos terminos homogeneos utiliter combinari arbitratur Hobbes. Quod, si ita est, uti certe et communis philosophia profitetur, abstractum et concretum, accidens et substantiam, notionem primam et secundam male invicem praedicari, erit hoc utile ad artem inventivam propositionum, seu electionem com2nationum: utilium ex innumerabili rerum farragine, observare; de qua infra.
-
Venio ad exemplum complexionum haud paulo implicatius: determinationem numeri Modorum Syllogsmi Categorici. Qua in re novas rationes iniit Joh. Hospinianus Steinanus, Prof. Organi Basilecensis, vir contemplationum minime vulgarium libello paucis noto, edito in 8. Basileae an. 1560 hoc titulo: Non esse tantum 36 bonos malosque categorici syllogismi modos, ut Aristot. cum interpretibus docuisse videtur, sed 512. quorum quidem probentur 36, reliqui omnes rejiciantur.
zur Übersetzung des Abschnitts
Incidi postea in controversias dialecticas ejusdem, editas post obitum autoris Basileae 8. anno 1576, ubi quae in Erotematis Dialecticis libelloque de Modis singularia statuerat, velut quadam Apologia, ex 23 problematibus constante, tuetur; promittit ibi et libellum de inveniendi judicandique facultatibus, et Lectiones suas in universum Organon cum latina versione, quas ineditas arbitror fortasse ab autore conceptas potius, quam perfectas. Etsi autem variationem ordinis adhibere necesse est, quae spectat ad probl. 4, quia tamen potissimae partes complexionibus debentur, huc referemus. Cum libri hujus de Modis titulus primum se obtulit, antequam introspeximus, ex nostris traditis calculum subduximus hoc modo: Modus est dispositio seu forma syllogismi ratione quantitatis et qualitatis simul: Quantitate autem propositio est vel Universalis vel Particularis vel Indefinita vel Singularis; nos brevitatis causa utemur literis initialibus: U Universalis, P Particularis, I Indefinita, S Singularis; Qualitate vel Affirmativa vel Negativa, A Affirmativa, N Negativa. Sunt autem in Syllogismo tres propositiones, igitur ratione quantitatis Syllogismus vel est aequalis vel inaequalis: Aequalis, seu habens propositiones ejusdem quantitatis 4 modis: l) Syllogismus talis est: U, U, U. 2. P, P, P. 3. I, I, I. 4. S, S, S, ex quibus 19 sunt utiles: 2) 1mus et 4tus; inaequalis vel ex parte vel in totum: ex parte, quando duae quaecunque propositiones sunt ejusdem quantitatis, tertia diversae.
zur Übersetzung des Abschnitts
Et in tali casu duo genera quantitatis sunt in eodem Syllogismo, etsi unum bis repetitur: id toties diversimode contingit, quoties res 4 id est genera haec quantitatum U, P, ´J, S diversimode sunt com2nabilia nempe, 6𝔪𝔞𝔥𝔩, et in singulis 2 sunt casus, quia jam hoc bis repetitur, jam illud, altero simplici existente; ergo 6 ᴖ 2 f. 12. Atque ita rursus in singulis, ratione ordinis, sunt variationes 3, nam v. g. hoc U, U, P, vel ponitur uti jam, vel sic: P, U, U, vel sic: U, P, U; ergo 12 ᴖ 3 f. 36. Ex quibus utiles 18: 2 U(S) U(S) S(U), 2. U(S) S(U) U(S). 2. S(U) U(S) U(S). 4. U(S) U(S) P vel I: 4 UI (P)I (P) vel loco U, S, 4 I(P) I(P) et S loco U.
zur Übersetzung des Abschnitts
In totum inaequalis, quando nulla cum altera est ejusdem magnitudinis, et ita quemlibet Syllogismum ingrediuntur genera 3, toties alia quoties 4 res possunt con4nari, nempe 4𝔪𝔞𝔥𝔩. Tria autem ratione ordinis variantur 6𝔪𝔞𝔥𝔩, v. g. U, P, I; U, I, P; P, U, I; P, I, U; I, U, P; I, P, U. Ergo 4 ᴖ 6 f. 24. Ex quibus utiles 12. 2: UP(I)I(P), 2. I(P)UP(I); totidem si pro U ponas S. 4 + 4 f. 8. 2., U(S)S (U)P; totidem si pro P ponas I, 2 + 2 f. 4. Addamus jam: 4 + 36 + 24 f. 64. Hae sunt variationes Quantitatis solius. Ex quibus sunt utiles: 2 + 18 + 12 f. 32. Caeteri cadent per Reg. 1. ex puris particularibus nihil sequitur; 2. Conclusio nullam ex praemissis quantitate vincit; etsi fortasse interdum ab utraque vincatur, uti in Barbari.
zur Übersetzung des Abschnitts
Porro cum Qualitatis duae solam sint diversitates A et N, propositiones vero 3. Hinc repetitione opus est, et vel Modus est Similis, id est ejusdem qualitatis, vel dissimilis: hujus nulla ulterius est variatio, quia nunquam ex toto, sed semper ex parte est dissimilis, nunquam enim omnes propositiones sunt dissimiles, quia solum 2 sunt diversitates. Similis species sunt 2: A, A, A; N, N, N; dissimilis 2: A, A, N, vel N, N, A; dissimilis singulae variantur ratione ordinis 3𝔪𝔞𝔥𝔩, v. g. A, A, N; N, A, A; A, N, A. Ergo 2 ᴖ 3 f. 6+2 f. 8. Toties variatur Qualitas. Ex quibus utiles Variationes sunt 3: A A A; N A N; A N N, per reg. l, Ex puris negativis nihil sequitur; l) Conclusio sequitur partem in qualitate deteriorem. Sed quia modus est variatio Qualitatis et Quantitatis simul, et ita singulae variationes Quantitatis recipiunt singulas Qualitatis, hinc 64 ᴖ 8 f. 512.
zur Übersetzung des Abschnitts
Numerum omnium Modorum utilium et inutilium. Ex quibus utiles sic reperiris: duc variationes utiles quantitatis in qualitatis, 32 ᴖ 3 f. 96; de producto subtrahe omnes modos, qui continentur in Frisesmo, id est qui ratione Qualitatis quidem sunt A N N, ratione quantitatis vero Major prop. est I vel P, Minor autem U vel S, et conclusio I vel P, quales sunt 8. Frisesmo enim etsi modus est per se quodammodo subsistens, tamen est in nulla figura, v. infra, jam 96-8 f. 88. Numerum utilium Modorum Hospiniano, cui nostra methodus ignota, aliter, sed per ambages procedendum erat. Primum igitur cap. 2. 3. Aristotelicos modos 36 investigat ex complicatione U P I omisso S et conclusione; ex quibus utiles sunt 8: UA, UA in Barbara vel Daropti, UA, PA in Darii et Datisi, PA, UA in Disamis, UA, UN in Camestres, UN, UA in Celarent, Cesare, Felapton, UA, IN in Baroco, UN, IA in Ferio, Festino, Ferison, IN, UA in Bocardo. Quibus addit cap. 4. singulares similes aequales SA, SA, SN, SN, 2 inaequales 3ium generum singulis inversis, et quibuslibet vel A vel N eg. 3 ᴖ 2 ᴖ 2 f. 12+2 f. 14. Ex quibus Hospinianus solum admittit UA, PA, et ponit in Darii. Quia singulares ait particularibus aequipollere cum communi Logicorum schola, quod tamen mox falsum esse ostendemus. C. 5 addit singulares dissimiles totidem, nempe 14, ex quibus Hosp. solum admittit SN, UA in Bocardo; item UN, SA in Ferio. C. 6 addita conclusione quasi denuo incipiens enumerat modos similes aequales 4 ᴖ 2 f. 8, ex quibus utiles solum UA, UA, UA. in Barbara juxta Hospin. similes inaequales sunt vel ex toto inaequales, de quibus infra, vel ex parte, de quibus nunc, ubi duae propositiones sunt ejusdem quantitatis, tertia quaecunque diversae; et tunc modo duae sunt universales, una indefinita, quo casu sunt modi 6 (nam una vel initio vel medio vel fine ponitur 3, semperque aut omnes sunt A aut N. 3 ᴖ 2 fac. 6) vel contra etiam 6 per cap. 7. fac. 12. Ex solis prioribus 6 utilis est UA, IA, IA in Darii et Datisi; item IA, UA, IA in Disamis; item UA, UA, IA in Darapti, et, ut Hospinianus non inepte, in Barbari. Certe cum ex propositione UA sequantur duae PU, una conversa, hinc oritur modus indirectus Baralip; alterna subalterna l, v. g. Omne animal est substantia. Omnis homo est animal. E Quidam homo est substantia. Hinc oritur iste: Barbari. Totidem, nempe 12, sunt modi per caput 8, si duae U et una P jungantur, vel contra; et iidem sunt modi utiles, qui in proxima mixtione, si pro I substituas P. Totidem, nempe 12, sunt modi per c. 8, si jungantur duae U et una S per c. 9, et quia Hospin. habet S pro P, putat solum modum utilem esse in Darii UA, SA, SA; v. infra. Item 12 IIP vel PPI; omnes inutiles per c. l0. Item 12 IIS vel SSI, omnes, ut ille putatur, inutiles per c. 11. Item 12 PPS vel SSP, omnes, ut ille putatur, inutiles per c. 12. Jam 6 ᴖ 12 f. 72 + 8 fac. 80, numerum modorum similium additis variationibus Conclusionis. Dissimiles modi sunt vel aequales vel inaequales. Aequales sunt ex meris vel U vel P vel I vel S, 4 genera quae singula variantur ratione qualitatis sic: NNA, ANN etc. 6𝔪𝔞𝔥𝔩, uti supradiximus n. 20; jam 6 ᴖ 4 f. 24, v. cap. 13. utilis est: UA, UN, UN in Camestres.
zur Übersetzung des Abschnitts
Dissimiles inaequales sunt vel ex toto inaequales, ut nulla propositio alteri sit aequalis, de quibus infra, vel ex parte, ut duae sint aequales, una inaequalis, de quibus nunc. Et redeunt omnes variationes quantitatis, de quibus in similibus ex c. 7. 8. 9. l0. 11. 12. in singulis de binis contrariis diximus; modi autem hic fiunt plures quam illic, ob variationem qualitatis accedentem. Erat igitur in c. 7. UUI vel contra IIU. Ordo quantitatis variatur 3𝔪𝔞𝔥𝔩, quia v. g. I modo initio, modo medio, modo fine ponitur. Qualitatis tum complexus variatur 2𝔪𝔞𝔥𝔩, NNA vel AAN, tum ordo 3𝔪𝔞𝔥𝔩 uti supra dictum, ponendo A vel N initio aut medio aut fine, ergo 3 ᴖ 2 ᴖ 3 f. 18 de UUI, et contra etiam 18 de IIU f. 36, per c. 14. In prioribus 18 utiles sunt modi: UA, UN, IN; vel loco IN, PN aut SN, et sunt in modo Camestres, uti supra Barbari; UN, UA, I(P.S )N similiter in modo Celaro et Cesaro et Felapton; UA, I(P.S )N, I(P.S.)N in Baroco; UN, I(P.S.)A. I(P.S.)N in Ferio, Festino et Ferison, qui ultimus tamen in S locum non habet; I(P.S.)N, UA, I(P.S.)N in Bocardo. Similiter UUP vel PPU 36 modos habent. Utiles designavimus proxime per P in ( ). Similiter UUS vel SSU faciunt simul modos 36 per c. 15. Modos utiles proxime signavimus per S. IIP vel PPI faciunt similiter 36 per c. 16; modi omnes sunt inutiles. IIS et SSI et PPS et SSP faciunt modos 2 ᴖ 36 = 72 per c. 17, qui omnes sunt inutiles. Huc usque distulimus inaequales ex toto, ubi nulla propositio in eodem syllogismo est ejusdem quantitatis, sunt autem vel similes vel dissimiles; inaequales ex toto similes sunt: UIP, quae forma habet modos 12, nam 3 res variant ordinem 6𝔪𝔞𝔥𝔩, qualitas autem variatur 2𝔪𝔞𝔥𝔩; ergo 6 ᴖ 2 f. 12 per c. 18, ubi sunt inutiles: UA, I(PS)A, P(IS)A, UA, P(IS)A, I(PS)A in Darii et Datisi; I(P.S.)A, UA, P(I.S.)A, P(I.S.)A, UA, I(P.S.)A in Disamis, nisi quod S non ingreditur Minorem in Figura Tertia; UPS et UIS, quae Habent modos 24 per c. 10. Utiles signavimus proxime per S. IPS, quae habet modos 12 per c. 20; omnes autem sunt inutiles juxta Hosp.
zur Übersetzung des Abschnitts
Dissimiles omnino inaequales sunt eodem modo, uti similes: UIP quae variant ordinem 6𝔪𝔞𝔥𝔩 Qualitas autem variatur 6𝔪𝔞𝔥𝔩; ergo 6 ᴖ 6 f. 36 per c. 21. Modi utiles sunt: UA, I(P.S.)N, P(I.S.)N in Baroco; UN, I(P.S.)A, P(I.S.)N in Ferio, Festino et Ferison. I(P.S.)N, UA, P(I.S.)N in Bocardo. UIS et UPS, 36 ᴖ 2 f. 72 per c. 22. Modos utiles signavimus proxime per S et P et I in ( ). IPS habet modos 36 per c. 23, omnes inutiles juxta hypothesin Hosp. Addemus jam omnes modos a cap. 6 incl. ad c. 23 computatos (nam anteriores in his rediere) + 89. 24. 36. 36. 36. 36. 72. 12. 24. 12. 36. 72. 36. seu 80 + 12 ᴖ 36, f. 512. In his Hospiniani speculationibus quaedam laudamus, quaedam desideramus. Laudamus inventionem novorum modorum: Barbari, Camestres, Celaro, Cesaro; laudamus quod recte observavit, modos, qui vulgo nomen invenere, v. g. Darii; etc. habere se ad modos a se anumeratos velut genus ad speciem; sub Darii enim hi novem continentur ex ejus hypothesi: UA, IA, IA; UA, SA, SA; UA, PA, PA; UA, IA, SA; UA, SA, IA; UA, JA, PA; UA, PA, IA; UA, SA, PA; UA, PA, SA. Sed non aeque probare possumus, quod Singulares aequavit particularibus, quae res omnes ejus rationes conturbavit, effecitque ei modos utiles justo pauciores, ut mox apparebit. Hinc ipse in controversiis dialect. c. 22. p. 430 errasse se fatetur et admittit modos utiles 38. nempe 2 praeter priores 36. 1. in Darapti, cum ex meris UA concluditur SA, quoniam Christus ita concluserit Luc. XXIII. v. 37. 38; 2, in Felapton, cum ex UN et UA concluditur, SN quia ita concluserit Paulus Rom. IX. v. 13. Nos etsi scimus ita vulgo sentiri, arbitramur tamen alia omnia veriora. Nam haec: Socrates est Sophronisci filius, si resolvatur fere juxta modum Joh. Rauen, ita habebit: Quicunque est Socrates, est Sophronisci filius. Neque male dicitur: Omnis Socrates est Sophronisci filius, etsi unicus sit, (neque enim de nomine, sed de illo homine loquimur) perinde ac si dicam: Titio omnes vestes quas habeo, do lego, quis dubitet, etsi unicam habeam, ei deberi? Imo secundum ICtos universitas quandoque in uno subsistit I. municipium 7. D. quod cujusque univers. nom. Magnif. Carpzov. p. 11. c. VI. def. 17. Vox enim: omnis, non infert multitudinem, sed singulorum comprehensionem. Imo supposito quod Socrates non habuerit fratrem, etiam ita recte loquor: Omnis Sophronisci filius est Socrates. Quid de hac propositione dicemus: Hic homo est doctus? Ex qua recte concludemus: Petrus est hic homo, ergo Petrus est doctus. Vox autem: Hic, est signum singulare. Generaliter igitur pronunciare audemus: omnis Propositio singularis ratione modi in syllogismo habenda est pro universali, uti omnis indefinita pro particulari. Hinc etsi Modos utiles solum 36 numerat, sunt tamen 88, de quo supra, omissa nihilominus variatione, quae oritur ex figuris. Nam modi diversarum figurarum correspondentes, id est quantitate et qualitate convenientes, sunt unus simplex v. g. Darii et Datisi. Simplices autem modos voco, non computata figurarum varietate, Figuratos contra tales sunt modi figurarum, quos vulgo recensent. Age igitur, ne quid mancum sit, et ad hoc descendamus, dum servet impetus. Ad figuram requiruntur termini tres: Major, quem signabimus graece μ minor quem latine M; medium quem germanice 𝔐, et singuli bis. Ex his fiunt com2nationes 3, quae hic dicuntur propositiones, quarum ultima conclusio est, priores praemissae. Regulae com2nandi generales cuique figurae sunt: 1. nunquam com2nentur duo termini iidem, nulla enim propositio est: MM seu minor minor. 2. M et 𝔐 solum com2nentur in Conclusione, ita ut semper praeponatur M hoc modo: M𝔐. 3) in praemissarum 1ma com2nentur 𝔐 et M, in secunda M et μ. Neque enim pro variatione figurae habeo, quando aliqui praemissas transponunt, et loco hujus: B est C, A est B, ergo A est C, ponunt sic: A est B, B est C, ergo A est C, uti collocant P. Ramus, P. Gassendus, nescio quis I. C. E. libello peculiari edito, et jam olim Alcinous lib. l. Doct. Plat. qui semper Majorem prop. postponunt, Minorem prop. praeponunt. Sed id non variat figuram, alioqui tot essent figurae, quot variationes numerant Rhetores, dum in vita communi conclusionem nunc initio, nunc medio, nunc fine quam observant.
zur Übersetzung des Abschnitts
Manifestum igitur, figurarum varietatem oriri ex ordine medii in praemissis, dum modo in majore praeponitur, in minore postponitur, quae est Aristotelica I. modo in majore et minore postponitur, quae est Arist II. modo utrobique praeponitur, quae est III. modo in Majore postponitur, in Minore praeponitur quae est IV Galeni (frustra ab Hospiniano contr. Dial. Probl. 19. tributa Scoto, cum ejus meminerit Aben Rois) quam approbat Th. Hobbes Elem. de Corp. P. l c. 4. art. 11. Designabuntur sic: I. 𝔐μ· M𝔐, Mμ, II. μM, M𝔐, Mμ III. 𝔐μ, 𝔐M, Mμ. IV. μ𝔐, 𝔐M, Mμ. 1Vtae figurae hostibus unum hoc interim oppono: Quarta figura aeque bona est ac ipsa prima; imo si modo, non praedicationis, ut vulgo solent, sed subjectionis, ut Aristoteles, eam enunciemus, ex IV fiet I, et contra. Nam Arist. ita solet hanc v. g. propositionem: omne α est β, enunciare: β inest omini α. IVtae igitur figurae designatio orietur talis: 𝔐 inest τῷ μ, M, inest τῷ 𝔐, ergo M est μ; vel ut conclusio etiam sic enuncietur, transponendae praemissae, et conclusio erit: Ergo μ inest τῷ M. Idem in aliis fieri figuris potest, quod reducendi artificium nemo observavit hactenus.
zur Übersetzung des Abschnitts
Caeterum secunda oritur ex prima, transposita propositione majore; 3tia, transposita minore; 4ta, transposita conclusione, sed hic alius efficitur syllogismus, quia alia conclusio. Unde modi hujus 4tae sunt designandi modis indirectis primae figurae ut vulgo vocant, dummodo praeponas majorem propositionem minori, non contra, ut vulgo contra morem omnium figurarum hanc unicam ob causam, ut vitaretur quarta Galeni, factum est, v. g. sit Syllogismus in Baralip: Omne animal est substantia, omnis homo est animal, ergo quaedam substantia est homo. Certe substantia est minor terminus, igitur praemissa in qua ponitur, est minor, et per consequens propositio haec: Omne animal est substantia, non est ponenda primo secundo loco, tum prodibit ipsissima IVta figura.
zur Übersetzung des Abschnitts
Propter hanc transpositionem propositionum, quos vulgo Syllogismos in Celantes ponunt, sunt in Fapesmo, loco Frisesmo dicendum Fresismo, loco Dabitis Ditabis; Baralip manet. Hi sunt modi figurae IVtae, quibus addo Celanto et Colanto. Erunt simul 6 Modi: 1mae sunt 6: Barbara, Celarent, Darii, Ferio, Barbari, Celaro; Modi IIIdae 6: Cesare, Camestres, Festino, Baroco, Cesaro, Camestres. Modi IIItiae etiam 6: Darapti, Felapton, Disamis, Datisi, Bocardo, Ferison. Ita ignota hactenus figurarum harmonia detegitur, singulae enim modis sunt aequales; l) Imae autem et 2dae figurae semper Major propositio est U; 2) Imae et IIItiae semper Minor A; 3) in IIda semper conclusio N; 4) in IIItia Conclusio semper est P; in IVta conclusio nunquam est UA, Major nunquam PN, etsi minor N, major UA. Propter has regulas fit, ut non quilibet 88 modorum utilium in qualibet figura habeat locum; alioqui essent Modi utiles: 4 ᴖ 96 f. 348. Modi autem figurati in universum utiles et inutiles 512 ᴖ 4 f. 2048. Qui autem in qua figura sint utiles, praesens schema docebit:
zur Übersetzung des Abschnitts
0 4 3 2 1 8 UA, UA, UA. SA, SA, SA. UA, UA, SA. UA, SA, UA. SA, UA, UA. SA, SA, UA. SA, UA, SA. GA. SA, SA. 1 … — — — Barbara. 8 UN, UA, UN. SN, SA, SN. UN, UA, SN. UN, SA, UN. SN, UA, UN. SN, SA, UN. SN, UA, SN. UN, SA, SN. 2 … — — Cesare. Celarent. 8 UA, UN, UN. SA, SN, SN. UA, UN, SN. UA, SN, UN. SA, UN, UN. SA, SN, UN. SA, UN, SN. UA, SN, SN. 3 … — — Camestres. — 8 UA, UA, PA. UA, UA, IA. SA, SA, PA. SA, SA, IA. UA, SA, IA. UA, SA, PA. SA, UA, IA. SA, UA, PA. 4 … Baralip. Darapti. — Barbari 8 UN, UA, PN. UN, UA, IN. SN, SA, PN. SN, SA, IN. UN, SA, IN. UN, SA, PN. SN, UA, IA. SN, UA, PN. 5 … Celanto. Felapt. Cesare. Celaro. 8 UA, UN, PN. UA, UN, IN. SA, SN, PN. SA, SN, IN. UA, SN, IN. UA, SN, PN. SA, UN, IN. SA, UN, PN. 6 … Fapesmo. — Camestres. — 8 UA, IA, IA. UA. PA, PA. UA, PA, IA. UA, IA, PA. SA, IA, IA. SA, PA, PA. SA, PA, IA. SA, IA, PA. 7 … — Datisi. — Darii. 8 UN, IA, IN. UN, PA, PN. UN, PA, IN. UN, IA, PN. SN, IA, IN. SA, PA, PN. SN, PA, IN. SN, IA, PN. 8 … Fresismo. Ferison. Festino. Ferio. 8 UA, IN, IN. UA, PN, PN. UA, PN, IN. UA, IN, PN. SA, IN, IN. SA, PN, PN. SA, PN, IN. SA, IN, PN. 9 … — — Baroco. — 8 IA, UA, IA. PA, UA, PA. IA, UA, PA. PA, PA, UA. IA, SA, IA. PA, SA, PA. IA, SA, PA. PA, SA, IA. 10 … Ditabis. Disamis. — — 8 IN, UA, IN. PN, UA, PN. IN, UA, PN. PN, PA, UN. IN, SA, IN. PN, SA, PN. IN, SA, PN. PN, SA, IN. 11 … Colanto. Bocardo. — — Restat. 8 IA, UN, IN. PA, UN, PN. IA, UN, PN. PA, UN, IN. IA, SN, IN. PA, SN, PN. IA, SN, PN. PA, SN, IN. 12 Frisesmo. — — — — In quo descripti sunt omnes modi utiles, ex quibus octo semper constituunt modum figuratum generalem, tales autem voco illos vulgo appellatos, in quibus U et S, item I et P habentur pro iisdem. Ipsae lineae modorum constant ex quatuor trigis, in qualibet lineae quantitate conveniunt, differunt pro tribus illis utilibus qualitatis differentiis. Ipsae autem trigae inter se differunt quantitate, positae eo ordine quo supra variationes ejus invenimus, in quarum quatuor reducuntur omnes supra inventae, quia hic U et S, item I et P reducuntur ad eandem. Cuilibet lineae ad marginem posuimus modos figuratos generales, in quos quilibet ejus modus specialis cadit. In summo signavimus numeris figuram.
zur Übersetzung des Abschnitts
Ex eodem autem manifestum est, modos figuratos generales esse vel Monadicos, vel correspondentes, et hos vel 2 vel 3 vel 4, prout plures paucieresve uni lineas sunt oppositi. Singulas porro lineae habent unum modum simplicem generalem, quem explicare possumus sumtis vocalibus, uti vulgo, ut A sit UA (vel SA), E sit UN (vel SN), I sit P {vel I) A, O sit P(I)N (ita omittendae sunt 4 praeterea vocales U pro IA; Y pro IN ; OY seu ον pro SA; ω pro SN; quas ad declarandum Hospinianum posuit Joh. Regius, quem vid. Disp. Log. lib. 4 probl 5), et ita modus lineae l. est AAA, 2. EAE, 3. AEE, 4. AAI, 5. EAO, 6. AEO, 7. AII, 8. EIO, 9. AOO, 10. IAI, 11. AEE, 12. IEO, abjectis nempe consonantibus ex vocibus vulgaribus, in quibus Scholastici per consonas figuram, per vocales modos simplices designarunt. Ultimus vero modus: IEO, quam diximus Frisesmo, et collocavimus in figura nulla, propterea est inutilis, quia major est P (hinc locum non habet in 1 et 2), minor vero N (hinc locum non habet in l et 3), etsi ex regulis modorum non sit inutilis. Quod vero in 4 locum non habeat, exemplo ostendo: Quoddam Ens est homo, Nullus homo est Brutam, E. Quoddam brutum non est Ens.
zur Übersetzung des Abschnitts
Atque hic obiter consilium suppeditabo utile, quod vel ipso exemplo hoc comprobatur, in quo consistit proba, ut sic dicam, seu ars examinandi modum propositum, et sicubi non formae, sed materiae vi concludit, celeriter instantiam reperiendi, qualem apud Logicos hactenus legere me non memini. Breviter: Pro UA sumatur propositio, quam materia non patitur converti simpliciter, v. g. sumatur haec potius: Omnis homo est animal, quam: Omnis homo est animal rationale, et quo remotius genus sumitur, hoc habebis accuratius. Pro UN eligatur talis, qua negentur de se invicem species quam maxime invicem vicinae sub eodem genere proximo, v. g. homo est brutum, et quae non sit convertibilis per contrapositionem in UA seu cujus neque subjectum neque praedicatum sit terminus infinitus. Pro P(I)A sumatur semper talis, quae non sit subalterna alicujus UA, sed in qua de genere quam maxime generali dicatur species particulariter. Pro (I)PN sumatur, quae non sit subalterna alicujus UN, et cujus neuter terminus sit infinitus, et in qua negetur de genere maxime remoto species.
zur Übersetzung des Abschnitts
Quod diximus de terminis infinitis vitandis, ejus ratio nunc patebit. Prodiit cujusdam Joh. Christoph. Sturmii Compendium Universalium seu Metaphysicae Euclideae ed. 8. Hagae anno 1660 apud Adrian. Vlacq. Cui annexuit novos quosdam modos syllogisticos a se demonstratos, qui omnes videntur juxta communem sententiam inpingere in alteram vel utramque harum duarum regularum qualitatis: Ex puris negativis nihil sequitur; et: Conclusio sequitur qualitatem debilioris ex praemissis. Ut tamen recte procedat argumentum, vel assumit propositionem affirmativam infiniti subjecti, quae stet pro negativa finiti, aut contra, v. g. aequipollent; Quidam non lapis est homo, et: quidam lapis non est homo (verum annoto, non procedere in universali contra, v. g. omnis lapis non est homo, ergo omnis non lapis est homo); vel assumat negativam infiniti praedicati pro affirmativa finiti vel contra, v. g. aequipollent: omnis philosophus non est non homo, et: est homo; vel 3 assumat loco datae conversam ejus per contrapositionem. Jam UA convertitur per contrap. in UN, U et PN in PA, ita facile illi est elicere ex puris neg. affirmantem, si negativae ejus tales sunt, ut stent pro affirmativis; item ex A et N elicere affirmantem, si ista stet pro negativa. Ita patet, omnes illas 8 variationes qualitatis fore utiles, et per consequens modos utiles fore 32 ᴖ 8 f. 256 juxta nostrum calculum. Similis fere ratio est syllogismi ejus, de quo Logici disputant: Quicumque non credunt, damnantur, Judaei non credunt, ergo damnantur. Sed ejus expeditissima solutio est, minorem esse affirmantem, quia medius terminus affirmatur de minore. Medius terminus autem non est: credere, sed: non credere, id enim praeexstitit in majori prop. Non possum hic praeterire modum Darapti ex ingenioso invento Cl. Thomasii nostri. Is observavit ex Ramo Schol. Dialect. lib. 7. c. 6. pag. m. 214, Conversionem posse demonstrari per syllogismum adjiciendo propositionem identicam, v. g. UA in PA sic: omne α est γ, omne α est α (si in 3tiae modo Darapti velis, vel omne γ est γ, si in 4tae modo Baralip), ergo quoddam γ est α. Item PA in PA sic: Quoddam α est γ. omne α est α (si in 3tiae modo Disamis velis, vel omne γ est γ. si in 4tae modo Ditabis), ergo quoddam γ est α. Item UN in UN (in Cesare 2dae) sic: Nullum α est γ, omne γ est γ, ergo nullum γ est α. Item PN vel in Baroco 3tiae sic : omne α est α, quoddam α non est γ, ergo quoddam γ non est α (vel in Colanto 4tae: Quoddam α non est γ, omne γ est γ, ergo quoddam γ non est α). Idem igitur ipse in Conversione per Contrapositionem tentavit, v. g. hujus PN: Quidam homo non est doctus, in hanc PA infiniti subjecti: quoddam non doctum est homo. Syllogismus in Darapti erit talis: Omnis homo est homo, quidam homo non est doctus, ergo quoddam quod non est doctum est homo. Observari tamen hic duo debent, Minorem juxta Sturmianam doctrinam videri quasi pro alia positam: Quidam homo est non doctus; deinde omnium optime sic dici: propositionis hujus: Quidam homo non est doctus, conversam per contrapositionem proprie hanc esse etiam negativam: Quoddam doctum non est non non homo, et in conversione per contrapositione identicam ipsam debere esse contrapositam, id ostendit syllogismus jam non amplius in Darapti, sed Baroco: Omnis homo est non non homo (id est, omnis homo est homo), quidam homo non est doctus, ergo quoddam doctum non est non non homo (id est, quoddam non doctum est homo).
zur Übersetzung des Abschnitts
Caeterum Sturmianos illos modos arbitror non formae, sed materiae ratione concludere, quia quod termini vel finiti vel infiniti sint, non ad formam propositionis seu copulam aut signum pertinet, sed ad terminos. Desinemus tandem aliquando modorum, nam etsi minime pervulgata attulisse speramus, habet tamen et novitas taedium in per se taediosis. Ab instituto autem abiisse nemo non dicet, qui omnia ex intima variationum doctrina erui viderit, quae sola prope per omne infinitum obsequentem sibi ducit animum, et harmoniam mundi et intimas constructiones rerum seriemque formarum una complectitur, cujus incredibilis utilitas perfecta demum philosophia, aut prope perfecta recte aestimabitur.
-
Nam VIImus est in complicandis figuris geometricis usus, qua in re glaciem fregit Joh. Keplerus lib. 2. Harmonicῶν. Istis complicationibus non solum infinitis novis theorematibus locupletari geometria potest, nova enim complicatio novam figuram compositam efficit, cujus jam contemplando proprietates, nova theoremata, novas demonstrationes fabricamus, sed et (si quidem verum est, grandia ex parvis, sive haec atomos sive moleculas voces, componi) unica ista via est in arcana naturae penetrandi, quando eo quisque perfectius rem cognoscere dicitur, quo magis rei partes et partium partes, earumque figuras positusque percepit. Haec figurarum ratio primum abstracte in geometria ac stereometria pervestiganda: inde ubi ad historiam naturalem existentiamque, seu id quod revera invenitur in corporibus, accesseris, patebit Physicae porta ingens, et elementorum facies, et qualitatum origo et mixtura, et mixturae origo et mixtura mixturarum, et quicquid hactenus in natura stupebamus.
zur Übersetzung des Abschnitts
Caeterum brevem gustum dabimus, quo magis intelligamur: Figura omnis simplex aut rectilinea aut curvilinea est. Rectilineae omnes symmetrae, commune enim omnium principium: Triangulus. Ex cujus variis complicationibus congruis omnes Figurae rectilineae coeuntes (id est non hiantes) oriuntur. Verum curvilinearum neque circulus in ovalem etc. neque contra reduci potest, neque ad aliquid commune. Neutra vero triangulo et triangulatis symmetros. Porro quilibet circulus cuicunque circulo est symmetros, nam quilibet cuilibet aut concentricus est aut esse intelligitur; Ovalis vero vel Elliptica ea tantum symmetros quae concentrica intelligitur; ita neque omnis ovalis ovali symmetros est etc. Haec de simplicibus; jam ad complicationes. Complicatio est aut congrua aut hians: congrua tum, cum figurae compositae lineae extremae seu circumferentiales nunquam faciunt angulum extrorsum, sed semper introrsum. Extrorsum autem fit angulus, cum portio circuli inter lineas angulum facientes descripta ex puncto concursus tanquam centro, cadit extra figuram, ad cujus circumferentiam lineae angulum facientes pertinent: introrsum, cum intra. Hians est complicatio, cum aliquis angulus fit extrorsum. Stella autem est complicatio hians, cujus omnes radii (id est lineae stellae circumferentiales angulum·extrorsum facientes) sunt aequales, ita ut si circulo inscribatur, ubique eum radiis tangat. Caeterum hiantes figurarum complicationes texturas voco, congruas proprie figuras. Sunt tamen et quaedam Texturae figuratae, quas et figurae hiantes ad oppositionem coeuntium voco.
zur Übersetzung des Abschnitts
Jam sunt theoremata: l) Si duae figurae asymmetrae sunt contiguae (complicatio enim vel immediata est contiguitas, vel mediata, inter tertium et primum, quoties tertium contiguum est secundo, et secundum vel mediate vel immediate primo), complicatio fit hians. 2) Curvilinearum inter se omnis contiguitas est hians, nisi alteri circumdetur Zona alterius symmetri dato concentrici. 3) Curvilineae cum rectilinea omnis contiguitas est hians, nisi in medio Zonae ponatur rectilinea. Zonam autem voco residuum in figura curvilineae majori, exempta concentrica minori. In contiguitate rectiliaearum autem aut angulus angulo, aut angulus lineae, aut linea lineae imponitur. 4) Si angulus angulo imponitur aut lineae, contiguitas est in puncto. 5) Omnis curvilinearum inter se contiguitas hians est in puncto. 6) Omnis earum cum rectis contiguitas etiam non hians, itidem. 7) Linea lineae nonnisi ejusdem generis imponi potest, v. g. recta rectae, curvilinea ejusdem generis et sectionis. 8) Si linea lineae aequali imponatur, contiguitas est congrua, si inaequali, hians.
zur Übersetzung des Abschnitts
Observandum autem est plures figuras ad unum punctum suis angulis componi posse, quae est textura omnium maxime hians. Sed et hoc fieri potest, ut duae vel plures contiguae sint hiantes, accedat vero tertia vel plures, et efficiatur una figura, seu complicatio congrua. Unde nova contemplatio oritur, quae figura vel textura quibus addita faciat ex textura figuram, quod nosse magni momenti est ad rerum hiatus explendos. Restat ut computationem ex nostris praeceptis instituamus, ad quam requiritur ut determinetur numerus figurarum ad conficiendam texturam, et determinentur figurae complicandae; utrumque enim alias infinitum est. Sed hoc facile cuilibet juxta enumeratos casus et theoremata praestare; nobis ad alia properantibus satis est prima lineamenta duxisse tractationis de Texturis hactenus fere neglectae. Decebat fortasse doctrinam hanc illustrare schematibus, sed intelligentes non indigebunt; imperiti, uti fieri solet, nec intelligere tanti aestimabunt.
-
VIIIvus Usus est in casibus apud Jureconsultos formandis. Neque enim semper exspectandum est praecipue legislatori, dum casus emergat; et majoris est prudentiae leges quam maxime initio sine vitiis ponere, quam restrictionem ac correctionem fortunae committere. Ut taceam, rem judicariam in qualibet republica hoc constitutam esse melius, quo minus est in arbitrio judicis. Plato lib. 9. de Leg. Arist. I. Rhet. Menoch. Arbitr. Jud. lib. 1. prooem. n. 1.
zur Übersetzung des Abschnitts
Porro Ars casuum formandorum fundatur in doctrina nostra de Complexionibus. Jurisprudentia enim cum in aliis geometriae similis est, tum in hoc quod utraque habet Elementa, utraque casus. Elementa sunt simplicia, in geometria figurae: triangulus, circulus etc. in Jurisprudentia: actus, promissum, alienatio etc. Casus: complexiones horum, qui utrobique variabiles sunt infinities. Elementa Geometriae composuit Euclides, Elementa juris in ejus Corpore continentur, utrobique tamen admiscentur Casus insigniores. Terminos autem in jure simplices, quorum mixtione caeteri oriuntur, et quasi Locos communes, summaque genera colligere instituit Bernhardus Lavinheta, Monachus ordinis Minorum, Com. in Lullii Artem magnam, quem vide.
zur Übersetzung des Abschnitts
Nobis sic visum: Termini quorum complicatione oritur in Jure diversitas casuum, sunt: Personae, Res, Actus, Jura. Personarum genera sunt tum naturalia, ut: mas, foemina, hermaphroditus, monstrum, surdus, mutus, caecus, aeger, embryo, puer, juvenis, adolescens, vir, senex, atque aliae differentiae ex physicis petendae, quae in jure effectum habent specialem; tum artificialia, nimirum genera vitae, corpora seu collegia et similia. Nomina officiorum huc non pertinent, quia complicantur ex potestate et obligatione; sed ad jura.
zur Übersetzung des Abschnitts
RES sunt mobiles, immobiles, dividuae (homogeneae), individuae, corporales, incorporales, et speciatim: Homo, animal cicur, ferum, rabiosum, noxium; Equus, aqua, fundus, mare etc., et omnes omnino res, de quibus peculiare est jus. Hae differentiae petendae ex physicis.
zur Übersetzung des Abschnitts
ACTUS (at non actus seu status) considerandi qua naturales: ita dividui, individui, relinquunt άποτέλεσμα vel sunt facti transeuntis; detentio quae est materiale possessionis, traditio, effractio, vis, caedes, vulnus; noxa, huc temporis et loci circumstantia, hae differentiae itidem petendae ex physicis; qua morales: ita sunt actus spontanei, coacti, necessarii, mixti, significantes, non significantes; inter significantes verba, consilia, mandata, praecepta, pollicitationes, acceptationes, conditiones. Haec omnis verborum varietas et interpretatio ex Grammaticis. Denique actus sunt vel juris effectum habentes, vel non habentes, et illi quidem pertinent ad catalogum jurium quae efficiunt, hi ex politicis ethicisque uberius enumerandi.
zur Übersetzung des Abschnitts
JURIUM itidem enumerandae vel species rei differentiae. Et hae quidem sunt v. g. realia, personalia; pura, dilata, suspensa; mobilia vel personae aut rei affixa etc. Species v. g. dominium, directum, utile; servitus, realis, personalis; aut ususfructus, usus, proprietas, jus possidendi, usucapiendi conditio; Potestas, obligatio (active sumta); Potestas administratoria, rectoria, coercitoria. Tum actus judiciales sumti pro jure id agendi tales sunt: postulatio, seu jus exponendi desiderium in judicio, cujus species pro ratione ordinis: actio, exceptio, replica etc. nempe in termino; tum in scriptis aut alias extra terminum; supplicatio pro impetranda citatione pro monitorio etc. Jurium autem catalogus ex sola Jurisprudentia sumitur.
zur Übersetzung des Abschnitts
Nos hic festini quicquid in mentem venit attulimus, saltem ut mens nostra perspiceretur; alii termini simplices privata cujusque industria suppleri possunt. Sed ita ut eos tantum ponat terminos, qui revera sunt simplices, id est quorum conceptus ex aliis homogeneis non componitur, quanquam in locis communibus, quorum disponendorum artificium potissimum huc redit, licebit terminos complexos simplicibus valde vicinos etiam tamquam peculiarem titulum collocare, v. g. compensationem, quae componitur ex obligatione Titii Cajo, et ejusdem Caji Titio in rem dividuam, homogeneam seu commensurabilem, quae utraque dissolvitur in summam concurrentem.
zur Übersetzung des Abschnitts
Ex horum terminorum simplicium, tum cum se ipsis aliquoties repetitis, tum cum aliis com2natione, con3natione etc. et in eadem complexione, variatione situs prodire casus prope infinitos quis non videt? Imo qui accuratius haec scrutabitur, inveniet regulas eruendi casus singulariores etc., nos talia quaedam concepimus, sed adhuc impolitiora, quam ut afferre audeamus.
zur Übersetzung des Abschnitts
Par in Theologia terminorum ratio est, quae est quasi Jurisprudentia quaedam specialis, sed eadem fundamentalis ratione caeterarum. Est enim velut doctrina quaedam de Jure publico, quod obtinet in Republica DEI in homines, ubi Infideles quasi rebelles sunt, Ecclesia velut subditi boni, personae Ecclesiasticae, imo et Magistratus Politicus velut Magistratus subordinati, Excommunicatio velut Bannus, Doctrina de Scriptura sacra et verbo DEI velut de legibus et earum interpretatione; de Canone, quae leges authenticae, de Erroribus fundamentalibus quasi de delictis capitalibus, de Judicio extremo et novissima die velut de Processu Judiciario et Termino praestituto, de Remissione Peccatorum velut de jure aggratiandi, de Damnatione aeterna velut de poena capitali etc.
-
Hactenus de usu complexionum in speciebus divisionum inveniendis; sequitur IXmus usus: Datis speciebus divisionis, praedivisiones seu genera et species subalternas inveniendi. Ac siquidem divisio, cujus species datae sunt, est διχοτομία, locum problema non habet, neque enim ea est ulterius reducibilis; sin πολυτομία omnino.
zur Übersetzung des Abschnitts
Esto enim τριχοτομία inter πολυτομίας minima, seu dati generis species 3: a, b, c; con3natio igitur earum tantum 1. est in dato genere summo; Uniones vero 3; illic ipsum prodit genus summum, hic ipsae species infimae, inter con3nationem autem et Unionem sola restat com2natio. Trium autem rerum com2nationes sunt 3, hinc oriuntur 3 genera intermedia, nempe abstractum seu genus proximum τῶν a. b., item τῶν b. c., item τῶν a. c. Ad genus autem requiritur tum ut singulis competat, tum ut cum omnibus disjunctive sumtis sit convertibile.
zur Übersetzung des Abschnitts
Exemplo res fiet illustrior. Genus datum sit respublica, species erunt 3, loco A Monarchia, loco B Oligarchia Polyarchica seu optimatum, loco C Panarchia; bis enim terminis utemur commodissime, ut apparebit, et voce Panarchiae etsi alio sensu, usus est Fr. Patritius Tomo inter sua opera peculiari ita inscripto, quo Hierarchias coelestes explicuit. Polyarchiae voce tanquam communi oligarchiae et panarchiae usus est Boxhornius lib. 2. c. 5. Inst. Polit. igitur 1) Genus subalternum τῶν AB seu Monarchiae et regiminis Optimatum erit Oligarchia.
zur Übersetzung des Abschnitts
Imperant enim vel non omnes: Oligarchia, sed vel unus: Monarchia, vel plures: Oligarchia, Polyarchia; vel omnes: Panarchia. 2) Genus subalternum τῶν B C erit Polyarchia; imperat enim vel unus: Monarchia, vel plures: Polyarchia (in qua iterum vel non omnes: Polyarchia, Oligarchia, vel omnes: Panarchia). 3) Genus subalternum τῶν A C est Respublica extrema. Nam species reipublicae alia intermedia est optimatum (hinc et nomen duplex: Oligarchia polyarchica), alia Extrema. Extremae autem sunt in quibus imperat unus, item in quibus omnes.
zur Übersetzung des Abschnitts
Ita in minima τῶν πολυτομίων, τριχοτομία, usum complexionum manifestum fecimus, quantae, amabo, in divisione virtutum in 11 species, similibusque aliis erunt varietates? ubi non solum singulae com2nationes, sed et con3nationes etc. usque ad con10nationes, eruntque computato genere summo et speciebus infirmis in universum complicationes seu genera speciesque possibiles 2047.
zur Übersetzung des Abschnitts
Nam profecto tam est in abstrahendo foecundus animus noster, ut datis quotcunque rebus, genus earum, id est conceptum singulis communem et extra ipsas nulli, invenire possit. Imo etsi non inveniat, sciet Deus, invenient angeli; igitur praeexistet omnium ejusmodi abstractionum fundamentum.
zur Übersetzung des Abschnitts
Haec tanta varietas generum subalternorum facit, ut in praedivisionibus seu tabellis construendis, invenienda etiam datae alicujus in species infimas divisionis sufficientia diversas vias ineant autores, et omnes nihilominus ad easdem infimas species perveniant. Deprehendet hoc, qui consulet Scholasticos numerum praedicamentorum, virtutum cardinalium, virtutum ab Aristotele enumeratarum, affectuum etc. investigantes.
-
A divisionibus ad propositiones tempus est ut veniamus, alteram partem Logicae inventionis. Propositio componitur ex subjecto et praedicato, omnes igitur propositiones sunt com2nationes. Logicae igitur inventivae propositionum est hoc problema solvere: 1) dato subjecto praedicata; 2) dato praedicato subjecta invenire, utraque tum affirmative, tum negative.
zur Übersetzung des Abschnitts
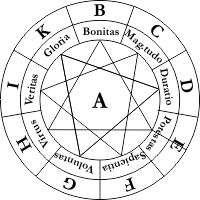 Vidit hoc Raym. Lullius Kabbalae Tr. 1. c. fig. 1. p. 46, et ubi priora repetit pag. 239 Artis magnae. Is, ut ostendat, quot propositiones ex novem illis suis terminis universalissimis: Bonitas, magnitudo, duratio etc. quas singulas de singulis praedicari posse dicit, oriantur, describit circulum, ei inscribit ἐννεάγωνον figuram regularem, cuilibet angulo ascribit terminum, et a quolibet angulo ad quemlibet ducit lineam rectam. Tales lineae sunt 36, tot nempe quot com2nationes 11 rerum. Cumque variari situs in qualibet com2natione possit bis, seu propositio quaelibet converti simpliciter, prodibit 36 ᴖ 2 f. 72, qui est numerus propositionum Lullianarum. Imo talibus complexionibus omne artificium Lullii absolvitur, vide ejusdem operum Argentorati in 8. anno 1698 editorum pag. 49. 53. 68. 135, quae repetuntur p. 240. 244. 245. Idem tabulam construxit ex 84 columnis constantem, quarum singulae continent 20 complexiones, quibus enumerat con4nationes suarum regularum literis alphabeticis denominatarum; ea tabula occupat pag. 260. 261. 262. 263. 264. 265. 266. Con3nationum vero tabulam habes apud Henr. Corn. Agrippam Com. in artem brevem Lullii, quae occupat 9 paginas, a pag. 863 usque 87l inclusive. Eadem ex Lullio pleraque exequitur, sed brevius Joh. Heinr. Alstedius in Architectura Artis Lullianae, inserta Thesauro ejus Artis Memorativae pag. 47 et seqq.
Vidit hoc Raym. Lullius Kabbalae Tr. 1. c. fig. 1. p. 46, et ubi priora repetit pag. 239 Artis magnae. Is, ut ostendat, quot propositiones ex novem illis suis terminis universalissimis: Bonitas, magnitudo, duratio etc. quas singulas de singulis praedicari posse dicit, oriantur, describit circulum, ei inscribit ἐννεάγωνον figuram regularem, cuilibet angulo ascribit terminum, et a quolibet angulo ad quemlibet ducit lineam rectam. Tales lineae sunt 36, tot nempe quot com2nationes 11 rerum. Cumque variari situs in qualibet com2natione possit bis, seu propositio quaelibet converti simpliciter, prodibit 36 ᴖ 2 f. 72, qui est numerus propositionum Lullianarum. Imo talibus complexionibus omne artificium Lullii absolvitur, vide ejusdem operum Argentorati in 8. anno 1698 editorum pag. 49. 53. 68. 135, quae repetuntur p. 240. 244. 245. Idem tabulam construxit ex 84 columnis constantem, quarum singulae continent 20 complexiones, quibus enumerat con4nationes suarum regularum literis alphabeticis denominatarum; ea tabula occupat pag. 260. 261. 262. 263. 264. 265. 266. Con3nationum vero tabulam habes apud Henr. Corn. Agrippam Com. in artem brevem Lullii, quae occupat 9 paginas, a pag. 863 usque 87l inclusive. Eadem ex Lullio pleraque exequitur, sed brevius Joh. Heinr. Alstedius in Architectura Artis Lullianae, inserta Thesauro ejus Artis Memorativae pag. 47 et seqq.zur Übersetzung des Abschnitts
Sunt autem termini simplices hi: I. Attributa absoluta: Bonitas, Magnitudo, Duratio, Potestas, Sapientia, Voluntas, Virtus, Veritas, Gloria; II. Relata: Differentia, Concordantia, Contrarietas, Principium, Medium, Finis, Majoritas, Aequalitas, Minoritas; III. Quaestiones: Utrum, Quid, de Quo, Quare, Quantum, Quale, Quando, Ubi, Quomodo (cum Quo); IV. Subjecta: Deus, Angelus, Coelum, Homo, Imaginatio, Sensitiva, Vegetativa, Elementativa, Instrumentativa; V. Virtutes: Justitia, Prudentia, Fortitudo, Temperantia, Fides, Spes, Charitas, Patientia, Pietas; VI. Vitia: Avaritia, Gula, Luxuria, Superbia, Acedia, Invidia, Ira, Mendacium, Inconstantia. Etsi Jan. Caecilius Frey Via ad Scient. et art. part. XI. c. 1. classem 3tiam et 6tam omittat.
zur Übersetzung des Abschnitts
Cum igitur in singulis classibus sint 9 res, et 9 rerum sint complexiones simpliciter 511, totidem in singulis classibus complexiones erunt, porro ducendo classem in classem per prob. 3. 511. 511. 511. 511. 511. ᴖ 511, f. 17804320388674561. Zensicub. de 511. Ut omittam omnes illas variationes, quibus idem terminus repetitur, item quibus una classis repetitur, seu ex una classe termini ponuntur plures.
zur Übersetzung des Abschnitts
Et hae solum sunt complexiones, quid dicam de Variationibus Situs, si in complexiones ducantur. Atque hic explicabo obiter problema hoc: Variationes situs seu dispositiones ducere in complexiones, seu datis certis rebus omnes variationes tam complexionis seu materiae, quam situs seu formae reperire. Sumantur omnes complexiones particulares dati numeri (v. g. de numero 4: uniones 4, com2nationes 6, con3nationes 4, con4natio 1) quaeratur variatio dispositionis singulorum exponentium per probl. 4. infra (v. g. 1 dat l, 2 dat 2, 3 dat 6, 4 dat 24), ea multiplicetur per complexionem suam particularem, seu de dato exponente (v. g. l ᴖ 4 f. 4, 2 ᴖ 6 f. 12, 4 ᴖ 6 f. 24, 1 ᴖ 24 f. 24). Aggregatum omnium factorum erit factus ex ductu dispositionum in complexiones, id est quaesitum (v. g. 4. 12. 24. 24.+ f. 64)." Verum in terminis Lullianis multa desidero.
zur Übersetzung des Abschnitts
Nam tota ejus methodus dirigitur ad artem potius ex tempore disserendi, quam plenam de re data scientiam consequendi, si non ex ipsius Lullii, certe Lullistarum intentione. Numerum Terminorum determinavit pro arbitrio, hinc in singulis classibus sunt novem. Cur praedicatis absolutis, quae abstractissima esse debent, commiscuit Voluntatem, Veritatem, Sapientiam, Virtutem, Gloriam, cur Pulchritudinem omisit, seu Figuram, cur Numerum? Praedicatis relatis debebat accensere multo plura, v. g. Causam, totum, partem, requisitum etc. Praeterea Majoritas, Aequalitas, Minoritas est nihil aliud, quam concordantia et differentia magnitudinis. Quaestionum tota classis ad praedicata pertinet: Utrum sit, est existentiae, quae durationem ad se trahit; Quid, essentiae; Quare, causae; de Quo, objecti; Quantum, magnitudinis; Quale, qualitatis, quae est genus praedicatorum absolutorum; Quando, temporis; Ubi, loci; Quomodo, formae; Cum Quo, adjuncti: omnes terminorum sunt, qui aut relati sunt inter praedicata, aut referendi. Et cur Quamdiu omisit, an ne durationi coincideret? cur igitur alia aeque coincidentia admiscet; denique Quomodo et cum Quo, male confuduntur.
zur Übersetzung des Abschnitts
Classes vero ultimae Vitiorum et Virtutum sunt prorsus ad scientiam hanc tam generalem ἀπροσδιόνυσοι. Ipsa quoque earum recensio quam partim manca, partim superflua! Virtutum recensuit priores 4 cardinales, mox 3 theologicas, cur igitur addita Patientia, quae in fortitudine dicitur contineri; cur Pietatem, id est amorem Dei, quae in Charitate? scilicet ut novenarii hiatus expleretur. Ipsa quoque Vitia cur non Virtutibus opposita recensuit? An ut intelligeremus in virtute vitia opposita, et in vitio virtutem? at in vitia 27 prodibunt. Subjectorum census placet maxime. Sunt enim hi inprimis Entium gradus: Deus, Angelus, Coelum (ex doctrina peripatetica Ens incorruptibile), Homo, Brutum perfectius (seu habens imaginationem), imperfectius (seu sensum solum, qualia de ζωοφύτοις narrant), Planta. Forma communis corporum (qualis oritur ex commixtione Elementorum, quo pertinent omnia inanima). Artificalia (quae nominat instrumenta). Haec sunt quorum complexu Lullius utitur, de quo judicium, maturum utique, gravis viri Petri Gassendi Logicae suae Epicureae T. 1. operum capite peculiari. Quare artem Lullii dudum com2natorium appellavit Jordan. Brunus Nolanus Scrutin. praefat. p. m. 684.
zur Übersetzung des Abschnitts
Atque hinc esse judico, quod immortalis Kircherus suam illam diu promissam artem magnam sciendi, seu novam portam scientiarum, qua de omnibus rebus infinitis rationibus disputari, cunctorumque summaria cognitio haberi possit (quo eodem fere modo suam Syntaxin artis mirabilis inscripsit Petr. Gregor. Tholosanus) Com2natoriae titulo ostentaverit. Unum hoc opto, ut ingenio vir vastissimo altius quam vel Lullius vel Tholosanus penetret in intima rerum, ac quae nos praeconcepimus, quorum lineamenta duximus, quae inter desiderata ponimus, expleat, quod de fatali ejus in illustrandis scientiis felicitate desperandum non est. Ac nos profecto haec non tam Arithmeticae augendae, et si et hoc fecimus, quam Logicae inventivae recludendis fontibus destinavimus, fugientes praeconis munere, et quod in catalogo desideratorum suis augmentis Scientiarum Verulamius fecit, satis habituri, si suspicionem tantae artis hominibus faciamus, quam cum incredibili fructu generis humani alius producat.
zur Übersetzung des Abschnitts
Quare age tandem artis complicatoriae (sic enim malumus, neque enim omnis complexus com2natio est) uti nobis constituenda videatur, lineamenta prima ducemus. Profundissimus principiorum in omnibus rebus scrutator Th. Hobbes merito posuit omne opus mentis nostrae esse computationem, sed hae vel summam addendo vel subtrahendo differentiam colligi; Elem. de Corp. p. l. c. 1. art. 2. Quemadmodum igitur duo sunt Algebraistarum et Analyticorum primaria signa + et -, ita duae quasi copulae est et non-est: illic componit mens, hic dividit. In tali igitur sensu τὁ Est non est proprie copula, sed pars praedicati; duae autem sunt copulae, una nominata, non, altera innominata, sed includitur in τῷ est, quoties ipsi non additum: non, quod ipsum fecit, ut τὁ Est habitum sit pro copula. Possemus adhibere in subsidium vocem: revera, v. g. Homo revera est animal. Homo non est lapis. Sed haec obiter.
zur Übersetzung des Abschnitts
Porro ut constet ex quibus omnia conficiantur, ad constituenda hujus artis praedicamenta et velut materiam analysis adhibenda est. Analysis haec est:
- Datus quicunque terminus resolvatur in partes formales, seu ponatur ejus definitio; partes autem hae iterum in partes, seu terminorum definitionis definitio; usque ad partes simplices seu terminos indefinibiles. Nam ού δεἰ παντὀς ὃρον ζητεἰν; et ultimi illi termini non jam amplius definitione, sed analogia intelliguntur.
- Inventi omnes termini primi ponantur in una classe, et designentur notis quibusdam; commodissimum erit numerari.
- Inter terminos primos ponantur non solum res, sed et modi sive respectus.
- Cum omnes termini orti varient distantia a primis, prout ex pluribus terminis primis componuntur, seu prout est exponens Complexionis, hinc tot classes faciendae, quot exponentes sunt, et in eandem classem conjiciendi termini, qui ex eodem numero primorum componuntur.
- Termini orti per com2nationem scribi aliter non poterunt, quam scribendo terminos primos, ex quibus componuntur, et quia termini primi signati sunt numeris, scribantur duo numeri duos terminos signantes.
- At termini orti per con3nationem aut alias majoris etiam exponentis Complexiones, seu termini qui sunt in classe 3tia et sequentibus, singuli toties varie scribi possunt, quot habet complexiones simpliciter exponens ipsorum spectatus non jam amplius ut exponens, sed ut numerus rerum. Habet hoc suum fundamentum in Usu IX, v. g. sunto termini primi his numeris signati 3, 6, 7, 9; sitque terminus ortus in classe tertia, seu per con3nationem compositus, nempe ex 3bus simplicibus 3, 6, 9, et sint in classe 2da combinationes hae: [1] 3. 6. [2] 3. 7. [3] 3. 9. [4] 6. 7. [5] 6. 9. [6] 7. 9. Ajo termini illum datum classis 3tiae scribi posse vel sic: 3. 6. 9, exprimendo omnes simplices; vel exprimendo·unum simplicem, et loco caeterorum duorum simplicium scribendo com2nationem, v. g. sic: ½. 9. vel 3⁄2. 6, vel sic: 5⁄2. 3. Hae quasi-fractiones quid significent, mox dicetur. Quo autem classis a prima remotior, hoc variatio major. Semper enim termini classis antecedentis sunt quasi genera subalterna ad terminos quosdam variationis sequentis.
- Quoties terminus ortus citatur extra suam classem, scribatur per modum fractionis, ut numerus superior seu numeratori sit numerus loci in classe; inferior seu nominator, numerus classis.
- Commodius est, in terminis ortis exponendis non omnes terminos primos, sed intermedios scribere, ob multitudinem, et ex iis eos qui maxime cogitanti de re occurrunt. Verum omnes primos scribere est fundamentalius.
- His ita constitutis possunt omnia subjecta et praedicata inveniri, tam affirmativa quam negativa, tam universalia quam particularia. Dati enim subjecti praedicata sunt omnes termini primi ejus; item omnes orti primis propiores, quorum omnes termini primi sunt in dato. Si igitur terminus datus, qui subjectum esse debet, scriptus est termnis primis, facile est eos primos, qui de ipso praedicantur, invenire, ortos vero etiam invenire dabitur, si in complexionibus disponendis ordo servetur. Sin terminus datus scriptus est ortis, aut partim ortis, partim simplicibus, quicquid praedicabitur de orto ejus, de dato praedicabitur. Et haec quidem omnia praedicata sunt latioris de angustiori, praedicatio vero aequalis de aequali est, quando definitio de termino, id est vel omnes termini primi ejus simul, vel orti, aut orti et simplices, in quibus omnes illi primi continentur, praedicantur de dato. Eae sunt tot, quot modis nuperrime diximus, unum Terminum scribi posse.
zur Übersetzung des Abschnitts
Ex his jam facile erit, numeris investigare omnia praedicata, quae de omni dato subjecto praedicari possunt, seu omnes U A. Propositiones de dato subjecto, nimirum singularum classium a prima usque ad classem dati inclusive; numeri ipsas denominantes seu exponentes ponantur ordine v. g. 1. (de classe prima) 2, (de 2da) 3. 4. etc. Unicuique tamquam non jam amplius exponenti, sed numero assignetur sua complexio simpliciter, v. g. 1. 3. 7. 15; quaerantur complexiones particulares numeri classis ultimae seu de qua est terminus datus, v. g. de 4, cujus complexio simpliciter 15, uniones 4, com2nationes 6, con3nationes 4, con4natio 1; singulae complexiones simpliciter classium multiplicentur per complexionem particularem classis ultimae, quae habeat exponentem eundem cum numero suae classis, v. g. 1 ᴖ 4 f. 4, 3 ᴖ 6 f. 18, 4 ᴖ 7 f. 28, 15 ᴖ 1 f. 15; aggregatum omnium factorum erit numerus omnium praedicatorum de dato subjecto, ita ut propositio sit U A, v. g. 4. 18. 28. 15. + f. 65.
zur Übersetzung des Abschnitts
Praedicata per propositionem PA seu numerus propositionum particularium affirmativarum ita investigabitur: inveniantur praedicata U A dati termini, uti nuper dictum est, et subjecta U A, uti mox dicetur; addatur numerus uterque, quia ex UA propositione oritur PA, tum per conversionem simpliciter, tum per subalternationem; productum erit quaesitum.
zur Übersetzung des Abschnitts
Subjecta in propositione UA dati termini sunt tum omnes termini orti, in quibus terminus datus totus continetur, quales sunt solum in classibus sequentibus, et hinc oritur subjectum angustius, tum omnes termini orti qui eosdem cum dato habent terminos simplices, uno verbo ejusdem termini definitiones, seu variationes eum scribendi, invicem sunt sibi subjecta aequalia.
zur Übersetzung des Abschnitts
Numerum subjectorum sic computabimus: inveniatur numerus omnium classium. Eae autem sunt tot, quot termini sunt primi in prima classe, v. g. sunt termini in prima classe tantum 5, erunt classes in universum 5, nempe in 1ma uniones, in 2da com2nationes, in 3tia con3nationes, in 4ta con4nationes, in 5ta con5nationes. Ita erit inventus etiam numerus omnium classium sequentium, subtrahendo numerum classis termini dati, v. g. 2 de numero classium in universum 5 remanebit 3. Numerum autem classium seu terminorum primorum supponamus pro numero rerum, numerum classis pro exponente, erit numerus terminorum in classe idem cum complexionibus particularibus dato numero et exponente, v. g. de 5 rebus uniones sunt 5, com2.3nationes 10, con4nationes 5, con5natio l; tot igitur erunt in singulis classibus exponenti correspondentibus termini, supposito quod termini primi sint 5. Praeterea Terminus datus, cujus subjecta quaeruntur, respondebit capiti complexionum; Subjecta angustiora ipsis complexionibus quarum datum est caput. Igitur: dati termini subjecta angustiora inveniemus, si problema hoc solvere poterimus:
zur Übersetzung des Abschnitts
"Dato capite complexiones invenire, partim simpliciter (ita inveniemus subjecta angustiora omnia) partim particulares, seu dato exponente (ita inveniemus ea tantum quae sunt in data classe). Problema hoc statim impraesentiarum solvemus, ubi manifestus ejus usus est, ne ubi seorsim posuerimus, novis exemplis indigeamus. Solutio igitur haec est: Subtrahatur de numero rerum, v. g. 5: a. b. c. d. e. exponens capitis dati, v. g. a. b, 2-5 f. 3 aut a, 1-5 f. 4. Sive supponamus datum caput unionem sive com2nationem esse; complexio enim ut sit necesse est. Propositio item exponente subtrahatur, de eo itidem exponens capitis dati. Igitur si datus sit quicunque exponens, in cujus complexionibus quoties datum caput reperiatur invenire sit propositum, quaeratur complexio exponentis tanto minoris dato, quantus est exponens capitis dati, in numero rerum, qui sit itidem tanto minor dato, quantus est exponens capitis dati per tabella א probl. l, inventum erit quod quaerebatur. At si Complexiones simpliciter capitis dati in omnibus complexionibus dati numeri quocunque exponente, quaerere propositum sit, complexio numeri rerum, numero dato tanto minoris, quantus est exponens capitis dati, erit quaesitum."
zur Übersetzung des Abschnitts
E. g. in 5 rerum a. b. c. d. e. unionibus datum caput a reperitur 1 vice (quae est nullio, seu ollio de 4); datum caput a. b. 0lla vice (quae est super 0llio, ut ita dicam, de 3); in com2nationibus earundem illud reperitur vicibus 4 (quae sunt uniones de 4) hoc 1 (quae est 0llio de 3), in con3nationibus illud 6 (com2natio de 4) hoc 3 (unio de 3), in con4nationibus illud 4 (con3natio de 4) hoc 3 (com2natio de 3), in con5nationibus utrobique 1 vice, (illic con4natio, hic con3natio de 3).
zur Übersetzung des Abschnitts
Hae complexiones sunt dato exponente, et quarum aggregatione oriuntur complexiones simpliciter, sed et sic: in 5 rerum complexionibus simpliciter (quae sunt 3) a reperitur vicibus 15 (complexio simpliciter de 4), ab 7 (complexio simpliciter de 3) vicibus. Hae complexiones sunt numerus subjectorum angustiorum dati termini. Subjecta aequalia, quando definitiones definitionibus subjiciuntur, eadem methodo inveniuntur qua supra praedicata aequalia. Termini enim aequales sunt servata quantitate et qualitate convertibiles, igitur ex praedicatis fiunt subjecta et contra, praedicata autem tot sunt, quot dati termini (cujus subjecta quaeruntur) termini primi habent complexiones simpliciter, v. g. + a 1, ab 2. Additis jam subjectis aequalibus ad angustiora l + 15 f. 16, 2 + 7 f. 9, prodibit numerus subjectorum omnium dati termini, quem erat propositum invenire. Subjecta hactenus universalia, restant particularia, ea tot sunt quot praedicata particularia.
zur Übersetzung des Abschnitts
Praedicata et subjecta negativa sic invenientur: computentur ex datis certis terminis primis tanquam numero rerum omnes termini tam primi quam orti, tanquam complexiones simpliciter, v. g. si termini primi sint 5, erunt 31; de producto detrahantur omnia praedicata affirmativa universalia et subjecta angustiora affirmativa universalia: residuum erunt omnia praedicata negativa. De subjectis contra. Particularia negativa ex universalibus computentur, uti supra PA ex UA computavimus. Omisimus vero propositiones identicas UA, quarum sunt tot quot complexiones simpliciter Terminorum primorum, seu quot sunt omnino termini et primi et orti, quia quilibet terminus vel primus vel ortus de se dicitur. Caeterum inter complexiones illas omisimus, in quibus idem terminus repetitur, quae repetitio in nonnullis producit variationem in infinitum, ut in numeris et figuris geometriae.
zur Übersetzung des Abschnitts
Methodus porro argumenta inveniendi haec est: Esto datus quicunque terminus tanquam subjectum A et alius quicunque tanquam praedicatum B. quaeratur medium: Medium erit praedicatum subjecti et subjectum praedicati, id est terminus quicunque continens A et contentus a B. Continere autem terminus terminum dicitur, si omnes ejus termini primi sunt in illo. Fundamentalis autem demonstratio est, si uterque terminus resolvatur in primos, manifestum erit alterum alterius aut partem esse, aut partium earundem. Mediorum autem numerum sic inveniemus: Subjectum et praedicatum vel sunt in eadem classe, vel diversa. Si in eadem, necesse est utrumque terminum esse ortum, et variationem scriptionis saltem seu definitionis ejusdem termini, poterunt igitur duae definitiones ejusdem termini non nisi per tertiam de se invicem probari. Igitur de numero definitionum ejusdem termini orti, quem investigavimus supra n. 69 subtrahatur 2, residuum erit numerus mediorum possibilium inter terminos aequales.
zur Übersetzung des Abschnitts
Sin non sunt in eadem classe, erit praedicatum in classe minoris exponentis, subjectum in classe majoris. Jam supponatur Praedicatum velut caput complexionis, exponens classis subjecti supponatur pro numero rerum. Inveniantur omnes complexiones dati capitis particulares per singulas classes a classe praedicati ad classem subjecti inclusive; in singulis classibus complexiones dati capitis particulares ducantur in complexiones simpliciter exponentis ipsius classis pro numero rerum suppositi. Aggregatum omnium factorum, subtracto 2, erit quaesitum.
zur Übersetzung des Abschnitts
Praedicatum autem de subjecto negari facile inveniemus, si utroque termino in primos resoluto manifestum est neutrum altero contineri. Probari tamen negativa sic poterit: inveniantur omnia praedicata subjecti, cum de omnibus negetur praedicatum, totidem erunt media probandi negativam. Inveniantur omnia subjecta praedicati, cum omnia negentur de subjecto, etiam erunt totidem media probandi negativam. Utrisque igitur computatis numerum mediorum probandi negativam habebimus.
zur Übersetzung des Abschnitts
Admovendum denique est, totam hanc artem complicatoriam directam esse ad theoremata, seu propositiones quae sunt aeternae veritatis, seu non arbitrio Dei, sed sua natura constant. Omnes vero propositiones singulares quasi historicae, v. g. Augustus fuit Romanorum Imperator, aut observationes, id est propositiones univerales, sed quarum veritas non in essentia, sed existentia fundata est, quaeque verae sunt quasi casu, id est Dei arbitrio, v. g. omnes homines adulti in Europa habent cognitionem Dei. Talium non datur demonstratio, sed inductio, nisi quod interdum observatio per observationem interventu Theorematis demonstrari potest.
zur Übersetzung des Abschnitts
Ad tales observationes pertinent omnes propositiones particulares, quae non sunt conversae vel subalternae universalis. Hinc igitur manifestum est, quo sensu dicatur singularium non esse demonstrationem, et cur profundissimus Aristoteles locos argumentorum posuerit in Topicis, ubi et propositiones sunt contingentes et argumenta probabilia, Demonstrationum autem unus locus est: definitio. Verum cum de re dicenda sunt ea quae non ex ipsius visceribus desumuntur, v. g. Christum natum esse Bethleemi, nemo huc definitionibus deveniet, sed historiae materiam, loci reminiscentiam suppeditabunt. Haec jam locorum Topicorum origo, et in singulis maximarum, quibus omnibus qui sint fontes, ostenderemus itidem, nisi timeremus ne in progressu sermonis cupiditate declarandi omnia abriperemur.
zur Übersetzung des Abschnitts
Uno saltem verbo indigitabimus, omnia ex doctrina metaphysica relationum Entis ad Ens repetenda esse, sic ut ex generibus quidem relationum Loci, ex theorematis autem singulorum maximae efformentur. Hoc vidisse arbitror, praeter morem compendiographorum solidissimum Joh. Henr. Bisterfeld in Phosphoro Catholico seu Epitome artis meditandi ed. Lugd. Bat. anno 1657, quae tota fundatur in immeatione et περιχορἡσει, ut vocat, universali omnium in omnibus, similitudine item et dissimilitudine omnium cum omnibus, quarum principia: Relationes.
zur Übersetzung des Abschnitts
Eum libellum qui legerit, usum artis complicatoriae magis magisque perspiciet. Ingeniosus ille, quem saepe nominavimus, Joh. Hospinianus, libellum promisit de inveniendi et judicandi facultatibus, in quo emendationem doctrinae Topicae paraverat, locosque recensuerat 180, maximas 2796, vide controvers. dial. p. 442. Hunc ego insigni rei logicae damno nunquam editum arbitror. Abibimus hinc, cum primum γεῶμα quoddam praxeos artis com2natoriae dederimus.
zur Übersetzung des Abschnitts
Commodissima Mathesis extemporaneo conatui visa est: hinc non a primis simpliciter terminis orsi sumus, sed a primis in mathesi; neque omnes posuimus, sed quos ad producendos complicatione sua terminos ortos propositos sufficere judicabamus. Potuissemus eadem methodo omnes definitiones ex Elementis Euclidis exponere, si tempus superfuisset. Quoniam autem non a primis simpliciter terminis orti sumus, hinc necessarium erat signa adhibere, quibus casus vocabulorum aliaque ad sermonem complendum necessaria intelligentur. Nam siquidem a primis simpliciter terminis incepissemus, pro ipsis casuum variationibus, quorum ex relationibus et metaphysica originem exposuit Jul. Caesar Scaliger lib. de Caus. L. L. terminos posuissemus. Adhibuimus autem articulos graecos. Numerum pluralem signavimus adscripto in ( ), 15 si quidem indefinitus, 2, 3 etc. si determinatus.
zur Übersetzung des Abschnitts
Esto igitur Classis I. in qua termini primi: 1. punctum, 2. spatium, 3. intersitum, 4. adsitum seu contiguum, 5. dissitum seu distans, 6. terminus seu quae distant, 7. insitum, 8. inclusum (v. g. centrum est insitum circulo, inclusum peripheriae), 9. pars, 10. totum, 11. idem, 12. diversum, 13. unum, 14. numerus, 15. plura, v. g. l. 2. 3. 4. 5 etc., 16. distantia, 17. possibile, 18. omne, 19. datum, 20. Fit, 21. regio, 22. dimensio, 23. longum, 24. latum, 25. profundum, 26. commune, 27. progressio seu continuatum. Classis II. l. Quantitas est 14 τῶν 9 (15), 2, Includens est 6. 10. III. l, Intervallum est 2. 3. 10. 2. Aequale A τῆς 11. ½ 3. Continuum est A ad B, si τοῦ A ἠ 9 est 4 et 7 τῷ B. IV. 1. Majus est A habens τἠν 9. 2⁄3 τῷ B. 2. Minus, B 2⁄3 τῆ 9 τοῠ A. 3. Linea, ⅓ τῶν l (2). 4, Parallelum. 2⁄3 ἐν τῇ 16. 5. Figura. 24. 8, ab 18. 21. V. 1, Crescens, quod 20. 3⁄4 2, Decrescens, 20. 2⁄4. 3, Implexum est 2⁄3 in τῇ 11. 22. 4, Secans, 3⁄2 in τῇ 12. 22. VI. l, Convergens, 2⁄5 ἐν τῇ 16. 2. Divergens, 1⁄5 ἐν τῇ 16. VII. 1. Superficies, ⅓ τῶν 2⁄3 2, Infinitum, ¼ quam 18. 19. 17. 3. Peripheria, ¼. 13. 2⁄3. 4. A dicitur Mensura seu metitur B si 10 ex A (15) 2⁄3 est 2⁄3 τῷ B. VIII. 1. Maximum est ¼ non 2⁄4.· 2. Minimum, 2⁄4 non ¼.· 3. Recta, 3⁄4. 2⁄3. τῇ 16. τῷν 6 (2). 4. quae non talis, Curva. 5. Arcus, 9 τῆς 3⁄7. IX. 1. Ambitus est 1⁄7. 2⁄2. X. 1. Commensurabilia sunt, quorum 4⁄7. 26 est et l et 2. XI. 1. Angulus est quem faciunt 3⁄4 (2). 4, 2⁄6. XII. 1. Planum est 1⁄7 ⅔. τῇ 16 τῷν 6. XIII. l. Gibbus, 1⁄7. ¼.·τῇ 16 τῷν 6. XIV. 1. Rectilinaeum est 5⁄4 cujus ⅔ est τῷν 3⁄8 (15). 2. quae dicuntur Latera. 3. si 3⁄5 (3), Triangulum. 4. Si 3⁄8 (4), Quadrangulum etc. XV. l. Lunula est ⅓ τῷν 5⁄8 (2), non ⅔ 4 (2). [subintelligo autem tam lunulam gibbosam, qua arcus arcui concavitatem obvertit, quam falcatam qua interior alterius concavitati suam convexitatem] XVI. l. Angulus rectus est 1⁄12. ⅔. in τῷ 18. 21. 2. Segmentum est 3 τὀν ⅔ et 3⁄8 7 τῇ 5⁄4. XVII. l. Aequilaterum est 5⁄4 cujus ⅔ est 8 τῷν 3⁄8 (15). 2. Triangulum aequicrurum est 5⁄4 cujus ⅔ est τῷν 3⁄8 (3) ⅔ 2. 3. Scalenum est 5⁄4 cujus ⅔ est τῷν 3⁄5 (3) non ⅔ (3). X VIII. l. Angulus contactus est quem, faciunt ¾ (2. 4 2⁄6 non ⅔.· 27. modo 17. XIX. l. Inscriptum est 4⁄5. 7 cujus 1⁄11 (15) sunt 4 τῷ·⅔. 2. Circumscripta vero est ea figura cui inscripta est. XX. 1. Angulus obtusus est ¼ quam 1⁄15.·2. Acutus, 2⁄4 quam 1⁄16. XXI. 1. Diameter est 3⁄8. 1⁄8 7. τῇ ¾. XXII. l. Circulus est 1⁄17. 8. ab 18. 21. habens τἠν 16. ⅔ τοῡ 19 alicujus l (quod dicitur 2 Centrum Circuli) ab 18. 6. 2. Triangulum rectangulum est 5⁄4 cujus 1⁄11 (3) sunt omnes, sed 13, est ⅔ in τῷ 18. 21. XXIII. l. Centrum Figurae est 1. 26 τοῐς 1⁄21 (15). XXIV. 1. Semifigura data v. g. semicirculus etc. est 3 τὀν 1⁄22 et (dimidium τοῡ) ⅔. Hinc facile erit definitiones conficere, si observetur, quod n. 70 diximus in iis notis, quae per fractiones scriptae sunt: nominatorem, designare numerum classis, numeratorem, numerum termini in classe, v. g. centrum est 1. (punctum) 26 (commune: τοῐς 1⁄21 (diametris) 15 pluribus. Diameter est 3⁄8 (recta) 1⁄5 (maxima) 7 (insita) τῇ 5⁄4 (figurae).
zur Übersetzung des Abschnitts
Ex his, quae de Arte complicatoria Scientiarum, seu Logica inventiva disseruimus, cujus quasi praedicamenta ejusmodi Terminorum tabula absolverentur, fluit velut Porisma seu usus XI: Scriptura Universalis, id est cuicunque legenti, cujuscunque linguae perito intelligibilis, qualem hodie complures viri eruditi tentarunt, quorum diligentissimus Caspar Schottus hos recenset lib. 7. Techn. Curios., primo Hispanum quendam, cujus meminerit Kenelm. Digbaeus tr. de Nat. Corp. c. 28. n. 8. quique fuerit Romae anno 1653, ejus methodus haec ex ipsa natura rerum satis ingeniose petita: distribuebat res in varias classes, in qualibet classe erat certus numerus rerum. Ita meris numeris scribebat, citando numerum classis et rei in classe, adhibitis tamen notis quibusdam flexionum grammaticarum et orthographicarum. Idem fieret per classes a nobis praescriptas fundamentalius, quia in iis fundamentalior digestio est. Deinde Athanasium Kircherum, qui Polygraphiam suam novam et universalem dudum promisit; denique Joh. Joachimum Becherum, Archiatrum Moguntinum, opusculo primum Francofurti latine edito, deinde germanice anno 1661 is requirit, ut construatur Lexicon Latinum, tanquam fundamentum, et in eo disponantur voces ordine pure alphabetico et numerentur; fiant deinde Lexica, ubi voces in singulis linguis dispositae non alphabetice, sed quo ordine Latinae dispositae sunt ipsis respondentes. Scribantur igitur quae ab omnibus intelligi debent, numeris, et qui legere vult, is evolvat in lexico suo vernaculo vocem dato numero signatam, et ita interpretabitur. Ita satis erit legentem vernaculam intelligere et ejus Lexicon evolvere, scribentem necesse est (nisi habeat unum adhuc Lexicon suae linguae alphabeticum ad numeros se referens) et vernaculam et latinam tenere, et utriusque lexicon evolvere. Verum et Hispani illius et Becheri artificium et obvium et impracticabile est ob synonyma, ob vocum ambiguitatem, ob evolvendi perpetuum taedium (quia numeros nemo unquam memoriae mandabit), ob ὲτερογένειαν phrasium in linguis.
zur Übersetzung des Abschnitts
Verum constitutis Tabulis vel praedicamentis artis nostrae complicatoriae majora emergent. Nam termini primi, ex quorum complexu omnes alii constituuntur, signentur notis, hae notae erunt quasi alphabetum. Commodum autem erit notas quam maxime fieri naturales. v. g. pro uno punctum, pro numeris puncta, pro relationibus Entis ad Ens lineas, pro variatione angulorum aut terminorum in lineis genera relationum. Ea si recte constituta fuerint et ingeniose, scriptura haec universalis aeque erit facilis quam communis, et quae possit sine omni lexico legi, simulque imbibetur omnium rerum fundamentalis cognitio. Fiet igitur omnis talis scriptura quasi figuris geometricis, et velut picturis, uti olim Aegyptii, hodie Sinenses, verum eorum picturae non reducuntur ad certum Alphabetum seu literas, quo fit ut incredibili memoriae afflictione opus sit, quod hic contra est.
-
Hic igitur est Usus XI complexionum, in constituenda nempe polygraphia universali. XIImo loco constituemus jucundas quasdam partim contemplationes, partim praxes ex Schwenteri Deliciis Mathematicis et supplementis G. P. Harsdörfferi, quem librum publice interest continuari, haustas. P. 1. sect. 1. prop. 32 reperitur numerus complexionum simpliciter, quem faciunt res 23, v. g. literae Alphabeti, nempe 8388607. P. 2 sect. 4. prop. 7 docet dato textu melodias invenire, de quo nos infra probl. 6. Harsdörfferus parte ead. sect. 10. prop. 25 refert ingeniosum repertum Dni. de Breissac, qua nihil potest arti scientiarum complicatoriae accommodatius reperiri.
zur Übersetzung des Abschnitts
Is, quaecunque in re bellica attendere bonus imperator debet, ita complexus est: facit classes novem, in 1ma quaestiones et circumstantias, in IIda status, in III. personas, in IV. actus, in V. fines, in VI. instrumenta exemtae actionis, seu quibus uti in nostra potestate est, facere autem ea, non est; VII. instrumenta quae et facimus et adhibemus; VIII. instrumenta quorum usus consumtio est; IX. actos finales seu proximos executioni, v. g.
1. An. Cum quo. Ubi. Quando. Quomodo. Quantum. 2. Bellum. Pax. Induciae. Colloquium. Foedus. Transactio. 3. Patriotae. Subditi. Foederati. Clientes. Neutrales. Hostes. 4. Manere. Cedere. Pugnare. Proficisci. Expeditio. Hyberna. 5. Decus. Lucrum. Obedientia. Honestas. Necessitas. Commoditas. 6. Sol. Aqua. Ventus. Itinera. Angustiae. Occasio. 7. Cursus. Scalae. Pontes. Ligones. Palae. (𝔖𝔠𝔥𝔞𝔲𝔣𝔣𝔢𝔩𝔫) Naves. 8. Pecunia. Commeatus. Pulvis Torm. Globi Torm. Equi. Medicamenta. 9. Excubiae. Ordo. Impressio. Securitas. Aggressio. Consilia. zur Übersetzung des Abschnitts
Fiant novem rotae ex papyro, omnes concentricae et se invicem circumdantes, ita ut quaelibet reliquis immotis rotari possit. Ita promota leviter quacunque rota nova quaestio, nova complexio prodibit. Verum cum hic inter res ejusdem classis non detur complexio atque ita accurate loquendo non sit complexio terminorum cum terminis, sed classium cum classibus, pertinebit computatio variationis ad probl. 3. Quoniam tamen complexio etiam, quae hujus loci est, potest repraesentari rotis, ut mox dicemus, fecit cognatio, ut praeoccuparemus. Sic igitur inveniemus: multiplicetur 6 in se novies: 6. 6. 6. 6. 6. 6. 6. 6 ᴖ 6. seu quaeratur progressio geometria sextupla, cujus exponens 9, aut cubicubus de 6. f. 18077696; tantum superest, ut sint solum 216 quaestiones, quod putat Harsdörffer.
zur Übersetzung des Abschnitts
Caeterum quoties in complexionibus singuli termini in singulos ducuntur, ibi necesse est tot fieri rotas, quot unitates continet numerus rerum : deinde necesse est singulis rotis inscribi omnes res. Ita variis rotarum conversionibus complexiones innumerabiles gignentur, eruntque omnes complexiones quasi jam scriptae seorsim, quibus revera scribendis vix grandes libri sufficient.
zur Übersetzung des Abschnitts
Sic ipsemet doctissimus Harsdörff. P. 13. sect. 4. prop. 5. machinam 5 rotarum concentricarum construxit, quam vocat 𝔉𝔲𝔢𝔫𝔣𝔣𝔞𝔠𝔥𝔢𝔫 𝔇𝔢𝔫𝔨𝔯𝔦𝔫𝔤 𝔡𝔢𝔯 𝔱𝔢𝔲𝔱𝔰𝔠𝔥𝔢𝔫 𝔖𝔭𝔯𝔞𝔠𝔥𝔢, ubi in rota intima sunt 48 𝔙𝔬𝔯𝔰𝔶𝔩𝔟𝔢𝔫, in penultima 60 𝔄𝔫𝖋𝔞𝔫𝔤𝔰- 𝔲𝔫𝔡 ℜ𝔢𝔦𝔪𝔟𝔲𝔠𝔥𝔰𝔱𝔞𝔟𝔢𝔫, in media 12 𝔐𝔦𝔱𝔱𝔢𝔩-𝔅𝔲𝔠𝔥𝔰𝔱𝔞𝔟𝔢𝔫, vocales nempe vel diphthongi, in penextima 120 𝔈𝔫𝔡-𝔅𝔲𝔠𝔥𝔰𝔱𝔞𝔟𝔢𝔫, in extima 24 𝔑𝔞𝔠𝔥𝔰𝔶𝔩𝔟𝔢𝔫. In has omnes voces germanicas resolvi contendit. Cum hic similiter classes sint in classes ducendae, multiplicemus: 48. 60. 12. 120. 24, factus ex prioribus per sequentem f. 97209600, qui est numerus vocum germanicarum hinc orientium utilium seu 96 significantium et inutilium.
zur Übersetzung des Abschnitts
Construxit et rotas Raym. Lullius, et in Thesauro artis memorativae Joh. Henr. Alstedius, cujus rotis, in quibus res et quaestiones, adjecta est norma mobilis, in qua loci Topici, secundum quos de rebus disseratur, quaestiones probentur; et fraternitas Roseae Crucis in fama sua promittit grandem librum titulo Rotae Mundi, in quo omne scibile contineatur. Orbitam quandam pietatis, ut vocat, adjecit suo Veridico Christiano Joh. Davidius Soc. J. Ex eodem principio complicationum est Rhabdologia Neperi, et pensiles illae Serae, die 𝔙𝔬𝔯𝔩𝔢𝔤-𝔖𝔠𝔥𝔩𝔬𝔢𝔰𝔰𝔢𝔯, quae sine clave mirabili arte aperiuntur, vocant 𝔐𝔞𝔥𝔩-𝔖𝔠𝔥𝔩𝔬𝔰𝔰𝔢𝔯, nempe superficies serae armillis tecta est, quasi annulis gyrabilibus, singulis annulis literae alphabeti inscriptae sunt. Porro serae certum nomen impositum est, v. g. Ursula, Catharina, ad quod nisi casu qui nomen ignorat, annulorum gyrator pervenire non potest. At qui novit nomen, ita gyrat annulos invicem, ut tandem nomen prodeat, seu literae alphabeti datum nomen conficientes sint ex diversis annulis in eadem linea, justa serie. Tum demum ubi in tali statu annuli erunt, poterit facillime sera aperiri. Vide de his Seris armillaribus Weckerum in Secretis, Illustrissimum Gustavum Selenum in Cryptographia fol. 449, Schwenterum in Deliciis sect. 15. prop. 25. Desinemus Usus problematis 1 et 2 enumerare, cum coronidis loco de coloribus disseruerimus. Harsdörfferus P. 3. Sect. 3. prop. 16 ponit colores primos hos 5: Albus, flavus, rubeus, caeruleus, niger.
zur Übersetzung des Abschnitts
Eos complicat ita tamen ut extremi: albus et niger, nunquam simul coeant. Oritur igitur ex AF subalbus, AR carneus AC cinereus; FR aureus, FC viridis, FN fuscus; RC purpureus, RN subrubeus; CN subcaeruleus. Sunt igitur 9, quot nempe sunt com2nationes 5 rerum, demta una, extremorum. Quid vero si tertii ordinis colores addantur, seu con3nationes primorum et com2nationes secundorum, et ita porro, quanta multitudo exsurget? Hoc tamen admoneo, ipsos tanquam primos suppositos non esse primos, sed omnes ex albi et nigri, seu lucis et umbrae mixtione oriri.
zur Übersetzung des Abschnitts
Ac recordor legere me, etsi non succurrit autor, nobilem acupictorem nescio quem 80 colores contexuisse, vicinosque semper vicinis junxisse, ex filis tamen non nisi nigerrimis ac non nisi albissimis, porro varias alternationes alborum nigrorumque filorum, et immediationes modo plurium alborum, modo plurium nigrorum, varietatem colorum progenuisse; fila vero singula per se inermi oculo invisibilia paene fuisse. Si ita est, fuisset hoc solum experimentum satis ad colorum naturam ab ipsis incunabulis repetendam.
Probl. III.
Dato numero classium et rerum in classibus, complexiones in classium inveniere.
"Complexiones autem classium sunt, quarum exponens cum numero classium idem est; et qualibet complexione ex qualibet classe res una. Ducatur numerus rerum unius classis in numerum rerum alterius, et si plures sunt, numerus tertiae in factum ex his, seu semper numerus sequentis in factum ex antecedentibus; factus ex omnibus continue, erit quaesitum."
zur Übersetzung des Abschnitts
Usus hujus problematis fuit tam in usu 6. probl. 1 et 2, ubi modos syllogisticos investigabamus, tum in usu 12, ubi et exempla prostant. Hic aliis utemur. Diximus supra, Complexionum doctrinam versari in divisionem generibus subalternis inveniendis, inveniendis item speciebus unius divisionis, et denique plurium in se invicem ductarum.
zur Übersetzung des Abschnitts
Idque postremum huic loco servavimus. Divisionem autem indivisionem ducere est unius divisionis membra alterius membris subdividere, quod interdum procedit vice versa, interdum non. Interdum omnia membra unius divisionis omnibus alterius subdividi possunt, interdum quaedam tantum, aut quibusdam tantum. Si vice versa, ita signabimus
| ⎧ | c | |||
| ⎧ | a | ⎥ | ||
| A | ⎨ | ⎨ | d | |
| ⎩ | b | ⎥ | ||
| ⎩ | e |
| si quaedam tantum, ita: | ⎧ | c | |||
| ⎧ | a | ⎨ | d | ||
| A | ⎨ | ⎥ | |||
| ⎩ | b | ⎩ | e |
| si quaedam quibusdam tantum, ita: | c | ||||
| ⎨ | |||||
| a | d | ||||
| A | ⎨ | ||||
| b | … | e |
Ad nostram vero computationem primus saltem modus pertinet, in quo exemplum suppetit ex Politicis egregium. A esto Respublica, a recta, b aberrans, quae est divisio moralis; c Monarchia, d Aristocratia, e Democratia, quae est divisio numerica: ducta divisione numerica in moralem, orientur species mixtae 2 ᴖ 3 f. 6, ac. ad. ae. bc. bd. be.
zur Übersetzung des Abschnitts
Hinc origo formulae hujus: divisionem in divisionem ducere, manifesta est, ducendus enim numerus specierum unius in numerum specierum alterius. Numerum autem in numerum ducere est numerum numero multiplicare, et toties ponere datum, quot alter habet unitates. Origo est ex geometria, ubi si linea aliam extremitate contingens ab initio ad finem ipsius movetur, si cur eam radat, spatium omne, quod occupabit linea mota, constituet figuram quadrangularem, si ad angulos rectos alteram contingit, ἐτερόμηκες aut quadratum: sin aliter, rhombum aut rhomboeides; si alteri aequalis, quadratum aut rhombum; sin aliter, ἐτηρόμηκες aut rhomboeides. Hinc et spatium ipsum quadrangulare facto ex multiplicatione lineae per lineam aequale est.
zur Übersetzung des Abschnitts
Caeterum ejusmodi divisionibus complicabilibus pleni sunt libri tabularum, oriunturque nonnunquam confusiones ex commixtione diversarum divisionum in unum, quod dividentibus conscientiam in rectam, erroneam, probabilem, scrupulosam, dubiam, factum videtur. Nam ratione veritatis in rectam et erroneam dispescitur, ratione firmitatis in apprehendendo incertam, probabilem, dubiam; quid autem aliud dubia, quam scrupulosa?
zur Übersetzung des Abschnitts
Hujus problematis etiam propria investigatio Varronis apud B. Augustinum lib. 19 de Civ. Dei cap. l, numeri sectarum circa summum bonum possibilium. Primum igitur calculum ejus sequemur, deinde ad exactius judicium revocabimus.
zur Übersetzung des Abschnitts
Divisiones sunt VI, 1ma quadrimembris, 2da et 6ta trimembris, reliquae bimembres. I. Summum Bonum esse potest vel Voluptas, vel Indoloria, vel utraque, vel prima naturae, 4. II. horum quodlibet vel propter virtutem expetitur, vel virtus propter ipsum, vel et ipsum et virtus propter se, 4 ᴖ 3. f. 12. III. S. B. aliquis vel in se quearit vel in societate 12 ᴖ 2. f. 24. IV. Opinio autem de S. B. constat vel apprehensione certa, vel probabili Academica, 24 ᴖ 2 f. V. 48. Vitae item genus cynicum vel cultum, 48 ᴖ 2 f. 96. VI. Otiosum, negotiosum vel temperatum, 96 ᴖ 3 f. 288. Haec apud B. Augustinum Varro cap. l; at c. 2 accuratiorem retro censum instituit. Divisionem ait 3, 5 et 6 facere ad modum prosequendi; 4 ad modum apprehendendi S. B.; corruunt igitur divisiones ultimae, et varietates 276, remanent 12. Porro capite 3. voluptatem, indoloriam et utramque ait contineri in Primis naturae. Remanent igitur 3. (corruunt 9) Prima naturae propter se, virtus propter se, utraque propter se. Postremam autem sententiam et quasi cribratione facta in fundo remanentem amplectitur Varro.
zur Übersetzung des Abschnitts
Ego in his, noto, Varronem non tam possibiles sententias colligere voluisse, quam celebratas, hinc axioma ejus: qui circa summum bonum differant, secta differre; et contra. Interim dum divisionem instituit, non potuit, quin quasdam ἀδεσπότους admisceret. Alioqui cur divisiones attulit, quas postea summi boni varietatem non facere agnoscit; an ut numero imperitis admirationem incuteret? Praeterea si genera·vitae admiscere voluit, cur non plura? nonne alii scientias sectantur, alii minime; alii professionem faciunt ex sapientia, creduntque hac imprimis summum Bonum obtineri? Etiam hoc ad S. B. magni momenti est, in qua quis republica vivat: alii vitam rusticam urbanae praetulere, suntque genera variationum infinita fere, in quibus singulis aliqui fuere, qui hac sola via crederent ad S. B. iri posse.
zur Übersetzung des Abschnitts
Porro quando prima divisio ducitur in 1mum membrum secundae facit 4 species: l. voluptas, 2. indoloria, 3. utraque, 4. prima naturae, propter virtutem, cum tamen in omnibus sit unum summum Bonum, Virtus; qui prima naturae, is et caetera; qui voluptatem, is et indoloriam ad virtutem referet. Adde quod erat in potestate Varronis, non solum 2dam et 6tam, sed et 3 et 4 et 5 trimembrem facere, addendo 3tiam speciem, semper mixtam ex duabus; v. g. in se vel in societate, vel utraque; apprehensione certa, probabili, dubia; cynicum, cultum, temperatum.
zur Übersetzung des Abschnitts
Fuit et sententia, quae negaret dari S. B. constans, sed faciendum quod cuique veniret in mentem, ad quod ferretur motu puro animi et irrefracto. Huc fere Academia nova, et hodiernus Anabaptistarum spiritus inclinabat. Ubi vero illi qui negant in hac vita culmen hoc ascendi posse? quod Solon propter incertitudinem pronunciandi dixit, Christiani philosophi ipsa rei natura moti. Valentinus vero Weigelius nimis enthusiastice, beatiudinem hominis esse Deificationem.
zur Übersetzung des Abschnitts
Apud illos quoque, quibus collocatur beatitudo in aeterna vita, alii asserunt, alii negant Visionem substantiae Dei beatificam. Hoc reformatos recordor facere, et extat de hoc argumento dissertatio inter Gisb. Voetii selectas; illud nostros, ac pro hac sententia scripsit Matth. Hoë ab Hoënegg peculiarem libellum contra Dnum. Budowiz a Budowa.
zur Übersetzung des Abschnitts
In hac quoque vita omnes illos omisit Varro, qui bonum aliquod externum, eorum quae fortunae esse dicunt, summum esse supponunt, quales fuisse, ipsa Aristotelis recensio indicio est. Corporis bona sane pertinent ad prima naturae, sed fieri potest ut aliquis hoc potissimum genus voluptatis sequatur, alius aliud. Et bonum animi jam aut habitus aut actio est, illud Stoicis, hoc Aristoteli visum. Stoicis hodie se applicuit accuratus sane vir, Eckardus Leichnerus, Medicus Erphordiensis, tr. de apodictica scholarum reformatione et alibi.
zur Übersetzung des Abschnitts
Quin et voluptatem animi pro S. B. habendam censet Laurentius Valla in lib. de Vero Bono, et ejus Apologia ad Eugenium IV, Pontificem Maximum, ac P. Gassendus in Ethica Epicuri, idque et Aristoteli excidisse VII. Nicomach. 12 et 13 observavit Cl. Thomasius Tab. Phil. Pract. XXX. lin. 58. Ad voluptatem animi gloriam, id est triumphum animi internum, sua laude sibi placentis, reducit Th. Hobbes initio librorum de cive. Fuere qui contemplationem actioni praeferrent, alii contra, alii utramque aequali loco posuere. Breviter quotquot bonorum imae sunt species, quotquot ex illis complexiones, tot sunt summi boni possibiles sectae numerandae.
zur Übersetzung des Abschnitts
Ex hoc ipso problemate origo est numeri personarum in singulis gradibus Arboris Consanguinitatis, eum nos, ne nimium a studiorum nostrorum summa divertisse videamur, eruemus. Computationem autem, canonica neglecta, civilem sequemur.
zur Übersetzung des Abschnitts
Duplex personarum in singulis gradibus enumeratio est, una generalis, altera specialis. In illa sunt tot personae quot diversi flexus cognationis, eadem tamen distantia. Flexus autem cognationis voco ipsa velut itinera in arbore consanguinitatis, lineas angulosque, dum modo sursum deorsumve, modo in latus itur. In hac non solum flexus cognationis varietatem facit, sed et sexus tum intermediarum, tum personae, cujus distantia quaeritur a data. In illa enumeratione Patruus, Amita; id est Patris frater sororve: Avunculus, Matertera, id est Matris frater sororque, habentur pro eadem persona, et convenientissime intelliguntur in voce Patrui, quia masculinus dignior foemininum comprehendit; sed in enumeratione speciali habentur pro 4 diversis personis. Igitur illic cognationes, hic personae numerantur (sic tamen ut plures fratres vel plures sorores, quia ne sexu quidem variant, pro una utrobique persona habeantur) Illa generalis computatio est Caji in l. 1 et 3 (quanquam specialis nonnunquam mixta est), haec specialis Pauli in grandi illa l. 10. D. de Grad. et Affinibus. Etsi autem prior fundata est in prob. l et 2, quia tamen posterioris fundamentum est, quae hoc pertinet, praemittemus.
zur Übersetzung des Abschnitts
Cognatio est formae linea vel linearum a cognata persona ad datam ductarum, ratione rectitudinis et inflexionis, et harum alternationis. Persona h. l. est persona datae cognationis et dati gradus, sexusque tum sui, tum intermediarum, inter cognatam scilicet et datam. Datum autem voco personam, eum eamve, de cujus cognatione quaeritur ut appellant JCti veteres; Joh. Andreae Petrucium nomine sui Bidelli fertur nominasse Fr. Hottomannus lib. de Gradib. Cognationum, ὐποϑετικὀν, latine Propositum.
zur Übersetzung des Abschnitts
Terminus est persona vel cognatio, quae est de conceptu complexae, v. g. frater est patris filius. Igitur Patris et Filius sunt termini, ex quibus conceptus Fratris componitur. Termini autem sunt vel primi, tales accurate loquendo sunt hi solum: Pater et filius, nos tamen commodioris computationis causa omnes personas lineae rectae vel supra vel infra supponemus pro primis, vel orti: accurate loquendo omnes qui plus uno gradu remoti sunt a dato, laxius tamen, omnes transversales tantum. Omnes autem transversales componuntur ex duobus terminis lineae rectae; hinc et facillimum prodit artificium data quacunque cognata numerum gradus complecti, v. g. in simplicissima transversalium persona, Fratre seu Patris filio, quia pater est in l, filius etiam in gradu l + l f. 2, in quo est Frater. Caeterum Schemate opus est. Esto igitur hoc:
| Gr. | Cognationes | Datus | Personae | Gr. | ||||||||||
| 1. | Patris | 2 | 4 | Filius | 1. | |||||||||
| Patris | Frater 1.1 |
Filius | ||||||||||||
| 2. | Avi | 3 | 12 | Nepos | 2. | |||||||||
| Patruus 2.1 |
Patruelis 1.2 |
|||||||||||||
| 3. | Proavi | 4 | 32 | Pronepos | 3. | |||||||||
| Patruus Magnus 3.1 |
Consobrinus 2.2 |
Patruelis Parvus 1.3 |
||||||||||||
| 4. | Abavi | 5 | 80 | Abnepos | 4. | |||||||||
| Subpropatruus 4.1 |
Subpropatruus Magnus 3.2 |
Subconsobrino 2.3 |
Propatruelis 1.4 |
|||||||||||
| 5. | Atavi | 6 | 192 | Atnepos | 5. | |||||||||
| Abpatruus 5.1 |
Propatruus 4.1 |
Prosubpatruus Magnus vel Consobrin. secundus 3.3 |
Prosubconsobrinus 2.4 |
Abpatruelis 1.5 |
||||||||||
| 6. | Triavi | 7 | 448 | Trinepos | 6. | |||||||||
zur Übersetzung des Abschnitts
Sunt in hoc schemate infinita propemodum digna observatione. Nos pauca stringemus. Personae eo loco intelligantur, ubi puncta sunt. Numeri puncta includentes designant terminos seu gradus lineae rectae (antecedens ascendentis, sequens descendentis) ex quibus datus gradus transversalis componitur. In eadem linea transversa directa sunt ejusdem gradus cognationes: oblique a summo ad imum dextrorsum ordinem generationis, at sinistrorsum complectuntur cognationes homogeneas gradu differentes. Linea perpendicularis unica a vertice ad basin, triangulum dividens, continet cognationes, quarum terminus et ascendens et descendens sunt ejusdem gradus; tales voco aequilibres, et dantur solum in gradibus pari numero signatis, in uno non nisi unus.
zur Übersetzung des Abschnitts
Nam si libra esse fingatur, cujus trutina sit linea gradus primi, brachia vero sint, dextrum quidem, linea perpendicularis a summa persona descendentium; sinistrum vero, perpendicularis a summa ascendentium ducta ad terminum vel ascendentem vel descendentem datam cognationem componentem; tum brachiis aequalibus, si utrinque 3. 3. aut 2. 2. etc. cognatio erit aequilibris et ponenda in medio trianguli; in inaequalibus, cognatio talis ponenda in eo latere quod lineae rectae vel ascendenti vel descendenti, ex qua brachium longius sumtum est, est vicinum.
zur Übersetzung des Abschnitts
Hic jam complexionum vis apertissime relucet. Componuntur enim omnes personae transversae ex 2 terminis, una cognatione recta ascendenti, altera descendenti semper autem sic, ut ascendens in casu obliquo, descendens in casu recto conjungantur, v. g. frater, id est patris filius. At si contra, redibit persona data, nam qui patrem filii sui nominat, se nominat, quia unus pater plures filios habere potest, non contra.
zur Übersetzung des Abschnitts
Ex his jam datur: proposito quocunque gradu cognationum, tum numerum, tum species reperire; numerus transversalium semper erit unitate minor gradu (numerus omnium semper unitate major, quia addi debent duae cognationes lineae rectae, una sursum, altera deorsum) cujus ratio ex inventione specierum patebit. "Nam com2nationes partium, 𝔬𝔡𝔢𝔯 ℨ𝔢𝔯𝔣𝔞𝔢𝔩𝔩𝔲𝔫𝔤𝔢𝔫 𝔦𝔫 𝔷𝔴𝔢𝔶 𝔗𝔥𝔢𝔦𝔩, dati numeri cujuscunque sunt tot, quot unitates habet numeri dati paris dimidium, imparis demta unitate dimidium, v. g. 6 habet has: 5. 1; 4, 2; 3, 3; ejusque rei ratio manifesta est, quia semper numerus antecedens proximus dato cum remotissimo, paene proximus cum paene remotissimo complicatur etc." Sed cum hic non solum complexionis, sed et situs habenda ratio sit, v. g. alia cognatio est 5.1, nempe Abpatrui, quam 1.5, nempe Abpatruelis, hinc cum 2 res situm varient 2 vicibus. Ergo duplicentur discerptiones, redibit numerus datus si par fuerat; sed cum in ejus discerptionibus detur una, homogenea, v. g. 3.3, in qua nihil dispositio mutat, hinc subtrahatur de numero dato, seu duplo discerptionem, iterum: 1. si vero numerus datus fuerat impar, redibit numerus unitate minor.
zur Übersetzung des Abschnitts
Ex hoc manifestum est generaliter: (1) Subtrahatur de numero gradus unitas, productum erit numerus cognationum transversalium; (2) duo numeri, qui sibi sunt complemento ad datum, seu quorum unus tantum distat ab 1, quantum alter a dato, complicati dabunt Speciem cognationis, si quidem praecedens intelligatur significare ascendentem, sequens descendentem sui gradus. Hac occasione obiter explicandum est, quae sint dati numeri discerptiones, ℨ𝔢𝔯𝔣𝔞𝔢𝔩𝔩𝔲𝔫𝔤𝔢𝔫, possibiles.
zur Übersetzung des Abschnitts
Nam omnes quidem discerptiones sunt complexiones, sed complexionum eae tantum discerptiones sunt, quae simul toti sunt aequales. Instigari similiter possunt tum com2nationes, tum con3nationes, tum discerptiones simpliciter, tum dato exponente. Quot factores vel divisiores exactos numerus aliquis datus habeat, scio solutum vulgo. Et hinc est quod Plato numerum civium voluit esse 5040, quia hic numerus plurimas recipit divisiones civium pro officiorum generibus, nempe 60, lib. 5. de Legib. fol. 845. Et hoc quidem in multiplicatione et divisione, sed qui additione datum numerum producendi varietates, et subtractione discerpendi collegerit, quod utrumque eodem recidit, mihi notus non est. Viam autem colligendi com2nationes discerptionum ostendimus proxime. At ubi plures partes admittuntur ingens panditur abyssus discerptionum, in qua videmur nobis aliquod fundamentum computandi agnoscere, nam semper discerptiones in 3 partes oriuntur ex discerptionibus in 2, praeposita una; exsequi,·vero hujus loci fortasse, temporis autem non est.
zur Übersetzung des Abschnitts
Caeterum antequam in Arbore nostra a computatione generali ad specialem veniamus, unum hoc admonendum est, Definitiones cognationum a nobis assignatas in populari usu non esse. Nam v. g. Patruum nemo definit avi filium, sed potius patris fratrem. Quicunque igitur has definitiones ad popularem efformare morem velit, si quidem persona transversalis ascendit, in termino descendenti loco filii substituat fratrem; nepotis patruum etc. loco Descendentem ponat uno gradu minorem; sin descendit, contra.
zur Übersetzung des Abschnitts
Nunc igitur cum ostendimus cognationes in quolibet gradu, gradus numero unitate majores esse, age et personas cognationum numeremus, quae est Specialis Enumeratio. Diximus autem in eadem cognatione diversitatem facere tum sexum cognatae, tum intermediarum inter cognatam et datam personarum. Sexus autem duplex est. Igitur semper continue numerus personarum est duplicandus, v. g. non solum et pater et mater sexu variant, 2, sed iterum pater habet patrem vel matrem. Et mater quoque; hinc 4. Avus quoque a patre habet patrem vel matrem, et avia a patre, et avus a matre aviaque similiter; hinc 8 etc. Igitur regulam colligo: "2 ducatur toties in se, quotus est gradus cujus personae quaeruntur, vel quod idem est, quaeratur numerus progressionis geometricae duplae, cujus exponens sit numerus gradus. Is ducatur in numerum cognationum dati gradus: productum erit numerus personarum dati gradus."
Et hac methodo eundem numerum personarum erui, quem Paulus JCtus in d. l. 10. excepto gradu 5. Gr. I 2 ᴖ 2 f. 4. consentit Paulus d. 1. l0. §. 12. Gr.II. 2 ᴖ 2 f. 4 ᴖ 3 f. 12, §. 13. Gr. III. 2.2.2 ᴖ f. 8 ᴖ 4 f. 32, §. 14. Gr. IV. 2. 2. 2. 2 ᴖ f. 16 ᴖ 5 f. 80, §. 15. Gr. V. 2. 2. 2. 2. 2 ᴖ f. 32 ᴖ 6 f. 192, dissentit Paulus §. 17. et ponit: 184, cujus tamen calculo errorem inesse necesse est. Gr. VI. 2. 2. 2. 2. 2. 2 ᴖ f. 64 ᴖ 7 f. 447, consentit Paulus §. 17. Gr. VII.2. 2. 2. 2. 2. 2. 2 ᴖ f. 128 ᴖ 8 f. 1024, §. fin. 18.
zur Übersetzung des Abschnitts
Probl. IV.
Dato numero rerum, variationes ordinis inveniere.
| 1 | 1 |
| 2 | 2 |
| 6 | 3 |
| 24 | 4 |
| 120 | 5 |
| 720 | 6 |
| 5040 | 7 |
| 40320 | 8 |
| 362880 | 9 |
| 3628800 | 10 |
| 39916800 | 11 |
| 479001600 | 12 |
| 6227020800 | 13 |
| 87178291200 | 14 |
| 1307874368000 | 15 |
| 20922789888000 | 16 |
| 355687428096000 | 17 |
| 6402373705728000 | 18 |
| 121645100408832000 | 19 |
| 2432902008176640000 | 20 |
| 51090942171709440000 | 21 |
| 1124000727777607680000 | 22 |
| 15852016738884976640000 | 23 |
| 620448401733239439360000 | 24 |
Solutio: Ponantur omnes numeri ab unitate usque ad Numerum rerum, inclusive, in serie naturali: factus ex omnibus continue, erit quaesitum. ut: esto tabula ח quam ad 14. usque continuavimus. Latus dextrum habet exponentes, seu numeros rerum, qui hic coincidunt; in medio sunt ipsae Variationes. Ad sinistrum posita est differentia variationum duarum proximarum, inter quas est posita. Quemadmodum exponens in latere dextro est ratio variationis datae ad antecedentem. Ratio solutionis erit manifesta, si demonstraverimus Exponentis dati variationem esse, factum ex ductu ipsius in variationem exponentis antecedentis, quod est fundamentum Tabulae ח. In hunc finem esto aliud Schema ו. In eo 4 rerum ABCD. 24. variationes ordinis, oculariter expressimus. Puncta significant rem praecedentis lineae directe supra positam. Methodum disponendi secutis sumus, ut primum quam minimum variaretur, donec paulatim omnia. Caeterum quasi limitibus distinximus variationes exponentis antecedentis ab iis quas superaddit sequens. Breviter igitur: Quotiescunque varientur, res datae, v. g. tres 6. 𝔪𝔞𝔥𝔩: addita una praeterea poni poterit servatis variationibus prioris numeri jam initio, jam 2do, jam 3tio, jam ultimo seu 4to loco; seu toties poterit prioribus varie adjungi, quot habet unitates: Et quotiescunque prioribus adjungetur priores variationes omnes ponet. Vel sic quaelibet res aliquem locum tenebit semel, cum interim reliquae habent variationem antecedentem inter se, conf. problem. 7. Patet igitur variationes priores in exponentem sequentem ducendes esse. Theoremata hic observo sequentia: (1.) omnes numeris variationum sunt pares; (2.) omnes vero quorum exponens non est supra 5 in cyphram desinunt, imo in tot cyphras, quoties exponens 5narium continet, (3.) Omnes summae Variationum (id est aggregata variationum ab 1. aliquousque) sunt impares; & desinunt in 3 ab exponente 4 in infinitum. (4.) quaecunque variatio antecedens, ut & exponens ejus omnes sequentes variationes metitur.
| A | b | c d |
| • | • | d c |
| • | c | b d |
| • | • | b d |
| • | d | b c |
| • | • | c b |
| B | a | c d |
| • | • | d c |
| • | c | a d |
| • | • | d a |
| • | d | a c |
| • | • | c a |
| C | b | a d |
| • | • | d a |
| • | a | b d |
| • | • | d b |
| • | d | b a |
| • | • | a b |
| D | b | c a |
| • | • | a c |
| • | c | b a |
| • | • | a b |
| • | a | b c |
| • | • | c b |
(5) Numeri variationum conducunt ad conversione progressioni arithmeticae in harmonicam. Esto enim progressio arithmetica 1. 2. 3. 4. 5. convertenda in harmonicam; Maximi numeri, h. l. 5. quaeratur Variatio: 120. ea dividatur per singulos, prodibunt: 120. 60. 40. 30. 24. termini harmonicae progressionis. Per quos si dividatur idem numerus: 120. numeri progressionis illius arithmeticae redibunt. (6) Si data quaecunque variatio duplicetur, a producto subtrahatur factus ex ductu proxime antecedentis in suum exponentem, residuum erit summa utriusque variationis, v. g. 24ᴖ2 f. 48- 6ᴖ3, 18 f. 30 = 6+24 f. 30. (7) Variatio data ducatur in se, factus dividatur per antecedentem, prodibit differentia inter datam et sequentem, v. g. 6ᴖ6 f. 36. ᴗ 2 f. 18 = 24-6 f. 18. Inprimis autem duo haec postrema theoremata non facile obvia crediderim. Usus etsi multiplex est, nobis tamen danda opera, ne caeteris problematibus omnia praeripiamus. Cumque serias inprimis applicationes Complexionum doctrinae miscuerimus (saepe enim necesse erat ordinis Varietates in Complexiones duci), erunt hic pleraque magis jucunda, quam utilia. Igitur quaerunt, quoties datae quotcunque personae uni mensae alio atque alio ordine accumbere possint. Drexelius in Phaethonte orbis seu de vitiis linguae p. 3. c. l, ubi de lingua otiosa, ita fabulam narrat: Paterfamilias nescio quis 6 ad coenam hospites invitaverat. Hos cum accumbendi tempus esset, προεδρίαν sibi mutuo deferentes, ita increpat: quid? an stantes cibum capiemus? imo ne sic quidem, quia et stantium necessarius ordo est. Nisi desinitis, tum vero ego vos, ne conqueri possitis, toties ad coenam vocabo, quoties variari ordo vester potest. Hic antequam loqueretur, ad calculos profecto non sederat, ita enim comperisset ad 720 variationes (tot enim sunt de 6 exponente, uti Drexelius illic 12 paginis, et in qualibet pagina 3 columnis et in qualibet columna 20 variationibus oculariter monstravit) totidem coenis opus esse; quae etsi continuarentur, 720 dies, id est l0 supra biennium absument. Harsdörfferus Delic. Math. p. 2. sect. l. prop. 32 hospites ponit 7; ita variationes, coenae, dies erunt 5040, id est anui 14 septimanae 10. At Georg. Henischius, Medicus Augustanus, Arithmeticae perfectae lib. 7. pag. 399 hospites vel convictores ponit 12; variationes, coenae, dies prodeunt 479001600; ita absumentur anni 1312333 et dies 5. Imo si quis in hoc exponente tentare vellet, quod Drexelius in dimidio ejus effecit, nempe variationes oculariter experiri, annos insumeret 110, demto quadrante, et si singulis diebus 12 horis laboraret et hora qualibet 1000 variationes effingeret. Pretium operae si Diis placet! Alii, ut cruditatem nudae contemplationis quasi condirent, versus elaborant, qui salvo et sensu et metro et verbis variis modis ordinari possunt. Tales primus Jul. Caes. Scaliger lib. 2. Poetices Proteos appellat. Horum alii minus artis habent, plus variationis, ii nempe quorum omnis est a monosyllabis variatio; alii contra, in quibus temperatura est monosyllaborum caeterorumque. Et quoniam in his plurimae esse solent inutiles variationes, de quibus Problemate 11 et 12 erit contemplandi locus, de illis solis nunc dicemus. Bernhardus Bauhusius, Societatis Jesu, Epigrammatum insignis artifex, tali Hexametro Salvatoris nostri velut titulos μονοσυλλάβους complexus est:
-
Rex, Dux, Sol, Lex, Lux, Fons, Spes, Pax, Mons, Petra
CHRISTUS.
Hunc Eryc. Puteanus Thaumat. Pietat. Y. pag. 107, aliique ajunt variari posse vicibus 362680, scilicet monosyllabas tantum respicientes, quae 9; ego numerum prope decies majorem esse arbitror, nempe hunc 3628800. Nam accedens decima vox CHRISTUS etiam ubique potest poni, dummodo Petra maneat immota, et post petram vel vox Christus vel 2 monosyllaba ponantur. Erunt igitur variationes inutiles, quibus post Petram ponitur 1 monosyllaba proxime antecedente Petram Christo; id contingit quoties caeterae 8 monosyllabae sunt variabiles, nempe 40320 𝔪𝔞𝔥𝔩, cum ultima possit esse quaecunque ex illis, 9. 40320ᴖ9 f. 362880 - 3628800 f. 3265920, qui est numerus utilium versus hujus Bauhusiani variationum. Thomas Lansius vero amplius progressus praefatione Consultationum tale quid molitus est:
- Lex, Rex, Grex, Res, Spes, Jus, Thus, Sal, Sol (bona), Lux, Laus.
- Mars, Mors, Sors, Lis, Vis, Styx, Pus, Nox, Fex (mala), Crux, Fraus.
Hic singuli versus, quia 11 monosyllabis constant, variari possunt vicibus 39916800. Horum exemplo Joh. Philippus Ebelius Giessensis, Scholae Ulmensis quondam Rector, primum hexametrum, deinde elegiacum distichon commentus est. Ille extat praefat. n. 8; hoc, quia et retrocurrit, in ipso opere pag. 2 Versuum Palindromorum, quos in unum fasciculum collectos Ulmae anno 1623 in 12mo edidit. Hexameter ita habet:
- DIs, VIs, LIs, LaUs, fraUs, stirps, frons, Mars, regnat In orbe.
Ubi eadem opera annus quo et compositus est, et verissimus erat, a Christo nato 1620mus, exprimitur. Cujus cum monosyllabae sint 8, 40320 variationes necesse est nasci. At Distichon ad Salvatorem tale est:
- Dux mihi tu, mihi tu Lux, tu Lex, Jesule, tu Rex : Jesule tu Pax, tu Fax mihi, tu mihi Vox.
Variationes ita computabimus: tituli Salvatoris μονοσύλλάβοι sunt 7; hi inter se variantur 5040 vicibus. Cumque singulis adjecta sit vox Tu, quae cum titulo suo variatur 2 vicibus, quia jam ante, jam post poni potest, idque contingat vicibus septem, ducatur 2 narius septies in se, 2. 2. 2. 2. 2. 2ᴖ2 lf. 128 seu Bissurdesolidum de 2, factus ducatur in 5040ᴖ128 f. 645120; productum erit Quaesitum. Hos inter nomen suum, voluit et Joh. Bapt Ricciolus legi, ut alieniori in opere Poetica facultas professoris quondam sui tanto clarius reluceret. Symbola ejus Almagest. nov. P. l. lib. 6. c. 6, Scholio 1, fol. 413 talis:
- Hoc metri tibi eo me nunc hic, Thety, Protea sacro: Sum Stryx, Glis, Grus, Sphynx, Mus, Lynx, Sus, Bos, Caper et Hydrus.
cujus 9 monosyllabae variantur 362880 vicibus. Si loco postremarum vocum: et Hydrus, substituisset monosyllabas, v. g. Lar, Grex, ascendisset ad Lansianas varietates. Hic admonere cogor, ne me quoque contagio criminis corripiat, primam in Thety correptam non legi. Et succurrit opportune Virgilianus ille, Georg. lib. 1. v. 31:
- Teque sibi generum Thetys emat omnibus undis.
Nam alia Thetys, Oceani Regina, Nerei conjux; alia Thetys, nympha marina vilis, Peleo mortali nupta, Achillis parens, nec digna cui te Proteus sacret. Ea sane corripitur:
- Vecta est frenato caerula pisce Thetys.
Caeterum Ricciolus Scaligerum imitari voluit, utriusque enim de Proteo Proteus est. Hujus autem iste:
- Perfide sperasti divos te fallere Proteu.
De cujus variationibus infra probl. fin. Ne vero Germani inferiores viderentur, elaborandum sibi Harsdörfferus esse duxit, cujus Delic. Math. P. 3. sect. 1. prop. 14 distichon extat:
- 𝔈𝔥𝔯, 𝔎𝔲𝔫𝔰𝔱,𝔊𝔢𝔩𝔡, 𝔊𝔲𝔱𝔥, 𝔏𝔬𝔟, 𝔚𝔢𝔦𝔟 𝔲𝔫𝔡 𝔎𝔦𝔫𝔡
- 𝔐𝔞𝔫 𝔥𝔞𝔱, 𝔰𝔲𝔠𝔥𝔱, 𝔣𝔢𝔥𝔩𝔱, 𝔥𝔬𝔣𝔣𝔱 𝔲𝔫𝔡 𝔳𝔢𝔯𝔰𝔠𝔥𝔴𝔦𝔫𝔡.
Cujus 11 monosyllaba habent variationes 39916800. Tantum de versibus. Quanquam autem et Anagrammata huc pertinent, quae nihil sunt aliud, quam variationes utiles literarum datae orationis, nolumus tamen vulgi scrinia compilare. Unum e literaria re vel dissensu computantium quaeri dignum est: quoties situs literarum in alphabeto sit variabilis. Clav. Com. in Sphaer. Joh. de Sacro Bosco cap. 1. pag. 36 [46!]. 23 literarum linguae latinae dicit variationes esse 25852016738884976640000, cui nostra assentitur computatio; 24 literarum Germanicae linguae variationes Laurembergius assignavit 620448397827051993, Erycius Puteanus dicto libello, 62044801733239439360000, at Henricus ab Etten: 620448593438860613360000, omnes justo pauciores. Numerus verus ut in tabula ח manifestum, est hic: 620448401733239439360000. Omnes in eo conveniunt, quod numeri initiales sint 620448. Puteaneae computationis error non mentis, sed calami vel typorum esse videtur, nihil aliud enim, quam loco 7mo numerus 4 est omissus. (Aliud autem sunt variationes, aliud numerus vocum ex datis literis componibilium. Quae enim vox 23 literarum est? Imo quantacunque sit, inveniantur omnes complexiones 23 rerum, in singulas ducantur variationes suae juxta probl. 2 num. 59, productum erit numeros omnium vocum nullam literam repetitam habentium. At habentes reperire docebit problema 6.) Porro tantus hic numerus est, ut, etsi totus globus terraqueus solidus circumquaque esset, et quilibet spatiolo homo insisteret, et quotannis, imo singulis horis morerentur omnes surrogatis novis, summa omnium ab initio mundi ad finem usque multum abfutura sit, ut ait Harsdörff. d. I. Hegiam Olynthium Graecum dudum censuisse. His contemplationibus cum nuper amicus quidam objiceret, ita sequi, ut liber esse possit, in quo omnia scripta scribendaque inveniantur: Tum ego: et fateor, inquam, sed legenti grandi omnino fulcro opus est, ac vereor ne orbem terrarum opprimat. Pulpitum tamen commodius non inveneris cornibus animalis illius, quo Muhamed in coelum vectus arcana rerum exploravit, quorum magnitudinem et distantiam Alcorani oracula dudum tradiderunt. Vocum omnium ex paucis literis orientium exemplo ad declarandam originem rerum ex atomis usus est ex doctrina Democriti ipse Aristot. 1. de Gen. et Corr. text. 5. et illustrius lib. 1. Metaph. c. 4, ubi ait ex Democrito, Atomos differe σχήματι, id est figura, uti literas A et N; ϑέσει, id est situ, uti literas N et Z. si enim a latere aspicias, altera in alteram commutabitur; τάξει, id est ordine, v. g. Syllabae AN et NA. Lucret. quoque lib. 2 ita canit:
- Quin etiam refert nostris in versibus ipsis
- Cum quibus (complexiones} et quali sint ordine (variatio situs) quaeque locata
- Namque eadem coelum, mare, terras, flumina, Solem
- Significant: eadem fruges, arbusta, animantes:
- Si non omnia sint, al multo maxima pars est
- Consimilis; verum positura discrepitant haec.
- Sic ipsis in rebus item jam materiai
- Intervalla, viae, connexus, pondera, plagae,
- Concursus, motus, ordo, positura figura
- Cum permutantur, mutari res quoque debent.
Et Lactant. Divin. Inst. lib. 3· c. 19. pag. m. 163.·Vario, inquit (Epicurus) ordine ac positione conveniant atomi sicut literae, quae cum sint paucas, varie tamen collocatae innumerabilia verba conficiunt. Add. Pet. Gassend. Com. in lib. 10. Laertii ed. Lugduni anno 1649· fol. 227, & Joh. Chrysost. Magnen. Democrit. redivivo Disp. 2. de Atomis c. 4. prop.32. p. 269. Denique ad hanc literarum transpositionem pertinet ludicrum illud docendi genus, cujus meminit Hieronymus ad Paulinam, tesserarum usu literas syllabasque puerulis imprimens. Id Harsdörfferus ita ordinat Delic. Math. P. 2. sect. 13. prop. 3: sunt 6. cubi, quilibet cubus sex laterum est, eruntque inscribenda 36, haec nempe: I. a. e. i. o. u. y. II. b. c. d. f. g. h. III. k. l. m. n. p. q. IV. r. s. ß t. w. x. V. v. j. s. r. ä. ö. VI ff. ss. tz. sch. ch. z. Alphabetum autem lusus unius tesserae, syllabas (𝔡𝔞𝔰 𝔅𝔲𝔠𝔥𝔰𝔱𝔞𝔟𝔦𝔯𝔢𝔫) duarum docebit: inde paulatim voces orientur.
zur Übersetzung des Abschnitts
Probl. V.
Dato numero rerum, variationem situs mere relati seu vicinitas inveniere.
"Quaeratur Variatio situs absoluti, seu ordinis, de numero rerum unitate minori quam est datus, juxta probl. 4, quod invenitur in Tab. ה erit quaesitum." Ratio solutionis manifesta est·in schemate ו quo rationem solutionis problematis praecedentis dabimus, v. g. in variationibus vicinitatis, variationes hae: Abcd. Bcda. Cdab. Dabc. habentur pro una, velut in circulo scripta. Et ita similiter de caeteris; omnes igitur illae 24 variationes dividendae sunt per numerum rerum, qui hoc loco est 4, prodibit variatio ordinis de numero rerum antecedenti, nempe 6. Finge tibi hypocaustum rotundum in omnes 4 plagas januas habens, et in medio positam mensam (quo casu quis sit locus honoratissimos disputat Schwenter, et pro janua orientem spectante decidit, e cujus regione collocandus sit honoratissimus hospes. Delic. Math. sect. VII. prop. 28.) atque ita hospitum situm variari cogita prioritatis posterioritatisque consideratione remota. Hic obiter aliquid de Circulo in demonstratione perfecta dicemus. Ejus cum omnes Propositiones, sint convertibiles, prodibunt syllogismi sex, circuli tres. Ut esto demonstratio: I. O. rationale est docile. O. homo est rationalis. E. O. homo est docilis. II O. homo est docilis. O. rationale est homo. E. O. rationale est docile. 2. III. O. homo est rationalis. O. docile est homo. E. O. docile est rationale. IV. O. docile est rationale. O. homo est docilis. E. O. homo est rationalis. 3. V. O. homo est docilis. O. rationale est homo. E. O. rationale est docile. VI. O. rationale est docile. O. homo est rationalis. E. O. homo est docilis.
zur Übersetzung des Abschnitts
Probl. VI.
Dato numero rerum variandarum, quarum aliqua vel aliquae repetuntur, variationem ordinis inveniere.
"Numerentur res simplices et ex iisdem repetitis semper una tantum, et ducantur in variationem numeri numero variationum dato unitate minoris; productum erit quaesitum." V. g. sint sex: a. b. c. c. d. e, sunt simplices 4 + l (duo illa c habentur pro 1) f. 5 ᴖ 120 (120 autem sunt variatio numeri 5 a antecedentis datum 6) f. 600. Ratio manifesta est, si quis intueatur schema וּ; corruent enim omnes variationes, quibus data res pro se ipsa ponitur. Usum nunc monstrabimus. Esto propositum: dato textu omnes melodias possibiles invenire. Id Harsdörfferus quoque Delic. Math. sect. 4. prop. 7. tentavit. Sed ille in textu 5 syllabarum melodias possibiles non nisi 120 esse putat, solas variationes ordinis intuitus. At nobis necessarium videtur etiam complexiones adhibere, ut nunc apparebit. Sed altius ordiemur: Textus est vel simplex, vel compositus. Compositum voco in lineas, ℜ𝔢𝔦𝔪𝔷𝔢𝔦𝔩𝔢𝔫, distinctum. Et compositi textus variationem discemus melodiis simplicium in se continue ductis per probl. 3. Textus simplex vel excedit 6 syllabas, vel non excedit. Ea differentia propterea necessaria est, quia 6 sunt voces: Ut, Re, Mi, Fa, Sol, La (ut omittam 7mam: Bi, quam addidit Eryc. Puteanus in Musathena). Si non 6 excedit, aut sex syllabarum, aut minor est. Nos in exemplum de Textu hexasyllabico ratiocinabimur, poterit harum rerum intelligens idem in quocunque praestare. Caeterum in omnibus plusquam hexasyllabicis necesse est vocum repetitionem esse. Porro in textu hexasyllabico capita variationum sunt haec:
| I. | ut re mi fa sol la Variatio ordinis est | 720 |
| II. | ut ut re mi fa sol, Variatio ordinis est 720-120 f. 600. Non solum autem ut, sed et quaelibet 6 vocum potest repeti 2 𝔪𝔞𝔥𝔩, ergo 6 ᴖ 600 f. 3600; et reliquarum 5 vocum semper 5 𝔪𝔞𝔥𝔩, aliae 4 possunt poni post ut ut, nempe: re, mi, fa, sol. re, mi, fa, la. re, mi, sol, la. re, fa, sol, la. mi, fa, sol, la; seu 5 res habent 5 con4nationes: 5 ᴖ 3600 f. | 18000 |
| III. | ut ut re re mi fa, 480 ᴖ 15 f. 7200 ᴖ 6 f. | 43200 |
| IV. | ut ut re re mi mi, 360 ᴖ 20 f. | 7200 |
| V. | ut ut ut re mi fa, 360 ᴖ 6 f. 2160 ᴖ 20 r. | 43200 |
| VI. | ut ut ut re re mi, 360 ᴖ 6 ᴖ 5 ᴖ 4 r | 43200 |
| VII. | ut ut ut re re re, 240 ᴖ 15 f. | 3600 |
| VIII. | ut ut ut ut re mi, 360 ᴖ 6 ᴖ 10 f. | 21600 |
| IX. | ut ut ut ut re re, 240 ᴖ 6 ᴖ 5 f. | 7200 |
| Summa | 187920 | |
Quid vero si septimam vocem Puteani Bi, si pausas, si inaequali talem celeritatis in notis, si alios characteres musicos adhibeamus computationi, si ad textus plurium syllabarum quam 6, si ad compositos progrediamur, quantum erit mare melodiarum, quarum pleraeque aliquo casu utiles esse possint? Admonet nos vicinitas rerum, posse cujuslibet generis carminum possibiles species seu flexus, et quasi Melodias inveniri, quae nescio an cuiquam hactenus vel tentare in mentem venerit. Age in Hexametro conemur. Cum hexametro sex sint pedes, in caeteris quidem dactylus spondaeusque promiscue habitare possunt, at penultimus non nisi dactylo, ultimus spondaeo aut trochaeo gaudet. Quod igitur 4 priores attinet, erunt vel meri dactyli: l, vel meri spondaei: l, vel tres dactyli, unus spondaeus, vel contra: 2, vel 2 dactyli, 2 spondaei: 1, et ubique variatio situs 12, 2 + l f. 3 ᴖ 12 f. 36 + l + l f. 38. In singulis autem his generibus ultimus versus vel spondaeus vel trochaeus est, 2 ᴖ 38 f. 76. Tot sunt genera hexametri, si tantum metrum species. Ut taceam varietates, quae ex vocibus veniunt, v. g. quod vel ex monosyllabis vel dissyllabis etc. vel his inter se mixtis constat; quod vox modo cum pede finitur, modo facit caesuram eamque varii generis; quod crebrae intercedunt elisiones aut aliquae aut nullae. Caeterum et multitudine literarum hexametri differunt, quam in rem exstat carmen Publilii Porphyrii Optatiani (quem male cum Porphyrio Graeco, philosopho, Christianorum hoste, Caesar Baronius confudit) ad Constantinum Magnum, 26 versibus heroicis constans, quorum primus est 25 literarum, caeteri continue una litera crescunt, usque ad 26tum qui habet 50; ita omnes organi Musici speciem exprimunt. Meminere Hieron. ad Paulinam, Firmicus in Myth., Rab. Maurus, Beda de re metrica. Edidit Velserus ex Bibliotheca sua Augustae cum figuris An. 159l. Adde de eo Eryc. Puteanum in Thaum. Pietatis lit. N, qui ait hoc carmine revocari ab exilio meruisse; Gerh. Joh. Vossium syntag. de Poet. Latinis v. Optatianus; item de Historicis Graecis, 1. 16. Casp. Barthium Commentariolo de Latina Lingua, et Aug. Buchnerum Notis in Hymnum Venatii Fortunati (qui vulgo Lactantio ascribitur) de Resurrect. ad v. 29. pag. 27, qui observat Hexametros fistulis, versum per medium auctum: Augusto victore etc. regulae organi, jambos anacreonticos dimetros omnes 18 literarum, epitoniis respondere. Versus ipsos, quia ubique obvii non sunt, expressimus:
| 25 | O si diviso Metiri Limite Clio |
| 26 | Una Lege Sui Uno Manantia Fonte |
| 27 | Aonio Versus Heroi Jure Manente |
| 28 | Ausuro Donet Metri Felicia Texta |
| 29 | Augeri Longo Patiens Exordia Fine |
| 30 | Exiguo Cursu Parvo Crescentia Motu |
| 31 | Ultima Postremo Donec Vestigia Tota |
| 32 | Ascensus Jugi Cumulato Limite Cludat |
| 33 | Uno Bis Spatio Versus Elementa Prioris |
| 34 | Dinumerans Cogens Aequali Lege Retenta |
| 35 | Parva Nimis Logis Et Visu Dissona Multum |
| 36 | Tempore Sub Parili Metri Rationibus Isdem |
| 37 | Dimidium Numero Musis Tamen Aequiparantem |
| 38 | Haec Erit In Varios Species Aptissima Cantus |
| 39 | Perque Modos Gradibus Surget Fecunda Sonoris |
| 40 | Aere Caro Et Tereti Calamis Crescentibus Aucta |
| 41 | Quis Bene Suppositis Quadratis Ordine Plectris |
| 42 | Artificis Manus Innumeros Clauditque Aperitque |
| 43 | Spiramenta Probans Placitis Bene Consona Rythmis |
| 44 | Sub Quibus Unda Latens Properantibus Incita Ventis |
| 45 | Quas Vicibus Crebris Iuvenum Labor Haud Sibi Discors |
| 46 | Hinc Atque Hinc Animaeque Agitant Augetque Reluctans |
| 47 | Compositum Ad Numeros Propriumque Ad Carmina Praestat |
| 48 | Quodque Queat Minimum Admotum Intremefacta Frequenter |
| 48 | Plectra Adaperta Sequi Aut Placitos Bene Claudere Cantus |
| 50 | Jamque Metro Et Rythmis Praestringere Quicquid Ubique Est. |
| 25 | Post martios labores, | 38 | Feruntque dona laeti. |
| 26 | Et Caesarum parentes | 38 | Jam Roma culmen orbis |
| 27 | Virtutibus, per orbem | 40 | Dat munera et coronas |
| 28 | Tot laureas virentes, | 41 | Auro ferens coruscas |
| 29 | Et Principis trophaea; | 42 | Victorias triumphis, |
| 30 | Felicibus triumphis | 43 | Votaque jam theatris |
| 31 | Exultat omnis aetas, | 44 | Redduntur et Choreis. |
| 32 | Urbesque flore grato | 45 | Me sors iniqua laetis |
| 33 | Et frondibus decoris | 46 | Solemnibus remotum |
| 34 | Totis virent plateis. | 47 | Vix haec sonare sivit |
| 35 | Hinc ordo veste clara | 48 | Tot vota fronte Phoebi |
| 36 | In purpuris honorum | 49 | Versuque comta sola, |
| 37 | Fausto precantur ore, | 50 | Augusta rite seclis. |
Ex quibus multa circa scripturam Veterum observari possunt, inprimis Diphthongum Æ duabus literis exprimi solitam; qui tamen mos non est, cur rationem vincat, unius enim soni una litera esse debet. Sed de hoc Optatiano vel propterea fusius diximus, ut infra dicenda praeoccuparemus, ubi versus Proteos ab eo compositos allegabimus.
zur Übersetzung des Abschnitts
Probl. VII.
Dato capite, variationes reperire.
Hoc in Complexionibus solvimus supra. De situs variationibus nunc: Sunt autem diversi casus. Caput enim Variationis hujus aut constat una re, aut pluribus: si una, ea vel monadica est, vel dantur inter Res (variandas) alia aut alia: ipsi homogeneae. Sin pluribus constat, tum vel intra caput dantur invicem homogeneae vel non, item extrinsece quaedam intrinsecis homogeneae sunt vel non.
Primum igitur capite variationis fixo manente numerentur, res extrinsecae; & quaeratur variatio earum inter se (& si sint discontiguae seu caput inter eas ponatur) praeciso capite, per prob. 4. productum vocetur A. Si caput multiplicabile non est, seu neque pluribus rebus constat, & una ejus res non habet homogeneam, productum A erit quaesitum.
Sin caput est multiplicabile, & constat 1. re habente homogeneam, productum A multiplicetur numero homogenearum aeque in illo capite ponibilium, & factus erit quaesitum.
Si vero caput constat pluribus rebus quaeratur variatio earum inter se, (etsi sint discontiguae seu res extrinsecae interponantur) per probl. 4. ea ducatur in productum A, quodque ita producitur dicemus B. Jam si res capitis nullam habet homogeneam extra caput, productum B erit quaesitum. Si res capitis habet homogeneam tantum extra caput, non vero intra, productum B. multiplicetur numero rerum homogeneam, & si saepius sunt homogeneae, factus ex numero homogenearum priorum multiplicetur numero homogenearum posteriorum continue, & factus erit quaesitum.
Sin res capitis habet homogeneam intra caput & extra, numerentur primo res homogeneae intrinsecae & extrinsecae simul, & supponantur pro Numero complicando; deinde res datae homogeneae tantum intra caput supponantur pro exponente. Dato igitur numero & exponente quaeratur complexio per probl. I. & si saepius contingat homogeneitas, ducantur complexiones in se invicem continue. Complexio vel factus ex complexionibus ducatur in productum B. Et factus erit quaesitum.
Hoc problema casuum multitudo operosissimum efficit, ejusque nobis solutio multo & labore & tempore constitit. Sed aliter sequentia problemata ex artis principiis nemo solvet. In illis igitur usus hujus apparebit.
zur Übersetzung des Abschnitts
Probl. VIII.
Variationes alteri dato capiti communes reperire.
Utrumque caput ponatur in eandem Variationem quasi esset unum caput compositum (etsi interdum res capitis compositi sint discontiguae) & indagentur variationes unius capitis compositi per probl. 10. productum erit quaesitum.
zur Übersetzung des Abschnitts
Probl. IX.
Capita variationes communes habentia reperire.
Si plura capita in variatione ordinis in eundem locum incidunt vel ex toto vel ex parte, non habent varationes communes. 2. Si eadem res monadica in plura capita incidit, ea non habent variationes communes. Caetera omnia habent variationes communes.
zur Übersetzung des Abschnitts
Probl. X.
Capita variationum utilium aut inutilium reperire.
Capita in universum reperire expeditum est. Nam quaelibet res per se, aut in quocunque loco per se, aut cum quacunque, alia aliisve, quocunque item loco cum alia aliisve, breviter, omnis complexio aut variatio proposita minor & earundem rerum, seu quae tota in altera continetur est caput. Methodus autem in disponendis capitibus utilis, ut a minoribus ad m jota progrediamur, quando v. g. propositum nobis est omnes variationes oculariter proponere, quod Drexelius loco citato Puteanus & Kleppisius & Reimerus citandis factitarunt.
Caeterum ut capita utilia vel inutilia reperiantur, adhibenda disciplina est ad quam res variandae, aut totum ex iis compositum pertinet. Regulae ejus inutilia quidem elident, utilia vero relinquent. Ibi videndum quae cum quibus & quo loco conjungi non possint, item quae simpliciter quo loco poni non possint v. g. primo, tertio, &c Inprimis autem primo & ultimo. Deinde videndum quae res potissimum causa sit anomaliae (v. g. in versibus hexametris proteis syllabae breves) Ea ducenda est per omne caeteras, omnia item loca, si quando autem de pluribus idem judicium est, satis erit in uno tentasse.
zur Übersetzung des Abschnitts
Probl. XI.
Variationes inutiles reperire.
Duae sunt viae (1.) per probl. 12. hoc modo: inventae summa variationum utilium & inutilium per probl. 4.·subtrahatur summa utilium per probl. 12. viam secundam; Residuum erit quaesitum (2.) absolute hoc modo: Inveniantur capita variationum inutilium per probl. 10. quaerantur singulorum capitum variationes per probl. 7. si qua capita communes habent variationes per probl. 9. numerus earum inveniatur per probl. 8. & in uno solum capitum variationes Communes habentium relinquatur, de caeterorum variationibus subtrahatur; aut si hunc laborem subtrahendi subterfugere velis, initio statim capita quam maxime composita pone, conf. probl. 8. Aggregatum omnium variationum de omnibus complexionibus, subtractis subtrahendis, erit quaesitum.
zur Übersetzung des Abschnitts
Probl. XII.
Variationes utiles reperire.
Solutio est ut in proxime antecedenti, si haec saltem mutes, in via 1. loco problem. 12. pone 11. &c. & subtrahatur summa inutilium per probl. 11. viam secundam. In via 2. inveniantur capita variationum utilium? caetera ut in probl. proximo.
zur Übersetzung des Abschnitts
Usus Problem. 7. 8. 9. 10. 11. 12.
Si cui haec problemata aut obvia aut inutilia videntur, cum ad praxin superiorum descenderit aliud dicet. Rarissime enim vel natura rerum vel decus patitur omnes variationes possibiles, utiles esse. Cujus specimen in argumento minus fortasse fructuose, in exemplum tamen maxime illustri daturi sumus.
zur Übersetzung des Abschnitts
Diximus supra Proteos versus esse pure proteos, id est in quibus pleraeque variationes possibiles utiles sunt, ii nimirum qui toti propemodum monosyllabis constant; vel mixtos, in quibus plurimae incidunt inutiles, quales sunt qui polysyllaba, eaque, brevia continet.
zur Übersetzung des Abschnitts
In hoc genere inter veteres, qui mihi notus sit tentavit tale quiddam idem ille de quo probl. 6. Publilius Porphyrius Optatianus. Et Erycius Puteanus Thaumat Piet. lit. N. pag. 92. ex aliis ejus de Constantino versibus hos refert:
- Quem divus genuit Constantius Induperator
- Aurea Romanis propagans secula nato.
Ex illis primus est Torpalius, vocibus continue syllaba crescentibus constans; alter est Proteus sexiformis si ita loqui fas est:
- Aurea Romanis propagans secula nato
- Aurea propagans Romanis secula nato
- Secula Romanis propagans aurea nato
- Secula propagans Romanis aurea nato
- Propagans Romanis aurea secula nato
- Romanis propagans aurea secula nato.
zur Übersetzung des Abschnitts
Verum plures habet primus ille Virgilianus:
- Tityre tu patulae recubans sub tegmine fagi,
quem usus propemodum in jocum vertit. Ejus variationes sunt hae: pro tu sub 2. pro patulae recubans 2. & Tityre jam initio, ut nunc, jam tegmine initio: jam Tityre tegmine fine, jam tegmine Tityre, fine, 4ᴖ2ᴖ2 f. 16. Verum in Porphyrianaeis non singuli Protei, sed omnes, neque unus versus sed carmen totum talibus plenum admirandum est. Ejusmodi versus composituro danda opera, ut voces consonis aut incipiant, aut finiant.
zur Übersetzung des Abschnitts
Alter qui & nomen Protei indicit, est Jul. Caes. Scaliger vir si ingenii ferocia absit, plane incomparabilis, Poet. lib 2 c.30, pag. 185 is hunc composuit, formarum, ut ipse dicit, innumerabilium, ut nos 64.:
- Perfide sperasti divos te fallere Proteu.
Plures non esse facile inveniet, qui vestigia hujus nostrae computationis leget. Pro Perfide fallere 2. pro Proteus divos 2ᴖ2 f. 4. Sperasti divos te, habet variationes 6ᴖ4 f. 24. Divos perfide Te sperasti, habet Var. 2. Divos Te sperasti perfide, habet 6+2+2 f. 10ᴖ4 f. 49+24 f. 64. Observavimus ex Virgilio, aeque, imo plus variabilem, Aen. lib.1.v.282. Queis (pro: His) ego nec metas rerum nec tempora pona [pono]. Nam perfide una vox est; queis ego in duas discerpi potest.
zur Übersetzung des Abschnitts
Venio ad ingeniosum illum Bernhardii Bauhusii Jesuitae Lovaniensis, qui inter Epigrammata ejus extat; utque superior, v. probl. 4·de Christo, ita hic de Maria est:
- Tot tibi sunt dotes virgo, quot sidera coelo.
Dignum hunc peculiari opera esse duxit vir doctissimus Erycius Puteanus libello, quem Thaumata Pietatis inscribit; edito Antverpiae anno 1617. forma 4ta ejusque variationes utiles omnes enumerat a pag. 3. usque ad 50. inclusive quas autore, etsi longius porrigantur, intra cancellos numeri 1022. continuit, tum quod totidem vulgo stellas numerant Astronomi, ipsius autem institutum est ostendere dotes non esse pauciores quam stellae sunt; tum quod nimia propemodum cura omnes illos evitavit, qui dicere videntur, tot sidera coelo, quot Mariae dotes esse, nam Mariae dotes esse multo plures. Eas igitur variationes si assumsisset (v. g. Quot tibi sunt dotes virgo, tot sidera coelo) totidem, nempe 1022. Alios versus ponendo tot pro quot, & contra, emersuros fuisse manifestum est. Hoc vero etiam in praefatione Puteanus annotat pag. 12. interdum non sidera tantum, sed & dotes coelo adhaerere, ut coelestes esse intelligamus, v. g.
- Tot tibi sunt coelo dotes, quot sidera virgo.
Praeterea ad variationem multum facit, quod ultimae in Virgo, & Tibi ambigui quasi census & corripi & produci patiuntur, quod artificium quoque infra in Daumiano illo singulari observabimus.
zur Übersetzung des Abschnitts
Meminit porro Thaumatum suorum & Protei Bauhusiani aliquoties Puteanus in apparatus Epistolarum cent. I. ep. 49·& 57. ad Gisbertum Bauhusium Bernardii Patrem; add. & ep. 51. 52. 53. 56. ibid. Editionem autem harum Epistolarum habeo in 12. Amstelodami anno 1647. nam in editione epistolarum in 4to quia jam anno 1612. prodiit, frustra quaeres.
zur Übersetzung des Abschnitts
Caeterum Joh. Bapt. Ricciol. Almag. nov. P. I. lib. 6. c. 6. schol. 1. f. 413. peccato μνημονικῷ Versus Bauhusiani Puteanum autorem praedicavit his verbis: quoniam vero vetus erat opinio a Ptolemao usque propagata, stellas omnes esse 1022. Erycius Puteanus pietatis & ingenii sui monumentum posterus reliquit, illo artificiosissimo carmine, Tot Tibi, &c qui tamen non autor sed commentator, commendatorque est.
zur Übersetzung des Abschnitts
Denique similem prorsus versum in Ovidio, levissima mutatione observavimus hunc, Metam. XII. fab. 7 v. 594:
- Det mihi se, faxo triplici quid cuspide possim
- Sentiat &c.
Is talis fiet:
- Dant mihi se faxo trina quid cuspide possim.
zur Übersetzung des Abschnitts
Nam etiam ultima in mihi et faxo anceps est. Exstat in eodem genere Georg. Kleppisii, nostratis Poetae laureati, versus hic:
- Dant tria jam Dresdae, ceu sol dat, lumina lucem,
cujus variationes peculiari libro enumeravit 1617; occasionem dedere tres soles, qui anno 1617 in coelo fulsere, quo tempore Dresdae convenerant tres soles terrestres ex Austriaca domo: Matthias Imperator, Ferdinandus Rex Bohemiae, et Maximilianus Archidux, supremus ordinis Teutonici Magister. Libellum illis dedicatum titulo Protei Poetici eodem anno edidit, quem variationum numerus signat.
zur Übersetzung des Abschnitts
Omnino vero plures sunt variationes quam 1617, quod ipse tacite confitetur autor, dum in fine inter Errata ita se praemunit: fieri potuisse, ut in tanta multitudine aliquem bis posuerit, supplendis igitur lacunis novos aliquot ponit quos certus sit nondum habuisse. Nos ut aliquam praxin proximorum problematum exhibeamus, variationes omnes utiles computabimus. Id sic fiet, si inveniemus omnes inutiles. Capita variationum expressimus notis quantitatis, sic tamen ut pro pluribus transpositis unum assumserimus, v. g. — — . — . — . ◡ ◡ . etiam continet hoc: — . — — . — . ◡ ◡ etc. Punctis designamus et includimus unam vocem.
zur Übersetzung des Abschnitts
| Summa omnium variationum utilium et inutilium: | 362880 | |
| 1. | ◡ ◡ . v.g. dant jam Dresdae ceu sol dat lumina lucem | 40320 |
| 2. | — — . ◡ ◡ . Dresdae tria dant jam ceu sol etc. | 10080 |
| 3. | — . — . ◡◡ . dant jam tria. | 14400 |
| 4. | — — . — . — . ◡◡ . Dresdae dant jam tria. | 28800 |
| 5. | — — . — — . ◡◡ . Dresdae lucem tria. | 1440 |
| 6. | — . — . — . — . ◡◡ . dant jam ceu sol tria. | 2880 |
| 7. | — — . — — . — . — . ◡◡ . Dresdae lucem ceu sol tria. | 28800 |
| 8. | — — . — . — . — . — . —◡ . Dresdae dant jam ceu sol tria. | 7200 |
| 9. | — — . — — . — . — . — . ◡◡ . Dresdae lucem dant jam ceu sol tria. | 7200 |
| 10. | in fine ◡◡ . v. g. tria | 40320 |
| Summa variationum ob vocem Tria inutilium, quae exacte constituit dimidium summae variationum possibilium. |
181440 | |
| 11. | ab initio: — . —◡◡ . dant lumina. | 18000 |
| 12. | — . — — . —◡◡ . dant Dresdae lumina. | 9600 |
| 13. | — . — . — . —◡◡ . dant jam ceu lumina. | 4320 |
| 14. | — . — . — . — . — . —◡◡ . dant jam ceu dat lumina. | 240 |
| 15. | — . — — . — — . —◡◡ . dant Dresdae lucem lumina. | 2160 |
| 16. | — . — . — . — — . —◡◡ . dant jam ceu lucem lumina. | 5760 |
| 17. | — . — . — . — . — . — — . —◡◡ . dant ceu jam sol dat lucem lumina. | 0 |
| 18. | — . — . — . — — . — — . —◡◡ . dant ceu jam Dresdae lucem lumina. | 1200 |
| 19. | — . — . — . — . — . — — . — — . ◡◡ . dant ceu jam sol dat lucem Dresdae lumina. | 0 |
| 20. | fine —◡◡ . v. g. lumina | 11620 |
| Summa variationum ob solam vocem Lumina inutilium | 52900 | |
| 21. | ubicunque: —◡◡ . ◡◡ . lumina tria | 40320 |
| 22. | —◡◡ . —◡◡ . lumina Dresdae tria | 14440 |
| 23. | —◡◡ . — . — . —◡◡ . lumina ceu jam tria | 4800 |
| 24. | —◡◡ . — . — . — . — . ◡◡ . lumina ceu jam sol dat tria | 1440 |
| 25. | class="latein"—◡◡ . — — . — — . ◡◡ . lumina Dresdae lucem tria | 480 |
| 26. | —◡◡ . — . — . — — . ◡◡ . lumina ceu jam Dresdae tria | 4800 |
| 27. | —◡◡ . — . — . — — . — — . ◡◡ . lumina ceu jam Dresdae lucem tria | 4080 |
| 28. | —◡◡ . — . — . — . — . — — . ◡◡ . lumina ceu jam dat sol lucem Dresdae tria | 532 |
| 29. | —◡◡ . — . — . — . — . — — . ◡◡ . lumina ceu jam dat sol lucem Dresdae tria | 2978 |
| Summa variationum inut. ob complicationem 28 Lumina et Tria, illo praeposito. |
59870 | |
| 30. | — . ◡◡ . — . — . ◡◡ . dant tria jam lumina. | 2400 |
| 31. | — . ◡◡ . — . — — . — . ◡◡ . dant tria jam Dresdae lumina. | 3840 |
| 32. | — . ◡◡ . — . — . — . —◡◡ . ceu sol | 1440 |
| 33. | — . ◡◡ . — . — . — . — — . —◡◡ . dant tria jam ceu sol lucem lumina. | 5760 |
| 34. | — . ◡◡ . — . — . — . — — . — — . —◡◡ . dant tria jam ceu sol lucem Dresdae lumina | 9360 |
| Summa variationum inut. ob complic. Tria et Lumina, illo praeposito | 22800 59870 52900 181440 |
|
| Summa summarum Var. inut. | 317010 | |
| subtrahatur de summa universali | 362880 | |
| Remanet: | ||
| Summa utilium variationum versus Kleppisii admissis spondaicis | 45870 | |
| Spondaicos reliquimus ne laborem computandi augeremus, quot tamen inter omnes variationes utiles et inutiles existant spondaici, sic invenio. | ||
| 1. | si in fine ponitur — . — — . v.g. dant lucem | 100800 |
| 2. | — — . — — . v. g. Dresdae lucem | 10080 |
| 3. | — . — . — . v. g. dant seu sol | 43300 |
| Summa omnium spondaicorum util. et inut. | 154080 | |
zur Übersetzung des Abschnitts
Extat praeterea versus nobilissimi herois Caroli a Goldstein.
Ars non est tales bene structos scribere versus,
in arte sibi neganda artificiosus, qui 1644 variationes continere dicitur. Aemulatione horum, Kleppisii inprimis, prodiit Henr. Reimerus Lüneburgensis, Scholae patriae ad D. Johannis Collega, Proteo instructus tali:
Da pIe ChrIste UrbI bona paX sIt teMpore nostro.
qui idem annum 1619, quo omnes ejus variationes uno libello in 12. Hamburgi edito inclusi prodierunt, continet.
zur Übersetzung des Abschnitts
Laboriosissimus quoque Daumius, vir in omni genere poematum exercitatus, nec hoc quidem intentatum voluit a se relinquit. Nihil de ejus copia dicam, qua idem termillies aliter carmine dixit (hic enim non alia verba, sed eorundem verborum alius ordo esse debet) quod in hac sententia: fiat justitia aut pereat mundus, Vertumno poetico Cygneae anno 1646. 8. edito praestitit. Hoc saltem adverto, quod et autori annotatum in Millenario 1. num. 219 et 220 versus Proteos esse. Hi sunt igitur:
- v. 219. Aut absint vis, fraus, ac jus ades, aut cadat aether.
- v. 220. Vis, fraus, lis absint, aequum gerat, aut ruat orbis .
zur Übersetzung des Abschnitts
Nacti vero nuper sumus, ipso communicante, alium ejus versum invento sane publice legi digno, quem merito plus quam Protea dicas, neque enim in idem tantum, sed alia plurima carminis genera convertitur. Verba enim haec: O alme (sc. Deus) mactus Petrus (sponsus) sit lucro duplo: varie transposita dant Alcaicos 8. Phaleucios 8. sapphicos 14. Archilochios 42. in quibus omnibus intercedit elisio. At vero sine elisione facit pentametros 32. Jambicos senarios tantum, 20. Scazontes tantum, 22. Scazontes & Jambos simul 44. (& ita Jambos omnes 64. Scazontes omnes 66.) si syllabam addas sit Hexameter, v. g.
Fac duplo Petrus lucro sit mactus, o alme!
variabilis versibus 480.
zur Übersetzung des Abschnitts
Caeterum artificii magna pars in eo consistit, quod plurimae syllabae, ut prima in duplo, petrus, lucro, sunt ancipites. Elisio autem efficit ut eadem verba, diversa genera carminis syllabis se excedentia, efficiant. Alium jam ante anno 1655. dederat, sed variationum partiorem, nempe Alcaicum hunc:
Faustum alma sponsis da Trias o torum!
convertibilem in Phaleucios 4. Sapphicos 5. Pentametros 8. Archilochios 8. Jambicos senarios 14. Scazontes 16.
zur Übersetzung des Abschnitts
Sed jam tempus equum spumantia solvere colla.
Si quis tamen prolixitatem nostram damnat, is vereor; ne cum ad praxin ventum erit, idem versa fortuna de brevitate conqueratur.
zur Übersetzung des Abschnitts
zur Übersetzung des Abschnitts
Finis.
Erörterung über die Wissenschaft der Kombinatorik.
In der auf der Grundlage der Arithmetik das Lehrgebäuder der Verwicklungen und Umstellungen durch neue Vorschriften errichtet wird und der Gebrauch beider durch den Erdkreis der Wissenschaften dargestellt wird; auch werden neue Samen der Kunst zu denken, oder der logischen Erfindung gesäht.
Vorausgeschickt ist eine Zusammenfassung der Abhandlung, und in einem Anhang der Beweis für die Existenz Gottes, zur mathematischen Gewissheit ausgeführt.
Vom Autor Gottfried Wilhelm Leibniz
Magister der Philosophie in Leipzig und Bakkalaurat beider Rechte.
Dem höchsten,großartigen, höchst zu bewundernden Herrn Martin Geier,
geweihter Doktor der heiligen Theologie, obersten Hofprediger des durchlauchtigsten Kurfürsten Sachsens; Beisitzer des obersten Dresdener Kabinetts, und kirchlicher Berater.
Dem unvergleichlichen Theologen:
seinem wahrhaften Förderer und größten Mäzen, über die empfangenen Wohltaten hinaus, Rechenschaft seiner Studien festzustellen,
hat der Autor gewollt.
Zusammenfassung der Erörterung zur Kombinatorik
Die Grundlage dieser Lehre der Arithmetik. Deren Ursprung. Schlussfolgerungen aber gehören zur reinen Arithmetik, gebildet nach der Regel. Die Erläuterung neuer Begriffe. Was wir anderen verdanken. Fragestellung I. Die Schlussfolgerungen aus gegebener Anzahl und Exponent und in der Gattung die Verbindungen zu finden. Fragestellung II. Die Schlussfolgerungen aus der gegebenen Anzahl einfacher zu finden. Deren Gebrauch (1.) in der Trennung von zu findenden Arten: z. B. der Befehle, Elemente, Zahlen, Orgelregister, der unbedingten Regeln des Syllogismus, von denen es auf der Welt nach Johannes Hospinianus 512 gibt, 88 brauchbare nach uns. Neue Arten der syllogistischen Figuren nach Johannes Hospinianus: Barbari, Celaro, Camestros, und unsere. Die 4 Figuren des Galenos von Pergamon: Fresismo, Ditabis, Celanto, Colanto. Johann Christoph Sturm's neue Regeln aus unbegrenzten Begriffen, Daropti. Darstellung der Umwandlungen. Über die Vervielfältigung der Figuren in der Geometrie, durch übereinstimmende, auseinanderstrebende, zusammenzufügende. Die Kunst einen Rechtsfall zu formulieren. Aber die Theologie ist gleichsam eine Art Rechtswissenschaft; über das öffentliche Recht nämlich im Gottesstaat über die Menschen. (2.) zum Auffinden untergeordneter Arten zu den gegebenen Gattungen, die Brauchbarkeit der Untersuchungsregel durch gegebene Teilung. (3.) Der Gebrauch von Hauptsätzen und Beweismittel beim Finden. Die Kombinatorik des Ramon Llull, Athanasius Kircher, unserer, darüber im Folgenden: Es gibt zwei Wortverbindungen in den Hauptsätzen: tatsächlich und nein, oder + und -. Die Bildung von Kategorien in der Kombinatorik. Aufzufinden: von gegebener Festlegung oder Begriff; Begriffsbestimmungen oder gleichbedeutende Begriffe: von einem gegebenen Subjekt erklärt er im Hauptsatz HA, ebenso PA, ebenso N. Die Klassen der Zahlen, Anzahl der Begriffe in den Klassen: die Aussagen von einem gegebenen Subjekt im Hauptsatz UA, PA und N. Von zwei gegebenen Begriffen im notwendigen Hauptsatz UA und UN den seienden Gegenstand oder die mittleren Begriffe zu finden. Über die Stellung des Themas, oder das Verfahren die anschließenden Hauptsätze zu erzeugen und zu prüfen. Wunderbare Beispiele der Kategorien der Kombinatorik. Den Folgesatz über eine allgemeine Schrift eines jeglichen von jedermann zu lesen; der die Sprache kundig versteht, des Abts Alexandre de Cossé-Brissac Beispiel der Kombinatorik oder über die Kriegskunst nachzudenken, zu wessen auch immer Vorteil kommen durch Überlegung alle würdigen Herrscher in den Sinn. Über den Gebrauch konzentrischer Pappscheiben bei dieser Tätigkeit. Die Riegel dieser kunstvoll konstruierten Kombinationsschlösser, die ohne Schlüssel zu öffnen sind / Farbmischungen. Fragestellung III. Von der gegebenen Anzahl Klassen und einzelner Dinge, die Verknüpfungen der Klassen finden. Die Teilung in der Aufteilung zu ziehen, von der gewöhnlichen Teilung des Verständnisses. Die Anzahl der Denkweisen aus dem höchsten Guten aus Publius Terentius Varro bei Augustinus von Hippo. Dessen Überprüfung. Im gegebenen Gard der Blutsverwandtschaft die Anzahl (1.) die Verwandtschaftsverbindung in der Stellung 1. und 3. Grades und die Zuneigung, (2.) die Stellung der Verbindung der Personen 10. D dazu im Einzelfall künstlich erfunden. Fragestellung IV. Mit einer gegebenen Anzahl der Dinge die Veränderungen der Ordnung finden. Gleichwie der Gäste am Tisch 6 bei Jeremias Drexel, 7 bei Georg Philipp Harsdörffer, 12 bei Georg Henisch. Die Proteus-Verse, z. B. die von Bernardus Bauhusius, von Thomas Lansius, von Heinrich Christoph Ebell, von Giovanni Battista Riccioli, von Georg Philipp Harsdörffer. Das Vertauschen der Buchstaben des Alphabets, die Zusammenstellungen der Atome, die Mosaiksteinchen der Grammatik. Fragestellung V. Bei gegebener Anzahl Dinger die Veränderungen der Nachbarschaft zu finden. Der ehrenvollste Platz in einer Runde. Der syllogistische Zirkelschluss. Fragestellung VI. Begeben ist die Anzahl der zu verändernden Dinge, welche irgendetwas oder irgendwelche wiederholt werden, die Vertauschung der Reihenfolge zu finden. Gattungen der Hexameter 76. Des Hexameter 26. Deren Buchstaben dem vorhergehenden folgend übertrifft Publilius Optatianus Porfyrius: davon jener. Doppellaute aus der Schrift. Fragestellung VII. Veränderungen beim gegebenen Hauptsatz zu entdecken. Fragestellung VIII. Gewöhnliche Veränderungen dem gegebenen anderen Hauptsatz. Fragestellung IX. Hauptsätze, die gewöhnliche Veränderungen haben. Fragestellung X. Hauptsätze der brauchbaren und unbrauchbaren Veränderungen. Fragestellung XI. Unbrauchbare Veränderungen. XII. Brauchbare. Die Proteus-Verse des Publilius Optatianus Porfyrius (beiläufig dem Virgil), des Julius Caesar Scaliger (beiläufig dem Virgil), des Bernardus Bauhusius (beiläufig dem Ovid), des Gregor Kleppis (Verfahren zur Unterscheidung brauchbarer und unbrauchbarer), des Carl von Goldstein / Matthäus Reimer, des Christian Daum 4, deren beiden letzten mehr als Proteus.
Einleitung.
Mit Gott!
Die Metaphysik, damit ich mit dem höchsten beginne, behandelt bald das Seiende, bald die Zustände des Seienden; weil aber die Zustände des natürlichen Körpers keine Körper sind, so sind die Zustände des Seienden keine Seienden. Der Zustand des Seienden ist aber (oder das Maß) durch eine andere unabhängige, die Qualität genannt wird, durch eine andere bezogene, und diese Eigenschaft bezieht sich entweder auf ihren Teil, den sie hat, Quantität, oder die Eigenschaft zu einer anderen Sache, Beziehung, um es gleichwohl genauer zu sagen, der zugrunde zu legende Teil ist gewissermaßen vom Ganzen unterschieden, auch die Menge der Sachen ist eine Beziehung zum Teil. Deswegen ist es offensichtlich, dass es weder die Qualität noch die Quantität, noch die Beziehung der Seienden sind, deren Behandlung aber in der bezeichneten Wirkung zur Metaphysik gehören. Ferner ist alle Beziehung entweder Vereinigung oder Zusammenhang. Aber die Dinge, zwischen denen eine Beziehung besteht, in der Vereinigung werden sie Teile genannt, zusammen mit der Vereinigung sind sie das Ganze. Mit diesem trifft zu, so oft wir vieles zugleich wie ein Gesamtes zugrunde legen. Aber das Eine wird verstanden, was wir auch immer durch eine einzige Tat des Verstands oder zugleich erwägen, z. B. auf welche Weise auch immer wir irgendeine beliebig große Zahl häufig blindlings durch einen gewissen Gedanken zugleich begreifen, freilich die Ziffern auf dem Papier zu lesen, für wen ist nicht klar zu erkennen, dass Methusalem freilich nicht ein Lebensalter zu verleihen wäre. Abgezogen aber von einem ist die Einheit, und das Ganze selbst abgezogen aus den Einheiten oder die Gesamtheit Zahl genannt wird. Die Menge ist also die Anzahl der Teile. Daher ist offensichtlich, dass in der Sache selbst die Menge und die Anzahl zusammenfallen, doch jene manchmal gleichsam äußerlich, dass durch die Beziehung oder das Verhältnis zu jenem beschrieben werden, im Hilfsmittel nämlich solange die Anzahl der Teile nicht erkannt wird. Und diese Ursache ist die scharfsinnige Lehre von den Verhältnissen und Proportionen, was zuerst René Descartes zur Entfaltung gebracht hat, danach Frans van Schooten d. J. in Regeln hergeleitet hat, und Erasmus Bartholin diese durch allgemeine mathematische Elemente, wie er es nennt. Und deswegen ist die Lehre von den Verhältnissen und Proportionen, oder die nicht beschriebene Menge; die Arithmetik von der beschriebenen Menge oder den Anzahlen; aber die Scholastiker haben fälschlich geglaubt die Zahl entsteht nur durch fortgesetzte Teilung und kann nicht auf unkörperliche angewandt werden. Die Zahl ist nämlich gleichsam ein gewisses unkörperliches Symbol, entstanden aus der Vereinigung irgendwelcher Seienden, z. B. Gott, Engel, Menschen, Bewegung, die gleichzeitig 4 sind. Weil demnach die Zahl irgendetwas völlig allgemeines wäre, aus gutem Grunde zur Metaphysik gehört, wenn man die Metaphysik als Lehre derer anerkennt, die allen Arten der Seienden gemeinsam sind. Denn die mathematische Wissenschaft (damit deren Name jetzt verstanden wird) um genau zu sprechen, ist nicht ein Lehrgebiet, sondern die Menge aus verschiedenen entnommenen Teilen von einzelnen Disziplinen in Bearbeitungen, die verdientermaßen nahe bei der Erkenntnis verschmolzen sind. Denn wie die Arithmetik wie auch die Analysis die Menge der Seienden behandeln, so behandelt die Geometrie die Menge der Körper, oder des Raumes, der von den Körpern aufgespannt ist. Die staatliche Einteilung aber der Lehrgebiete in Berufsgruppen, die eher nach der Zweckmäßigkeit der Lehre als der natürlichen Ordnung zugeschnitten ist, fehlte dass wir sie untergraben. Im Übrigen kann das Ganze selbst (und so die Anzahl oder Gesamtheit) völlig zerrissen werden in kleinere Teile, das ist die Grundlage der Zusammensetzungen, wenn man nur versteht dass selbst in den verschiedenen kleinsten alle gemeinsamen Teile gegeben werden, z. B. das Ganze sei A, B, C, es werden alle kleineren sein, deren Teile AB, BC, AC sein werden: und selbst der kleinsten Teile, oder für die Anordnung der geringsten zugrunde gelegten (nämlich der Gesamtheit) unter einander und mit dem Ganzen, die Zustand genannt wird, kann verändert werden. So entstehen zwei Arten Veränderungen, der Zusammenfassung und des Zustands. Und sowohl die Zusammenfassung wie der Zustand gehören zur Metaphysik, nämlich zur Lehre vom Ganzen und den Teilen, wenn sie an sich betrachtet werden; wenn wir aber die Veränderung betrachteten, das ist die Menge der Veränderung, auf die die Zahlen und die Arithmetik anzuwenden ist. Aber ich würde meinen, die Lehre der Zusammenfassung passt besser zur reinen Arithmetik, der Zustand zum geformten, denn auf diese Weise können die Gesamtheiten als eine Linie zu erzeugen verstanden werden. Obschon ich hier beiläufig anmerken möchte, die Gesamtheiten können entweder durch die Art der geraden Linie, oder als Kreis oder eine andere Linie oder Linien, die in sich zurückkehren oder eine geschlossene Figur dargestellt werden, die vorigen durch eine Art Anordnung im vollkommenen Zustand oder der Teile mit dem Ganzen; Die folgenden durch den bezogenen Zustand oder der Teile zu den Teilen, durch Nachbarschaft, auf welche Weise sie sich unterscheiden werden wir unten bei den Definitionen 4 und 5 erklären. An dieser Stelle reichen sie als Vorwort aus, wie diese in der Lehre der Materie deren Gebäude wäre, wird offensichtlich.
Definitionen.
- Die Veränderung an dieser Stelle ist die Umwandlung der Verhältnisse. Denn die Umwandlung heißt andere Substanzen, andere Menge, andere Eigenschaft; andere wandelt nichts in der Sache um, sondern nur bezüglich der gegenseitigen Anordnung, den Zustand, die Verbindung mit anderen irgendwo.
- Die Veränderbarkeit ist selbst die Anzahl aller Veränderungen. Denn die Begriffe der Möglichkeiten an sich genommen bestimmen die Anzahl derer, denn dergestalt wird in der Mechanik häufig gesprochen, dass die Möglichkeiten zweier Maschinen das doppelte der einzelnen seien.
- Zustand ist die örtliche Anordnung der Teile.
- Der Zustand ist entweder absolut oder relativ bezogen: jenes der Teile zum Ganzen, dieses der Teile zu den Teilen. In jenem wird die Anzahl der Plätze und die Entfernung vom Anfang und vom Ende betrachtet, darunter wird weder der Anfang noch das Ende verstanden, sondern man betrachtet wie groß der Abstand der Teile von einem gegebenen Teil ist. Daher wird jenes durch eine Linie oder eine lineare Figur ausgedrückt, die nicht geschlossen sind und nicht in sich zurückgehen, und am besten durch eine gerade Linie; diese durch eine Linie oder eine geschlossene lineare Figur, und am besten durch einen Kreis. In jenem haben Vorrang und Nachrang das größte Verhältnis, in diesem keines. Deshalb hat man zu jenem höchste Ordnung gesagt.
- Diesem die Nachbarschaft, jenem die Anordnung, diesem die Zusammensetzung. Deswegen unterscheiden sich die folgenden Zustände durch das Verhältnis der Anordnung: abcd, bcda, cdab, dabc. Aber in der Nachbarschaft wird keine Veränderung sondern ein Zustand verstanden, dieser nämlich: Weil der sehr witzige Friedrich Taubmann, als er Dekan der philosophischen Fakultät war, wird in Wittenberg gesagt öffentlich eine Reihe von Ankündigungen der Anwärter für das Lehramt einen Zuhörerkreis bildete mit einer Gliederung des Inhalts, den nicht die begierigen Leser nicht verstanden, der auf den Misthaufen gehörte.
- Die Veränderbarkeit der Ordnung verstehen wir etwa, wenn wir die Veränderungen entsprechend der Bedeutung von z. B. 4 Dingen auf 24 Arten umgestellt werden können. [24 = 4! = 1 · 2 · 3 · 4]
- Die Veränderbarkeit der Verknüpfungen nennen wir Zusammenfassung, z. B. 4 Dinge können auf 15 verschiedene Weisen miteinander verbunden werden [1 + 2 + 4 + 8 = 20 + 21 + 22 + 23 = 15].
- Die Anzahl der zu verändernden Dinge nennen wir vereinfacht Anzahl, z. B. 4 im vorgestellten Falle.
- Die Zusammenfassung ist die kleinste Einheit im größeren Gesamten, wie wir in der Einleitung dargelegt haben.
- Dass aber eine gewisse Zusammenfassung bestimmt wird, ist das größere Ganze in gleiche untergeordnete Teile zu zerlegen damit die kleinsten (das ist welche nun allerdings nicht weiter geteilt werden), aus denen die Zusammenfassung oder das kleiner Ganze zusammengesetzt wird und deren unterschiedliche Anordnung verändert wird; weil daher das Ganze selbst weniger. Mehr oder weniger ist, je nachdem viele Teile an Stelle eines hinein gehen, nenne wir die Anzahl der gleichzeitig oder einmalig zusammenzufassenden Teile oder Einheiten den Exponenten, nach dem Beispiel der geometrischen Progression, zum Beispiel sei das Ganze ABCD. Wenn alle kleineren aus2 Teilen bestehen sollen, z. B. AB, AC, AD, BC, BD, CD, sei der Exponent 2, wenn aber aus 3, z. B. ABC, ABD, ACD, BCD, wird er Exponent 3 sein.
- Bei gegebenem Exponenten werden wir die Zusammenfassungen so schreiben: wenn der Exponent 2 ist. Zusammen2fassung; wenn er 3 ist Zusammen3fassung; wenn er 4 ist Zusammen4fassung und so weiter.
- Zusammenfassungen werden einfach aus den Exponenten aller Zusammenfassungen berechnet, z. B. 15 (für die Anzahl 4) die zusammengesetzt werden aus 4 (Einheit), 6 (Zusammen2fassung), 4 (Zusammen3fassung), 1 (Zusammen4fassung).
- Eine brauchbare (unbrauchbare) Veränderung ist welche wegen der zugrundeliegenden Materie keinen Platz haben kann, z. B. 4 Bestandteile können 6 Mal zusammen2gefaßt werden; aber 2 Zusammen2fassungen sind unbrauchbar, von denen werden gegensätzliche Feuer, Wasser, Luft, Erde zusammen2gefaßt.
- Die Klasse der Dinge ist weniger als das Ganze, sie besteht aus wenigsten drei übereinstimmenden Dingen, sowie aus Teilen, doch so dass die übrigen Klaasen gegensätzliche Dingen enthalten, z. B. oben in der Fragestellung 3, wo wir die Klassen der Meinungen im Bezug auf das höchste Gute bei B. Augustinus von Hippo abhandeln werden.
- Der Hauptsatz der Veränderung ist die Stellung gewisser Teile; die Regel der Veränderung vom allem was sie in den meisten Veränderungen innehat, siehe unten in der Fragestellung 7.
- Gemeinsame Veränderungen sind, in welchen viele Hauptsätze übereinstimmen, siehe unten Fragestellungen 8 und 9.
- Ein gleichartiges Ding ist, was an der gegebenen Stelle gleich darstellbar ist außer im Hauptsatz, einstimmige aber was keine Gleichartigkeit hat, siehe Fragestellung 7.
- Ein Hauptsatz wird vervielfältigbar genannt, dessen Teile verändert werden können.
- Ein wiederholtes Ding ist, was in der gleichen Veränderung öfter gesetzt wird, siehe Fragestellung 6.
- Wir bezeichnen durch das Symbol + die Addition, - die Subtraktion, ᴖ die Multiplikation, ᴗ die Division, f ist macht oder Summe, = die Gleichheit. Bei den beiden ersten und im letzten stimmen wir mit René Descartes, den Algebraikern und anderen überein; die anderen Symbole hat Isaac Barrow in seiner Euklid-Ausgabe , Cambridge, Oktav, im Jahr 1655.
Fragestellungen
Es gibt drei, die betrachtet werden müssen: Fragestellungen, Lehrsätze, Gebrauch; bei einzelnen Fragestellungen haben wir den Gebrauch angehängt; wo immer der Aufwand und der Lehrsatz als wert betrachtet wurde. Die Fragestellung aber fügen wir gewisse Überlegungen zur Lösung an. Von diesen verdanken wir einen früherer Teil den ersten, dem zweiten und dem dritten anderen, die übrigen haben wir selbst erforscht. Wer jene zuerst gefunden hat wissen wir nicht. Daniel Schwenter Deliciae physico-mathematicae oder mathematische und philosophische Erquickstunden l. 1. Sektion I Satz 32 sagt Gerolamo Cardano, Johannes Buteo und Niccolò Tartaglia ragen heraus. Jedoch finden wir nichts bei Gerolamo Cardano "Übungen zur Arithmetik", die er 1539 in Mailand herausgegeben hat. Besonders klar, was immer neulich gehalten wird, hat es Christophorus Clavius in "In Sphaeram Ioannis de Sacro Bosco commentarius" vorgetragen (Herausgegeben in Rom im Format Quart im Jahr 1585, Seite 33 und folgende).
Fragestellung I.
Aus der gegebenen Anzahl und dem Exponenten die Zusammenstellungen zu finden.
Es gibt zwei Vorgehensweisen der Lösung, eine von allen Verknüpfungen, die andere nur aus den Zusammenstellungen: jene ist freilich allgemeiner, diese aber erfordert weniger Angaben, nämlich nur die Anzahl und den Exponenten, weil jene auch die gefundenen Verknüpfungen voraussetzt.
Die allgemeinere Vorgehensweise haben wir uns selbst ermittelt, die spezielle ist allgemein bekannt. Die Lösung für jene ist so beschaffen: "Die vorhergehenden Verknüpfungen des Exponenten und der gegebenen von der vorhergehenden Anzahl werden addiert, das Ergebnis werden die gesuchten Verknüpfungen sein." zum Beispiel soll die gegebene Anzahl 4 sein und der gegebene Exponent 3, werden sie zu der vorhergehenden Zahl 3 Zusammenstellungen von 2 3 und die Zusammenstellung von 3 1 (3 + 1 macht 4), das gesuchte Ergebnis wird 4 sein.
Aber weil die Verknüpfungen der vorhergehenden Zahl erforderlich sind, kann man die Tabelle אּ aufgestellt werden, in der die oberste Zeile enthält von links nach rechts die Zahlen von 0 bis einschließlich 12, denn wir haben gemeint, dass es leicht ist von hier fortzuschreiten, wie es leicht ist fortzusetzen; die Spalte äußerst links enthält von oben nach unten die Exponenten von 0 bis 12, die untere Zeile enthält von links nach rechts die einfachen Verknüpfungen.
Exponenten |
0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | Complexiones |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 n | 8 u | 9 m | 10 e | 11 r | 12 i | ||
| 2 | 0 | 0 | 1 | 3 | 6 | 10 | 15 | 21 | 28 | 36 | 45 | 55 | 66 | ||
| 3 | 0 | 0 | 0 | 1 | 4 | 10 | 20 | 35 | 56 | 84 | 120 | 165 | 220 | ||
| 4 | 0 | 0 | 0 | 0 | 1 | 5 | 15 | 35 | 70 | 126 | 210 | 330 | 495 | ||
| 5 | 0 | 0 | 0 | 0 | 0 | 1 | 6 | 21 | 56 | 126 | 252 | 462 | 792 | ||
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 7 | 28 | 84 | 210 | 462 | 924 | ||
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 8 | 36 | 120 | 330 | 792 | ||
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 9 | 45 | 165 | 495 | ||
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 10 | 55 | 220 | ||
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 11 | 66 | ||
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 12 | ||
| 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | ||
| * | 0 | 1 | 3 | 7 | 15 | 35 | 63 | 127 | 255 | 511 | 1023 | 2047 | 4095 | ||
| † | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 |
stellungen bei gegebenem Exponenten) durch Zufügen der 1,
die mit den Werten der geometrischen 2-er Folge zusammen fallen †.
Die übrigen Zeilen zwischen diesen enthalten die Zusammenstellungen von der gegebenen Anzahl die sich im Gipfel unbedingt entspricht, und dem Exponenten womit aus der linken Richtung. Die Begründung der Lösung, und die Grundlage der Tabelle wird offenbar sein, wenn wir es bewiesen haben werden, die Verknüpfungen der gegebenen Zahlen und des Exponenten entstehen aus der Summe der Verknüpfungen von der vorangehenden Zahl des Exponenten und den vorangehenden und den gegebenen. Denn es sei die gegebene Zahl 5, der gegebene Exponent 3, die vorhergehende Zahl wird 4 sein, diese hat 4 Zusammenstellungen von 3 nach Tabelle אּ, 6 Zusammenstellungen von 2. Nun hat die Nummer 5 alle Zusammenstellungen von 3 welche vorangehen nämlich 4 (denn im Ganzen wird auch der Teil umfasst), und außerdem so viel wie die vorhergehende Verknüpfungen von 2 hat, denn die neue Differenz um welche die Zahl 5 die 4 übersteigt, wird den einzelne Verknüpfungen von 2 dem hinzugefügt, macht eben so viele neue Zusammenstellungen von 3, nämlich 6 + 4 macht 10. Also Zusammenstellungen der gegebenen Anzahl u. s. w. Was zu beweisen war.
Wir fügen für mehr Klarheit die Tabelle בּ hinzu, wo wir auf den querliegenden Zeilen die Zusammenstellung von drei von 3, und von 4 und von 5 unterschieden haben, doch so wie die ersten Zusammenstellungen von 3 den folgenden gemeinsam seien, und als Folge in der gesamten Tabelle die Anzahl der Zusammenstellungen von 3 fünf wäre, und damit offenbar geworden wäre, welche Zusammenstellungen von 3 der folgenden Anzahlen aus der vorausgegangenen Zusammenstellungen von 2 durch Hinzufügen von einem einzigen neuen Fremden entstehen, in der Spalte nach unten strebend haben wir die Zusammenstellungen vom neuen Fremden unterschieden.
|
Zahl der Verknüpfungen von 3
|
1 | ab | c | 3 |
| 2 | ab | d | Dinge |
|
| 3 | ac | d | ||
| 4 | bc | d | ||
| 5 | ab | e | 4 | |
| 6 | ac | e | ||
| 7 | ad | e | Anzahl |
|
| 8 | bc | e | ||
| 9 | bd | e | ||
| 10 | cd | e | 5 |
Wir werden hier Lehrsätze hinzufügen deren Tatsache aus der Tabelle אּ offensichtlich ist, der Grund aus der Grundlage der Tabelle:
- Wenn der Exponent größer ist als die Zahl, ist die Zusammenstellung 0.
- wenn er gleich ist, ist jene 1.
- Wenn der Exponent um 1 kleiner als die Zahl ist, sind Zusammenstellung und Zahl dasselbe.
- Allgemein gilt: Zwei Exponenten, in denen die Zahl zerlegt werden kann, oder die einander zur Zahl ergänzen, dieselben haben Verknüpfungen von jener Zahl. Denn weil bei den kleinen Exponenten 1 und 2, in die die Zahl 3 zerlegt wird, das aber wäre wirklich der Fall, nach Tabelle ח, die anderen aber entstehen durch Addition nach Fragestellung 1, wenn die gleichen (3 und 3) addiere die gleichen (oberhalb 1 und unterhalb 1), es werden gleiche erzeugt (3 + 1 macht 4), und ebenso wird es gemacht bei den übrigen bei Notwendigkeit.
- Wenn die Zahl ungerade ist, werden darin zwei benachbarte Verknüpfungen gegeben, die sich nahezu gleich sind; wenn aber gerade, trifft das nicht zu. Denn die ungerade Zahl kann zerlegt werden in zwei benachbarte Exponenten die sich um 1 unterscheiden, z. B. 1 + 2 macht 3; die gerade aber kann es nicht, sie sind dieselben. Denn benachbarte, in welche sie halbiert werden gerade kann, sind dieselben. Weil also die ungerade Zahl in zwei Exponenten geteilt werden kann, haben hier zwei benachbarte Zusammenstellungen nach Lehrsatz 4, weil jene um 1 entfernt sind.
- ie Zusammenstellungen nehmen zu bis zur Zahl die die Hälfte der Exponenten ist oder der Hälfte von zwei benachbarten von da an nehmen sie wieder ab.
- Alle ersten Zahlen bemessen ihre besonderen Zusammenstellungen (oder vom gegebenen Exponenten).
- Alle Zusammenstellungen sind einfach ungerade Zahlen.
| ab | ac | ad | ae | af |
| bc | bd | be | bf | |
| cd | ce | cf | ||
| de | df | |||
| ef |
Es verbleibt der andere der gewissermaßen besondere Teil der Fragestellung: " zu einer gegebenen Zahl A die Zusammenstellungen B zu finden. Die Lösung: Wird die Zahl mal genommen mit ihrer um 1 verminderten Zahl, davon die Hälfte wird das gesuchte sein, (A · (A - 1)) ⁄ 2 = B. es sei zum Beispiel die Zahl A = 6, 6 · 5 macht 30 ⁄ 2 macht 15." Zusammenstellungen von 2 der 6 Dinge abcdef aufgezählt werden; aber die erste Sache a genommen ergibt mit den anderen 5 Zusammenstellungen von 2, die Zahl ist um eins geringer; die zweite b vor die anderen gezogen nur 4, denn es kann nicht vor das vorangehende a gezogen werden, denn das würde zurückführen zur vorigen Zusammenstellung ba oder ab (denn diese unterscheidet sich nicht in Hinsicht der Zusammenstellung), also allein in den nachfolgenden die 4 ergeben, genauso die dritte c vor die folgenden gezogen macht 3, die vierte d ergibt 2, die fünfte e und letzte f ergibt 1. Es gibt daher 5 + 4 + 3 + 2 + 1 macht 15 Zusammenstellungen von 2. So ist offensichtlich, dass die Anzahl der Zusammenstellungen zusammengesetzt wird aus den Gliedern einer arithmetischen Reihe, deren Unterschied 1 ist, gezählt von 1 bis zur Zahl der Dinge einschließlich der Grenzen, oder aus allen Zahlen der Anzahl der kleineren Dinge zugleich zusammengezählt. Aber weil, wie die Arithmetiker gewöhnlich lehren, solche Zahlen werden in dieser Zusammenstellung zusammengezählt, dass die größte Zahl multipliziert wird mit der nächst größeren, halbiert wäre das gesuchte, und das nebenstehende ist freilich an dieser Stelle selbst die Zahl der Dingen, deshalb ist ebenso wenn man so sagen will, die Zahl der Dingen mit dem nächst kleineren zu multiplizieren, und die Hälfte wird das gesuchte sein.
Fragestellung II.
Aus der gegebenen Anzahl die Zusammenstellungen einfacher zu finden.
Die gegebene Zahl soll gesucht werden unter den Exponenten einer geometrischen Reihe zur Basis 2, die Zahl oder das Glied dieser Reihe, das mit dem übereinstimmt aus dem Abschnitt um die Einheit verringert wird das gesuchte sein. Die Ursache, oder der Grund ist schwierig teils zu verstehen, teils wenn man sie versteht, zu erklären: die Tatsache ist mit Tabelle א offensichtlich. Denn immer einzelne gleichzeitig zugefügte Zusammenstellungen, von der zugefügten Einheit, stellen immer Glieder der geometrischen Reihe zur Basis 2 dar, deren Exponent die gegebene Zahl sei. Denn die Erklärung, wenn irgendein Neugieriger es erkunden würde, wird zu suchen sein in der Zerlegung in der üblichen italienischen Praxis der Arithmetik, vom Zerlegen (Faktorenzerlegung). Diese muss so beschaffen sein, dass das gegebene Glied der geometrischen Folge zuerst in ein Teil mehr zerlegt wird, als es Einheiten ihres Exponenten gibt, das heißt die Anzahlen der Dinge, welche immer gleich seien vom ersten zum letzten, das zweite dem vorletzten, das dritte dem vor-vorletzten und so weiter, solange bis entweder, wenn die Zahl der Dinge in geradzahlige zerlegt worden ist, der Exponent oder die Zahl der Dinge ungerade entsteht, in der Mitte entsprechen zwei Teile nach Fragestellung 1, Theorem 5 (z. B. 128 durch 7 in 8 Teile zerlegt werden gemäß Tabelle א: 1, 7, 31, 35, 21, 1), oder wenn in ungeradzahlige, entsteht durch den geradzahligen Exponenten, bleiben in der Mitte eines das keinem entspricht (z. B. 256 werden von 8 zerlegt in 9 Teile gemäß Tabelle א: 1, 8, 28, 56, 70, 56, 28, 8, 1). Irgendjemand glaubte, daraus sei offensichtlich ein neues Verfahren und dieses die vollständige Lösung der Fragestellung 1 oder aus dem gegebenen Exponenten einfach die Anzahl der Zusammenstellungen oder die Glieder der geometrischen Folge zur Basis 2 gemäß dem gegebenen Vorgehen; jedoch sind die Angaben nicht ausreichend, und dieselbe Zahl kann in wieder andere Teile zerlegt werden, doch nach derselben Regel.
Anwendungen der Fragestellungen I und II.
Weil alles was ist oder gedacht werden kann, in der Regel aus Teilen zusammengesetzt würde entweder gegenständlich oder wenigstens gedanklich, ist es notwendig, welche sich durch die Beschaffenheit unterscheiden oder in denen unterscheiden, die andere Teile enthalten, und hier der Gebrauch der Zusammenstellungen, oder was an anderer Stelle, hier der Anordnungen, dort durch Verschiedenheit der Materie, hier der Form beurteilt wird. Allerdings werden durch den Einfluss der Zusammenstellungen nicht nur die Beschaffenheiten der Dinge gefunden, sondern auch die Eigenschaften, dass so beinahe der ganze erfinderische Teil der Logik dort auf einfache Begriffe, hier auf umschriebene begründet wird durch die Zusammenstellungen, mit einem Wort sowohl durch die Lehre der Zerlegungen wie durch die Lehre der Darlegungen. Geschweige denn, wie sehr der Teil logischer Analyse oder sorgfältige Beurteilung von syllogistischen Verfahren hoffen wir durch Untersuchung im Beispiel 6 darzustellen.
Bei der Zerlegung der Zusammenstellungen gibt es drei Verfahren: 1. Von der gegebenen Grundlage mit einer einzigen Zerlegung deren Beschaffenheit zu finden; 2. Durch viele gegebene Zerlegungen von derselben Gattung, die Art zu finden aus verschiedenen gemischten Zerlegungen, was wir jedoch für die Fragestellung 8 vorbehalten werden; 3. Von gegebenen Arten die untergeordneten Eigenschaften zu finden. Die Beispiele sind über die gesamte Philosophie verstreut, dass sie sogar der Jurisprudenz nicht fehlen werden wir zeigen, bei den Medizinern aber entstehen alle Vielfalten der zusammengesetzten Heilmittel und Pharmazeutika aus der Mischung verschiedener Zutaten, aber es ist die Aufgabe durch größte Urteilskraft die nützlichen Mischungen auszuwählen. Zuerst werden wir daher Beispiele dieser Überlegung auf die zu findenden Gattungen geben:
- Bei den Rechtsberatern l. 2. D. Mandati et pr. J. de Mandato wird die folgende Aufteilung vorgeschlagen: der Auftrag wird auf 5 Weisen herbeigeführt: durch die Dank des Auftraggebers, des Auftraggebers und des Anwalts, eines Dritten, des Auftraggebers und des Dritten, des Anwalts und des Dritten. Die Hinlänglichkeit deren Aufteilung werden wir so versuchen zu finden: deren Grundlage ist sein Ende oder welcher Person die Begünstigung erwiesen wird, davon gibt es drei: Auftraggeber, Beauftragter und der Dritte. Die Zusammenstellungen der Dinge aber sind sieben: die drei Vereinigungen: mit nur einem 1) des Auftraggebers, 2) des Anwalts, 3) des Dritten wird Begünstigung erwiesen. Ebenso viele Zusammenstellungen von 2: 4) des Auftraggebers und des Anwalts, 5) des Auftraggebers und des Dritten, 6) des Anwalts und des Dritten Begünstigung. Zusammenstellungen von 3 gibt es eine, nämlich die 7. Sowohl des Auftraggebers als auch des Anwalts und des Dritten gleichzeitige Begünstigung. Ebenso viele Zusammenstellungen von 2: 4) des Auftraggebers und des Anwalts, 5) des Auftraggebers und des Dritten, 6) des Anwalts und des Dritten Begünstigung. Zusammenstellungen von 3 gibt es eine, nämlich die 7. sowohl des Auftraggebers als auch des Anwalts und des Dritten gleichzeitige Begünstigung sowohl des Auftraggebers als auch des Anwalts und des Dritten gleichzeitige Begünstigung. Hier weisen die Rechtsberater jene Vereinigung als unbrauchbar zurück, in der nur die Begünstigung des Anwalts berücksichtigt ist, weil der Rat wichtiger wäre als der Auftrag; es verbleiben deshalb 6 Arten, aber warum 5 übrigbleiben, die Zusammenstellung von 3 übergangen wird, weiß ich nicht.
-
 Die Anzahl der Urstoffe, oder die veränderbaren Arten einfacher Körper leitet Aristoteles im 2. Buch " Über das Entstehen und das Vergehen" mit dem Pytagoräer Ocellus Lucanus aus der Anzahl der Grundeigenschaften ab, welche er vier zu sein unterstellt, sowie von derGrundlage, doch diese durch Gesetze, dass 1) ein beliebiges zusammengesetzt würde aus zwei Eigenschaften und nicht aus mehr oder weniger; daher ist es offensichtlich die Vereinigungen von 2, Vereinigungen von 3 und 4 sind zuverwerfen, einzig die Vereinigungen von 2 sind beizubehalten, welche 6 sind; 2) dass niemals in einer Verbindung von 2 gegensätzliche zusammen kommen, daher werden wiederum zwei Verbindungen unbrauchbar, weil zwischen diesen zwei gegensätzliche Grundeigenschaften angegeben werden, deshalb verbleiben 4 Verbindungen von 2, das ist die Anzahl der Grundstoffe. Wir haben eine Übersicht dazu gefügt (siehe die Seite neben dem Titel dieser Abhandlung), in der die Abstammung aus den Grundeigenschaften gut gezeigt wird. Ferner wie Aristoteles aus diesen jene, so Galenos von Pergamon aus jenen 4 Temperamenten, und deren verschiedenen Mischungen die nachfolgenden Mediziner hervorgebracht haben, denen allen sich schon im vorigen Jahrhundert Claudius Campensius in " Betrachtungen des Natürlichen bei Aristoteles" entgegengestellt hat und Galenos von Pergamon Zugabe zu den Kommentaren dessen in den "Lehrsätze des Hippocrates" herausgegeben im Oktav in Lyon im Jahre 1576.
Die Anzahl der Urstoffe, oder die veränderbaren Arten einfacher Körper leitet Aristoteles im 2. Buch " Über das Entstehen und das Vergehen" mit dem Pytagoräer Ocellus Lucanus aus der Anzahl der Grundeigenschaften ab, welche er vier zu sein unterstellt, sowie von derGrundlage, doch diese durch Gesetze, dass 1) ein beliebiges zusammengesetzt würde aus zwei Eigenschaften und nicht aus mehr oder weniger; daher ist es offensichtlich die Vereinigungen von 2, Vereinigungen von 3 und 4 sind zuverwerfen, einzig die Vereinigungen von 2 sind beizubehalten, welche 6 sind; 2) dass niemals in einer Verbindung von 2 gegensätzliche zusammen kommen, daher werden wiederum zwei Verbindungen unbrauchbar, weil zwischen diesen zwei gegensätzliche Grundeigenschaften angegeben werden, deshalb verbleiben 4 Verbindungen von 2, das ist die Anzahl der Grundstoffe. Wir haben eine Übersicht dazu gefügt (siehe die Seite neben dem Titel dieser Abhandlung), in der die Abstammung aus den Grundeigenschaften gut gezeigt wird. Ferner wie Aristoteles aus diesen jene, so Galenos von Pergamon aus jenen 4 Temperamenten, und deren verschiedenen Mischungen die nachfolgenden Mediziner hervorgebracht haben, denen allen sich schon im vorigen Jahrhundert Claudius Campensius in " Betrachtungen des Natürlichen bei Aristoteles" entgegengestellt hat und Galenos von Pergamon Zugabe zu den Kommentaren dessen in den "Lehrsätze des Hippocrates" herausgegeben im Oktav in Lyon im Jahre 1576.
- Gewöhnlich werden Zahlen von den Arithmetikern unterschieden in Zahlen im Sinne des Wortes (natürliche Zahlen) wie 3, Brüche wie ⅔, irrationale wie √3, das ist die Zahl, die mit sich selbst multipliziert 3 ergibt, wie sie in der Natur nicht vorkommt, aber durch Entsprechung verstanden wird, und benannte, die andere geformt nennen, z. B. Quadrat, Kubik, und Pronische Zahl. Aus der Mischung derer macht Gerolamo Cardano in Kapitel 2 seiner "Praxis der Arithmetik" elf gemische Arten. Es gibt deshalb im Ganzen 15 Zusammenstellungen, nämlich 4 Vereinigungen, die wir benannt haben, 6 Zusammenstellungen von 2: ganze Zahl und Bruch, z. B. 3 ⁄ 2 oder 1 ½; ganze Zahl und Wurzel Zahl, z. B. 7 · √3, ganze Zahl und Potenz, z. B. 3 + a3; Wurzel Zahl und Potenz, z. B. 3. Potenz von 7; 4 Zusammenstellungen von 3: ganze Zahl und Bruch und Wurzel Zahl, ganze Zahl und Bruch und Potenz, ganze Zahl und Wurzel Zahl und Potenz, Bruch und Wurzel Zahl und Potenz; 1 Zusammenstellung von 4: ganzer Zahl und Bruch und Wurzel Zahl und Potenz. An Stelle des Ausdrucks: Zahl, wird angemessener der Begriff: ganze Zahl eingesetzt werden. Schon ist 4 + 6 +4 + 1 macht 15.
- Das Register, auf deutsch ein Zug, wird in pneumatischen Orgeln ein gewisser Henkel genannt, durch dessen Öffnung der Ton verändert wird, allerdings nicht die Melodien an sich oder in Hinsicht auf die Tonhöhe, sondern durch das Verhältnis der Kanäle, wie die Art der Schwebung, nach Art dämpfend u. s. w. bewirkt werden. Solche sind durch den Fleiß der Jüngeren über 30 gefunden worden. Deshalb sollen in irgendeiner Orgel so viele wie 12 einfache, ich behaupte dass in der Welt gewissermaßen 4.095 sein werden; denn so viele sind die einfachen Verknüpfungen der 12 Dinge nach Tabelle א, die bedeutenden Organisten, öffnen nun manchmal mehr, manchmal weniger, manchmal diese manchmal jene gleichzeitig , um die Töne zu verändern.
- Thomas Hobbes Elementorum Philosophiae Sectio Prima De Corpore Teil 1, Kapitel 5. Die Dinge, deren Begriffe im Vordersatz beginnend gegeben werden, oder in seinem Stile, bezeichnete, deren Namen gegeben werden, teilt in Körper (das sind Substanzen, denn alle Substanz ist selbst ein Körper), Eigenschaften, Vorstellungen und Namen, und so gehören Namen entweder der Körper, z. B. Mensch, oder der Eigenschaften, z. B. alles Gegenstandslose, Vernunft, Bewegung, oder Vorstellungen, auf welche sich Raum, Zeit, alle fühlbaren Eigenschaften u. s. w. beziehen oder Namen, bezieht er auf welche sich sekundäre Absichten. Weil diese untereinander sechsmal zu zweien verbunden werden, entstehen ebenso viele Arten der Behauptungen, und diesen hinzugefügt, wenn sie zu einheitlichen Begriffen verbunden werden (und der Körper einem Körper zugeteilt wird, die Eigenschaft der Eigenschaft, die Vorstellung der Vorstellung, die sekundäre Kenntnis der sekundären Kenntnis), nämlich 4, entstehen 10. Aus diesen werden einzigen einheitlichen Begriffen nützlich verbunden beobachtet Thomas Hobbes. Was, wenn es so ist, wie es die sichere und allgemeine Philosophie verkündet, das Abstrakte und das Konkrete, die Eigenschaft und die Substanz, die erste und die sekundäre Erkenntnis schlecht gegenseitig erklärt werden, wird dies nützlich sein zur Erfindungskunst der Behauptungen, oder der Auswahl der Verbindungen: dem Erkennen der brauchbaren aus unzähligen Bagatelldingen; darüber unten.
-
Ich komme zu einem kaum weniger verwickelten Beispiel der Verbindungen: der Bestimmung der Anzahl der Verfahren unbedingter Syllogismen. In welche Sache Johannes Hospinianus von Stein neue Überlegungen ausgelöst hat, Professor für Orgel in Basel, ein Mann der geringsten gewöhnlichen Betrachtungen in einem wenig beachteten Büchlein, herausgegeben im Oktavformat in Basel im Jahre 1560 mit dem Titel: "es gibt nicht bloß 36 gute und schlechte unbedingte Syllogismen", wie Aristoteles mit Deutern gelehrt zu haben gesehen wird, sondern 512, von denen allerdings 36 anerkannt würden, die übrigen werden alle verworfen.
Danach bin ich auf desselben "Über dialektische Widersprüche" gestoßen, herausgegeben nach dem Tod des Autors in Basel, im Oktav, im Jahre 1576, wo er in dialektischen Fragesätzen und dem Buch über die ausgezeichneten Regeln aufgestellt hatte, er verteidigt gleichsam wie eine Schutzrede, auf 23 Fragestellungen beruhend; er verspricht dort auch ein Buch über die Möglichkeiten zum Auffinden und Beurteilen, und seine Vorlesungen in einem umfassenden Werk mit einer lateinischen Fassung, die unveröffentlichten Vorlesungen, die ich vielleicht vom Autor wichtiger abgefasst erachte als vollkommenen. Aber wenn es auch nötig ist die Veränderung der Reihenfolge zu behandeln, welche er in der Fragestellung 4 beurteilt, weil aber die wichtigsten Teile von den Verbindungen geschuldet sind, werden wir sie hier darstellen. Als der Titel dessen Buchs über die Verfahren sich zuerst erschienen ist, haben wir ehe wir hinein gesehen haben, haben wir nach unseren mitgeteilten auf diese Weise die Berechnung unterzogen: Das Verfahren ist die Gliederung oder die Form des Syllogismus, durch Überlegung des Umfangs und der Beschaffenheit: Vom Umfang her ist die Darlegung aber entweder allgemeingültig oder gilt nur zum Teil oder ist unbestimmt oder einzigartig; wir werden aus Gründen der Kürze die Anfangsbuchstaben verwenden: U allgemeingültig , P gilt nur zum Teil , I unbestimmt , S einzigartig ; von der Beschaffenheit sind sie entweder bejahend oder bejahend, A bejahend , N verneinend . Ein Syllogismus hat aber 3 Behauptungen, deshalb ist der Syllogismus von der Aussage des Umfangs entweder gleich oder ungleich: 1) der Syllogismus ist so beschaffen: U, U, U. 2. P, P, P. 3. I, I, I. 4. S, S, S, von denen 19 brauchbar sind. 2) der erste und vierte sind ungleich entweder zum Teil oder im Ganzen: zum Teil, wenn jede der beiden Behauptungen vom gleichen Umfang ist, die dritte unterschiedlich.
Und in einem solchen Fall sind zwei Arten des Umfangs im gleichen Syllogismus, wiewohl eine zweimal wiederholt wird, das alles trifft auf verschiedene Art zu, so oft 4 Dinge das ist Arten dieser Umfänge U, P, I, S auf verschiedene Art zusammensetzbar sind nämlich 6Mal, und im einzelnen Fall sind es 2, weil bald dieses zweimal wiederholt wird, bald jenes, im anderen einfach erscheinend; also 6 · 2 macht 12. Und auch wiederum so in einzelnen, das Verhältnis der Anordnung, die Veränderungen sind 3, denn z. B. dieses U, U, P, wird entweder wie so angeordnet, oder so: P. U. U, oder so: U, P, U; also 12 · 3 macht 36. Aus diesen sind brauchbar 18: 2. U(S) U(S) S(U) 2. U(S) S(U) U(S) 2. S(U) U(S) U(S) 4. U(S) U(S) P oder I: 4. U I(P) I(P) oder an Stelle U, S. 4. I(P) U J(P) und S an Stelle U.
Sie sind im Ganzen ungleich, solange keines mit dem anderen aus der gleichen Bedeutung ist, und so geht ein beliebiger Syllogismus 3 Arten ein, so oft wie andere so oft können 4 Dinge zu 4 vereinigt werden, nämlich 4 Mal. Drei aber werden im Verhältnis der Ordnung 6 Mal verändert, z. B. U, P, I; U, I, P; P, U, I; P, I, U; I, U, P; I, P, U. Also 4 · 6 macht 24. Aus denen sind 12 brauchbar. 2: U, P(I.) I(P), 2. I(P) U. P. (I); ebenso viele wenn man für U S setzt. 4 + 4 macht 8. 2. U(S) S (U)P; ebenso viele wenn man für P I setzt. 2 + 2 macht 4. Zählen wir jetzt zusammen: 4 + 36 + 24 macht 64. Diese sind nur die Veränderungen des Umfangs. Von denen sind brauchbar: 2 + 18 + 12 macht 32. Die übrigen fallen unter Regel 1 aus reinen besonderen folgt nichts; 2. Die Schlussfolgerung übertrifft keine von den Prämissen im Umfang, wenn sie auch vielleicht manchmal von beiden übertroffen wird, wie beim Barbari.
Ferner gibt es nur zwei Verschiedenheiten bei der Beschaffenheit, A und N, Behauptungen aber 3, daher bedarf es der Wiederholung, und entweder ist das Verfahren ähnlich, das heißt von derselben Beschaffenheit, oder unterschiedlich: dies ist nichts anderes als Veränderung, weil es niemals i, dem Ganzen, sondern immer in einem Teil unterschiedlich ist, denn niemals sind alle Behauptungen unterschiedlich, weil es nur 2 Verschiedenheiten gibt. Es gibt 2 gleiche Arten: A, A, A; N, N, N; 2 ungleiche: A, A, N oder N, N, A; ungleich wird einzig das Verhältnis der Ordnung 3mal verändert, z. B. A, A, N; N, A, A; A, N, A. Also 2 · 3 macht 6 + 2 macht 8. So oft wird die Beschaffenheit verändert. Von denen sind 3 Veränderungen brauchbar: A A A; N A N; A N N, nach Regel 1 aus den nur verneinenden folgt nichts; 1. Die Schlussfolgerung folgt zum geringeren Teil aus der Beschaffenheit. Aber weil das Verfahren die gleichzeitige Veränderung der Beschaffenheit und des Umfangs ist, und so lassen einzelne Veränderungen des Umfangs einzelne der Beschaffenheit zu, daher 64 · 8 macht 512. Die Anzahl aller brauchbaren und unbrauchbaren Verfahren.Aus diesen findet man die brauchbaren so: multipliziere die brauchbaren Veränderungen des Umfangs mit der Beschaffenheit, 32 · 3 macht 96; vom Produkt ziehe alle Verfahren ab, die im Frisesmo enthalten sind, das ist welche zwar im Verhältnis der Beschaffenheit A, N, N sind, im Verhältnis des Umfangs aber ein Hauptsatz I oder P ist, im Untersatz aber U oder S, und die Schlussfolgerung I oder P, was so viele sind 8. Denn der Frisesmo ist, wenn auch das Verfahren an sich gewissermaßen stockend ist, dennoch in keiner Figur ist, siehe unten, jetzt 96 - 8 macht 88. Die Anzahl brauchbarer Verfahren von Johannes Hospinianus, dem unser Verfahren unbekannt war, ist es anders, aber auf Umwegen gelungen. Zuerst untersucht er deshalb im Kapitel 2 und 3 die 36 aristotelischen Verfahren aus der Verknüpfung U, P, I unter Auslassung von S und der Schlussfolgerung; von denen sind 8 brauchbar UA, PA im Darius und im Datisus, PA, UA im Disamis, UA, UN im Camestres, UN, UA im Celarent, Cesare, Felapton, UA, IN im Baroco, UN, IA in Ferio, Festino, Ferison, IN, UA im Bocardo. Zu denen addiert er im Kapitel 4 einzigartige ähnliche gleichee SA, SA, SN, SN, 2 ungleiche aus drei Arten einzeln umgedreht, und zu beliebigen entweder A oder N z.B. 3 · 2 · 2 macht 12 + 2 macht 14.
Von diesen lässt Johannes Hospinianus nur UA, PA zu und setzt sie in den Darii. Weil einzelne mit teilweise zutreffenden gleich zu setzen sind, sagt er, mit der allgemeinen Lehre der Logik, was wir jedoch bald als falsch zu sein zeigen werden. Im Kapitel 5 fügt Johannes Hospinianus den einzelnen eben so viele ungleiche hinzu, nämlich 14, aus denen Johannes Hospinianus nur SN, UA zulässt in den Bocardo, ebenso UN, SA in den Ferio. In Kapitel 6 zählt er bei zugefügter Schlussfolgerung gleichsam nochmals beginnend die gleichen ähnlichen Verfahren 4 · 2 macht 8, von diesen sind brauchbar nur UA, UA, UA im Barbara, Johannes Hospinianus zufolge ähnliche ungleiche sind entweder aus allen ungleichen, darüber unten, oder zum Teil, von denen nun, wo zwei Behauptungen von demselben Umfang sind, die dritte wie auch immer verschieden; und dann vorausgesetzt dass nur zwei allgemein gültig sind, eine unbestimmt, in welchem Falle die Verfahren 6 sind (denn eine wird entweder an den Anfang, oder in die Mitte, oder ans Ende gesetzt 3, und immer sind entweder alle A oder N 3 · 2 macht 6) oder im Gegenteil sind es auch 6 nach Kapitel 7 macht 12. Aus den vorhergehenden ist nur 6 brauchbar UA, IA, IA im Darii und Datisi, ebenso IA, UA, IA im Disamis, ebenso UA, UA, IA im Darapti, und wie Johannes Hospinianus nicht unpassend sagt, im Barbari. Gewiss weil aus der Behauptung UA zwei PU folgen, eine umgekehrt, entsteht hier ein Verfahren des mittelbaren Baralip; abwechselnd mit der untergeordneten 1 z. B. Alle Tiere sind körperlich. Alle Menschen sind Tiere. Also Irgendein Mensch ist körperlich. Daher entsteht dieser Barbari. Eben so viele, nämlich 12, Verfahren gibt es durch den Katipel 8, wenn zwei U und ein P verknüpft werden, oder umgekehrt; und diese sind brauchbare Verfahren, die in der nächsten Mischung sind, wenn man für I P setzt. Eben so viele, nämlich 12, Verfahren gibt es nach Kapitel 8, wenn zwei U und ein S nach Kapitel 9 verbunden werden, und weil Johannes Hospinianus S für P hat, glaubt er es gibt nur ein brauchbares Verfahren im Darii UA, SA, SA, siehe unten. Ebenso 12 IIP oder PPI alle unbrauchbar nach Kapitel 10. Ebenso 12 IIS oder SII, alle, wie von ihm geglaubt wird, unbrauchbare nach Kapitel 11. Ebenso 12 PPS oder SSP, alle, wie von ihm geglaubt wird, unbrauchbare nach Kapitel 12. Nun macht 6 · 12 macht 72 + 8 macht 80, die Anzahl der ähnlichen Verfahren zu den zugefügten Veränderungen der Schlussfolgerung. Unähnliche Verfahren sind entweder gleich oder ungleiche. Gleiche sind aus nur entweder U oder P oder I oder S, 4 Arten die durch das Verhältnis der Beschaffenheit so verändert werden: NNA, ANN usw. 6mal, wie wir vorher gesagt haben Nr. 20 nun 6 · 4 macht 24, siehe Kapitel 13 brauchbar ist: UA, UN, UN im Camestres.
Unähnliche ungleiche sind entweder aus allen ungleichen, weil keine Behauptung anders ist als gleich, darüber unten, oder aus einem Teil, wie zwei gleich seien, eine ungleich, dazu jetzt. Und wir haben gesagt alle Veränderungen des Umfangs gehen zurück, über diese in ähnlichen aus Kapiteln 7, 8, 9, 10, 11, 12 auf einzelne von beiden gegensätzlichen; die Verfahren aber bewirken hier mehr als dort, wegen der hinzukommenden Veränderung der Beschaffenheit. Es war daher im Kapitel 7 UUI oder umgekehrt IIU. Die Anordnung des Umfangs wird 3mal verändert, weil z. B. I alsbald am Anfang, alsbald in der Mitte alsbald am Ende gesetzt wird.Ferner wird die Verknüpfung der Beschaffenheit sowohl 2mal verändert, NNA oder AAN, als auch die Reihenfolge 3mal wie oben gesagt, das Setzen von A oder N an den Anfang oder die Mitte oder das Ende, also3 · 2 · 3 macht 18 von UUI, und dagegen auch 18 von IIU macht 36 nach Kapitel 14. Die vorigen 18 brauchbaren haben die Verfahren: UA, UN, IN; oder anstelle IN, PN oder SN, und sie sind nach Art des Camestres, wie oben der Barbari; UN, I(PS)A, I(PS)N in Ferio, Festino und Ferison, der jedoch zuletzt keinen Platz in S hat; I(PS)N, UA, I(PS)N im Bocardo. Ähnlich haben UUP oder PPU 36 Verfahren. Die brauchbaren haben wir kurz zuvor durch P in () bezeichnet. Ähnlich machen UUS oder SSU ebenfalls 36 Verfahren nach Kapitel 15. Die brauchbaren Verfahren haben wir im vorigen mit S gekennzeichnet. IIP oder PPI machen genauso 36 nach Kapitel 16, die Verfahren sind alle unbrauchbar. IIS und SSI und PPS und SSP machen 2 · 36 = 72 Verfahren nach Kapitel 17, die alle unbrauchbar sind. Hierhin haben wir immer wieder die ungleichen verschoben aus dem Ganzen, wo keine Behauptung im selben Syllogismus vom gleichen Umfang ist, sie sind aber entweder ähnlich oder unähnlich; die ungleichen aus den ganzen gleichen sind: UIP, deren Form 12 Verfahren hat, denn 3 Dinge verändern ihre Anordnung 6mal, die Beschaffenheit aber wird 2mal verändert; also 6 · 2 macht 12 nach Kapitel 18, wo die unbrauchbaren sind: UA, I(PS)A, P(IS)A, UA, P(IS)A, I(PS)A im Darii und Datisi; I(PS)A, UA, P(IS)A, P(IS)A, UA, I(PS)A im Disamis, außer was den Untersatz in der dritten Form nicht mit S beginnt; UPS und UIS, die 24 Verfahren haben nach Kapitel 10. Die brauchbaren haben wir vorher durch S gekennzeichnet. IPS, welche 12 Verfahren hat nach Kapitel 20; aber alle sind gemäß Johannes Hospinianus unbrauchbare.
Die unähnlichen sind insgesamt ungleich durch dasselbe Verfahren, wie die gleichen: UIP welches die Anordnung 6mal verändern, die Beschaffenheit aber verändern sie 6mal; also 6 · 6 macht 36 nach Kapitel 21. Brauchbare Verfahren sind: UA, I(PS)N,P(IS)N im Baroco; UN, I(PS)A, P(IS)N im Ferio, Festino und Ferison. I(PS)N, UA, P(IS)N im Bocardo. UIS und UPS. 36 · 2 macht 72 nach Kapitel 22. Brauchbare Verfahren haben wir vorher durch S und P und I in () gekennzeichnet. IPS hat 36 Verfahren nach Kapitel 23, alle unbrauchbar gemäß der Lehre von Johannes Hospinianus. Zählen wir nun alle berechneten Verfahren von Kapitel 6 bis einschließlich 23 zusammen (denn die vorhergehenden sind auf diese zurückgegangen) 80 + 24 + 36 + 36 + 36 + 36 + 72 + 12 + 24 + 12 + 36 + 72 + 36. Oder 80 + 12 · 36 macht 512. Von diesen Betrachtungen des Johannes Hospinianus loben wir einige, einige wünschen wir uns. Wir loben die Erfindung neuer Verfahren: Barbari, Camestres, Celaro, Cesaro; wir loben was er richtig erkannt hat, Verfahren, für die sie gewöhnlich Namen erfunden haben, z. B. Darii u. s. w. halten sich für unzählige Verfahren gleichsam Abstammung zur Art, denn unter Darii ist enthalten dieser neue aus dessen Annahme: UA, IA, IA; UA, SA, SA; UA, PA, PA; UA, IA,SA; UA, SA, IA; UA, JA, PA; UA, PA, IA; UA, SA, PA; UA, PA, SA. Aber wir können es nicht auf gleiche Weise prüfen, weil er einzelne vergleicht mit besonderen, welche Sache alle seine Überlegungen verwirrt, und bewirkt seine brauchbaren Verfahren nur wenig richtig, wie bald ersichtlich wird. Hier bekennt er selbst i, Kapitel 22 Seite 430 in "Über den Streit der Dialektiker" sich zu irren und er lässt 38 brauchbare Verfahren zu, nämlich 2 mehr als die vorigen 36. 1. Im Darapti, weil aus nur UA SA geschlossen wird, weil ja Christus so geschlossen hätte Lukas 23, Verse 37, 38; 2. im Felapton, weil aus UN und UA geschlossen wird, SN weil Paulus Römer 9, Vers 13 geschlossen hat. Wenn wir auch erkennen so wird es gewöhnlich verstanden, erachten wir alle anderen für wahrer. Nämlich diesen: Sokrates ist der Sohn des Sophroniskos von Alopeke, wenn es aufgelöst wird etwas gemäß des Verfahrens von Johann Raue, wird man es so haben: Wer auch immer Sokrates ist, ist der Sohn des Sophroniskos von Alopeke. Und es wird nicht schlecht gesagt: Jeder Sokrates ist der Sohn des Sophroniskos von Alopeke, wenn er auch der einzige wäre, (denn wir sprechen nicht vom Namen, sondern über jenen Menschen) ähnlich wie wenn ich sagte: Dem Titius gebe ich alle Kleider, die ich habe, ich vermache sie, wenn ich auch ein einziges hätte, wer bezweifelt es ist ihm geschuldet? Allerdings verweilt er den Rechtsberatern zufolge an der Universität in einer I. Stadt 7. D. weil allgemein der hochgeschätzte Name August Benedict Carpzov Seite 11, Kapitel VI, Definition 17. Denn der Ausspruch: alles, verursacht nicht die Vielzahl sondern das Verständnis einzelner. Allerdings unterstellt Sokrates hätte keinen Vater gehabt, sage ich so richtig: Der Sohn aller Sophroniskos von Alopeke ist Sokrates. Was wir über diese Behauptung sagen werden: Ist dieser Mensch gelehrt? Woraus wir richtig schließen werden: Petrus ist dieser Mensch, also ist Petrus gelehrt. Der Ausdruck dieser ist aber eine einzigartige Bezeichnung. Deshalb hören wir allgemein sagen: jede einzigartige Behauptung ist im Verhältnis des Verfahrens im Syllogismus für das allgemeine zu halten, ebenso jede unbestimmte für eine den Teil betreffende. Daher zählt er indes nur 36 brauchbare Verfahren, es sind jedoch 88, darüber oben, nichtsdestoweniger unter Auslassung von Veränderungen die aus der Figur entstehen. Denn die zu verschiedenen Figuren gehörenden Verfahren, das ist die zum Umfang und der Beschaffenheit gehörigen, sind einfach eines, z. B. Darii und Datisi. Die einfachen Verfahren aber benenne ich, nicht durch berechnete Veränderung der Figuren, die Geformten dagegen sind solche Verfahren der Figuren, welche sie gewöhnlich zählen. Handle also, dass nicht was unvollständig wäre, und zu dem wir herabstiegen solange der Schwung währte. Für die Figur werden drei Begriffe gefordert: der Vordersatz, den wir mit dem griechischen μ Vordersatz, den Untersatz den wir mit dem lateinischen M Untersatz bezeichnen werden, dem Mittleren mit dem deutschen 𝔐 Mittelbegriff, und einzelne zweimal. Daraus werden 3 Verknüpfungen von 2 gemacht, die hier Behauptungen genannt werden, deren letzte die Schlussfolgerung ist, die vorigen Prämissen. Die allgemeinen Regeln um jede Figur von 2 zusammenzustellen sind: 1. niemals werden zwei gleiche Begriffe von zusammengestellt, denn keine Behauptung ist MM oder Untersatz Untersatz. 2. M Untersatz und 𝔐 Mittelbegriff werden ausschließlich in der Schlussfolgerung zusammengestelltgestellt, so dass immer M vorangestellt wird nach der Methode M𝔐. 3. in den Prämissen werden in der 𝔐 und M zusammengestellt, in der zweiten M und μ.Denn ich halte es nicht für eine Veränderung der Figur, jedes mal wenn irgendwer die Prämissen umstellen, und anstelle dessen: B ist C, A ist B, also A ist C, stellen sie so: A ist B, B ist C, also A ist C, wie Petrus Ramus, Pierre Gassendi es anordnen, ich weiß nicht welcher J. C. E. das sonderbare Büchlein herausgegeben hat, und schon seit Alkinoos stellen sie immer den Obersatz nach, den Untersatz vor. Aber das verändert nicht die Figur, im Übrigen wären so viele Figuren, wie die Rhetoriker als Veränderungen zählen, solange im gewöhnlichen Leben die Schlussfolgerung bald am Anfang, bald in der Mitte, bald am Ende welche sie beachten.
Es ist somit offensichtlich, dass die Veränderung der Figuren aus der Anordnung des Mittelbegriffs in den Prämissen entsteht, wenn sie nur dem Vordersatz vorangestellt wird, dem Untersatz nachgestellt wird, welche das I. aristotelische Verfahren ist, im Vorder- und Untersatz nachgestellt, welches das II. aristotelische Verfahren ist, beiden vorangestellt, welches das III. ist, dem Vordersatz nachgestellt, dem Untersatz vorangestellt, welches das IV. des Galenos von Pergamon ist (irrtümlich von Johannes Hospinianus in " De Controversiis dialecticis" Fragestellung 19 dem Johannes Duns Scotus zugeschrieben, weil dieser ihn an Averroës erinnert hätte) was Thomas Hobbes bestätigt in "Erster Teil der Grundlagen der Philosophie über Körper" Kapitel 4, Abschnitt 11 bestätigt. Sie werden so bezeichnet werden: I. 𝔐 Mittelbegriffμ Vordersatz·M Untersatz𝔐 Mittelbegriff, M Untersatzμ Vordersatz, II. μ VordersatzM Untersatz, M Untersatz𝔐 Mittelbegriff, M Untersatzμ Vordersatz III. 𝔐 Mittelbegriffμ Vordersatz, 𝔐 MittelbegriffM Untersatz, M Untersatzμ Vordersatz. IV. μ Vordersatz𝔐 Mittelbegriff, 𝔐 MittelbegriffM Untersatz, M Untersatzμ Vordersatz. Der IV. Figur widerspreche ich inzwischen mit Gegnern in einem: Die vierte Figur ist genau so gut wie die erste selbst; allerdings wenn nur nicht des Prädikats, wie man allgemein gewohnt ist, sondern des Subjekts, wie Aristoteles wir diejenige aussagten, aus IV wird I gemacht und umgekehrt. Denn Aristoteles ist gewohnt diese z. B. die Behauptung: alles α ist β als alles β ist in α enthalten auszusprechen. Die Bezeichnung der vierten Figur entsteht so: 𝔐 Mittelbegriff ist dann enthalten in μ Vordersatz, M Untersatz, ist dann enthalten in 𝔐 Mittelbegriff, also M Untersatz ist μ Vordersatz; oder wie die Schlussfolgerung auch so ausgedrückt wird, die umzustellenden Vordersätze und die Schlussfolgerung wird sein: Also μ Vordersatz ist dann in M Untersatz enthalten. Dasselbe kann mit anderen Figuren gemacht werden, welches Kunststück bisher niemand beachtet hat.
Im übrigen entsteht die zweite aus der ersten, aus umgestellten Obersätzen; die dritte durch umgestellte Untersätze; die vierten aus umgestellter Schlussfolgerung, aber hier wird ein anderer Syllogismus erzeugt, weil es eine andere Schlussfolgerung ist. So dass dessen vierte Verfahren als mittelbare Verfahren der ersten Figur zu bezeichnen sind wie sie gewöhnlich genannte werden, wenn man nur den Vordersatz dem Untersatz voranstellt, nicht umgekehrt, dass allein wegen dieses Grundes gewöhnlich gegen den Brauch aller dieser Figuren, dass die vierte des Galenos von Pergamon vermieden würde, Tatsache ist, z. B. es sei der Syllogismus im Baralip: jedes Tier ist ein Wesen, jeder Mensch ist ein Tier, also jedes Wesen ist ein Mensch. Sicher ist Wesen ein untergeordneter Begriff, deshalb ist die Prämisse in die er eingefügt wird, eine nachgeordnete, und als Folge ist die Behauptung diese: Jedes Tier ist ein Wesen, sie kann nicht vom ersten auf den zweiten Platz gesetzt werden, dann wird ganz leibhaftig die vierte Figur hervorgehen.
Wegen dieser Umstellung der Behauptungen, welche die Syllogismen gewöhnlich in den Celantes setzen, sind sie im Fapesmo, anstelle von Frisesmo ist Fresismo zu sagen, anstelle von Datibis Ditabis; Baralip bleibt. Das sind die Verfahren der vierten Figur, denen ich Celanito und Colanto zufüge. Es werden zugleich 6 Verfahren sein: die ersten sind 6: Barbara, Celarent, Darii, Ferio, Barbari, Celaro; die zweiten 6 Verfahren: Cesare, Camestres, Festino, Baroco, Cesaro, Camestres; die dritten Verfahren ebenfalls 6: Darapti, Felapton, Disamis, Datisi, Bocardo, Ferison. So wird ein bisher unbekannter Gleichklang der Figuren entdeckt, denn einzelne Verfahren sind gleichwertig. 1) in der erste und der zweite Figur ist aber immer ein Vordersatz U allgemeingültig ; 2) die erste und dritte ist immer ein Untersatz A bejahend ; 3) in der zweiten ist die Schlussfolgerung immer N verneinend ; 4) in der dritten ist die Schlussfolgerung immer P gilt nur zum Teil ; in der vierten ist die Schlussfolgerung niemals U allgemeingültig A bejahend , im Hauptsatz niemals P gilt nur zum Teil N verneinend , und wenn der Untersatz N verneinend ist, ist der Obersatz U allgemeingültig A bejahend . Infolge dieser Regeln wird gemacht, dass nicht jede beliebiger der 88 brauchbaren Verfahren in jeder beliebigen Figur ihren Platz hat; ohnehin wären die brauchbaren Verfahren 4&nbsP,· 96 macht 348. Die Verfahren aber werden in der brauchbaren und unbrauchbaren Welt gebildet 512 · 4 macht 2048. Welche aber in welcher Figur brauchbar sind lehrt das gegenwärtige Schema:
0 4 3 2 1 8 UA, UA, UA. SA, SA, SA. UA, UA, SA. UA, SA, UA. SA, UA, UA. SA, SA, UA. SA, UA, SA. GA. SA, SA. 1 … — — — Barbara. 8 UN, UA, UN. SN, SA, SN. UN, UA, SN. UN, SA, UN. SN, UA, UN. SN, SA, UN. SN, UA, SN. UN, SA, SN. 2 … — — Cesare. Celarent. 8 UA, UN, UN. SA, SN, SN. UA, UN, SN. UA, SN, UN. SA, UN, UN. SA, SN, UN. SA, UN, SN. UA, SN, SN. 3 … — — Camestres. — 8 UA, UA, PA. UA, UA, IA. SA, SA, PA. SA, SA, IA. UA, SA, IA. UA, SA, PA. SA, UA, IA. SA, UA, PA. 4 … Baralip. Darapti. — Barbari 8 UN, UA, PN. UN, UA, IN. SN, SA, PN. SN, SA, IN. UN, SA, IN. UN, SA, PN. SN, UA, IA. SN, UA, PN. 5 … Celanto. Felapt. Cesare. Celaro. 8 UA, UN, PN. UA, UN, IN. SA, SN, PN. SA, SN, IN. UA, SN, IN. UA, SN, PN. SA, UN, IN. SA, UN, PN. 6 … Fapesmo. — Camestres. — 8 UA, IA, IA. UA. PA, PA. UA, PA, IA. UA, IA, PA. SA, IA, IA. SA, PA, PA. SA, PA, IA. SA, IA, PA. 7 … — Datisi. — Darii. 8 UN, IA, IN. UN, PA, PN. UN, PA, IN. UN, IA, PN. SN, IA, IN. SA, PA, PN. SN, PA, IN. SN, IA, PN. 8 … Fresismo. Ferison. Festino. Ferio. 8 UA, IN, IN. UA, PN, PN. UA, PN, IN. UA, IN, PN. SA, IN, IN. SA, PN, PN. SA, PN, IN. SA, IN, PN. 9 … — — Baroco. — 8 IA, UA, IA. PA, UA, PA. IA, UA, PA. PA, PA, UA. IA, SA, IA. PA, SA, PA. IA, SA, PA. PA, SA, IA. 10 … Ditabis. Disamis. — — 8 IN, UA, IN. PN, UA, PN. IN, UA, PN. PN, PA, UN. IN, SA, IN. PN, SA, PN. IN, SA, PN. PN, SA, IN. 11 … Colanto. Bocardo. — — Es verbleibt 8 IA, UN, IN. PA, UN, PN. IA, UN, PN. PA, UN, IN. IA, SN, IN. PA, SN, PN. IA, SN, PN. PA, SN, IN. 12 Frisesmo. — — — In der [Tabelle] sind alle brauchbaren Verfahren beschrieben, aus denen acht immer ein allgemeines Bildungsverfahren darstellen, solche aber nenne ich jene gewöhnlich benannten, in denen U und S, ebenso I und P für ein und dasselbe gehalten werden: Die Zeilen der Verfahren selbst bestehen aus vier Gruppen von Dreien, in jeder der Zeilen stimmen im Umfang überein, unterscheiden sich für drei jener brauchbaren durch die Unterschiede der Beschaffenheit. Aber die Dreiergruppen unterscheiden sich untereinander durch den Umfang, in die Reihenfolge gestellt die wir über die Veränderungen finden, auf deren vier alle vorher gefundenen zurückgeführt werden, weil hier U und S, ebenso I und P zurückgeführt werden auf dieselben. An den Rand einer beliebigen Zeile haben wir die gebildeten allgemeinen Verfahren gestellt, in deren besonderes Verfahren es fällt. In der obersten haben wir die Nummer der Figur bezeichnet.
Daraus wird aber offensichtlich, dass die gebildeten Verfahren allgemein sind entweder einzige oder entsprechende, und diese entweder 2 oder 3 oder 4, je nachdem mehre oder weniger einer Zeile sind entgegengesetzte. Einzelne der Zeilen haben weiterhin ein einfaches allgemeines Verfahren, das wir durch Anwendung von Vokalen erklären können, wie gewöhnlich, wenn A sei UA (oder SA), E sei UN (oder SN), I sei P (oder I)A, O sei P(I)N (so werden außerdem 4 Vokale ausgelassen U für IA, Y für IN, OY oder sein SA, ω für SN; welche zur Erklärung von Johannes Hospinianus Johann Regius gesetzt hat, siehe "Commentariorum Ac Disputationum Logicarum" Buch 4 Fragestellung 5), und so ist das Verfahren der Zeile 1 AAA, 2. EAE. 3. AEE, 4. AAI, 5. EAO, 6. AEO, 7. AII, 8. EIO, 9. AOO, 10, IAI, 11, AEE, 12. IEO, durch die verworfenen Konsonanten nämlich aus den gewöhnlichen Sprachen, in denen die Scholastiker durch geeignete Figur, durch Vokale einfache Verfahren bezeichnet haben. Aber das letzte Verfahren: IEO, das wir Fresesmo genannt haben, und in die Nullte Figur angeordnet haben, ist deswegen unbrauchbar, weil der Oberbegriff P ist (daher hat er keinen Platz in 1 und 2), der Unterbegriff aber N (daher hat er keinen Platz in 1 und 3), wenn er auch nach den Regeln der Verfahren nicht unbrauchbar wäre. Was aber in den 4 keinen Platz hat, zeige ich mit dem Beispiel: Ein gewisses Seiendes ist ein Mensch, kein Mensch ist dumm, also ist ein gewisses Dummes kein Seiendes.
Und auch hier werde ich beiläufig einen brauchbaren Rat zur Verfügung stellen, der und sogar durch dieses Beispiel bewiesen wird, auf dem der Beweis beruht, wenn ich so sagen will, oder eine Kunst das vorgeschlagene Verfahren zu prüfen, und wo immer nicht die Formen, sondern durch die Kraft des Stoffs schließt er, gegenwärtig schneller zu finden ist, wie bei den Logikern insofern zu lesen ich mich nicht erinnere. In Kürze: Für UA wird die Behauptung genommen, die nicht erlaubt die Materie einfach umzuwandeln, z- B. wird dies besser genommen: Jeder Mensch ist ein Tier, als: Jeder Mensch ist ein verständiges Tier, und damit wird eine entlegenere Art genommen, dies wird man für genauer halten. Für UN würden ein solche ausgewählt, welche Art voneinander verneint würde wie besonders zueinander benachbarte unter derselben nächsten Art, z. B. der Mensch ist eine Bestie, und die nicht durch Umkehrung in UA umwandelbar sei oder deren unbegrenzter Begriff weder ein Subjekt noch ein Merkmal wäre. Für P(I)A wird immer genommen ein solches, das nicht ein Unterbegriff irgendeines UA wäre, sondern in dem von der Art wie die besondere Gattung äußerst allgemein gesprochen wird. Für (I)PN wird genommen, was nicht irgendeinem UN nachgeordnet ist, und dessen unbegrenzter Begriff keiner von beiden ist, und in dem die Gattung von der Art am weitesten entfernt verneint wird.
Was wir über das Vermeiden von unbegrenzten Begriffen gesagt haben, deren Überlegung wird jetzt offensichtlich werden. Es ist hervor gegangen eines gewissen Johann Christoph Sturm "Zusammenstellung der Allgemeinbegriffe oder der euklidischen Metaphysik", herausgegeben in Oktav in Den Haag im Jahre 1660 (1661) bei Adriaan Vlacq. Dem er von ihm dargelegte neue syllogistische Verfahren angehängt hat, die alle entsprechend der üblichen Lehre in der einen oder beiden der beiden Regeln der Bedeutung anzustoßen scheinen. Aus rein negativen folgt nichts; und: die Schlussfolgerung folgt der Bedeutung aus der schwächeren Prämisse. Denn dass das Argument richtig fortschreitet, oder die bejahende unbegrenzte Behauptung des Gegenstands annimmt, der für eine begrenzte Negative stünde, oder umgekehrt, z. B. sind sie gleichbedeutend. Irgendein kein Stein ist ein Mensch, und irgendein Stein ist kein Mensch (aber ich merke an, dass in umfassendem Gegenteil nicht fortzufahren ist, z. B. jeder Stein ist kein Mensch, also ist alles, was kein Stein ist, ein Mensch); entweder nähme er eine Verneinende des unbegrenzten Prädikats an für das bejahende begrenzte oder das Gegenteil, z. B. sind sie gleichbedeutend: jeder Philosoph ist nicht kein Mensch, und: er ist ein Mensch; oder 3. Oder er nimmt anstelle des gegebenen das umgekehrte als dessen Umkehrung. Nun wird UA durch Umkehrung umgewandelt in UN, U und PN in PA, so ist es einfach aus rein negativem das Bejahende hervorzubringen, wenn dessen Verneinungen so beschaffen sind, dass sie für das Bejahende stehen; ebenso aus A und N das Bejahende hervorzubringen, wenn diese für das Negative stünden. So ist offensichtlich, alle jene 8 Veränderungen der Beschaffenheit brauchbar sein werden, und als Folge werden die brauchbaren Verfahren 32 · 8 macht 256 sein nach unserer Berechnung. Ähnlich wird die Überlegung zu dessen Syllogismus sein, über den die Logiker streiten: Wer auch immer nicht glaubt, wird verdammt, Die Juden glauben nicht, also werden sie verdammt. Aber dessen Lösung ist vorschnell, der Untersatz ist bejahend, weil der mittlere Begriff bejaht wird vom nachfolgenden. Der mittlere Begriff aber ist nicht: zu glauben, sondern: nicht zu glauben, denn das ist im Obersatz vorhanden gewesen. Ich kann hier nicht das Verfahren Darapti aus der geistreichen Erfindung unseres berühmten Jakob Thomasius übergehen. Dieser hat erkannt aus Petrus Ramus "Scholae Dialecticae" Buch 7, Kapitel 6 Seite 214 Marginalie, die Umwandlung kann im Syllogismus gezeigt werden durch Hinzufügen der gleichen Behauptung, z. B. UA in PA so: jedes α ist γ, jedes α ist α (wenn man im 3. Verfahren des Darapti, oder jedes γ ist γ, wenn im 4. Verfahren des Baralip), also ein gewisses γ ist α. Ebenso PA in PA so: ein gewisses α ist γ, jedes α ist α (wenn man im 3. Verfahren des Disamis will, oder jedes γ ist γ, wenn im 4. Verfahren des Ditabis), also ein gewisses γ ist α. Ebenso UN in UN (im 2. Cesare) so: Kein α ist γ, jedes γ ist β, also ist kein γ ein α. Ebenso PN entweder im 3. Baroco so: jedes α ist α, ein gewisses α ist nicht γ, also ein gewisses γ ist nicht α (oder im 4. Colanto: ein gewisses α, ist nicht γ, jedes γ ist γ, also ein gewisses γ ist kein α.) Ebenso hat er sich deshalb in der Umwandlung durch Umkehrung versucht, z. B. dessen PN: irgendein Mensch ist nicht gelehrt, in dieser PA des unbegrenzten Subjekts: ein gewisses nicht gelehrtes ist ein Mensch. Der Syllogismus im Darapti wird so beschaffen sein: Jeder Mensch ist ein Mensch, ein gewisser Mensch ist nicht gelehrt, also ein gewisser der nicht gelehrt ist, ist ein Mensch. Zwei Dinge müssen hier jedoch beachtet werden, der Untersatz wird gemäß der Lehre von Johann Christoph Sturm gewissermaßen als anderes gesetzt gelten: ein gewisser Mensch ist nicht gelehrt; darauf wird alles besser so gesagt: dessen Behauptung: Irgendein Mensch ist nicht gelehrt, umgewandelt durch Umkehrung ins verneinende ist sie auch passend: ein gewisses nicht gelehrtes ist nicht kein Mensch, und durch Umwandlung durch Umkehrung muss die umgekehrte identische sein, das zeigt der Syllogismus nun nicht so sehr im Darapti, sondern im Baroco: Jeder Mensch ist nicht kein Mensch (das ist: jeder Mensch ist ein Mensch), ein gewisser Mensch ist nicht gelehrt, also was nicht gelehrt ist ist nicht kein Mensch (das ist ein gewisses nicht gelehrtes ist ein Mensch).
Übrigens meine ich, dass jene Verfahren von Johann Christoph Sturm nicht durch Überlegung der Form, sondern der Bedeutung schließen, weil was entweder begrenzte oder unbegrenzte Begriffe wären, sich nicht auf die Form der Behauptung oder die Verbindung oder die Bezeichnung bezieht, sondern auf die Begriffe. Wir werden endlich aufhören mit den Verfahren, denn wenn wir auch hoffen wenigstens die gewöhnlichen angeführt zu haben, denn es hat auch die Neuheit in sich den Verdruss. Vom Vorhaben aber abgelassen zu haben wird mancher sagen, der alles aus der vertrauten Lehre der Veränderungen die ich erforscht habe gesehen hätte, die fast einzig durch alles unbegrenzte gehorchenden sich den Sinn ableitet, und die Harmonie der Welt und den innersten Aufbau der Dinge und die Folge der Formen versteht, dessen unglaublicher Nutzen endlich durch die vollkommene Philosophie, oder nahezu vollkommene richtig beurteilt werden wird.
-
Der 7. Gebrauch ist nämlich bei zu verschränkenden geometrischen Figuren, in welcher Angelegenheit Johannes Kepler das Eis in 2. Buch der "Fünf Bücher der Harmonie der Welt" gebrochen hat. Durch diese Verknüpfungen kann nicht nur durch neue grenzenlose Lehrsätze die Geometrie bereichert werden, denn die neue Verknüpfung erzeugt eine neue zusammengesetzte Figur, deren nun zu betrachtenden Eigenschaften, erstellen wir neue Theoreme, wir denken uns neue Beweise aus, aber auch (wenn es freilich wahr ist, dass bedeutendes aus geringem zusammengesetzt wird, sei es dass man dieses Atome oder Moleküle nennt) ist es der einzige Weg in die Geheimnisse der Natur einzudringen, weil durch diese gesagt wird, dass jeder einzelne die vollkommenere Sache erkennt, durch die Teile der großen Sache und Teile der Teile, er deren Figuren und Stellungen verstanden hat. Diese Erwägung der Figuren ist zuerst gegenstandslos in der Geometrie oder Stereometrie zu erforschen: von da an, wenn man sich der Naturwissenschaft und dem Dasein zuwendet, oder das, was wirklich in den Körpern gefunden wird, wird offenbar die Tür der Physik weit, und das Aussehen der Bestandteile, und der Ursprung und die Mischung der Eigenschaften und der Ursprung der Mischung und die Mischung der Mischungen, alles was uns bisher an der Natur rätselhaft erschien.
Was das betrifft werden wir einen kurzen Vorgeschmack geben, durch die wir vieles verstehen würden: jede einfache Figur ist entweder geradlinig oder gekrümmt. Denn alle symmetrischen Geradlinigen, sind gemeinsam Grundlage aller: das Dreieck. Aus dessen verschiedenen passenden Verknüpfungen entstehen alle zusammentretenden geradlinigen Figuren (das ist die nicht lückenhaften = geschlossenen Figuren). Aber von den Kurven kann weder der Kreis in ein Oval u. s. w. noch umgekehrt überführt werden, auch nicht zu etwas gemeinsamen. Keines der beiden aber ist einem Dreieck und zusammengesetzten Dreiecken symmetrisch. Weiterhin ist ein beliebiger Kreis zu irgendeinem Kreis symmetrisch, denn ein beliebiger kann irgendeinem konzentrisch zu sein verstanden werden; Das Oval aber oder die Ellipse sind diesen symmetrisch welche konzentrisch verstanden werden; so ist auch jedes Oval nicht dem Oval symmetrisch usw. Das zu den einfachen; nun zu den Verknüpfungen. Die Verknüpfung ist entweder deckungsgleich oder lückenhaft; übereinstimmend dann, weil die äußeren Linien der zusammengesetzten Figuren oder die Umfänge niemals einen äußeren Winkel bilden, sondern immer einen inneren. Äußerlich aber wird ein Winkel gebildet, indem ein Bruchteil des Kreises zwischen die gezogenen Linien des Winkels beschrieben aus dem Schnittpunkt gleichwie dem Mittelpunkt, er fällt außerhalb der Figur, zu deren Umfang die den Winkel bildenden Linien gehören: innerhalb, weil innen. Nicht geschlossen ist eine Verknüpfung, wenn irgendein Winkel außerhalb gebildet wird. Bei Sternbildern aber ist die Verknüpfung eine offene, alle deren Radien (das ist die Linie die die Sternbilder umgibt den äußeren Winkel bildend) sind gleich, so dass wenn es einem Kreis eingeschrieben wird, er über all diesen Radius berührt. Übrigens nenne ich die offenen Verknüpfung der Figuren Geflechte, besonders die kongruenten Figuren. Denn es gibt sowohl einige gebildete Geflechte, als auch offene Figuren die ich zum Gegensatz zusammentretende nenne.
Nun gibt es die Lehrsätze:
- Wenn zwei unsymmetrische Figuren sich berühren wird (denn die Verknüpfung ist entweder eine unmittelbare Berührung, oder eine mittelbare, zwischen dem dritten und dem ersten, jedes mal ist das dritte mit dem zweiten verbunden, und das zweite entweder mittelbar oder unmittelbar mit dem ersten), eine offene Verknüpfung bewirkt.
- Die Berührung aller Kurven untereinander ist offen, außer die eine wird mit einer Bereich anderer Symmetrie zur gegebenen konzentrisch umgeben.
- Jede Berührung der Kurven mit Geraden ist offen, außer die Geraden werden in die Mitte des Bereichs gelegt. Den Bereich aber nenne ich den Rest in der Figur der größeren Kurve, ausgenommen die konzentrische der kleineren. Bei der Berührung der Geraden wird aber entweder der Winkel vom Winkel, oder der Winkel der Linie eingesetzt.
- Wenn der Winkel dem Winkel einbeschrieben wird oder der Linie, ist die Berührung in einem Punkt.
- Die offene Berührung aller Kurven untereinander ist in einem Punkt.
- In gleicher Weise ist die Berührung aller derer mit einer Geraden auch nicht offen.
- Eine Linie kann nur mit einer Linie der gleichen Art überlagert werden, z. B. eine Gerade mit einer Geraden, eine Kurve mit der gleichen Art und des gleichen Abschnitts.
- Wenn eine Linie mit einer gleichen überlagert wird, ist die Berührung geschlossen, wenn sie ungleich ist, offen.
Es ist aber zu beachten, dass viele Figuren an einem Punkt ihrer Winkel zusammengesetzt werden können, das Geflecht aller ist äußerst offen. Aber deshalb kann auch gemacht werden, dass zwei oder mehr Berührungen offen wären, eine dritte oder mehrere kämen hinzu, und erzeugte eine Figur, oder geschlossene Verknüpfung. So dass eine neue Betrachtung entsteht, welche Figur oder Geflecht durch welche Zugabe aus dem Geflecht eine Figur machen würde, was verstanden zu haben von großer Bedeutung ist für die zu vollendende Öffnung der Dinge. Es verbleibt, dass wir aus unseren Anweisungen aufstellen, zu der erforderlich ist dass die Anzahl der Figuren bestimmt wird zum vollendeten Geflecht, und die zu verknüpfenden Figuren bestimmt werden; denn jede der beiden anderen ist unendlich. Aber das ist jedem beliebigen leicht gemäß der abgezählten Fälle und Lehrsätze zu zeigen; uns reicht es für andere eilende eine Skizze gezogen zu haben zur Behandlung der bisher gewöhnlich vernachlässigten Geflechte. Es geziemte sich vielleicht diese Lehrmeinung durch Schemata zu veranschaulichen, aber die Verstehenden werden es nicht benötigen; die Unerfahrenen, wenn dieser Fall eintritt, werden so viel zu verstehen nicht beurteilen.
-
Der achte Gebrauch ist bei den Rechtsberatern in der Fallgestaltung. Denn nicht immer ist ausschließlich auf den Gesetzgeber zu warten, wenn nur ein Fall auftauchte, und es ist besser sich auf die Gesetze der Klugheit zu verlassen so sehr als möglich am Anfang ohne Fehler zu setzen, als auf die Einschränkung und Richtigstellung des Glücks. Selbst wenn ich verschwiege, dass die Rechtslage in einem beliebigen Staat deshalb besser ist, wo sie weniger im Ermessen des Richters liegt. Platon im Buch 9 über die Gesetze, Aristoteles Buch I über Rhetorik, Giacomo Menochio "Über die willkürlichen Fragen und Fälle der Richter" Buch 1 Vorwort Nr. 1.
Ferner wird die Kunst der gestalteten Fälle in unserer Lehre über die Verknüpften begründet. Denn die Rechtsgelehrtheit ist in anderen ähnlich der Geometrie, ferner ist was diese als Bestandteile hat, bei der anderen der Fall. Bestandteile sind einfache, in der Geometrie Figuren: Dreieck, Kreis, u. s. w. in der Rechtsgelehrtheit: Verfahren, Zusage, Rechtsübertragung, u. s. w. Die Fälle: die Verknüpfung derer, die nach beiden Seiten unendliche variabel sind. Die Bestandteile der Geometrie hat Euklid zusammengestellt, die Bestandteile des Rechts sind in deren Sammlung enthalten, auf beiden Seiten werden jedoch außerordentlich Fälle zugemischt. Aber die einfachen Begriffe in der Rechtswissenschaft, durch deren Mischung weitere entstehen, und gleichsam die Gemeinplätze, und die höchsten Arten zu sammeln hat Bernardus von Lavinheta begonnen, ein Mönch aus dem Orden der Minoriten, in der Sammlung der Ars Magna des Llull, siehe diesen.
Wir sehen das so: Begriffe deren Verknüpfung in der Rechtspflege entsteht durch die Verschiedenheit der Fälle sind: Personen, Gegenstände, Taten, Recht. Die Arten der Personen sind bald natürliche wie: Mann, Frau, Zwitter, Ungeheuer, Tauber, Stummer, Blinder, Kranker, Neugeborener, Knabe, Jüngling, Bursche, Mann, Greis, so wie auch andere zu wünschende Unterschiede aus dem Körperlichen, die einen besonderen Einfluss auf das Recht hätten; bald künstliche, allerdings Lebensarten, Körperschaften oder Vereine und ähnliches. Berufsbezeichnungen gehören nicht zu dieser, weil sie verknüpft werden aus Fähigkeit und Verpflichtung; aber zum Recht.
Dinge sind bewegliche, unbewegliche, teilbare (einheitliche), unteilbare, körperliche, unkörperliche, und insbesondere: der Mensch, das zahme Tier, das Wildtier, das Raubtier, der Schädling; das Pferd, das Wasser, Grund und Boden, das Meer u. s. w., und insgesamt alle Dinge, zu denen es ein besonderes Recht gibt. Deren zu suchenden Unterschiede stammen von den Physikern.
Die Geschäftsvorgänge (aber nicht die Handlung oder der Zustand) ist zu erwägen wie natürliche: so teilbare, unteilbare es verbleiben vollendete Abschlüsse oder sie sind vorübergehend gemacht; Besitztum das ein materielles Eigentum ist, Übergabe, Diebstahl, Gewalt, Mord, Verletzung; Schuld, hierhin der Umstand der Zeit und des Ortes, diese Unterschiede sind ebenso aus der Physik zu verlangen; zu den moralischen: so sind Taten freiwillige, erzwungene, unumgängliche, vermischte, bedeutende, unbedeutende; unter den bedeutenden Worte, Ratschläge, Aufträge, Anweisungen, Versprechungen, Annahmen, Verabredungen. Diese ganze Vielfalt der Worte und die Bedeutung von den Sprachlehrern. Endlich haben Geschäftsvorgänge entweder eine Wirkung des Rechts oder nicht und jene gehören allerdings zur Liste der Gesetzessammlung die sie erzeugen, diese sind von staatlichen und moralischen reich aufzuzählen.
Der Gegenstand der Rechte werden auf gleiche Weise aufgezählt oder unterschieden nach der Art. Und diese sind freilich z. B. gegenständliche, persönliche; reine, verbreitete, unbestimmte; bewegliche oder einer Person oder einer Sache zugehörige u. s. w. Gattungen z. B. uneingeschränkt Besitzrecht, Nutzungsrecht; Lehndienste mit Sachen oder persönlich; oder Nießbrauch; Eigentumsnutzung, das Recht in Besitz zu nehmen, die Verabredung durch Verjährung zu erwerben; Zwang, Verpflichtung (tätig genommen); Dienstzwang, Leitungszwang, Möglichkeit Zwang auszuüben. Ferner die gemäß dem Gesetz das zu anzuwenden ist angewandten Rechtsgeschäfte sind folgende: Beschwerde, oder das Recht den Wunsch darzulegen vor Gericht, dessen Art gemäß der Begründung der Ordnung: Klage, Verteidigung, Gegendarstellung, u. s. w. nämlich in der Verhandlung; bald in Schriftform oder anderen außerhalb des Termins; das Bittgesuch für die Vorladung durchzusetzen zur Überprüfung, u. s. w. Aber die Sammlung der Gesetze wird nur aus der Rechtswissenschaft vollzogen.
Wir haben hier schnell alles angeführt was in den Sinn kommt, wenigstens dass unser Verstand erkannte; andere einfache Begriffe können durch eigenen Fleiß ergänzt werden. Wir haben hier schnell alles angeführt was in den Sinn kommt, wenigstens dass unser Verstand erkannte; andere einfache Begriffe können durch eigenen Fleiß ergänzt werden. Aber so dass er bloß diese Begriffe verwendet, die umgekehrt wieder einfache sind, das ist deren Vorstellung nicht aus anderen einheitlichen zusammengesetzt wird, obgleich an allgemeinen Stellen, deren Anordnungen gegenwärtig auf einen sehr mächtiger Kunstgriff zurückgeht, wird es möglich sein die umfassten Begriffe durch einfache sehr benachbarte auch gleich wie einen eigentümlichen Titel anzuordnen, z. B. die Entschädigung, die zusammengesetzt wird aus der Verpflichtung des Titius dem Gaius und desselben Gaius dem Titius in der teilbaren Sache , einheitlich oder gleichmäßig, die von beiden in höchster Eintracht gelöst wird. (vgl. G. W. Leibniz: De Casibus Perplexis, XVIII)
Aus der Verknüpfung von 2, oder, 3 u. s. w. deren einfachen Begriffe, bald mit sich selbst mehrfach wiederholt, bald mit anderen und in derselben Zusammenstellung, durch Veränderung der Stellung schreitet die Ordnung des Falls fast grenzenlos fort wer sieht das nicht? Sogar wer dies genauer untersuchen wird, wird Regeln finden zur Ermittlung einzigartigere Fälle u. s. w., wir haben einiger dieser Art zusammengefasst, aber bisher unvollendetere, als dass wir wagen sie anzufügen.
Entsprechend ist die Überlegung der Begriffe in der Theologie, die geradezu irgendwie eine spezielle Rechtswissenschaft ist, aber mit derselben grundsätzlichen Bedeutung der anderen. Denn es ist wie ein gewisses Lehrgebiet des öffentlichen Rechts, das die Menschen im Staat Gottes festhält, wo die Ungläubigen gleichsam Widerspenstige sind, die Kirche wie die guten Untertanen, die geistlichen Personen, sogar auch die öffentlichen Würdenträger wie die untergeordneten Würdenträger, Exkommunikation wie Kirchenbann, die Lehre von der Heiligen Schrift und dem Wort Gottes wie von den Gesetzen und deren Auslegung; vom Kanon welcher die ursprünglichen Gesetze, von den grundsätzlichen Irrtümern gleichsam von den Kapitalverbrechen, vom letzten Gericht des jüngsten Tages wie vom Gerichtsprozess und dem vorherbestimmten Ende, von der Erlass der Sünden wie von Recht zu begradigen, von der ewigen Verdammnis wie von der Todesstrafe u. s. w.
-
So weit zum Gebrauch der Verknüpfungen in den Einteilungen zu findenden; es folgt die neunte Anwendung: Aus den gegebenen Arten der Teilung, die vorläufige Einteilung oder untergeordnete Gattungen und Arten zu finden. Und zwar wenn nämlich die Teilung, deren Arten gegeben sind, die Dichotomie ist, hat die Fragestellung keine Bedeutung, denn diese ist auch nicht weiter kürzbar; wenn aber eine Polytomie ganz und gar.
Denn es ist die Trichotomie unter den Polytomien die kleinste, oder drei Arten der gegebenen Gattung: a, b, c; die Verknüpfung von 3 dieser ist deshalb so viel wie 1 in der obersten gegebenen Gattung; die Vereinigungen aber 3; dort geht die höchste Gattung selbst hervor, hier die unterste Art selbst, zwischen die Verknüpfung von 3 aber und die Vereinigung es verbleibt nur die Verknüpfung von 2. Aber es gibt 3 Verknüpfung von 2 für drei Dinge, daher entstehen 3 dazwischen liegende Gattungen, nämlich abgeleitet oder die folgende nächste Gattung ab, ebenso die folgenden bc, ebenso die folgenden ac. Ab er zu einer Gattung wird benötigt, dass sie bald einzelnen entspricht, bald dass es von allen angenommen entgegengesetzt veränderbar sei.
Durch ein Beispiel wird die Sache deutlicher. Der gegebene Gattungsbegriff sei der Staat, er wird 3 Arten haben, an der Stelle A die Monarchie, als B die Oligarchie, Polyarchie oder die Aristokratie, an Stelle von C die Panarchie; denn zweimal werden wir bequemst von den Begriffen Gebrauch machen, damit es ersichtlich wird, und vom Begriff der Panarchie wenn auch in anderem Sinne, wird von Bruder Patritius im Band seiner eigentümlichen Werke so betitelt, in dem er die himmlischen Rangordnungen erklärt hat. So wie von der Bezeichnung der Polyarchie gewöhnlich für Oligarchie und Panarchie gebraucht wird von Marcus Zuerius van Boxhorn im Buch 2 Kapitel 5 des Werks "Staatliche Ordnungen" also 1) die nachgeordnete Gattung die folgende AB oder der Monarchie und der Adelsherrschaft sei die Oligarchie.
Denn es herrschen entweder nicht alle: Oligarchie oder aber einer: Monarchie, oder viele: Oligarchie, Polyarchie, oder alle: Panarchie. 2) die folgende nachgeordnete Gattung BC wird die Polyarchie sein; denn es regiert entweder einer: Monarchie, oder viele: Polyarchie (in der entweder nicht alle: Polyarchie. Oligarchie, oder alle: Panarchie). 3) die nachgeordnete Gattung folgende AC ist der oberste Staat. Denn die Art des Staates die eine liegt zwischen der Aristokratie (daher auch der doppelte Name: Oligarchie Polyarchie), die andere die höchste. Die äußersten aber sind in denen einer regiert, ebenso in denen alle regieren.
So haben wir in den geringsten offenbar die Polytomie, Trichotomie dem Gebrauch der Verknüpfungen folgend gemacht, wie viele, bitte ich sehr, in der Einteilung der Eigenschaften in 11 Arten, sie werden von anderen ähnlichen Veränderungen sein? Wo nicht nur einzelne Verknüpfungen von 2, sondern auch von 3 u. s. w. bis zu Verknüpfungen von 10, und es werden durch berechnete Gattung in der Höhe und durch schwache Arten in der Welt die Verknüpfungen oder die möglichen Gattungen und Arten 2047 sein.
Denn unser Sinn ist sicherlich so sehr schöpferisch beim Ableiten, dass er aus wie vielen gegebenen Dingen auch immer, die Gattung derer finden kann, das ist die gemeinsame Vorstellung von einzelnen und außer denselben keine. Allerdings wenn er es auch nicht finden würde, wird Gott es wissen, die Engel werden es finden; deshalb ist es die Grundlage aller derartiger Abstraktionen.
Diese ergeben eine so große Mannigfaltigkeit der nachgeordneten Gattungen, dass in vorläufig Eingeteilten oder in zu erstellenden Tabellen, auch beim Finden von irgendjemandem gegebenen in den untersten Arten der Einteilung betreten die Autoren verschiedene Wege die Brauchbarkeit, und sie gelangten alle nichtsdestoweniger bei denselben Unterarten. Das wird erkennen, wer die Scholastiker nach der Anzahl der Kategorien der Kardinaltugenden befragt, der von Aristoteles erkundenden abgezählten Tugenden, Stimmungen u. s. w.
-
Es ist Zeit von den Einteilungen zu den Aussagesätzen zu kommen, ein anderer Teil der logischen Erfindungen. Der Aussagesatz besteht aus dem Subjekt und dem Prädikat, deshalb sind alle Aussagesätze Verbindungen von 2. Deshalb ist die Fragestellung der analytischen Logik der Aussagesätze zu lösen: 1) zu dem gegebenen Subjekt die Prädikate; 2) zu dem Prädikat die Subjekte zu finden, und von beiden bald bestätigend bald verneinend.
 Das hat Ramon Llull im Opusculum Raymundinum de Auditu Kabbalistico, Tractat 1, Kapitel Abbildung 1 Seite 46 erkannt, und wo er die vorigen wiederholt auf Seite 239 der Ars Magna. Dieses, damit er zeige, vie viele neue Vordersätze aus jenen seinen sehr allgemeinen Begriffen: Güte, Größe, Dauer u. s. w. entstehenm, welche einzelnen von einzelnen erklärt werden können sagt er, er zeichnet einen Kreis dem er eine regelmäßige neuneckige Figur einschreibt, an jede Ecke schreibt er einen Begriff, und von jeder Ecke zu jeder anderen zieht er eine gerade Linie. Es gibt 36 solcher Linien, so viele wie Verknüpfungen von 2 für 11 Dinge. Und weil die Stellung in jeder beliebigen Vereinigungen von 2 zweifach verändert werden kann, oder ein beliebiger Vordersatz einfach verwandelt wird, erzeugt er 36 · 2 macht 72, das ist die Anzahl der llullianischen Vordersätze. Allerdings wird der gesamte Kunstgriff Ramon Llulls von solchen Verknüpfungen vollendet, siehe dessen Werke in Strasburg im Jahre 1698 im Oktavformat herausgegeben Seiten 49, 53, 68, 136, die wiederholt werden auf den Seiten 240, 244, 245. Ebenso hat er eine übereinstimmende Tabelle erstellt mit 84 Spalten, deren jede 20 Verknüpfungen enthält, in denen zählt er die Zusammenstellungen von 4 seiner Ordnung mit alphabetischen Buchstaben bezeichnet; diese Tabelle nimmt die Seiten 260 bis 266 ein. Eine Tabelle der Zusammenstellungen von 3 aber findet man bei Heinrich Cornelius, gen. Agrippa von Nettesheim in "Kommentare zu Raymund Llulls kurze Kunst", die 9 Seiten einnimmt, von Seite 863 bis einschließlich 871. Dieselben führt zum größten Teil aus, aber kürzer Johann Heinrich Alsted in "Der Aufbau der Kunst Llulls" enthalten in dessen Sammlung der "Kunst zu erinnern" Seite 47 und folgende.
Das hat Ramon Llull im Opusculum Raymundinum de Auditu Kabbalistico, Tractat 1, Kapitel Abbildung 1 Seite 46 erkannt, und wo er die vorigen wiederholt auf Seite 239 der Ars Magna. Dieses, damit er zeige, vie viele neue Vordersätze aus jenen seinen sehr allgemeinen Begriffen: Güte, Größe, Dauer u. s. w. entstehenm, welche einzelnen von einzelnen erklärt werden können sagt er, er zeichnet einen Kreis dem er eine regelmäßige neuneckige Figur einschreibt, an jede Ecke schreibt er einen Begriff, und von jeder Ecke zu jeder anderen zieht er eine gerade Linie. Es gibt 36 solcher Linien, so viele wie Verknüpfungen von 2 für 11 Dinge. Und weil die Stellung in jeder beliebigen Vereinigungen von 2 zweifach verändert werden kann, oder ein beliebiger Vordersatz einfach verwandelt wird, erzeugt er 36 · 2 macht 72, das ist die Anzahl der llullianischen Vordersätze. Allerdings wird der gesamte Kunstgriff Ramon Llulls von solchen Verknüpfungen vollendet, siehe dessen Werke in Strasburg im Jahre 1698 im Oktavformat herausgegeben Seiten 49, 53, 68, 136, die wiederholt werden auf den Seiten 240, 244, 245. Ebenso hat er eine übereinstimmende Tabelle erstellt mit 84 Spalten, deren jede 20 Verknüpfungen enthält, in denen zählt er die Zusammenstellungen von 4 seiner Ordnung mit alphabetischen Buchstaben bezeichnet; diese Tabelle nimmt die Seiten 260 bis 266 ein. Eine Tabelle der Zusammenstellungen von 3 aber findet man bei Heinrich Cornelius, gen. Agrippa von Nettesheim in "Kommentare zu Raymund Llulls kurze Kunst", die 9 Seiten einnimmt, von Seite 863 bis einschließlich 871. Dieselben führt zum größten Teil aus, aber kürzer Johann Heinrich Alsted in "Der Aufbau der Kunst Llulls" enthalten in dessen Sammlung der "Kunst zu erinnern" Seite 47 und folgende.Es gibt aber diese einfachen Begriffe:
- I. Vollkommene Eigenschaften: Güte, Größe, Dauer, Macht, Weisheit, Wille, Tugend, Wahrheit, Ruhm;
- II. Bezogene: Verschiedenheit, Eintracht, Gegensatz, Grundsatz, Vermittelndes, Ende, Mehrheit, Gleichheit, Minderheit;
- III. Fragen: wer von beiden, was, von wem, warum, wie viel, wie beschaffen, wann, wo, auf welche Weise (mit wodurch);
- IV. Subjekte (Handelnde): Gott, Engel, Himmel, Mensch, Vorstellung, Wahrgenommene, Lebende, Grundlegende, Benutzbare;
- V. Tugenden: Gerechtigkeit, Klugheit, Mut, Mäßigung, Glaube, Hoffnung, Nächstenliebe, Geduld, Barmherzigkeit;
- VI. Sünden: Habgier, Fresssucht, Verschwendung, Hochmut, Verdruss, Missgunst, Zorn, Lüge, Unbeständigkeit.
Wenn auch Janus Cäcilius Frey in "Via ad divas scientias artesque, linguarum notitiam, extemporaneos sermones nova et expedita" Teil XI, Kapitel I die 3. Und 6. Klasse auslässt.
Weil somit in den einzelnen Klassen 9 Dinge sind, und 9 Dinge 511 einfache Verknüpfungen haben, werden in einzelnen Klassen ebenso viele Verknüpfungen sein, ferner ist herzuleiten nach Fragestellung 3 Klasse für Klasse 511 · 511 · 511 · 511 · 511 · 511 macht 17.804.320.388.674.561, die sechste Potenz von 511. Dass ich alle jene Veränderungen beiseitelasse, durch die der gleiche Begriff wiederholt wird, ebenso durch die eine Klasse wiederholt wird, oder aus einer Klasse mehrere Begriffe eingesetzt werden.
Und diese sind nur Verknüpfungen, zu denen ich sagen würde es sind Veränderungen der Stellung, wenn sie in Verknüpfungen gezogen werden würden. Und deshalb werde ich hier nebenbei die Fragestellungen erklären: "Die Veränderungen der Stellung oder die Anordnungen in Verknüpfungen zu ziehen, oder von gewissen gegebenen Dingen alle Veränderungen ebenso der Verknüpfung oder der Materie, wie den Platz oder die Form ist zu finden. Alle einzelnen Verknüpfungen der gegebenen Anzahl werden zusammengezählt (z. B. von der Anzahl 4: 4 Vereinigungen, 6 Zusammenstellungen von 2, 4 Zusammenstellungen von 3, 1 Zusammenstellung von 4) es wäre die Veränderung der Anordnung einzelner Exponenten gefragt nach Fragestellung 4 unten (z. B. 1 gibt 1, 2 gibt 2, 3 gibt 6, 4gibt 24), diese wird multipliziert mit der Verknüpfung ihrem einzelnen oder über den gegebenen Exponenten (z. B. 1 · 4 macht 4, 2 · 6 macht 12, 4 · 6 macht 24, 1 · 24 macht 24). Die Zusammenstellung aller Faktoren wird aus der Zusammenführung der Anordnungen in Verknüfungen gemacht, das ist das gesuchte (z. B. 4 + 12 + 24 + 24 macht 64)". Aber von den Begriffen Ramon Llulls wünsche ich mehr.
Denn dessen Vorgehen ist mehr auf die zu erörternde Kunst aus der Zeit gerichtet, als die vollkommene Wissenschaft von der gegebenen zu erfassenden Sache, wenn nicht aus Absicht Ramon Llulls, sicher aus der seiner Anhänger. Die Anzahl der Begriffe hat er nach Ermessen bestimmt, daher sind es 9 in den einzelnen Klassen. Warum hat er unter die absoluten Prädikate, die völlig abstrakt sein sollen, Wohlwollen, Wahrheit, Weisheit, Mut, Ruhm zusammengenommen, warum hat er Schönheit ausgelassen, oder Figur, warum Anzahl? Den relativen Prädikaten hätte er sehr viel mehr zurechnen müssen, z. B. den Grund, das Ganze, den Teil, das Erforderliche, u. s. w. Darüber hinaus Mehrheit, Gleichheit, Minderheit ist nichts anderes als Übereinstimmung und Unterschied der Größe. Zu den Fragen nach den vollständigen Prädikat-Klassen gehört: wer von beiden es wäre, ist des Daseins, das die Dauer an sich zieht; was des Wesens; warum, des Grundes, von wem, des Objekts; Wie viel, der Größe, wie beschaffen, der Beschaffenheit, die die Gattung der absoluten Prädikate ist; wann, der Zeit; wo, des Ortes; auf welche Weise, der Form; mit wem, des Begleiters: alle Begriffe sind, welche entweder bezogen sind auf Prädikate, oder darauf gerichtet. Und warum er wie lange auslässt, ob es nicht mit der Dauer zusammenfiele? Warum er also andere gleiche Übereinstimmung dazu gibt, schließlich werden auf welche Weise und mit wem unglücklich vermischt.
Die letzten Klassen aber, Sünden und Tugenden sind geradewegs vom Allgemeinwissen so weit unentdeckt. Auch ist die berichtigende Durchsicht selbst derer wie ist sie zum Teil unvollständig, zum Teil überflüssig! Er hat die ersten 4 der Kardinaltugenden betrachtet, dann 3 theologische, warum nun aber Geduld zugefügt wird, die von der Tapferkeit umfasst wird wie man sagt; warum die Frömmigkeit, das ist die Liebe Gottes, die in der Nächstenliebe enthalten ist? offenbar um die Lücke zu den Neun auszufüllen. Warum hat er auch die Sünden selbst nicht als Gegenteil der Tugenden betrachtet? Als ob wir nicht verstünden, dass in der Tugend das Gegenteil, und in der Sünde die Tugend ist? aber in den Sünden werden 27 herausstehen. Denn es gibt hauptsächlich diese Grade des Seins: Gott, Engel, Himmel (nach der peripatetischen Lehre ein unzerstörbares Seiendes), Mensch, vollkommene Bestie (oder eine Vorstellung habend), unvollständige (oder nur einen Sinn, gleich wie sie von den Zoophyten erzählen), Pflanzen. Die gemeinsame Form der Körper (welche aus der Zusammenmischung der Grundstoffe entstehen, die sich auf alle unbelebten beziehen.), Die künstlichen (die er Werkzeuge nennt). Diese sind es deren Verknüpfung Ramon Llull benutzt, über die das Urteil, jedenfalls ausgereift, des ehrwürdigen Mannes Pierre Gassendi in einem besonderen Kapitel der Werke seiner epikureische Logik T. 1. Deshalb hat vor einiger Zeit Giordano Bruno (Nolano) im Vorwort der Durchforschung auf Seite 684. es die Kunst der Verknüpfung von 2 Ramon Llulls genannt.
Aber ich meine, es ist was der unsterbliche Athanasius Kircher jene seine lange versprochene große Kunst des Wissens, oder neue Pforte der Wissenschaften, durch den Titel Verknüpfungen von2 gezeigt hatte, welche über alle Dinge durch grenzenlose Überlegungen erörtert wird, und die Zusammenfassung aller Erkenntnis enthalten kann (auf diese Weise hat Pierre Grégoire aus Toulouse seine Syntax der wunderbaren Kunst beschrieben) unter der Bezeichnung Verknüpfung von 2 gezeigt hat. Deshalb wünsche ich eines, dass ein Mann mit riesigem Verstand erhabener als sowohl Ramon Llull als auch Pierre Grégoire aus Toulouse in das innerste der Dinge eindränge, und was wir zuvor angenommen haben, deren Entwürfe wir hergeleitet haben, welche wir unter unsere Wünsche setzen, vollendete, was über den verhängnisvollen Erfolg dessen bei der Erklärung der Wissenschaften nicht anzuzweifeln ist. Und wir haben uns dies gewiss nicht vorgenommen nicht sowohl der vermehrten Arithmetik, und wenn wir es auch gemacht haben, als der analytischen Logik die Quellen zu öffnen, durch die Aufgabe des Herolds die Fliehenden, und was in der Liste der Wünsche von seinem Zuwachs der Wissenschaften Francis Bacon, Baron Verulam gemacht hat, was für hinreichend zu halten ist, wenn der Argwohn solcher Künste von den Menschen erzeugten, wie er mit unglaublichem Erfolg der menschlichen Art anderes hervorbrächte.
Deshalb betreibe denn der Kombinatorik (denn so wollen wir lieber, denn nicht jede Verknüpfung ist eine Zusammenstellung von 2) dass uns das Festzustellende sichtbar werde, zeichnen wir einen ersten Entwurf. Der gründlichste Untersucher der Grundlagen in allen Dingen Thomas Hobbes hat verdientermaßen alle Werke unseres Verstands als Berechnung gesetzt, aber diese werden erlangt entweder durch die Summe zu addieren oder die Differenz zu subtrahieren; in "Erster Teil der Grundlagen der Philosophie über Körper" Kapitel 1 Absatz 2. Deshalb gibt es auf welche Weise auch immer zwei hauptsächliche Zeichen der Algebraiker und der Analytiker + und -, dergestalt zwei gewissermaßen Verknüpfungen ist und ist nicht: jenes setzt der Verstand zusammen, dieses trennt er. In diesem Sinne ist deshalb dieses "Ist" und "ist nicht" keine passende Verbindung, sondern Teil des Merkmals; es gibt aber zwei Verknüpfungen, eine benannt "nicht", die andere unbenannt, sie wird aber eingeschlossen in "ist", jedes Mal selbst nicht zugefügt: "nicht", was er selbst gemacht hat, dass dieses "Ist" für eine Verbindung gehalten werde. Wir könnten einen Hilfsausdruck anwenden: "in der Tat", z. B. Der Mensch ist in der Tat ein Tier. Der Mensch ist nicht ein Stein. Aber dies nebenbei.
Ferner wenn aus diesen feststeht alles würden zuwege gebracht, um dessen Kunst Kategorien aufzustellen und wie das Thema der Analyse anzuwenden ist. Die Analyse ist dies:
- Jeder gegebene Begriff wird in formale Teile zerlegt, oder dessen Definition würde aufgestellt werden; diese Teile aber wiederum in Teile oder die Definition der Definition der Begriffe; so lange bis zu den einfachen Teilen oder unbestimmten Begriffen. Denn ού δεἰ παντὀς ὃρον ζητεἰν; und die letzten jener Begriffe werden nicht mehr durch die Definition, sondern durch Entsprechung verstanden.
- Alle gefundenen Hauptbegriffe werden in eine Klasse gelegt, und sie würden bezeichnet werden mit gewissen Merkmalen; es wird bequem sein sie zu nummerieren.
- Unter die Hauptbegriffe werden nicht nur Dinge gegeben, sondern auch Verfahren und Betrachtungen.
- Weil alle entstandenen Begriffe den Abstand zu den Hauptbegriffen verändern, je nachdem aus den vielen hauptbegriffen sie zusammengesetzt werden, oder je nach dem was der Exponent der Verknüpfung ist, daher sind so viele Klassen zu machen, wie es Exponenten gibt, und in jede Klasse werden Begriffe zusammengefasst, die aus der selben Zahl erster zusammengesetzt wurden.
- Die entstandenen Begriffe wird man nicht anders als durch Verknüpfung von 2 beschreiben können, wie die zuschreibenden Hauptbegriffe, aus denen sie zusammengesetzt wurden, und weil die Hauptbegriffe durch Zahlen bezeichnet sind, würden zwei Zahlen den zwei Begriffen zugeschrieben werden.
- Aber die durch Verknüpfung von 3 entstandenen Begriffe oder auch die Verknüpfungen anderer größerer Exponenten, oder Begriffe die in der 3. und folgenden Klasse sind, einzelne können ebenso oft unterschiedlich geschrieben werden, wie viele hat ein Exponent Verknüpfungen einfach betrachtet nicht mehr wie der Exponent, aber wir die Anzahl der Dinge. Der Gebrauch IX hat hier seine Grundlage, z. B. sollen die ersten Begriffe mit diesen Zahlen bezeichnet 3, 6, 7, 9, und es wäre der entstandene Begriff in der dritten Klasse, oder die durch Verknüpfung von 3 gebildeten, nämlich aus 3 einfachen 3, 6, 9, und es seien in der zweiten Klasse die Verknüpfungen diese: [1] 3 6 [2] 3 7 [3] 3 9 [4] 6 7 [5] 6 9 [6] 7 9. Ich behaupte jene gegebenen Begriffe der dritten Klasse können entweder so geschrieben werden: 3 6 9, alle sind einfache auszudrücken; oder einen einfachen auszudrücken, und an Stelle der beiden übrigen einfachen eine Verknüpfung von 2 zu schreiben, z. B. so: ½ 9 oder 3⁄2 6 oder 5⁄2 3. Was diese gleichsam Brüche bedeuten wird gleich gesagt werden. Aber um wieviel die Klasse von der ersten entfernter ist, desto größer ist die Veränderung. Denn immer sind die Begriffe der vorhergehenden Klasse gewissermaßen untergeordnete Arten zu den gewissen Begriffen der nachfolgenden Veränderung.
- Jedes Mal wenn der entstandene Begriff außerhalb seiner Klasse erwähnt wird, wird er nach Art des Bruchs geschrieben, dass die obere Zahl oder der Zähler die Nummer der Stelle in der Klasse ist; die untere oder Nenner, die Nummer der Klasse.
- Es ist bequemer, in den darzustellenden gebildeten Begriffen nicht alle Hauptbegriffe, sondern die dazwischen liegenden zu schreiben, wegen der Vielzahl, und aus diesen jene sich zeigen die am meisten von der Sache verstehen. Aber alle Hauptbegriffe zu schreiben ist grundlegender.
- 9) Diese können so aufgestellt werden, dass alle Subjekte und Prädikate gefunden werden, sowohl die bekräftigenden wie die negierenden, sowohl die allgemeinen wie die eingeschränkten. Denn die Prädikate der gegebenen Subjekte sind alle Hauptbegriffe dessen; ebenfalls alle ähnlichen gebildeten von den Hauptbegriffen, deren sind alle Hauptbegriffe in den gegebenen gegeben. Wenn also der gegebene Begriff, der ein Subjekt sein muss, als Hauptbegriff geschrieben worden ist, ist es leicht diejenigen ersten zu finden, die von selbst vorhergesagt würden, die gebildeten aber auch zu finden wird gegeben, wenn in den anzuordnenden Verknüpfungen die Reihenfolge bewahrt worden ist. Wenn der gegebene Begriff zu den gebildeten geschrieben worden ist, oder zum Teil zu den gebildeten, zum Teil zu den einfachen, jeder der hervorgehoben werden wird von dessen gebildeten, wird von den gegebenen hervorgehoben werden. Und diese sind freilich alle Prädikate der weiteren von den engeren, die Bekanntmachung aber ist gleich von den gleichen, weil die Definition von dem Begriff, das ist entweder sind alle der Hauptbegriffe dessen oder gebildete, oder die gebildeten und einfachen, in denen alle jene Hauptbegriffe enthalten sind, werden festgelegt von dem gegebenen. Diese sind so viele, wie von den Verfahren die wir gerade gesagt haben, es kann ein Begriff geschrieben werden.
Aus diesen wird nun einfach sein, durch die Zahlen alle Prädikate zu erforschen, die von jedem gegebenen Subjekt erklärt werden können, oder alle U A. Die Aussagen von dem gegebenen Subjekt, allerdings von der ersten der einzelnen Klassen bis einschließlich zu der gegebenen Klasse, werden die Zahlen selbst in der Reihenfolge ihrer Nenner oder Exponenten gesetzt, z. B. 1. (für die erste Klasse), 2. (für die zweite Klasse), 3. 4. u. s. w. Jedem einzelnen würde so wie nicht mehr länger dem Exponenten, sondern wird ihre einfache Verbindung mit der Zahl zugewiesen z. B. 1 3 7 15, 6 Verbindungen von 2, 4 Verbindungen von 3, 1 Verbindung von 4; die einzelnen einfachen Verknüpfungen der Klassen werden multipliziert mit der besonderen Verknüpfung der höchsten Klasse, die den gleichen Exponenten mit der Zahl ihrer Klasse hat, z. B. 1 · 4 macht 4, 3 · 6 macht 18, 4 · 7 macht 28, 15 · 1 macht 15; die Addition aller Faktoren wird die Anzahl aller Prädikate des gegebenen Subjekts sein, so dass es für die Aussage UA ist, z. B. 4 + 18 + 28 + 15 macht 65.
Die Prädikate für die Aussagesätze PA oder die Anzahl der besonderen verstärkenden Aussagesätze werden so untersucht: die Prädikate UA des gegebenen Begriffs werden gefunden, wie vor kurzem gesagt worden ist, und die Subjekte UA, wie in Kürze erklärt werden wird; beide Zahlen werden addiert, weil aus dem Aussagesatz UA PA entsteht, entweder durch einfache Umkehrung, oder durch Unterordnung; das Ergebnis wird das gesuchte sein.
Die Subjekte im Aussagesatz UA des gegebenen Begriffs sind entweder alle gebildeten Begriffe, in denen der gegebene Begriff enthalten ist, welche nur in aufeinander folgenden Klassen vorkommen, und daher entsteht ein engeres Subjekt, oder alle gebildete Begriffe die die gleichen einfachen Begriffe mit dem gegebenen enthalten, mit einem Wort die Definitionen desselben Begriffs, oder die Veränderungen diesen zu schreiben, dass sie gegenseitig gleiche Subjekte sind.
Die Anzahl der Subjekte werden wir so berechnen: man finde die Anzahl aller Klassen. Von diesen gibt es so viele, wie erste Begriffe in der ersten Klasse sind, z. B. gibt es in der ersten Klasse so viel wie 5 Begriffe, wird es auf der Welt 5 Klassen geben, nämlich in der ersten Vereinigungen, in der zweiten Verknüpfungen von 2, in der dritten Verknüpfungen von 3, in der vierten Verknüpfungen von 4, in der fünften Verknüpfungen von 5. So wird auch die Anzahl aller folgenden Klassen gefunden werden, durch Subtraktion der Zahl der Klasse der gegebenen Begriffe, z. B. 2 von der Anzahl der universellen Klassen 5, es verbleibt 3. Die Anzahl der Klassen aber oder der Hauptbegriffe unterstellen wir als Anzahl der Dinge, die Anzahl der Klasse dem Exponenten, es wird die Anzahl der Begriffe in der Klasse dasselbe sein mit den besonderen Verknüpfungen durch die Anzahl und den Exponenten, z. B. von 5 Dingen gibt es 5 Vereinigungen, 10 Verknüpfungen von 2 und 3, 5 Verknüpfungen von 4, 1 Verknüpfung von 5; deshalb werden so viele in einzelnen Klassen sein dem Exponenten entsprechend den Begriffen, vorausgesetzt dass es 5 erste Begriffe gibt. Außerdem wird der gegebene Begriff, dessen Subjekt gesucht wird, dem Hauptsatz wird der Verknüpfungen entsprechen; die engeren Subjekte durch die Verknüpfungen selbst ist nämlich der gegebene Hauptsatz. Deswegen werden wir die engeren Subjekte der gegebenen Begriffe finden, wenn wir diese Fragestellung lösen können:
"Bei gegebenem Vordersatz die Verknüpfungen zu finden, ist teils einfach (so werden wir alle engeren Subjekte finden) teils besonders, oder bei gegebenem Exponenten (so werden wir jene finden die in der gegebenen Klasse sind). Die Fragestellung werden wir hier sofort vorläufig lösen, wenn dessen Gebrauch offenbar ist, dass wir wo nicht ohne gesetzt hätten, durch neue Beispiele nötig hätten. Die Lösung ist daher diese: von der Anzahl der Dinge, z. B. 5: a, b, c, d, e wird der Exponent des gegebenen Vordersatzes abgezogen, z. B. a, b 2 - 5 macht 3 oder a 1 - 5 macht 4. Wir nehmen an, dass der gegebene Vordersatz entweder eine Vereinigung ist, oder eine Verknüpfung von 2; denn die Schlussfolgerung verlangt dass es so ist. Der Untersatz wird ebenso vom Exponenten abgezogen, von dem auf gleiche Weise der Exponent des gegebenen Vordersatzes. Wenn deshalb welcher Exponent auch immer gegeben wäre, in dessen Schlussfolgerungen jedes Mal der gegebene Vordersatz wiedergefunden werden würde wäre die Behauptung zu finden, es würde die Schlussfolgerung des so viel kleiner gegebenen Exponenten gesucht werden, wie viel ist der Exponent des gegebenen Vordersatzes, in der Anzahl der Dinge, die wäre auf gleiche Weise so viel kleiner als die gegebene, wie viel der Exponent des gegebenen Vordersatzes ist nach Tabelle א in der Fragestellung 1, das gefundene wird das sein was gesucht wurde. Aber wenn die Verknüpfungen des gegebenen Vordersatzes einfach in allen Verknüpfungen der gegebenen Zahl jeden beliebigen Exponenten, sei die Schlussfolgerung zu finden, die Verknüpfung der Anzahl der Dinge, durch die gegebene so große Anzahl des Untersatzes, so viel ist der Exponent des gegebenen Vordersatzes, es wird das gesuchte sein."
Z. B. wird bei 5 Dingen a, b, c, d, e durch Vereinigung der gegebene Vordersatz a gefunden 1 durch Wechsel (der ist Nichts oder Nichts von 4); der gegebene Vordersatz a b durch Wechsel keine (welche ist über keine Auswahl von 3, wenn ich so sagen soll,); in Verknüpfungen von 2 derer wird durch 4 Wechsel gefunden (welche die Verknüpfungen von 4 sind) diese 1 (welche keine Auswahl von 3 ist), in Verknüpfungen von 3 sind diese 6 (Verknüpfungen von 4) diese 3, (Vereinigung von 3), in Verknüpfungen von 4 jenes 4 (Verknüpfung von 3 von 4) dieses 3 (Verknüpfung von 3), in Verknüpfungen von 5 nach beiden Richtungen 1 im Wechsel (dort Verknüpfung von 4, hier Verknüpfungen von 3 von 3). Diese Verknüpfungen sind bei gegebenem Exponenten, und durch Zusammenfassung deren einfache Verknüpfungen entstehen sie, aber auch so: in den einfachen Verknüpfungen von 5 Dingen (derer 3 sind) wird durch 15 Wechsel gefunden (einfache Verknüpfung von 4), durch 7 Wechsel (einfache Verknüpfung von 3). Diese Verknüpfungen sind die Anzahl der engeren Subjekte des gegebenen Begriffs.
Gleiche Subjekte, jedes mal wenn die Definitionen mit Definitionen unterlegt werden, werden sie nach dem gleichen Verfahren gefunden, wie oben die gleichen Prädikate. Denn die gleichen Begriffe werden veränderlich bewahrt durch Umfang und Beschaffenheit, deshalb werden aus Prädikaten Subjekte gemacht und umgekehrt, die Prädikate aber sind so viele, wie gegebene Begriffe (deren Subjekte gesucht werden) die ersten Begriffe haben einfache Verknüpfungen, z. B. a + 1 + ab + 2. Durch zu den engeren zugefügten gleichen Subjekten 1 + 15 macht 16, 2 + 7 macht 9, erzeugt die Anzahl aller Subjekte des gegebenen Begriffs, welchen zu finden das Ziel war. Die so weit universellen Subjekte, die eingeschränkten bleiben übrig, diese sind so viele wie die eingeschränkten Prädikate.
Die verneinenden Prädikate und Subjekte werden so gefunden: sie werden berechnet aus gewissen gegebenen Hauptbegriffen wie durch die Anzahl der Dinge aller Begriffe sowohl Haupt- wie gebildete Begriffe, so wie die einfachen Verknüpfungen, z. B. wenn die Hauptbegriffe 5 wären, werden es 31 sein; vom Produkt werden alle universellen bejahenden Prädikate und die engeren universellen bejahenden Subjekte abgezogen; der Rest werden alle verneinenden Prädikate sein. Von den Subjekten umgekehrt. Die verneinenden besonderen werden aus den universellen berechnet, wie oben PA aus UA. Wir haben aber die identischen Vordersätze UA übergangen, derer sind so viele wie einfache Verknüpfungen der Hauptbegriffe, oder wie insgesamt die sowohl Haupt- wie gebildeten Begriffe, weil ein beliebiger Begriff entweder ein Haupt- oder ein von sich gebildeter Begriff genannt wird. Außerdem haben wir aus den Verknüpfungen jene ausgelassen, in denen der gleiche Begriff wiederholt wird, welche Wiederholung in einigen die Veränderung im Unendlichen erzeugt, wie bei Zahlen und geometrischen Figuren.
Ferner ist das Verfahren die Argumente zu finden dieses: Es soll jeder gegebene Begriff wie das Subjekt A sein und ein anderer wie beschaffen auch immer wie das Prädikat B sein, gefragt ist der Mittelbegriff: Der Mittelbegriff wird ein Prädikat des Subjekts sein und ein Subjekt des Prädikats, das heißt, der wie auch immer beschaffene Begriff enthält A und ist in B enthalten. Aber man sagt ein Begriff ist in einem Begriff enthalten, wenn alle dessen Hauptbegriffe in jenem sind. Grundlegend aber ist die Darlegung, wenn jeder der beiden Begriffe in erste aufgelöst wird, wird offensichtlich der eine des anderen entweder ein Teil ist oder derselben Teile. Die Anzahl der Mittelbegriffe aber werden wir so finden: Subjekt und Prädikat sind entweder in derselben Klasse, oder in verschiedenen. Wenn in dergleichen, müssen beide Begriffe gebildet sein, und die Veränderung wenigstens der Beschreibung oder der Definition desselben Begriffs, sie werden deshalb zwei Definitionen desselben Begriffs sein können die nur durch einen dritten von einander unterschieden werden. Demnach wird von Anzahl der Definitionen des gebildeten Begriffs, den wir oben im Absatz 69 untersucht haben wird 2 abgezogen, der Rest wird die Anzahl der möglichen Mittelbegriffe zwischen zwei gleichen Begriffen sein.
Wenn sie dagegen nicht in derselben Klasse sind, wird das Prädikat in der Klasse des kleineren Exponenten, das Subjekt in der größeren Klasse sein. Würde nun das Prädikat untergeordnet werden wie der Vordersatz der Verknüpfung, der Exponent der Klasse des Subjekts würde für die Anzahl der Dinge unterstellt. Alle besonderen Schlussfolgerungen des gegebenen Vordersatzes werden aus einzelnen Klassen von der Klasse des Prädikates zur Klasse des Subjekts eingeschlossen gefunden; in einzelnen Klassen werden die Schlussfolgerungen des gegebenen besonderen Vordersatzes in einfache Schlussfolgerungen des Exponenten seiner Klasse multipliziert mit der Anzahl der zugrunde gelegten Dinge. Alle Faktoren zusammengezählt, vermindert um 2 wird das gesuchte sein.
Das Prädikat aber vom Subjekt zu verneinen finden wir einfach: wenn beide vom aufgelösten Begriff in den ersten ist offenbar, dass keines von beiden vom anderen enthalten wird. Denn die negativen können so geprüft werden: alle Prädikate des Subjekts werden gefunden, mit dem von allen verneinte Prädikat, ebenso viele zu prüfende Mittelbegriffe sind verneinend. Alle Subjekte des Prädikats werden gefunden, weil alle vom Subjekt verneint werden, sind auch ebenso viele zu prüfende Mittelbegriffe verneinend. Deshalb werden wir aus beiden berechneten Anzahlen der zu untersuchenden die negativen haben.Endlich ist diese anzuwendende, dass die ganze verwirrende Kunst gerichtet ist auf die Lehrsätze, oder die Vordersätze, die in ewig wahr sind, oder nicht dem Ermessen Gottes, sondern auf ihrer Natur beruhen. Aber alle einzelnen Vordersätze sind gewissermaßen historisch, z. B. Augustus sei der Herrscher der Römer gewesen, oder Beobachtungen, das sind allgemeine Vordersätze, aber deren Wahrheit ist nicht im Wesen, sondern im Sein begründet, jede einzelne ist gewissermaßen zufällig wahr, das ist durch die Willkür Gottes, zum Beispiel alle erwachsenen Menschen in Europa haben die Erkenntnis Gottes. Für solche wird kein Beweis gegeben, sondern eine Annahme, wo nicht was manchmal die Wahrnehmung durch Beobachtung durch Beteiligung eines Lehrsatzes bewiesen werden kann.
Endlich ist diese anzuwendende, dass die ganze verwirrende Kunst gerichtet ist auf die Lehrsätze, oder die Vordersätze, die in ewig wahr sind, oder nicht dem Ermessen Gottes, sondern auf ihrer Natur beruhen. Aber alle einzelnen Vordersätze sind gewissermaßen historisch, z. B. Augustus sei der Herrscher der Römer gewesen, oder Beobachtungen, das sind allgemeine Vordersätze, aber deren Wahrheit ist nicht im Wesen, sondern im Sein begründet, jede einzelne ist gewissermaßen zufällig wahr, das ist durch die Willkür Gottes, zum Beispiel alle erwachsenen Menschen in Europa haben die Erkenntnis Gottes. Für solche wird kein Beweis gegeben, sondern eine Annahme, wo nicht was manchmal die Wahrnehmung durch Beobachtung durch Beteiligung eines Lehrsatzes bewiesen werden kann.
Zu solchen Beobachtungen gehören alle besonderen Vordersätze, die nicht verändert sind oder einem allgemeinen untergeordnet sind. Hier ist deshalb offensichtlich, in welchem Sinne gesagt würde ein einzelner ist kein Beweis, und warum der äußerst gründliche Aristoteles die Ränge der Beweismittel in den Topica gesetzt hätte, wo auch die Vordersätze zufällig sind und die Beweismittel wahrscheinlich. Aber nur die Definition der Beweise ist einzig am Platze. Aber weil es über die zu zeigende Sache jene sind die nicht aus deren Mutterleib ausgesucht werden, z. B. Christus ist in Bethlehem geboren, niemand wird sich durch diese Definitionen wenden, aber die historische Materie wird ausreichen als Erinnerungsort. Nun ist das der Ursprung der Ränge der Topiken, und in einzelnen der größten, durch die alle die Quellen seien, wir hätten wiederholt gezeigt, wenn wir nicht gefürchtet hätten, dass wir nicht im Fortgang der Rede von aller Leidenschaft darzulegen weggerissen würden.
Wenigsten mit einem Wort werden wir anzeigen, dass alles aus der Lehre der Metaphysik zur Beziehung des Seins zum Sein zu wiederholen ist, so dass zwar aus den Beschaffenheiten der Beziehungen der Absätze, aus den Lehrsätzen aber einzelner das meiste gebildet würde. Ich meine dieses gesehen zu haben, gegen den Brauch der Lexikographen des sehr wahrhaften Johann Heinrich Bisterfeld in Phosphorus catholicus seu Artis meditandi epitome herausgegeben in Leiden im Jahre 1657, welches durch Eindringen und Umschreiben begründet ist, wie er sagt, allgemein ist alles in allem, durch Ähnlichkeit ebenso wie auch durch Unähnlichkeit aller mit allen, deren Grundlagen: ist die Beziehung.
Wer dieses Büchlein gelesen hätte, verstünde den Gebrauch der Kunst der Verknüpfung mehr und mehr. Jener scharfsinnige Mann, den wir oft genannt haben, Johannes Hospinianus, hat ein Buch versprochen über das Auffinden und die Bewertung von Möglichkeiten, in dem er die Verbesserung der Topik vorbereitet hatte, und er hatte die 180 Absätze geprüft, die höchsten 2,796, siehe Dialektische Streitfrage Seite 442. Diesen erachte ich zum Schaden für die Zierde der Angelegenheit der Logik niemals herausgegeben. Daher werden wir übergehen, weil wir eine erste Kostprobe einer gewissen Anwendung der Kunst der Verknüpfung von 2 gegeben haben.
Die Mathematik wurde spontan dem Streben angemessen angesehen: daher haben wir nicht von den Hauptbegriffen einfach begonnen, sondern von den ersten zur Mathematik; auch haben wir nicht alle aufgestellt, sondern welche wir zum Hervorbringen der vorgeschlagenen abgeleiteten Begriffe durch ihre Verknüpfung als hinreichend betrachten. Wir hätten gekonnt nach demselben Verfahren alle Definitionen aus den Elementen des Euklid von Alexandria darzustellen, wenn die Zeit ausgereicht hätte. Weil wir ja nicht einfach mit Hauptbegriffen begonnen haben, daher war es nötig die Zeichen zu behandeln, welche Fälle der Wörter und andere die Sprache zu ergänzenden notwendigen verstanden werden. Denn wenn wir nämlich einfach mit Hauptbegriffen beginnen, für die Fälle von Veränderungen selbst, deren Ursprung Julius Caesar Scaliger aus den Beziehungen und der Metaphysik dargelegt hat im Buch über die Fälle der lateinischen Sprachen, würden wir die Begriffe gesetzt haben. Wir haben aber die griechischen Abschnitte hinzugezogen. Mehrere Zahlen haben wir bezeichnet durch zugeschriebene (), 15 falls zwar unbestimmt; 2, 3, u.s.w. wenn bestimmt.
Deshalb soll die Klasse I sein, in der die Hauptbegriffe sind: 1. Punkt, 2. Raum, 3. Zwischenraum, 4. Daneben oder berührend, 5. Auseinander gelegen oder entfernt, 6. Ende oder welche entfernt sind, 7. angestammt, 8. Eingeschlossen (z. B. der Mittelpunkt ist dem Kreis eingeschlossen, dem Umfang eingeschlossen), 9. Teil, 10. Das Ganze, 11. Dasselbe, 12. Unterschiedliches, 13. Eines, 14. Zahl, 15. Mehrere, z. B. 1, 2, 3, 4, 5 u. s. w., 16. Entfernung, 17. Mögliches, 18. Alles, 19. Gegebenes, 20. Bewirktes, 21. Gegend, 22. Ausdehnung, 23. Länge, 24. Breite, 25. Tief, 26. Gemeinsam, 27. Folge oder fortgesetzt Die Klasse II. 1. Die Menge ist 14 von 9 (15), 2. einschließend 6. 10. III. 1. Der Zwischenraum ist 2. 3. 10. 2. Gleiches A folgt 11. ½. 3. Das Zusammenhängende ist A bis B, wenn jedes A zweifellos 9 ist 4 und 7 dann B. IV. 1. Grösser ist A das hat in 9 2⁄3 dann B. 2. Weniger B 2⁄3 dort 9 sein A. 3. Die Linie 2&frasl3; 1 (2). 4. Die Parallele 2&frasl3; in dort 16. 5. Die Zeichnung 24. 8., von 18. 21. V. 1. steigend, was 20. 3⁄4. 2. Fallend, 20. 2⁄4. 3. Verwickelt ist 2⁄3 in dort 11. 22. 4. Schneidend, 3⁄2 in dort 12. 22. VI. 1. Zusammenlaufend, 2⁄5 in dort 16. 2. Auseinanderlaufend. 1⁄5 in dort 16. VII. 1. Oberfläche, 1⁄3 folgend 2⁄4. 2. Unendliches, 1⁄4 wie 18. 19. 17. 3. Rand 3⁄4 13 2⁄2. 4. A. genannt Messung oder er misst B wenn 10 aus A (15) 2⁄3 ist 2⁄2 dann B. VIII. 1. Maximum ist 1⁄4 nicht 2⁄4. 2. Minimum 2⁄4 nicht 1⁄4. 3. Gerade 3⁄4 2⁄3 dort 16. Folgend 6 (2). 4. Welche nicht solches, Kurve. 5. Bogen, 9. Folgt 3⁄7. IX, 1. Rand ist 1⁄7. 2⁄2. X. 1. Gleichmäßige sind, deren 4⁄7. 26. Ist sowohl 1 als auch 2. XI. 2. Winkel ist welche ihn bilden 3⁄3 (2). 4. 2⁄6. XII. 1. Fläche ist 1⁄7. 2⁄3. Hier 16. Folgend 6. XIII. 1. Buckel 1⁄7. 1⁄4 hier 16. Folgend 6. XIV. 1. Geradlinig ist 5⁄4 dessen 2⁄2 ist folgend 3⁄8 (15). 2. Welche Seiten genannt werden. 3. Wenn 3⁄8 (3) Dreieck, 4. Wenn 3⁄8 (4) Viereck u. s. w. XV. 1. Die Mondsichel ist 1⁄3 folgt 5⁄8 (2), nicht 2⁄3 4 (2) [ich merke aber so sehr wie die bucklige Mondsichel, welche der Bogen dem Bogen die Konkavität zuwendet, wie sichelartig welche innen eine andere Konkavität als seine Konvexität.] XVI. 1. Der rechte Winkel ist 1⁄12. 2⁄3. In dann 18. 21. 2. Das Segment ist 3 folgt 2⁄2 und 3⁄8 7. Hier 5⁄4. XVII. 1. Das gleichseitige ist 5⁄4 welches 2⁄2 ist folgend 3⁄8 (15). 3. Das ungleichseitige ist 5⁄4 welches 2⁄2 ist folgend 2⁄8 (3) nicht 2⁄3 (3). XVIII. 1. Der Berührungswinkel ist welchen, sie machen 3⁄4 (2). 4. 2⁄6. Nicht 4⁄5. 27. Doch nur 17. XIX. 1. Eingeschrieben ist 5⁄4 7. welches 1⁄12 (15) sind 4 deshalb 2⁄2. 2. Umschrieben aber ist diese Figur dem sie eingeschrieben ist. XX. 1. Der stumpfe Winkel ist 1⁄4 wie 1⁄16. 2. Der spitze 2⁄4 wie 1⁄16. XXI. 1. Der Durchmesser ist 3⁄8, 1⁄8. 7. hier 5⁄4. XXII. 1. Der Kreis ist 1⁄12. 8. 21. habend in 16. 2⁄3 von 19. Mancher 1 (was 2 genannt wird Kreismittelpunkt) von 18. 6. 2. Das rechtwinklige Dreieck ist 5⁄4 welches 1⁄12 (3) sie sind alle aber 13. Ist 2⁄3 in dann 18. 21. XXIII. 1. Der Mittelpunkt der Figur ist 1. 26. folgt 1⁄21 (15). XXIV. 1. Die gegebene Halbfigur, z. B. der Halbkreis u. s. w. ist 3 folgt 1⁄ 22 und (die Hälfte folgt) 2⁄2. Daher wird es einfach sein die Definitionen zustande zu bringen, wenn beachtet würde, was ich im Absatz 70 in diesen Zeichen gesagt habe, welche durch Brüche beschrieben sind: der Nenner bezeichnet die die Nummer der Klasse, der Zähler die Nummer des Begriffs in der Klasse, z. B. der Mittelpunkt ist 1 (Punkt) 26 (gewöhnliches: folgt 1⁄21 (des Durchmessers) 15 von mehreren. Der Durchmesser ist 3⁄8 (gerade) 1⁄5 (größter) 7 (eingefügt) dort 5⁄4 (der Figur).
Aus diesen, was wir über die Kunst die Wissenschaften zu verknüpfen, oder die analytische Logik erörtert haben, deren Kategorien gewissermaßen durch eine Tabelle derartiger Begriffe dargestellt werden, entsteht gleichsam der Folgesatz oder der Gebrauch XI: eine Universalschrift, das ist von jedem Leser, für jedem einer beliebigen Sprache kundigen verständlich, wie heute mehrere gebildete Männer es versucht haben, deren der sehr gründliche Caspar Schott diese im 7. Buch der " Technica curiosa, sive mirabilia artis" betrachtet, zuerst irgendeinen Spanier, dessen sich Kenelm Digby in " Demonstratio Immortalitatis Animae Rationalis Sive Tractatus Duo Philosophici, In quorum Priori Natura Et Operationes Corporum, In Posteriori vero, Natura Animae Rationalis, Ad evincendam illius immortalitatem, explicantur" Kapitel 28 Nummer 8, und der im Jahre 1653 in Rom gewesen sei, dessen Verfahren diese aus der Natur der Dinge selbst hinreichend scharfsinnig angestrebt: er teilte die Dinge in verschiedene Klassen, in jeder beliebigen Klasse waren eine bestimmte Anzahl der Dinge. So beschrieb er es durch nichts als Zahlen, durch Erwähnung der Nummer der Klasse und der Dinge in der Klasse, doch mit angewandten gewissen Merkmalen der grammatikalischen und orthographischen Beugung. Dasselbe hätte er durch die von uns grundlegender vorgegebenen Klassen gemacht, weil in denen die Anordnung bahnbrechender ist. Ferner Athanasius Kircher, der länger sein neues und umfassendes Druckwerk versprochen hat, schließlich verlangt Johann Joachim Becher, Leibarzt in Mainz, durch ein kleines zuerst in lateinischer Sprache in Frankfurt verlegtes kleines Buch, anschließend auf deutsch im Jahre 1661, dass ein lateinisches Lexikon erstellt werde, wie eine Grundlage, und sie in diesem in gewöhnlicher Sprache rein alphabetisch angeordneten und nummerierten; es würden dann Lexika entstehen, wo die Worte in einer einzigen Sprache nicht alphabetisch angeordnet sind, aber durch die Reihenfolge des Lateins angeordnet sich selbst entsprechend. Sie würden deswegen mit Zahlen geschrieben werden, welche von allen verstanden werden müssen, und wer lesen will, der würde im Lexikon seiner einheimischen Sprache die bezeichnete gegebene Nummer enthüllen, und so wird er es deuten. So wird der Leser hinreichend die Muttersprache verstehen und dieses Lexikon entwickeln, der Schreiber muss (wenn er nicht schon ein alphabetisches Lexikon in seiner Sprache hätte, das auf die Zahlen verweist) und die Muttersprache und Latein zu erfassen, und beide Lexika entwickeln. Aber das Kunstwerk sowohl des Spaniers als auch Johann Joachim Bechers ist sowohl gefällig als auch undurchführbar wegen der Synonyme, wegen der Zweideutigkeit, wegen des sich entwickelnden fortwährenden Verdrusses (weil Niemand die Zahlen jemals dem Gedächtnis übergeben wird), wegen der Heterogenität der Phrasen in den Sprachen.
Aber aus den aufgestellten Tabellen oder aus den Kategorien unserer Kunst der Verknüpfung entstehen größere. Denn die Hauptbegriffe, aus deren Verknüpfung alle anderen aufgestellt werden, würden mit Merkmahlen gekennzeichnet werden, diese Kennzeichen werden gleichsam das Alphabet sein. Es wird zweckmäßig sein die Merkmale wie höchst natürliche zu machen, z. B. für einen Punkt, für die Anzahl Punkte, für die Beziehungen des Seienden zum Sein die Linien, für die Veränderung der Winkel oder die Art der Enden in den Linien der Beziehungen. Wenn diese richtig und scharfsinnig aufgestellt worden sind, wird diese Universalschrift gleichermaßen einfach wie allgemein sein, und was ohne jedes Lexikon gelesen werden kann, und gleichzeitig wird die Erkenntnis der Grundlage aller Dinge aufgenommen. Deshalb wird jede solche Schrift gewissermaßen durch geometrische Figuren sein, und gleich wie durch Bilder, wie einst die Ägypter, heute die Chinesen, aber deren Bilder werden nicht auf ein gewisses Alphabet zurückgeführt oder Buchstaben, durch die gemacht wird dass es einer unglaubliche Belastungs Gedächtnises bedarf, was hier das Gegenteil ist.
-
Nun aber ist hier der 11. Gebrauch der Verknüpfungen nämlich zum Aufstellen einer universellen Schrift. An 12. Stelle werden wir teils gewisse erfreuliche Überlegungen anstellen, teils Verfahren entnommen aus Daniel Schwenters " Deliciae physico-mathematicae oder mathematische und philosophische Erquickstunden" und den Ergänzungen Georg Philipp Harsdörffers, welches Buch die öffentliche Anteilnahme fortsetzt. Im Teil 1 Abschnitt 1 Aufgabe 32 wird die Anzahl der einfachen Verknüpfungen gefunden, die 23 Dinge bilden, z. B. die Buchstaben des Alphabets, nämlich 8.388.607. Im Teil 1 Abschnitt 1 Aufgabe 32 wird die Anzahl der einfachen Verknüpfungen gefunden, die 23 Dinge bilden, z. B. die Buchstaben des Alphabets, nämlich 8.388.607. Im Teil 2 Abschnitt 4 Aufgabe 7 lehrt er die Melodien zu einem gegebenen Text zu finden, von denen uns Georg Philipp Harsdörfferunter in der Aufgabe 6 im selben Teil Abschnitt 10 Aufgabe 25 die geistreiche Entdeckung des Dr. Alexandre de Cossé-Brissac berichtet, durch welche nichts der Verknüpfungeskunst der Wissenschaften passenderes entdeckt werden kann.
Diese, was bei der Kriegsangelegenheit zu beachten ist, dem Herrscher gebührt, so ist es die Verknüpfung: er macht neun Klassen, in der ersten Fragen und Umstände, in der zweiten Zustände, in der dritten Personen, in der vierten Taten, in der fünften Grenzen, in der sechsten Werkzeuge der freien Wirkung, oder von welchen in unserer Möglichkeit Gebrauch zu machen ist, aber diese zu machen, ist nicht; neunten endgültige Taten oder nächste zur Vollstreckung, z. B.
1. Ob. Mit wem. Wo. Wann. Wie. Wie viele. 2. Krieg. Frieden. Waffenruhe. Unterredung. Vertrag. Vermittlung. 3. Landsmänner. Untertanen. Verbündete. Mandanten. Neutrale. Feinde. 4. bleiben. gehen. kämpfen. aufbrechen. Unternehmung. Winterlager. 5. Ruhm. Reichtum. Gehorsam. Würde. Notwendigkeit. Nutzen. 6. Sonne. Wasser. Wind. Wege. Mangel. Gelegenheit. 7. Fahrt. Leitern. Brücken. Hacken. Schaufeln. Schiffe. 8. Geld. Zufuhr. Schmerzpulver. Schmerztablette. Pferde. Heilmittel. 9. Wachposten. Ordnung. Eindruck. Sicherheit. Angriff. Beratungen. Neun Scheiben aus Papier würden hergestellt werden, alle konzentrische und einander umgebend, so dass eine beliebige um die übrigen unbeweglichen gedreht werden kann. So dass die wohin auch immer leicht zu einer neuen Frage verschobene Scheibe, zu einer neuen Verknüpfung vorrücken wird. Aber weil hier eine Verknüpfung zwischen Dingen derselben Klasse nicht gegeben ist und auch so bei genauer Sprache keine Verknüpfung der Begriffe mit Begriffen gegeben ist, sondern der Klassen mit den Klassen, wird sich die Berechnung der Veränderungen auf die Fragestellung 3 beziehen. Denn weil ja auch die Verknüpfung, die in einer derartigen Stellung ist, kann durch die Scheiben dargestellt werden, wie wir bald erklären werden, hat eine Verwandtschaft erzeugt, dass wir überrascht wären. Deshalb werden wir es so finden: 6 wird mit sich selbst 9 mal multipliziert: 6 · 6 · 6 · 6 · 6 · 6 · 6 · 6 · 6, oder es wird eine geometrische Folge von 6 gesucht, deren Exponent 9 ist, oder die 9. Potenz von 6 macht 18.077.696; so viel größer ist es als Georg Philipp Harsdörffer glaubt, dass es nur 216 Fragen seien.
So oft die übrigen in Verknüpfungen der einzelnen Begriffe in einzelne gezogen werden, dann ist es notwendig so viele Räder zu machen, wie die Zahl der Dinge Einheiten enthält: danach ist es notwendig die einzelnen Rädern mit allen Dingen zu beschreiben. So werden durch verschiedene Drehungen der Räder unzählige Verknüpfungen erzeugt, und alle Verknüpfungen werden jetzt gewissermaßen besonders Schriften sein, welche in der Tat kaum zum Schreiben großer Bücher ausreichen.
Auf diese Weise hat der sehr gelehrte Georg Philipp Harsdörffer in 13. Teil Abschnitt 4 Fragestellung 5 ein Gerät mit 5 konzentrischen Scheiben konstruiert, das er "Fünffachen Denkring der deutschen Sprache" nennt, wo auf dem innersten Ring 48 Vorsilben stehen, auf der vorletzten 60 Anfangs- und Reimbuchstaben, auf der mittleren 12 Mittelbuchstaben, nämlich Vokale oder Diphthonge, auf der zweitletzten 120 Endbuchstaben, auf der äußersten 24 Nachsilben. Er versichert in diesen sind wird die ganze deutsche Sprache aufgelöst. Weil hier die Klassen ähnlich wie die herzuleitenden Klassen, multiplizieren wir 48, 60, 12, 120, 24 das ergibt aus den früheren mit dem folgenden macht 97.209.600. Das ist die Anzahl der hier entstehenden nützlichen Worte der Deutschen ist, oder 96 bedeutende und unbrauchbare.
Auch Ramon Llull hat Räder gebaut, und im Thesaurus der Erinnerungskunst Johann Heinrich Alsted dessen Räder, in denen Dinge und Fragen, angefügt ist die Bewegungsvorschrift, in der die Orte der Schriften, nach denen die Dinge besprochen werden, die Fragen geprüft werden; und die Bruderschaft der Rosenkreuzer verspricht in ihrer Legende ein großes Buch mit dem Titel "Das Rad der Welt", in dem alles Wissen enthalten wäre. Joh. Davidius, Jesuit, fügt einen gewissen Kreislauf der Frömmigkeit, wie er es nennt, seiner Christlicher Wahrheit hinzu. Auf derselben Grundlage der Verknüpfungen berugt die Stäbchenrechnung John Napier, Laird of Merchiston, und die hängenden Riegel, die Vorlegschlösser, die ohne Schlüsse durch wundersame Kunst geöffnet werden, sie nennen sie Mahl-Schlösser, das Gebäude ist nämlich durch Riegelringe verschlossen, gewissermaßen drehbare Ringe, auf die einzelnen Ringe sind Buchstaben des Alphabets geschrieben. Ferner ist dem Riegel ein bestimmter Name zugewiesen, z. B. Ursula, Catharina, in dem Fall wenn wer nicht den Namen kennt, kann der Dreher der Ringe nicht durchdringen. Aber wer den Namen gewusst hat, die Ringe so gegeneinander dreht, dass endlich der Name erschiene, oder die Buchstaben des Alphabets mit dem gegebenen Namen zustande gebracht seien aus den verschiedenen Ringen in der gleichen Linie, in der richtigen Reihenfolge. Dann erst wenn die Ringe in solchem Zustand sein werden, wird er leicht den Rigel öffnen können. Siehe zu diesen Ringriegeln Johann Jacob Wecker in "17 Bücher über Geheimnisse", den sehr bekannten Gustavum Selenum (Pseudonym von August der Jüngere, Herzog zu Braunschweig-Lüneburg, Fürst von Braunschweig-Wolfenbüttel) in "Kryptographie" Blatt 449, Daniel Schwenter in " Deliciae physico-mathematicae oder mathematische und philosophische Erquickstunden", Abschnitt 15, Fragestellung 25. Wir wollen aufhören den Gebrauch der Fragestellungen 1 und 2 aufzuzählen, mit dem Abschluss über Farben den wir besprochen haben. Georg Philipp Harsdörffer behauptet im Teil 3, Abschnitt 3 Vorschlag 16 die Primärfarben sind diese: Weiß, Gelb, Rot, Blau, Schwarz.
Diese legt er doch so zusammen, dass die äußersten: weiß und schwarz sich niemals gleichzeitig vereinigen. Deshalb entsteht aus Weiß und Gelb weißlich, Weiß und Rot fleischfarben, Weiß und Blau aschgrau, Gelb und Rot goldfarben, Gelb und Blau grün, Gelb und Schwarz dunkel, Rot und Blau Purpur, Rot und Schwarz rötlich, Blau und Schwarz dunkelblau. Deshalb sind es 9, so viel sind nämlich Verknüpfungen von 2 der 5 Dinge, ausgenommen eines der äußersten. Was aber wenn Farben der dritten Ordnung zugefügt würden, oder Verknüpfungen von 3 der Grundfarben und Verknüpfungen von 2 der Sekundärfarben, und so weiter, eine wie große Vielzahl wird sich ergeben? Denn ich erinnere mich daran, dass wie die als Grundfarben angesehenen selbst keine Grundfarben sind, sondern alle aus Weiß und Schwarz, oder aus der Mischung von Licht und Schatten entstehen.
Aber ich erinnere mich gelesen zu haben, wenn auch der Autor nicht in den Sinn kommt, welcher edle Seidensticker 80 Farben zusammengewebt hatte, weiß ich nicht, und die benachbarten immer mit Nachbarn verbunden hatte, und von den Fäden dennoch bloß sehr schwarze oder bloß sehr weiße, ferner verschiedene Wechsel der weißen und schwarzen Fäden, und die Unmittelbarkeiten manchmal mehr weißer manchmal mehr schwarzer, eine Verschiedenheit der Farben erzeugt zu haben; die einzelnen Fäden an sich sind dem unbewaffneten Auge aber kaum sichtbar gewesen. Wenn es so ist, wäre das der einzige hinreichende Versuch zur Natur der Farben von ihrem Ursprung an zu wiederholen gewesen.
Fragestellung III.
Aus der gegebenen Anzahl der Klassen und Gegenstände in den Klassen, die Zusammenstellungen in den Klassen zu finden.
"Aber die Verknüpfungen der Klassen sind, deren Exponent mit der Nummer der Klassen dasselbe ist; und durch eine beliebige Verknüpfung aus einer beliebigen Klasse eine Sache ist. Es wird die Anzahl der Dingen einer Klasse mit der Anzahl der anderen Dingen multipliziert; und wenn es mehrere sind, die Zahl des dritten in das Produkt aus diesen, oder immer die folgende Zahl in das Produkt aus den vorhergehenden; das Produkt aus allen zusammenhängenden wird das gesuchte sein."
Der Gebrauch dieser Fragestellung wäre so wie der Gebrauch 6 in der Fragestellung 1 und 2 gewesen, wo wir die Verfahren der Syllogistik untersuchten, ferner im Gebrauch 12, wo sich auch Beispiele anboten. Wir haben oben gesagt, die Lehre der Verknüpfungen ist umzukehren in die Trennung von zu findenden untergeordneten Gattungen, ebenso sind die Arten einer Trennung zu finden, und endlich die meisten der miteinander multiplizierten.
Und dieses haben wir zuletzt für diese Stelle aufbewahrt. Aber eine Teilung ist in ein Unteilbares auszuführen die Glieder einer Trennung eines anderen Gliedes zu unterteilen, was manchmal wechselseitig gelingt, manchmal nicht. Manchmal können alle Glieder einer einzigen Trennung durch alle anderen unterteilt werden, gewisse manchmal so oft, oder durch gewisse so oft. Wenn umgekehrt, werden wir es so bezeichnen:
| ⎧ | c | |||
| ⎧ | a | ⎥ | ||
| A | ⎨ | ⎨ | d | |
| ⎩ | b | ⎥ | ||
| ⎩ | e |
| wenn gewisse mehr, so: | ⎧ | c | |||
| ⎧ | a | ⎨ | d | ||
| A | ⎨ | ⎥ | |||
| ⎩ | b | ⎩ | e |
| wenn gewisse durch gewisse mehr, so: | c | ||||
| ⎨ | |||||
| a | d | ||||
| A | ⎨ | ||||
| b | … | e |
Aber zu unserer Berechnung gehört wenigstens ein erstes Verfahren, in dem ein ausgezeichnetes Beispiel aus der Politik genügt. A soll der Staat sein, a der richtige, b der abweichende, was eine sittliche Einteilung ist; c die Monarchie, d die Aristokratie, e die Republik, welche eine zahlenmäßige Einteilung ist: die zahlenmäßige Einteilung wird mit der sittlichen multipliziert; es entstehen 2 · 3 macht 6 gemischte Arten, ac, ad, ae, bc, bd, be.
Hier liegt der Ursprung dessen Regel: die Teilung mit der Teilung multipliziert ist offensichtlich, denn die Anzahl der Arten des einen ist mit der Anzahl der Arten des anderen zu multiplizieren. Aber die Zahl in einer Zahl zu ziehen ist die Zahl mit der Zahl zu multiplizieren, und ebenso oft zum gegebenen zu stellen, wie viele das andere Einheiten hat. Der Ursprung stammt aus der Geometrie, wo wenn eine Strecke, die eine andere berührt, von Anfang zum Ende bewegt wird, wenn weil sie diese kratzen würde, der gesamte Raum, den die bewegte Strecke einnehmen wird, eine viereckige Figur bildet, wenn sie die andere in einem rechten Winkel schneidet, ein ungleichseitiges [Rechteck] oder ein Quadrat: wenn aber ein andrer [Winkel], eine Raute oder ein Parallelogramm; wenn andere gleich sind ein Quadrat oder eine Raute; wenn aber anders ein ungleichseitiges Viereck oder ein Parallelogramm. Daher ist auch der aus der Multiplikation der Strecke mit der Strecke erstellte rechteckige Raum selbst gleich.
Im Übrigen gibt es zu derartigen faltbaren Trennungen Bücher voll mit Tabellen, und es entstehen manchmal Verwirrungen aus der Vermischung verschiedener Teilung zu einer, was das zu teilende Bewusstsein in rechtes, irrtümliches, mögliches, zweifelhaftes sichtbar macht. Denn zum Verständnis der Wahrheit wird in richtige und irrtümliche getrennt, durch die Überlegung der Bestätigung beim unsicheren, möglichen, zweifelhaften Begreifen; was aber ist Zweifel anderes, als gewissenhaft?
Auch die besondere Untersuchung dieser Fragestellung des Varro bei B. Augustinus im Buch 19 über den Gottesstaat, Kapitel 1, die Zahlen der philosophischen Schulen ist das höchstmögliche Gut. Deshalb werden wir zuerst dessen Berechnung folgen, danach werden wir zu einem genaueren Urteil kommen.
Es gibt VI Einteilungen, die erste ist viergliedrig, die 2. Und 6. dreigliedrig, die übrigen sind zweigliedrig. I. Das höchste Gut kann entweder Lust oder Schmerzlosigkeit sein, oder beides, oder Grundbedürfnis. 4. II. Ein beliebiges derer wird entweder durch Tugend erstrebt, oder die Tugend infolge ihrer selbst, oder sowohl wegen ihrer selbst als auch die Tugend aus sich heraus, 4 · 3 macht 12. III. Irgendein höchstes Gut sucht entweder in sich oder in der Gesellschaft 12 · 2 macht 24. IV. Die Meinung aber zum höchsten Gut beruht entweder auch sicherem Verstehen oder akademischer Möglichkeit. 24 · 2 macht 48. V.Die Lebensart ist zynisch oder kultiviert, 48 · 2 macht 96. VI. Müßig, geschäftig oder gemäßigt, 96 · 3 macht 288. Dies hat Marcus Terentius Varro bei B. Augustinus von Hippo im Kapitel 1 oder 2 nach genauer Zählung festgestellt. Dies hat Marcus Terentius Varro bei B. Augustinus von Hippo im Kapitel 1 oder 2 nach genauer Zählung festgestellt. Er sagt die Teilung macht 3, 5, 6 auf fortgesetzte Weise; 4 auf zu begreifende Weise des höchsten Guts; deshalb fallen die letzten Teilungen zusammen, und die 276 Verschiedenheiten, 12 verbleiben. Weiterhin sagt er im Kapitel 3 Lust, Schmerzlosigkeit und beide sind in den Grundbedürfnissen enthalten. Es verbleiben deshalb 3 (9 fallen zusammen) Grundbedürfnisse an sich, Tugend an sich, und beide an sich. Aber den letzten Satz widmet Marcus Terentius Varro und gleichsam durch eine gemachte Siebung den am Boden verbleibenden.
Zu diesem meine ich, Marcus Terentius Varro hatte nicht so sehr die möglichen Sätze sammeln gewollt, als die bekannten, hier dessen Lehrsätze: welche sich im Bezug auf das Grundbedürfnis unterscheiden, unterscheiden sich durch die philosophische Schule und umgekehrt. Inzwischen hat er nun die Teilung aufgestellt, er hat nicht gekonnt, dass er manche führungslos dazu mischt. Warum er im Übrigen Teilungen hinzugefügt hat, welche er danach nicht eine Änderung der Grundbedürfnisse zu machen anerkennt, ob dass er durch die Anzahl von Unerfahrenen Bewunderung erregt hätte? Außerdem wenn er die Arten des Lebens dazu mischen wollte, warum nicht mehrere? wurden nicht von den einen die Wissenschaften erforscht, von anderen überhaupt nicht; machen andere einen Beruf aus der Weisheit, und glauben durch diese vor allem die Grundbedürfnisse zu erhalten? Auch ist das für das Grundbedürfnis von großer Bedeutung, in welcher Gemeinschaft wer lebt: die einen haben das Landleben dem städtischen vorgezogen, und es werden gewöhnlich unendliche Arten der Veränderungen genannt, in den einzelnen irgendeiner gewesen ist, wer hätte diesem einzigen Weg geglaubt zum Grundbedürfnis gehen zu können.
Ferner wann die erste Teilung mit dem ersten Glied die zweite multipliziert wird ergibt es 4 Arten: 1. die Lust, 2. die Trägheit, 3. Beide, 4, das Grundbedürfnis infolge der Stärke, denn weil in allen ein einziges höchstes Gut ist, die Tugend; wie das Grundbedürfnis, so auch die Übrigen, wie die Lust, so bezieht sich auch die Trägheit auf die Tugend. Füge was in der Möglichkeit Marcus Terentius Varros war hinzu, nicht nur das 2. und das 6., sondern auch das 3. und das 4. und das 5. um das dreigliedrige zu machen, durch Zufügen einer dritten Art, immer aus zweien gemischt; z. B. in sich oder in die Gemeinschaft oder in beide; durch sicheres Begreifen, Mögliches, Zweifel; zynisches, kultiviertes, gemäßigtes.
Es hätte auch einen Lehrsatz gegeben, der leugnet, dass das Grundbedürfnis fortwährend gegeben wird, sondern es ist zu machen, was jedem in den Sinn käme, zu dem er gebracht worden wäre durch die reine und ungehemmte Bewegung. Dieses verkünden die neuen Akademien, und der heutige Geist der Wiedertäufer beugte sich. Wenn aber jene die es leugnen können sie in diesem Leben diesen Gipfel ersteigen? was Solon zur der Ungewissheit es auszusprechen gesagt hat, ist die Natur der Sache selbst der aufgerührten christlichen Philosophen. Valentinus ist Erhard Weigel allerdings zu schwärmerisch, die Glückseligkeit des Menschen ist Vergötterung.
Auch bei denen, von denen die Glückseligkeit des ewigen Lebens aufgestellt wird, stimmen die einen zu, die anderen leugnen die selig machende Vorstellung des Wesens Gottes. Ich erinnere mich dieses machen die Reformierten, und aus diesen ragt die Erörterung über dieses Argument Gisbertus Voetius zwischen ausgewählten heraus; jenes unsere, und für diesen Satz hat Matthias Hoë von Hoënegg ein eigentümliches Büchlein gegen Dekan Václav Budovec z Budova geschrieben.
Auch Marcus Terentius Varro hat in diesem Leben alle jene übergangen, die das Grundbedürfnis als etwas äußeres, dessen was sie Glück nennen, zugrunde legen, das gleiche sei, es ist das Anzeichen die Durchmusterung des Aristoteles selbst. Der Besitz des Körpers gehört gewiss zum obersten Naturbedürfnis, aber kann gemacht werden, dass der eine irgendeiner Gattung dieser sehr mächtigen Lust folgt, ein anderer etwas anderem. Und der Besitz der Seele ist nun entweder ein Zustand oder eine Handlung, jenes die Ansicht der Stoiker, dieses die von Aristoteles. Der durchaus sorgfältige Mann Eckard Leichner, Arzt in Erfurt, hat sich heute den Stoikern angenähert in der Erörterung über die notwendige Erneuerung der Schulen und anderswo.
Dass auch die Lust der Seele für ein Grundbedürfnis zu halten ist meint Lorenzo Valla im Buch über das Wahre Gute, und dessen Schutzrede an Papst Eugen IV, oder Pierre Gassendi in "Die Ethik des Epicurus", und dass dessen Aristoteless VII Nicomachus 12 und 13 vernichtet hat hat der berühmte Jakob Thomasius beobachtet in "Tabellen zur philosophischen Anwendung XXX" Zeile 58. Die Lust der Seele am Ruhm, das ist der innere Triumph der Seele, sich an ihrem Lob zu erfreuen, führt Thomas Hobbes am Anfang der Bücher über den Bürger zurück ("Elementorum Philosophiae Sectio Tertia De Cive." 1642). Sie sind es gewesen, welche die geistige Betrachtung dem Handeln vorzogen, andere im Gegenteil, andere haben beides an den gleichen Platz gestellt. Kurz gesagt, so viele es auch immer Gattungen der Guten gibt, so viele jener Verknüpfungen, so viele Möglichkeiten der Grundbedürfnisse, gibt es philosophische Schulen zu zählen.
Wir werden aus dieser Fragestellung selbst, die Ursprung ist der Anzahl Personen in einem einzelnen Blutverwandtschaftsgrad des Familienstammbaums erforschen, den wir nicht außerordentlich der Höhe unserer Untersuchungen abgewichen zu sein ansehen. Aber zur Berechnung, werden wir das rechtmäßige vernachlässigen, dem bürgerlichen folgen.
Die Nummerierung der Personen in einem Verwandtschaftsgrad ist zweifach, eine allgemeine, die andere besonders. In jener [Zahl] sind so viele Personen wie verschiedene Seitenzweige der Verwandtschaft, in diesem jedoch der Abstand. Aber die Seitenzweige der Verwandtschaft nenne ich gleich wie die Wege im Stammbaum, Linien und Winkel, wenn nur nach oben oder nach unten, oder zur Seite gegangen wird. In dieser macht nicht nur Seitenzweige der Verwandtschaft eine Veränderung, sondern auch das Geschlecht bald der Zwischenglieder, bald der Personen, deren Entfernung gesucht wird von den gegebenen. In jener Nummerierung werden der Onkel, die Tante, das ist Bruder oder die Schwester des Vaters: der Onkel mütterlicherseits, die Tante mütterlicherseits, das ist der Bruder oder die Schwester der Mutter, für die gleiche Person gehalten, und gemeinsam werden sie verstanden unter der Bezeichnung des Onkels, weil die männliche angemessener die weibliche umfasst; aber in der besonderen Nummerierung werden sie für 4 unterschiedliche Personen gehalten. Deshalb werden dort Verwandtschaften, hier Personen nummeriert (denn so dass mehrere Brüder oder mehrere Schwestern, weil sie sich im Geschlecht zwar nicht unterscheiden, für eine von den beiden Personen gehalten werden) jene allgemeine Berechnung ist von Gaius bis zur 1 und 3 Stelle (obgleich es besonders manchmal vermischt ist), diese speziellen von Julius Paulus am wichtigsten jene 10 Stelle in "Digestio de Gradibus et Affinibus". Aber wiewohl es vorher ist in den Fragestellungen 1 und 2 begründet worden, weil es jedoch für das spätere die Grundlage ist, die hierzu gehört, werden wir es vorausschicken.
Verwandtschaft ist die Form der Linie oder der Linien von der verwandten Person zur gegebenen gezogen, aus dem Verhältnis der Geradheit und der Beugung, und deren Veränderung. Eine Person ist hier die Person mit einer gegebenen Verwandtschaft und dem gegebenen Grad, und das Geschlecht bald das eigene bald der dazwischen liegenden, nämlich zwischen der verwandten und der gegebenen. Gegeben aber nenne ich eine Person, der oder die, deren Verwandtschaft gesucht wird wie die alten Rechtsgelehrten es nennen; Johannes Andreae wird berichtet im Namen seines Bidelli genannt zu haben Bruder Franèois Hotman, Seigneur de Villiers-Saint-Pol im Buch über die Grade der Verwandtschaften, hypothetisch, auf Latein These.
Begriff ist eine Person oder Verwandtschaft, die verknüpft ist durch die Vorstellung, z. B. der Bruder ist des Vaters Sohn. Deshalb sind Vater und Sohn Begriffe, aus denen die Vorstellung des Bruders zusammengesetzt wird. Begriffe aber sind entweder Hauptbegriffe, so beschaffene sind allein genau zu bestimmen: Vater und Sohn, wir werden uns jedoch aus dem Grund der bequemeren Berechnung alle Personen in gerader Linie, sowohl nach oben wie nach unten als Hauptbegriffe zugrunde legen, oder gebildete Begriffe; um es genauer zu sagen alle, die mehr als eine Stufe von der gegebenen Person entfernt sind, jedoch entfernter, alle seitlichen so viel. Aber alle seitlichen werden zusammen gesetzt aus den zwei Enden der geraden Linie; daher tritt sehr einfach der Kunstgriff hervor durch die wie auch immer gegebene Verwandtschaft die Zahl des erlangten Verwandtschaftsgrades, z. B. bei der einfachsten seitlichen Person, Bruder oder Vaters Sohn, weil der Vater 1 ist, der Sohn auch im 1 Grad 1 + 1 macht 2, in dem der Bruder ist. Der Rest ist Aufgabe des Schemas. Das soll daher dieses sein:
| Grad. | Verwandtschaften | Gegeben | Person | Gr. | ||||||||||
| 1. | Vater | 2 | 4 | Sohn | 1. | |||||||||
| Vaters | Bruder 1.1 |
Sohn | ||||||||||||
| 2. | Großvater | 3 | 12 | Neffe | 2. | |||||||||
| Onkel 2.1 |
Vetter 1.2 |
|||||||||||||
| 3. | Urgroßvater | 4 | Onkel mütterl. 3.1 |
Vetter 3. Grades mütterl. 2.2 |
Onkel väterl. 1.3 |
32 | Urenkel | 3. | ||||||
| 4. | Ur-Urgroßvater | 5 | Subpropatruus 5.1 |
Subpropatruus Magnus 3.2 |
Subconsobrino 2.3 |
Propatruelis 1.4 |
80 | Abnepos | 4. | |||||
| 5. | Atavi | 6 | 192 | Atnepos | 5. | |||||||||
| Bruder d. Ur-Urgroßvaters 5.1 |
Propatruus 4.1 |
Prosubpatruus Magnus vel Consobrin. secundus 3.3 |
Prosubconsobrinus 2.4 |
Abpatruelis 1.5 |
||||||||||
| 6. | Triavi | 7 | 448 | Trinepos | 6. | |||||||||
In dieser Übersicht gibt es fast unendliche würdige Beobachtung. Wir werden wenige streifen. Personen werden an dem Platz verstanden, wo Punkte sind. Die Punkte einschließenden Zahlen bezeichnen die Enden oder den Grad der geraden Linien (vorhergehend aufsteigende, nachfolgend absteigende) aus denen der seitliche Grad zusammengesetzt wird. In derselben seitlich gerichteten Linie sind die gleichen Verwandtschaftsgrade angeordnet: schräg vom obersten zum untersten, nach rechts in der Reihe der Generationen, aber nach links sind die gleichmäßigen Verwandtschaften mit verschiedenem Grad erfasst. Die einzige senkrechte Linie von der Spitze zur Grundlinie, die das Dreieck teilt, enthält Verwandtschaften, deren Begriffe sowohl auf- wie absteigend, vom gleichen Grade; solche nenne ich gleichgewichtig, und sie werden nur in entsprechenden bezeichneten Zahlen gegeben, in einer bloß einen.
Denn wenn man sich eine Waage vorstellt, deren Zünglein sei eine Linie des ersten Grades, aber Arme seien, rechts freilich, eine senkrechte Linie von der obersten Person absteigende; die Linken aber, senkrecht von der höchsten ansteigend gezogen zum letzten entweder ansteigenden oder absteigenden die gegebenen Verwandtschaft anordnend; sodann von den gleichen Armen, wenn von beiden Seiten 3.3 oder 2.2 usw. wäre die Verwandtschaft im Gleichgewicht und in die Mitte des Dreiecks zu setzen; bei ungleichgewichtigen, ist die Verwandtschaft so zu setzen in jenem seitlichen dass die gerade Linie entweder des an- oder absteigenden, aus dem der längere Arm genommen ist, es ist benachbart.
Hier nun spiegelt sich die Macht der Verbindungen sehr deutlich. Denn es werden alle seitlichen Personen aus 2 Enden zusammengesetzt, von einer Verwandtschaft in gerade aufsteigender Linie, eine andere absteigend, aber immer so, dass sie im Fall des seitlichen Aufstieg, im absteigenden Falle gerade verbunden würden, z. B. der Bruder, das ist der Sohn des Vaters. Aber wenn im Gegenteil, wird er zur gegebenen Person zurück gehen, denn wer sich den Vater seines Sohnes nennt, nennt sich, weil ein Vater mehrere Söhne haben kann, nicht umgekehrt.
Aus dem wird schon gegeben: von jedem vorgegebenen Grad der Verwandtschaften, bald die Zahl, bald die Art zu finden; die Zahl der seitlichen wird immer um eine Gradeinheit kleiner sein (die Zahl aller ist immer um die Einheit) größer, weil sie immer zwei Verwandtschaften der geraden Linie dazugezählt werden müssen, eine oberhalb, die andere darunter) deren Verhältnis aus der Erfindung der Arten offenbar sein wird. "Denn die Verbindung von 2 Teilen, oder Zerlegung in zwei Teile, jeder gegebenen Zahl sind so viele, wie die gegebene Zahl Einheiten hat die halbe geradzahlige, die ungeradzahlige die Hälfte der um die Einheit verringerten, z. B. 6 hat diese: 5, 1, 4, 2, 3, 3, und das Verhältnis dieser Sache ist offensichtlich, weil immer die vorhergehende Zahl nächst der gegebenen mit der entferntesten, gänzlich die nächste mit gänzlich der entferntesten verwoben wird u. s. w." Aber weil hier nicht nur der Verknüpfung, sondern auch der eingenommenen Stellung zu beachten wäre, z. B. ist 5.1, nämlich Urgroßvater, eine andere Verwandtschaft als 1.5, nämlich Großcousin, weil hier 2 Dinge die Stellung durch 2 Vertauschungen wechseln. Also werden die Zerlegungen verdoppelt, es wird die gegebene Zahl zurückgegeben werden, wenn sie geradzahlig gewesen war, aber weil in deren Zerlegungen eine gleichmäßige geben würde, z. B. 3.3 in der nichts die Anordnung ändert, wird sie hier von der gegebenen Zahl abgezogen, oder die Zerlegung vom Doppelten, wiederum 1. Wenn aber die gegebene Zahl ungerade gewesen ist, ergibt es die Zahl um 1 kleiner.
Aus diesem ist allgemein offensichtlich: (1) Wird die Einheit von der Zahl des Verwandtschaftsgrads abgezogen, wird das Ergebnis die Zahl der seitlichen Verwandtschaft sein; (2) zwei Zahlen, die sich komplementär sind zur gegebenen, oder deren eine so viel von 1 entfernt ist, wie die andere von der gegebenen, zusammen gesetzt werden sie die Art der Verwandtschaft ergeben, wenn allerdings die vorhergehende verstanden wird den ansteigenden anzuzeigen, folgend seinem absteigenden Grad. Bei dieser Gelegenheit wird nebenbei erklärt, was die möglichen Zerlegungen der gegebenen Zahlen wären.
Denn zwar sind alle Zerlegungen Verknüpfungen, aber der Verknüpfungen derer sind bloß Zerlegungen, die gleichzeitig alle gleiche sind. Ähnlich können sie angeregt werden, bald die Verknüpfungen von 2, bald die Verknüpfungen von 3, bald die einfachen Zerlegungen, bald durch den gegebenen Exponenten. Wie viele Faktoren oder Divisoren irgendeine gegebene Zahl genau hätte, verstehe ich als gewöhnlich gelöst. Und hier ist was Plato die Zahl der Bürger zu sein gewollt hat 5.040, weil diese Zahl sehr viele Teilungen der Bürger zu lässt für die Arten der Ämter, nämlich 60, Buch 5, Seite 845 über die Gesetze. Und von diesem zwar bei der Vervielfältigung und Teilung, aber wer durch Addition um die Veränderungen der gegebenen Zahl zu bewirken, und durch Subtraktion um zu Zerteilen hergeleitet hätte, was beide von demselben hat er verkürzt, es ist mir nicht bekannt. Aber den Weg der Zerteilungen die Verknüpfungen von 2 herzuleiten zeigen wir als nächstes. Aber wenn mehrere Teile zugelassen werden, wird ein gewaltiger Abgrund der Zerteilung eröffnet, in welchem uns offenbar wird eine gewisse Grundlage der Berechnung zu erkennen, denn immer entstehen Zerteilungen in 3 Teile aus den Zerteilungen in 2, bevorzugt eine; das auszuführen ist aber an dieser hier nicht die Zeit.
Bevor wir übrigens in unserem Stammbaum von der allgemeinen Berechnung zur speziellen kämen, ist an dieser Stelle daran zu erinnern, dass die von uns den Verwandtschaften zugewiesenen Definitionen nicht im allgemeinen Gebrauch sind. Denn z. B. definiert niemand den Onkel als Sohn des Großvaters, sondern eher als Bruder des Vaters. Wer auch immer deshalb diese Definitionen zur gewöhnlichen Sitte gestalten wollte, wenn allerdings eine Person schräg aufsteigt, setzt er an Stelle des absteigenden Begriffs für Sohn den Vater, für Enkel Großvater u. s. w. an Stelle des Absteigenden setzt er den einen Grad kleineren; wenn er aufsteigt umgekehrt.
Weil wir jetzt gezeigt haben, dass die Verwandtschaften in einem beliebigen Grad, durch die um 1 größere Zahl des Grades ist, verschiebe auch die Personen der Verwandtschaften die wir zählen würden, welches die besondere Nummerierung ist. Wir haben aber gesagt in ebender Verwandtschaft einen Unterschied zu machen, bald durch Verbinden mit dem Geschlecht, bald der zwischen den Verwandten und den gegebenen Personen liegenden. Es gibt aber zwei Geschlechter. Deshalb muss immer fortlaufend die Zahl der Personen verdoppelt werden, z. B. nicht nur unterscheiden sich Vater und Mutter durch das Geschlecht, 2, sondern der Vater hat wiederum Vater oder Mutter. Und die Mutter auch, deshalb 4. Der Großvater hat auch vom Vater den Vater und die Mutter, und die Großmutter vom Vater, und der Großvater von der Mutter und Großmutter genauso; deshalb 8 u. s. w. Deshalb leite ich Regel ab: "2 wird so oft mit sich selbst multipliziert, wie der Grad der Person die gesucht ist, oder was dasselbe ist, gesucht wird die Zahl der geometrischen Folge von 2, deren Exponent die Zahl des Grades ist. Diese wird multipliziert mit der Zahl des gegebenen Grads der Verwandtschaften; die Zahl der Personen des gegebenen Grades wird erzeugt."
Und nach diesem Verfahren habe ich die Anzahl der Personen ermittelt, die der Rechtsgelehrte Julius Paulus am angegebenen Ort 10 mit Ausnahme von Grad 5. Grad 1: 2 · 2 macht 4 stimmt mit Julius Paulus am angegebenen Ort 10 § 12 überein. Grad II: 2 · 2 macht 4 · 3 macht 12 § 13. Grad III: 2 · 2 · 2 macht 8 · 4 macht 32 § 14. Grad IV: 2 · 2 · 2 · 2 macht 16 · 5 macht 80, § 15. Gard V: 2 · 2 · 2 · 2 · 2 macht 32 · 6 macht 192, das widerspricht Julius Paulus im § 16 er behauptet 184, dessen Berechnung jedoch einen Fehler enthalten muss. Grad VI: 2 · 2 · 2 · 2 · 2 · 2 macht 64 · 7 macht 447 stimmt mit Julius Paulus § 17 überein. Grad VII: 2 · 2 · 2 · 2 · 2 · 2 · 2 macht 128 · 8 macht 1024, am Ende von § 18.
Fragestellung IV.
Aus der gegebenen Anzahl Gegenstände die Veränderungen der Anordnung zu finden.
| 1 | 1 |
| 2 | 2 |
| 6 | 3 |
| 24 | 4 |
| 120 | 5 |
| 720 | 6 |
| 5.040 | 7 |
| 40.320 | 8 |
| 362.880 | 9 |
| 3.628.800 | 10 |
| 39.916.800 | 11 |
| 479.001.600 | 12 |
| 6.227.020.800 | 13 |
| 87.178.291.200 | 14 |
| 1.307.874.368.000 | 15 |
| 20.922.789.888.000 | 16 |
| 355.687.428.096.000 | 17 |
| 6.402.373.705.728.000 | 18 |
| 121.645.100.408.832.000 | 19 |
| 2.432.902.008.176.640.000 | 20 |
| 51.090.942.171.709.440.000 | 21 |
| 1.124.000.727.777.607.680.000 | 22 |
| 15.852.016.738.884.976.640.000 | 23 |
| 620.448.401.733.239.439.360.000 | 24 |
Die Lösung: alle Zahlen von der Eins bis zur Anzahl der Dinge einschließlich werden in der natürlichen Folge aufgestellt: gemacht aus allen ununterbrochen, die Frage wird sein, wie: es soll sein wie in Tabelle ה die wir bis zur Zahl 24 fortgesetzt haben. Die rechte Spalte hat die Exponenten, oder Anzahl der Dingen, die hier zusammenfallen; in der Mitte sind die Veränderungen selbst. Zur Linken angeordnet ist der Unterschied der Veränderungen der beiden nebenstehenden, zwischen die sie angeordnet ist. Gleich wie der rechts angeordnete Exponent das Verhältnis ist der gegebenen Veränderung zum vorhergehenden. Die Berechnung der Lösung wird offensichtlich sein, wenn wir die Veränderung des gegebenen Exponenten gezeigt haben werden, gemacht aus der Herleitung des Exponenten selbst in der vorhergehenden Veränderung, das ist die Grundlage der Tabelle ה. Zu diesem Ende soll ein anderes Schema ו. In dem wir vor Augen geführt haben, dass die 4 Dinge ABCD sie 24 Veränderungen der Ordnung haben. Die Punkte bedeuten die vorhergehende Sache, die direkt darübersteht. Wir sind dem Verfahren der Anordnung gefolgt, dass zuerst was am wenigsten verändert wird, solange bis nach und nach alles. Übrigens haben wir die Veränderungen des vorangegangenen Exponenten geradezu durch die Grenzen unterschieden von denen was man zufügt folgt. Deswegen in Kürze: jedes Mal wenn sie verändert werden, die gegebenen Dinge, z. B. drei sechsmal: außerdem wird er gesetzt werden können eine hinzugefügt von den beobachteten Veränderungen zur vorigen Zahl bald der ersten, bald der zweiten, bald der dritten, bald der letzten oder dem vierten Platz; oder allesamt wird er können den vorigen verschiedentlich hinzugefügt werden, wie viele er Einheiten habe; Und jedes Mal wird dem vorigen zugefügt alles was er den vorigen Veränderungen aufstellt. Oder so eine beliebige Sache einmal einen Platz einnehmen wird, weil inzwischen die übrigen eine vorangehende Veränderung unter einander haben, vergleiche Fragestellung 7. Es ist deswegen offenbar, dass die vorigen Veränderungen in den folgenden Exponenten zu ziehen sind. Ich beachte hier die folgenden Lehrsätze: 1) alle der Anzahl der Veränderungen sind geradzahlig; 2) aber alle deren Exponent nicht über 5 ist gehen in Ziffern zu ende, sogar in so vielen Ziffern, wie oft der Exponent 5 enthält 3) Alle der höchsten Veränderungen sind ungerade (das heißt die Zusammengesetzten der Veränderungen von 1 bis irgendwohin); und enden in 3 von 4 Exponenten im Unendlichen. 4) welche Veränderung auch immer vorangeht, wie auch deren Exponent misst alle nachfolgenden Veränderungen.
| A | b | c d |
| • | • | d c |
| • | c | b d |
| • | • | b d |
| • | d | b c |
| • | • | c b |
| B | a | c d |
| • | • | d c |
| • | c | a d |
| • | • | d a |
| • | d | a c |
| • | • | c a |
| C | b | a d |
| • | • | d a |
| • | a | b d |
| • | • | d b |
| • | d | b a |
| • | • | a b |
| D | b | c a |
| • | • | a c |
| • | c | b a |
| • | • | a b |
| • | a | b c |
| • | • | c b |
5) die Anzahlen der Veränderungen bilden bei Umwandlung zur harmonischen arithmetischen Reihe. Denn es sei die arithmetischen Reihe 1, 2, 3, 4, 6 in eine stete umzuwandeln: die größte Zahl, an dieser Stelle 5 die Veränderung ist gesucht: 120, diese wird durch ein die einzelnen geteilt, erzeugen sie 120, 60, 40, 30, 24, die Glieder der harmonischen Reihe. Durch die wenn die gleiche Zahl 120 geteilt wird, die Zahlen kehren zu deren arithmetische Reihe zurück. 6) Wenn irgendeine gegebene Veränderung verdoppelt wird, vom erhaltenen Produkt abgezogen wird aus dem Produkt des unmittelbar vorhergehenden mit seinem Exponenten, wird der Rest die : Summe der beiden Veränderungen sein, z. B. 24*2 macht48 — 6*3, 18, macht 30 = 6+24 macht 30. 7) Eine gegebene Veränderung mit sich selbst multipliziert, den Faktor durch den vorhergehenden geteilt, wird die Differenz zwischen der gegebenen und der folgenden ergeben, z. B. 6*6 macht 36 : 2 macht 18 = 24-6 macht 18. Besonders die beiden letzten Lehrsätze hätte ich aber dagegen nicht leicht geglaubt. Wenn auch der Gebrauch vielfältig ist, doch ist uns die gestellte Aufgabe, dass wir nicht allen übrigen Fragestellungen vorgriffen. Und weil wir besonders die ernsthaften Anwendungen der Schlussfolgerungen der Lehre vermischten (denn es war oft notwendig die Veränderungen der Reihenfolge in Schlussfolgerungen zu ziehen), werden sie hier zum größten Teil mehr erfreulich als nützlich sein. Folglich fragen sie, wie oft könnten sich wie viele auch immer gegebene Personen an einem Tisch n der einen oder anderen Ordnung niederlassen. Jeremias Drexel in Der Kreis des Phaeton oder die Fehler der Sprache, Seite 3 c. l. wo er über die sorglose Sprache die Fabel so erzählt: Der Familienvater, ich weiß nicht wer, hatte 6 Gäste zum Gastmahl geladen. Diese weil es Zeit war sich zum Essen zu setzen, übertragen sie einander gegenseitig den Ehrenplatz, er ermunterte sie so: ob sie im Stehen die Speisen einnehmen wollten? allerdings das nicht so, weil auch im Stehen eine Reihenfolge nötig ist. Wenn ihr nicht aufhört, dann werde ich euch, damit ihr euch nicht beschweren könnt, so oft ich zum Mahl rufen werden, jedes Mal die Reihenfolge geändert werden kann. Nachdem er dies gesagt hätte, hat er nicht geruht die gewissenhafte Berechnung, denn so hatte er 720 Veränderungen in Erfahrung gebracht (denn so viele gehören zu 6 Exponenten, wie Jeremias Drexel auf 12 Seiten mit je 3 Spalten und jeder Spalte 20 Veränderungen vor Augen geführt hat) so viele Gastmahle müsste er ausrichten; was wenn er sie fortlaufend ausrichtete, 720 Tage, das sind 10 mehr als 2 Jahre brauchen würde. Georg Philipp Harsdörffer setzt in Deliciae physico-mathematicae oder mathematische und philosophische Erquickstunden Seite 2, Absatz 1 Fragestellung 32 die Gästezahl auf 7; so werden die Tage des Gastmahls 5.040 sein, das sind 17 Jahre und 10 Wochen. Aber Georg Henisch, Arzt in Augsburg, in Arithmetica perfecta et demonstrata, doctrinam de numero triplici, vulgari, cossico et astronomico noua methodo per propositiones explicatam : continens libris septem Buch 7, Seite 399, setzt 12 Gäste oder Tischgenossen ein; die erzeugen 479.001.600 Veränderungen, Gastmahle, Tage; die brauchen 1.312.333 Jahre und 5 Tage. Sogar wenn wer dies im Exponenten versuchen wollen würde, was Jeremias Drexel mit der Hälfte derer bewirkte, nämlich die Veränderungen vor Augen zu prüfen, würde er 100 Jahre aufwenden, davon ein Viertel genommen, und wenn er am Tag 12 Stunden arbeiten würde und in jeder Stunde 1.000 Veränderungen schaffen würde. Der Wert der Arbeit gefällt den Göttern! Andere, dass sie die Übersättigung der bloßen Betrachtung gleichsam würzen würden arbeiten Verse aus, die unversehrt sowohl durch Verständnis, als auch durch Versmaß und Worte auf verschiedene Weise angeordnet werden können. Solche nennt zuerst Julius Caesar Scaliger im 2. Buch Proteus Dichter. Deren halten andere für weniger Kunst, mehr für Veränderungen, diese nämlich deren alle ist eine Veränderung einsilbiger; andere dagegen, in denen die rechte Mischung der einsilbigen und der anderen ist. Und weil ja gewöhnlich in diesen viele unbrauchbare Veränderungen sind, die am Orte der Fragestellung 11 und 12 zu betrachten sind, werden wir nun über diese einzigen sprechen. Bernardus Bauhusius, ein Jesuit und ein angesehener Künstler der Sinngedichte, durch solche Hexameter unseres Heilands zum Beispiel die Titel Einsilbige wird es verstanden:
- Rex, Dux, Sol, Lex, Lux, Fons, Spes, Pax, Mons, Petra
CHRISTUS
Diesen Erycius Puteanus in Wunder der Frömmigkeit, Seite 107, und andere sagen dass es 362.680 Mal verändert werden kann, man kann die Einsilbigen so viele berücksichtigend, welche 9 sind; ich erachte die Anzahl fast 10 mal größer zu sein, nämlich diese 3.628.800. Denn die zehnte Betonung einbeziehend kann auch Christus überall gesetzt werden, wenn nur Petra unbeweglich bleibt, und nach Petra oder die Betonung Christus oder 2 einsilbige gesetzt werden. Es gibt deswegen unbrauchbare Veränderungen, von welchen nach Petra gesetzt wird 1 einsilbiges als nächstes zum vorhergehenden Petra Christus; das trifft zu für 8 einsilbige die so oft Veränderungen sind, nämlich 40.320 mal, weil man am Ende was auch immer aus jenen 9 sein kann. 40.320*9 macht 362.880-3628800 macht 3.265.920, was die Anzahl der brauchbaren Verse dieser Veränderungen von Bernardus Bauhusius ist. Thomas Lansius aber hat mit ansehnlichem Fortschritt im Vorwort der Consultationen bearbeitet was folgt:
- Lex, Rex, Grex, Res, Spes, Jus, Thus, Sal, Sol (bona), Lux, Laus.
- Mars, Mors, Sors, Lis, Vis, Styx, Pus, Nox, Fex (mala), Crux, Fraus.
Hier können in einem einzigen Vers, weil er 11 einsilbige enthält, 39.916.800 Wechsel verändert werden. Deren durch Beispiel hat Heinrich Christoph Ebell aus Gießen, einst Rektor der Schule in Ulm, zuerst Hexameter, danach elegische Distichon ersonnen. Dieser ragt hervor im Vorwort Nr. VIII, weil er auch zurückläuft, in seinem Werk der Vers-Palindrome, welche er gesammelt in einem Bändchen im Jahr 1623 in Ulm im Format Duodez herausgegeben hat. So hat er Hexameter:
- DIs, VIs, LIs, LaUs, fraUs, stirps, frons, Mars, regnat In orbe.
Wo das gleiche Werk das sowohl zusammengestellt wurde als auch wirklich wiedergegeben wird im 1620. Jahre nach Christi Geburt. Weil dieses 8 einsilbige enthält, ist es nötig, dass 40.320 Veränderungen entstehen. Aber das Distichon an den Heiland ist so beschaffen:
- Dux mihi tu, mihi tu Lux, tu Lex, Jesule, tu Rex : Jesule tu Pax, tu Fax mihi, tu mihi Vox.
Die Veränderungen werden wir so berechnen: der Inschrift des Heilands sind 7 einsilbige diese werden untereinander durch 5.040 Wechsel verändert. Und weil eine einzelne Betonung benachbart ist dem Tu (Dich), was mit seiner Inschrift durch 2 Wechsel verändert wird, weil es bald davor, bald danach gesetzt werden kann, und das erreicht durch 7 Wechsel, wird zweimal siebenmal in sich gezogen, 2, 2, 2, 2, 2, 2 *2 macht 128 oder die 7. Potenz von 2, multipliziert mit 5.040*128 macht 645.120; das Produkt ist das gesuchte. Diese wollte dass sie auch unter seinem Namen Giovanni Battista Riccioli gelesen werden, damit die mit seinem Werk zur Dichtkunst die Fähigkeit des Lehrers einst auf ihn so sehr heller aufleuchteten. Dessen Bekenntnisse in Neuen Almagest Teil I Buch 6 Kapitel 6 Anmerkung 1 Blatt 413 folgen:
- Hoc metri tibi eo me nunc hic, Thety, Protea sacro:
Sum Stryx, Glis, Grus, Sphynx, Mus, Lynx, Sus, Bos, Caper et Hydrus.
Dessen 9 einsilbige werden durch 362.880 Wechsel verändert. Wenn man anstelle der letzten Betonungen: et Hydrus, einsilbige einsetzt, z. B. Lar, Grex, hätte er sich zu den Veränderungen von Thomas Lansius aufgeschwungen. Hier sehe ich mich gezwungen zu erinnern, damit er mich nicht auch die Ansteckung des Vorwurfs züchtigt, die erste verdorbene Thetys (Meeresgöttin) habe ich nicht gelesen. Und es kommt bei dieser Gelegenheit jener Marcus Pedo Vergilianus in den Sinn. Georgicon Buch 1, Vers 31.
- Teque sibi generum Thetys emat omnibus undis.
Denn den einen ist Thetys die Königin des Meeres, Gefährtin der Nereiden; den anderen eine gemeine Meeresnymphe, dem sterblichen Peleus angetraut, Mutter des Achill, und nicht würdig dem der dich Proteus verehrt. Diese wird gewiss getadelt:
- Vecta est frenato caerula pisce Thetys.
Übrigens hat Giovanni Battista Riccioli den Julius Caesar Scaliger nachahmen wollen, denn beide haben einen Proteus-Vers über Proteus.
- Perfide sperasti divos te fallere Proteu.
Über dessen Veränderungen in der letzten Fragestellung unten. Damit die Deutschen nicht als geringer gesehen würden, hat sich Georg Philipp Harsdörffer der Ausarbeitung unterzogen, in dessen " Deliciae physico-mathematicae oder mathematische und philosophische Erquickstunden" ragt der Zweizeiler hervor:
- Ehr, Kunst, Geld, Guth, Lob Weib und Kind
- Man hat, sucht, fehlt, hofft und verschwind.
Dessen 11 Einsilber haben 39.916.800 Veränderungen. So viel zu Versen. Aber obgleich auch Annagramme hierzu gehören, welche nicht anderes sind als brauchbare Veränderungen der gegebenen Buchstaben der Rede, doch wollen wir nicht die üblichen Bücherschränke ausschlachten. Einen Streitfall der Berechnungen aus der Literatur ist es sogar wert zu untersuchen: wie viele unterschiedlich Stellen der Buchstaben im Alphabet es gäbe. Christophorus Clavius hat in "In Sphaeram Ioannis de Sacro Bosco commentarius", Kapitel 1 Seite 46 gesagt, die 23 Buschstaben der lateinischen Sprache haben 25.852.016.738.884.976.640.000 verschiedene Anordnungen, das stimmt mit unserer Berechnung überein; den 24 Buchstaben der deutschen Sprache weist Johann Lauremberg 620.448.397.827.051.993 Veränderungen zu. Erycius Puteanus im genannten Büchlein 62.044.801.733.239.439.360.000. Aber Henricus ab Etten 620.448.593.438.860.613.360.000, alle gerecht zu wenige. Die wahre Anzahl ist, wie in Tabelle ח gezeigt, ist hier: 620.448.401.733.239.439.360.000. Alle stimmen darin überein, dass die ersten Ziffern 620.448 sind. Der Irrtum der Berechnungen von Erycius Puteanus liegt nicht im Verständnis, sondern wird als Schreib- oder Druckfehler gesehen, denn nichts anderes, als am siebenten Platz fehlt die Ziffer 4. (Aber das eine sind Veränderungen, das andere die Anzahl der Betonung aus den gegebenen zusammensetzbaren Buchstaben. Denn was ist die Betonung der 23 Buchstaben? Allerdings wie groß sie sei, alle Zusammenstellungen der 23 Dinge würden gefunden werden, in einzelnen Veränderungen würden sie entsprechend Fragestellung 2, Nummer 59, geschlossen werden, Aber die es enthalten zu finden lehrt die Fragestellung 6.) Ferner wie groß diese Zahl ist, dass, wenn auch die gesamte feste Erdkugel ringsherum wäre, und im beliebigen Raumsegment der Mensch auftrat, alljährlich, sogar würden zur einzelnen Stunde alle neu gewählten vergehen, die Summe aller vom Beginn der Welt bis zum Ende würde vieles fehlen, wie Georg Philipp Harsdörffer neulich sagt über Hegiam Olynthium Graecum gezählt haben. Durch diese Überlegungen weil neulich irgendein Freund entgegnet hätte, so folgt, dass es ein Buch sein könnte, in dem alles geschriebene und zu schreibenden gefunden wird: dann bekenne auch ich, frage ich, aber dem bedeutenden Leser das Werk eine wichtige Stütze ist, aber ich fürchte dass er nicht den Erdkreis überrascht. Denn du wirst nicht einfach das Pult gefunden haben durch das Horn jener Tiere, durch die Mohammed in den Himmel getragen das Geheimnis der Dinge erforscht hat, deren Größe und Verschiedenheit seit Zeiten durch das Orakel des Korans gelehrt haben. Alle Sprachen entstehen aus wenigen Buchstaben um den Ursprung der Dinge zu erklären wie es zum Beispiel aus Atomen gebräuchlich ist nach der Lehre des Demokrit von Abdera selbst Aristoteles im 1. Von " Über das Entstehen und das Vergehen", 5. Abschnitt und im berühmten Buch 1. "Metaphysica" Kapitel 4, wo er nach Demokrit von Abdera sagt, die Atome unterscheiden sich durch die Gestalt, das ist die Form, wie die Buchstaben A und N, die These, das ist die Stellung, wie die Buchstaben N und Z denn wenn man von der Seite schaute, wird das eine ins andere verwandelt; die Anordnung, das ist die Reihenfolge, z. B. die Silben AN und NA. Titus Lucretius Carus besingt es auch im 2. Buch so:
- Quin etiam refert nostris in versibus ipsis
- Cum quibus (complexiones} et quali sint ordine (variatio situs) quaeque locata
- Namque eadem coelum, mare, terras, flumina, Solem
- Significant: eadem fruges, arbusta, animantes:
- Si non omnia sint, al multo maxima pars est
- Consimilis; verum positura discrepitant haec.
- Sic ipsis in rebus item jam materiai
- Intervalla, viae, connexus, pondera, plagae,
- Concursus, motus, ordo, positura figura
- Cum permutantur, motuari res quoque debent.
Lucius Caecilius Firmianus Lactantius im 3. Buch der " Institutiones Divinae" (Göttliche Unterweisungen), Kapitel 19, Seite 163: Durch verschiedene Folgen, fragt Epikur, oder Stellungen kommen die Atome gleich wie die Buchstaben zusammen, die weil sie wenige sind, dennoch verschiedentlich unzählige angeordnete Wörter hervorbringen. Füge dazu Diogenes Laertios in Pierre Gassendi" Compendium vitae philosophorum" im 10. Buch herausgegeben in Lyon im Jahr 1648, Blatt 227, und Johann Chrysostom Magnenus " Democritus reviviscens sive de atomis. Addita est vita Democrit" Abhandlung 2 über Atome Kapitel 2 Satz 32 Seite 269. Schließlich gehört zu dieser Umstellung der Buchstaben ein Spiel diese Art zu lehren, das Sophronius Eusebius Hieronymus an Paula von Rom erinnert hat, von Knäblein zur Benutzung von Mosaiksteinen mit eingeprägten Buchstaben und Silben. Das richtet Georg Philipp Harsdörffer im Deliciae physico-mathematicae oder mathematische und philosophische Erquickstunden Teil 2, Abschnitt 13, Satz 3 so ein: man nimmt 6 Würfel, jeder Würfel hat 6 Seiten, und die 36 werden beschrieben, nämlich so: I. a. e. i. o. u. y. II. b. c. d. f. g. h. III. k. l. m. n. p. q. IV. r. s. ß t. w. x. V. v. j. s. r. ä. ö. VI ff. ss. tz. sch. ch. z. Das Alphabet aber des Spiels des einzelnen Mosaiksteins, Silben zweier wird lehren das Buchstabieren: daraus werden nach und nach Worte.
Fragestellung V.
Aus der gegebenen Anzahl Gegenstände die Veränderungen des Platzes nur der auf einander bezogenen oder die Nachbarschaft zu finden.
"Suchte man die Veränderung der unanhängigen Stellung, oder der Reihenfolge, von der kleineren Einheit Anzahl Dinge die gegeben ist, der Fragestellung 4 zufolge, was gefunden wird in Tabelle ה wird das gesuchte sein.". Die offensichtliche Schlußfolgerung der Lösung ist im Schema ו, wodurch wir die Schlussfolgerung der Lösung der voreangegangenen Fragestellung geben werden, z. B. bei Veränderungen der Nachbarschaft, werden die Veränderungen diese: Abcd, BcDA, CDAB, Dabc, für eine genommen, gleichwie im Kreis geschrieben. Und ähnlich mit den übrigen; deshalb sind jene 24 Veränderungen durch die Anzahl der Dinge zu teilen, die hier 4 ist, das wird die Anzahl der Veränderungen der Reihenfolge der vorhergehenden Dinge ergeben, nämlich 6. Stelle dir einen runden Wärmeraum vor der in allen 4 Himmelsrichtungen Zugänge hat, und in der Mitte ist ein Tisch aufgestellt (welches in diesem Fall der ehrenvollste Platz ist erörtert Daniel Schwenter, und hat sich für den Zugang entschieden der nach Osten schaut, von dessen Richtung sei der geehrteste Gast anzuordnen. Deliciae physico-mathematicae oder mathematische und philosophische Erquickstunden Teil VII, Frage 28.) und zwar so die Ordnung der Gäste zu verändern erwogen durch die Überlegung des Vorrangs und des Nachrangs entfernt. Hier werden wir bei der vollkommenen Darstellung zugleich etwas über den Kreis erklären. Weil alle Vordersätze umkehrbar sind, werden 6 Syllogismen entstehen, drei des Kreises. Das soll der Beweis sein:
-
O. gelehrig sein ist vernünftig.
O. Der Mensch ist vernünftig.
E. O. Der Mensch ist gelehrig. -
O. Der Mensch ist gelehrig.
O. vernünftig ist der Mensch.
E. O. Vernünftig sein ist gelehrig. -
O. Der Mensch ist vernünftig.
O. gelehrig ist der Mensch.
E. O. gelehrig sein ist vernünftig. -
O. gelehrig ist vernünftig.
O. Der Mensch ist gelehrig.
E. O. Der Mensch ist vernünftig. -
O. Der Mensch ist gelehrig.
O. vernünftig ist der Mensch.
E. O. vernünftig ist gelehrig. -
O. vernünftig ist gelehrig.
O. Der Mensch ist vernünftig.
E. O. Der Mensch ist gelehrig.
Fragestellung VI.
Bei gegebener Anzahl der zu verändernden Dinge, welche irgendeiner oder irgendwelchen wiederholt werden, die Änderung der Anordnung zu finden.
"Würden die einfachen Dinge gezählt und aus diesen widerholten immer bloß eine, und bei Änderung der Zahlen die gegebene Anzahl der Änderungen durch die Einheit der kleineren; wäre das Ergebnis gesucht. Es seinen z. B. sechs: a, b, c, c, d, e, so sind 4+1 einfache (zwei von den c werden 1 gesetzt) macht 5 * 120 (120=5! aber ist die Änderung der Anzahl 5 aus den ursprünglich gegebenen 6) macht 600. Diese Überlegung ist offensichtlich, wenn man das Schema וּ betrachtet; es fallen nämlich alle Änderungen zusammen, von denen das Ding auf sich selbst gelegt wird. Den Gebrauch werden wir jetzt zeigen. Es soll die Aufgabe sein: aus einem gegebenen Thema alle möglichen Melodien zu finden. Das hat Georg Philipp Harsdörffer in seinen " Deliciae physico-mathematicae oder mathematische und philosophische Erquickstunden", Abschnitt 4, Fragestellung 7 versucht. Aber dieser glaubt im Thema von 5 Silben sind nur 120 mögliche Melodien; er hat einzig die Änderungen der Anordnung betrachtet. Aber uns erscheint es notwendig auch die Zusammenstellungen zu betrachten, wie nun ersichtlich wird. Aber wir werden höheres beginnen: das Thema ist entweder einfach oder zusammengesetzt. Das Zusammengesetzte nenne ich unterschieden in Linien, Reimzeilen. Und die Änderung des zusammengesetzten Themas werden wir durch Melodien der einfachen erforschen, die ununterbrochen in sich gezogen werden mit der Fragestellung 3. Das einfache Thema übertrifft entweder 6 Silben aus oder nicht. Diese Unterscheidung ist deswegen nötig, weil es 6 Tonlagen gibt: Ut, Re, Mi, Fa, Sol, La (wenn ich die 7. Weglasse; Bi, die Erycius Puteanus in seiner Musiktheorie "Musathena, sive notarum heptas" dazu fügt). Wenn es nicht 6 übersteigt, entweder 6 Silben oder es ist kleiner. Wir werden in unserem Beispiel werden wir für den sechssilbigen Themen überlegen, kann man diese Dinge verstehend dasselbe wohin auch immer fortsetzen. Außerdem ist es nötig, dass in allen mehr als Sechssilbigen eine Wiederholung der Töne ist. Sodann im sechssilbigen Thema sind die Zusammenfassungen der Änderungen diese:
| I. | ut re mi fa sol la die Veränderung der Ordnung ist | 720 |
| II. | ut ut re mi fa sol,die Veränderung der Ordnung ist 720-120 macht 600. Aber nicht nur ut, sondern auch ein beliebiges der 6 Töne kann 2 mal, also 6*600 macht 3.600, und die verbliebenen 5 Töne immer 5 mal, die anderen 4 können nach u tut gesetzt werden, nämlich re, mi, fa, sol, re, mi, fa, la, re, mi, sol, la. re, fa, sol, la. mi, fa, sol, la; oder 5 Dinge haben 5 Verbindungen von 4: 5*3.600 macht | 18.000 |
| III. | ut ut re re mi fa, 480 ᴖ 15 macht 7200 ᴖ 6 macht | 43.200 |
| IV. | ut ut re re mi mi, 360 ᴖ 20 macht | 7.200 |
| V. | ut ut ut re mi fa, 360 ᴖ 6 f. 2160 ᴖ 20 macht | 43.200 |
| VI. | ut ut ut re re mi, 360 ᴖ 6 ᴖ 5 ᴖ 4 macht | 43.200 |
| VII. | ut ut ut re re re, 240 ᴖ 15 macht | 3.600 |
| VIII. | ut ut ut ut re mi, 360 ᴖ 6 ᴖ 10 macht | 21.600 |
| IX. | ut ut ut ut re re, 240 ᴖ 6 ᴖ 5 macht | 7.200 |
| Summe | 187.920 | |
Was aber wenn der 7. Ton des Erycius Puteanus, wenn Pausen, wenn solche ungleichen Geschwindigkeiten in den Noten, wenn wir andere musikalischen Symbole anwendeten auf die Berechnung, wenn zum Thema sehr viel mehr Silben als 6, wenn wir weitergingen zu Zusammengesetzten, wie groß wäre das Meer der Melodien, welche durch irgendwelche Fälle brauchbar sein könnten? Es erinnert uns an die Nachbarschaft der Dinge, kann einer beliebigen Gattung der Lieder die brauchbaren Arten oder Wendung, und gleichsam Melodien gefunden werden, die ich weiß nicht irgendjemandem so weit oder zu versuchen in den Sinn gekommen wäre. Wir wollen es mit dem Hexameter versuchen. Weil der Hexameter sechs Füße hat, unter anderen können freilich gewöhnlich der Daktylus und der Spondaeus wohnen, aber als drittvorletzten nur den Daktylus, als letzten den Spondaeus oder Trochaeus gerne hat. Was also die 4 ersten betrifft, sie sind entweder nur Daktyli: 1, oder nur Spondaei: 1, oder 3 Daktyli, ein Spondaneus, oder umgekehrt: 2, oder 2 Daktyli, 2 Spondaei: 1, überall ist die Änderung der Stellung 12, 2+1 macht 3 * 12 macht 36 + 1 + 1 macht 38. Aber in einzelnen Versen dieser Art ist der letzte entweder ein Spondaeus oder ein Trochaeus, 2* 38 macht 76. So viele Arten des Hexameters gibt es, nur durch das Versmaß der Bestandteile. Wenn ich die Änderungen verschweige, die aus den Tonhöhen kommen, z. B. was entweder aus einsilbigen oder zweisilbigen usw. oder auf diesen untereinander gemischten beruht; weil die Stimme eben mit dem Versmaß beschränkt wird, macht es sogleich einen Einschnitt und dieser ändert die Art; weil das Ausatmen häufig dazwischen tritt entweder irgendeine oder keine. Übrigens unterscheiden die Hexameter sich auch durch die Menge der Buchstaben, wie in dieser Angelegenheit das Lied des Publilius Optatianus Porfyrius herausragt (den Cesare Baronio bösartig mit Porphyrios dem Griechen, einem Philosophen und Christenfeind verwechselt) an Flavius Valerius Constantinus Magnus, das aus 26 heroischen Versen besteht, deren erster 25 Buchstaben enthält, die übrigen fortlaufend um einen Buchstaben anwachsen, bis zum 26. Der 50 hat; so stellen sie alle Register der Orgel dar. Sie haben erinnert an Sophronius Eusebius Hieronymus an Paula von Rom, Iulius Firmicus Maternus in der Mythologie, Rabanus Maurus, Beda Venerabilis über das Versmaß. Justus Velsius hat es mit Abbildungen herausgegeben aus seiner Bibliothek Augusta im Jahre 1591. Füge dazu Erycius Puteanus in "Die Wunder der Nächstenliebe" Buchst. N, der behauptet dieses Lied zurück gebracht zu haben aus der verdienten Verbannung; Gerhard Johannes Vossius in Zusammenstellung römischer Dichter siehe Optatianus; ebenso über die griechischen Historiker, 1. 16. Caspar von Barth Aufsatz über die lateinische Sprache, und August Buchner Noten in der Hymne des Venantius Honorius Clementianus Fortunatus über die Auferstehung (die gewöhnlich Lucius Caecilius Firmianus Lactantius zugeschieben wird) siehe 29. Seite 27, der die Hexameter in Form der Panflöte beachtet, der Vers nimmt durch die Mitte zu: Augusto Victoria usw. die Regeln der Orgel, die anacreontischen dimetrischen Jamben alle 18 Buchstaben entsprechen den Flötenrohren. Die Verse haben wir dargestellt, weil sie nicht allenthalben vorkommen:
| 25 | O si diviso Metiri Limite Clio |
| 26 | Una Lege Sui Uno Manantia Fonte |
| 27 | Aonio Versus Heroi Jure Manente |
| 28 | Ausuro Donet Metri Felicia Texta |
| 29 | Augeri Longo Patiens Exordia Fine |
| 30 | Exiguo Cursu Parvo Crescentia Motu |
| 31 | Ultima Postremo Donec Vestigia Tota |
| 32 | Ascensus Jugi Cumulato Limite Cludat |
| 33 | Uno Bis Spatio Versus Elementa Prioris |
| 34 | Dinumerans Cogens Aequali Lege Retenta |
| 35 | Parva Nimis Longis Et Visu Dissona Multum |
| 36 | Tempore Sub Parili Metri Rationibus Isdem |
| 37 | Dimidium Numero Musis Tamen Aequiparantem |
| 38 | Haec Erit In Varios Species Aptissima Cantus |
| 39 | Perque Modos Gradibus Surget Fecunda Sonoris |
| 40 | Aere Caro Et Tereti Calamis Crescentibus Aucta |
| 41 | Quis Bene Suppositis Quadratis Ordine Plectris |
| 42 | Artificis Manus Innumeros Clauditque Aperitque |
| 43 | Spiramenta Probans Placitis Bene Consona Rythmis |
| 44 | Sub Quibus Unda Latens Properantibus Incita Ventis |
| 45 | Quas Vicibus Crebris Iuvenum Labor Haud Sibi Discors |
| 46 | Hinc Atque Hinc Animaeque Agitant Augetque Reluctans |
| 47 | Compositum Ad Numeros Propriumque Ad Carmina Praestat |
| 48 | Quodque Queat Minimum Admotum Intremefacta Frequenter |
| 48 | Plectra Adaperta Sequi Aut Placitos Bene Claudere Cantus |
| 50 | Jamque Metro Et Rythmis Praestringere Quicquid Ubique Est. |
| 25 | Post martios labores, | 38 | Feruntque dona laeti. |
| 26 | Et Caesarum parentes | 38 | Jam Roma culmen orbis |
| 27 | Virtutibus, per orbem | 40 | Dat munera et coronas |
| 28 | Tot laureas virentes, | 41 | Auro fereos coruscas |
| 29 | Et Principis trophaea; | 42 | Victorias triumphis, |
| 30 | Felicibus triumphis | 43 | Votaque jam theatris |
| 31 | Exultat omnis aetas, | 44 | Redduntur et Choreis. |
| 32 | Urbesque flore grato | 45 | Me sors iniqua laetis |
| 33 | Et frondibus decoris | 46 | Solemnibus remotum |
| 34 | Totis virent plateis. | 47 | Vix haec sonare sivit |
| 35 | Hinc ordo veste clara | 48 | Tot vota fronte Phoebi |
| 36 | In purpuris honorum | 49 | Versuque comta sola, |
| 37 | Fausto precantur ore, | 50 | Augusta rite seclis. |
Aus denen können sie vieles über die Schriften der Alten beobachten, besonders den Diphthong Æ bei dem zwei Buchstaben als einziger ausgedrückt wird; welcher jedoch nicht der Brauch ist, weil die Überlegung siegen würde, denn was wie einer klingt muss auch ein Buchstabe sein. Aber dazu haben wir von Publilius Optatianus Porfyrius oder deswegen ausgedehnt gesprochen, dass wir voreingenommen waren nachstehend zu sprechen, wo wir uns auf die von ihm zusammengestellten die Proteus-Verse berufen werden.
Fragestellung VII.
Bei gegebenem Hauptsatz die Veränderung zu finden.
Dieses haben wir in den obigen Verknüpfungen gelöst. Nun über die Veränderungen der Reihenfolge: Es gibt verschiedene Fälle. Denn der Hauptsatz dessen Veränderung entweder aus einer Sache besteht oder aus mehreren: wenn aus einer, ist diese entweder einheitlich oder es wird das eine oder das andere unter die (zu verändernden) Dinge gegeben: die selbst einheitlich sind. Wenn es aber aus mehreren besteht, ferner aber wird es innerhalb des Hauptsatzes gegenseitig einheitlich gegeben oder nicht, ebenso sind sie äußerlich einige inwendig einheitlich oder nicht.
" Deshalb werden die äußerlichen Dinge zuerst vom festbleibenden Hauptsatz der Veränderung gezählt; und die Veränderung derer untereinander gesucht (und wenn sie unzusammenhängend wären oder der Hauptsatz zwischen sie gelegt wird) vom abgekürzten Hauptsatz, würde das Ergebnis A nach Fragestellung 4 genannt werden. Wenn der Hauptsatz nicht vielfältigungsfähig ist, oder auch nicht aus mehreren Dingen besteht, und eine dessen Dingen nicht einheitliche hätte, wird das Ergebnis A das gesuchte sein.
Wenn aber der Hauptsatz vielfältigbar ist und aus einer einheitlichen Sache besteht, werde das Ergebnis A mit der Anzahl der einheitlichen multipliziert gleich in jenen Hauptsatz einsetzbar, und das gesuchte wird gemacht sein.
Wenn aber der Hauptsatz aus mehreren Sachen besteht ist die Veränderung dieser untereinander gefragt, (und wenn sie unzusammenhängend wären oder äußerliche Dinge sind sie einzuschieben) nach Fragestellung 5 werden sie zurückgeführt auf das Ergebnis A, jedes einzelne so erstellte werden wir B nennen. Wenn schon die Sache des Hauptsatzes keine gleichartige außerhalb des Hauptsatzes hat, wird das Ergebnis B das gesuchte sein. Wenn die Sache des Hauptsatzes homogene nur außerhalb des Hauptsatzes hat, nicht innerhalb, wird das Ergebnis B mit der Anzahl der homogenen Sachen multipliziert, und wenn sie oft homogen sind, werden sie gemacht aus der Anzahl der zuerst homogenen fortlaufend multipliziert mit der nachfolgenden Anzahl der homogenen, und das Ergebnis wird das gesuchte sein.
Wenn aber das Ding des Hauptsatzes keine homogenen innerhalb und außerhalb des Hauptsatzes hat, würden zuerst die innewohnenden homogenen Dinge gezählt, und die äußerlichen ebenso, und zugrunde gelegt für die zu verbindende Anzahl; danach wird die gegebene homogene Sache nur innerhalb des Hauptsatzes für den Exponenten zugrunde gelegt. Mit gegebener Anzahl und Exponent wird die Schlussfolgerung nach Fragestellung I gesucht und wenn sie öfter Einheitlichkeit erreicht, werden die Schlussfolgerungen fortlaufend gegenseitig in sich gezogen."
Die Schlussfolgerung oder das Ergebnis aus den Schlussfolgerungen werden in das Ergebnis B gezogen. Und das gesuchte wird fertig sein. Diese Fragestellung bewirkt eine Vielzahl sehr mühsamer Fälle, und deren Lösung verursacht uns große Mühe und Zeit. Aber anders wird niemand die folgenden Fragestellungen auf den Grundlagen der Wissenschaft lösen. Aus diesen wird deshalb der Nutzen derer ersichtlich.
Fragestellung VIII.
Andere gewöhnliche Veränderungen bei gegebenem Hauptsatz zu finden.
Wird jeder der beiden Hauptsatz in dieselbe Veränderung überführt wäre es ein einziger zusammengesetzter Hauptsatz (wiewohl manchmal die Dinge des zusammengesetzten Hauptsatzes nicht zusammengesetzt wären) und wird die Veränderungen eines zusammengesetzten Hauptsatzes durch Fragestellung 10 ausfindig gemacht, wird das Ergebnis das gesuchte sein.
Fragestellung IX.
Gewöhnliche Veränderungen die Hauptsätze haben zu finden.
Wenn die meisten Hauptsätze in der Veränderung der Ordnung am derselben Stelle zusammenfallen, entweder im Ganzen oder zum Teil, haben sie keine allgemeinen Veränderungen. 2. Wenn die gleiche einheitliche Sache in den meisten Hauptsätzen auftritt, haben diese keine allgemeinen Veränderungen. Alle anderen haben allgemeine Veränderungen.
Fragestellung X.
Die Hauptsätze der brauchbaren oder unbrauchbaren Anordnunge zu finden.
Die Hauptsätze in der Welt zu finden ist dargelegt worden. Denn eine beliebige Sache an sich ist der Hauptsatz, entweder an welchem Ort auch immer für sich, oder mit was auch immer, dem einen oder anderen, gleichfalls wohin auch immer am Ort dem einen oder anderen, kurz gesagt, alle Zusammenfassung oder Anordnungen im Untersatz und derselben Sachen, oder welche gesamt in anderen enthalten sind. Aber die Verfahren in den Hauptsätzen die brauchbaren anzuordnen, damit wir von den geringeren zu den wichtigeren fortschreiten, jedes Mal wenn uns z. B. empfohlen worden ist alle Anordnungen vor Augen zu führen, was Jeremias Drexel an der erwähnten Stelle unter Bezug auf Erycius Puteanus und Gregor Kleppis und Matthäus Reimer gemacht haben.
Im Übrigen, damit die brauchbaren oder unbrauchbaren Hauptsätze gefunden werden, ist die anzuwendende Lehrmethode die der zu verändernde Sache, oder alles auf das das Zusammengesetzte sich bezieht. Deren Regeln löschen allerdings die unbrauchbaren aus, aber die brauchbaren bleiben übrig. Dann ist zu erkennen welche mit welchen und an welcher Stelle nicht verknüpft werden können, ebenso welche nicht einfach an welche Stelle gesetzt werden können, z. B. an die erste, dritte u.s.w. besonders aber an die erste und die letzte. Ferner ist zu erkennen welche Sache der wichtigste Grund der Ausnahme wäre (z. B. bei hexametrischen Versen des Proteus die kurzen Silben). Dieses ist für alles übrigen herzuleiten, ebenso für alle Orten, wenn aber jedes Mal über die meisten die entscheiden ist, wird es hinreichend sein es an einem versucht zu haben.
Fragestellung XI.
Die unbrauchbaren Anordnungen zu finden.
Es gibt zwei Vorgehensweisen "1. mit Fragestellung 12 auf diese Weise: von der gefundenen Gesamtzahl der brauchbaren und unbrauchbaren Veränderungen durch Fragestellung 4 wird die Gesamtzahl der brauchbaren nach der zweiten Methode in Fragestellung 12 abgezogen; der Rest wird das gesuchte sein.
(2.) vollständig auf diese Weise: die Hauptsätze der unbrauchbaren Veränderungen sollen mit Fragestellung 10 gefunden werden es sollen die Veränderungen der einzelnen Hauptsätze gefunden werden durch Fragestellung 7 falls welche Hauptsätze gewöhnliche Veränderungen haben nach Fragestellung 9 wird die Anzahl derer nach Fragestellung 8 gefunden und nur in einem der Hauptsätze, die die gewöhnlichen Veränderungen haben übrig gelassen würden, von den übrigen Veränderungen abgezogen wird, oder wenn man diese Arbeit des Abziehens vermeiden wollte, setze die am meisten zusammengesetzten Hauptsätze sofort an den Anfang, vergleiche Fragestellung 8. Die Zusammenfassung aller Veränderungen aus allen Schlussfolgerungen, nach Abzug der abzuziehenden, wird das gesuchte sein."
Fragestellung XII.
Die brauchbaren Anordnungen zu finden.
Die Lösung ist wie im unmittelbar vorangehenden, wenn man diese wenigstens vertauscht, auf dem Wege 1. wie in Fragestellung 12. hinterher 11. usw. und die Summe der unbrauchbaren wird abgezogen durch die 2. Methode in Fragestellung 11. Auf dem 2. Weg werden die brauchbaren Hauptsätze der Anordnungen gefunden? Die übrigen wie in der folgenden Fragestellung.
Die Anwendung der Fragestellungen 7, 8, 9, 10, 11, 12.
Wenn wem diese Fragestellungen entweder wohlfeil oder unnötig erscheinen, er wird, wenn er von seiner überheblichen Handhabung herabsteigt, etwas anderes sagen. Denn äußerst selten lässt entweder die Natur der Dinge oder der Schein es zu, dass alle möglichen Anordnungen brauchbar sind. Welches Beispiel in der Veranschaulichung vielleicht weniger nützlich ist, doch sind wir im zu gebenden Beispiel höchst anschaulich.
Wir haben oben gesagt, die Proteus-Verse sind reine Proteus´sche, das ist in denen die meisten möglichen Anordnungen brauchbar sind, diese allerdings bestehen beinahe völlig aus einsilbigen; oder aus gemischten, in denen die meisten unter die unbrauchbaren fallen, so wie die mehrsilbig sind und diejenige schließt die kurzen ein.
Bei dieser Gattung wäre mir unter den Alten Publilius Optatianus Porfyrius aufgefallen, der solches gewisses versucht hat, ebenso jenes von den in der Fragestellung VI. Und Erycius Puteanus überliefert in "Wunder der Frömmigkeit", Buchstabe N Seite 92 unter anderem diese aus den Versen des Flavius Valerius Constantinus Magnus:
- Wen der göttliche Kaiser Constantin hervorgebracht hat,
- Ist geboren das goldene Zeitalter Roms fortzuführen.
Der erste von denen ist der Torpalius oder der Symphalicus bestehend aus mit der Silbe fortlaufend ansteigenden Betonung; ein anderer ist der sechsfüßige Proteus, wenn es erlaubt ist ihn so zu nennen.
- Aurea Romanis propagans secula nato
- Aurea propagans Romanis secula nato
- Secula Romanis propagans aurea nato
- Secula propagans Romanis aurea nato
- Propagans Romanis aurea secula nato
- Romanis propagans aurea secula nato.
Wirklich viele hat als Erster jener Marcus Pedo Vergilianus:
- Du Tityre ruhst zurückgelehnt unter dem Blätterdach der Buche.
der die Anwendung beinahe zum Scherz wendet. Dessen Anordnungen sind diese: für "Dich unter" 2. für "weit zurückgelehnt" 2 und "Tityre" bald am Anfang, wie jetzt, bald "Blätterdach" am Anfang: bald "Tityre [unter dem] Blätterdach" am Ende, bald "Blätterdach Tityre" am Ende 4 · 2 · 2 macht 16. Aber in den Gedichten des Porphyrios ist nicht der einzelne Proteus-Verse, sondern alle, und nicht ein Vers, sondern das gesamte Lied ist so sehr bewundernswert. Diese Art Verse zusammenzustellen ist eine zu vollbringende Aufgabe, dass die passenden Betonungen entweder beginnen oder beenden.
Ein anderer der auch den Namen Proteus bekannt macht, ist Julius Caesar Scaliger ein Mann wenn die Wildheit des Scharfsinns fehlte, vollkommen unvergleichlich, "Die Dichter" 2. Buch, Kapitel 30, Seite 185, dieser hat die unzähligen, wie er selbst sagt, Formen zusammengestellt, wie unsere 64.
- Listig hast du gehofft, die Götter werden dich übersehen, Proteus.
Er wird vieles nicht leicht finden, wer dessen Spuren unserer Berechnungen liest. Für "listig übersehen" 2, für "Proteus die Götter" 2 · 2 macht 4, "Du hast gehofft die Götter dich" hat 6 · 4 macht 24 Anordnungen, "die Götter listig die gehofft" hat 2 Anordnungen, "Divos Te sperasti perfide" hat 6 + 2 + 2 macht 10 · 4 macht 40 + 24 macht 64. Wir haben ebenso bei Publius Vergilius Maro, allerdings sogar mehr Anordnungen beobachtet, Aeneis, 1. Buch, Vers 282. Diese setze ich weder als Spitze der Dinge noch der Zeiten. Denn "perfide" ist eine Betonung, "queis ego" kann in zwei geteilt werden.
Ich komme zu jenem scharfsinnigen Bernardus Bauhusius, einem Jesuiten aus Leuven, der unter den Sinngedichten hervorsticht, wie zum Beispiel oben in der Fragestellung 4, über Christus, so ist es hier über Maria:
- So viele sind Dir die Gaben Jungfrau, wie Sterne am Himmel.
Würdig ist diese bemerkenswerte Arbeit, die der sehr gebildete Herr Erycius Puteanus ausgeführt hat in einem Büchlein, das er "Wunder der Frömmigkeit" betitelt hat, herausgegeben im Quartformat in Antwerpen im Jahre 1617, und dessen brauchbare Anordnungen er alle abzählt von Seite 3 bis Seite 50, eingeschlossen welche vom Autor, wenn sie auch innerhalb der Schranken weiter ausgedehnt wurden, er hat die Anzahl 1022 erhalten, weil die Astronomen gewöhnlich ebenso viele Sterne zählen, aber er sich selbst vorgenommen hat zu zeigen, dass es nicht weniger Gaben als Sterne gibt; ferner weil er es mit nahezu sehr großer Sorgfalt vermieden hat zu sagen, alle jene die gesehen werden, dass es so viele Sterne am Himmel gibt, wie Maria Gaben hat, denn die Gaben Marias sind sehr viel mehr. Deshalb hätte er diese Anordnungern (z. B. "Quot tibi sunt dotes virgo, tot sidera coelo") als ebenso viele angenommen, nämlich 1022. So viele andere Verse wie nötig einzufügen und andererseits, dass sie zum Vorschein kommen werden ist offensichtlich. Dies merkt aber Erycius Puteanus auch im Vorwort auf Seite 12 an, manchmal verstehen wir nicht so viele Sterne, sondern auch Gaben hängen am Himmel, wie es Himmelskörper gibt, z. B.
- So viele Gaben sind Dir im Himmel, wie Sterne Jungfrau.
Darüber hinaus macht er im Bezug auf Anordnungen vieles, was sie bei "Virgo" und "Dir" der gewissermaßen zweifelhaften Zählung, und zusammengerafft und hervorgebracht zu werden zulassen, welchen Kunstgriff wir auch vereinzelt bei Christian Daum beobachtet haben.
Dies merkt aber Erycius Puteanus auch im Vorwort auf Seite 12 an, manchmal verstehen wir nicht so viele Sterne, sondern auch Gaben hängen am Himmel, wie es Himmelskörper gibt, z. B.
Darüber hinaus macht er im Bezug auf Veränderungen vieles, was sie bei Virgo und Dir zweifelhaft gewissermaßen gezählt und auseinandergerissen und hervorgebracht zulassen, welchen Kunstgriff wir auch vereinzelt bei Christian Daum beobachtet haben. Erycius Puteanus hat ferner mehrmals an das Wunder und seiner Proteus-Verse des Bernardus Bauhusius in der Zusammenstellung der Briefe cent. I Briefe 49 und 57 an Gisbert Bauhusius, den Vater des Bernardus Bauhusius, füge die Briefe 51, 52, 53, 56 ebenda. Ich habe eine Ausgabe dieser Briefe erschienen 1647 in Amsterdam im Duodez Format, denn in der Ausgabe im Quartformat die er schon 1612 herausgegeben hat, habe ich vergeblich gesucht.
Außerdem hat Giovanni Battista Riccioli im Almagestum verus & novum Teil I, Buch 6 Kap. 6, Fußnote 1 durch den Fehler des erinnerten Verses des Bernardus Bauhusius den Autor Erycius Puteanus dieser Worte erklärt: weil es ja aber alt war die bis heute fortgeführte Meinung von Claudius Ptolemäus, dass 1022 die Zahl aller Sterne ist. Erycius Puteanus hat den Nachfolgern ein Denkmal seiner Frömmigkeit und seines Scharfsinnes hinterlassen in jenem höchst kunstvollen Lied "Tot Tibi etc." der jedoch nicht Autor sondern Erfasser und Förderer ist.
Endlich haben wir beobachtet, dass er geradewegs den ähnlichen Vers in Publius Ovidius Naso mit geringsten Veränderungen diesen aus Metamorphoses XII, Fabel 7 siehe S. 594 hat.
- Det mihi se, faxo triplici quid cuspide possim
- Sentiat &c.
Das wird folgendes:
- Dant mihi se faxo trina quid cuspide possim.
Denn auch die letzte ist bezüglich " mihi et faxo" zweideutig. Auf diesem Gebiet ragt Gregor Kleppis heraus, des heimischen gefeierten Dichters, ein Vers ist hier:
- Dresden sind nun drei gegeben, gleich wie die Sonne gibt, Zierden das Licht.
dessen Veränderungen er in einem besonderen Büchlein bis 1617 gezählt hat; die Gelegenheit es den drei Sonnen zu widmen, welche im Jahre 1617 am Himmel strahlten, zu welcher Zeit die drei irdischen Sonnen in Dresden zusammen kamen waren in Österreich zuhause: der Kaiser Matthias, Ferdinand II, König von Böhmen und Erzherzog Maximilian von Österreich, der Oberste Meister des Deutschherren Ordens. Das Büchlein das jenen gewidmet ist mit dem Titel "Proteus Gedichte" hat er im selben Jahr herausgegeben, was die Anzahl der Veränderungen anzeigt.
Aber insgesamt gibt es mehr Veränderungen als 1617, was selbst der Autor stillschweigend bekennt, wenn auch nur am Ende zwischen den Druckfehlern verteidigt er sich so: es könnte vorgekommen sein, dass er in einer so großen Menge irgendeines zweimal gesetzt hätte, er hätte sie deswegen eingefügt, um einige neue Lücken aufzufüllen, welche er sicher sei noch nicht gehabt zu haben. Dass wir irgendein Verfahren für die naheliegendsten Fragestellungen aufzeigten, wir werden alle brauchbaren Veränderungen berechnen. Das wird so gemacht, wenn wir alle unbrauchbaren finden werden. Die Hauptsätz der Veränderungen haben wir durch Noten der Länge ausgedrückt, denn so hätten wir für mehrere Umstellungen eine angenommen , z. B. — — . — . — . ◡ ◡ . sie enthält auch diese — . — — . — . ◡ ◡ u.s.w. Mit Punkten bezeichnen wir eine Betonung und schließen sie ein.
| Die Summe aller brauchbaren und unbrauchbaren Veränderungen: | 362.880 | |
| 1. | ◡ ◡ . v.g. dant jam Dresdae ceu sol dat lumina lucem | 40.320 |
| 2. | — — . ◡ ◡ . Dresdae tria dant jam ceu sol etc. | 10.080 |
| 3. | — . — . ◡◡ . dant jam tria. | 14.400 |
| 4. | — — . — . — . ◡◡ . Dresdae dant jam tria. | 28.800 |
| 5. | — — . — — . ◡◡ . Dresdae lucem tria. | 1.440 |
| 6. | — . — . — . — . ◡◡ . dant jam ceu sol tria. | 2.880 |
| 7. | — — . — — . — . — . ◡◡ . Dresdae lucem ceu sol tria. | 28.800 |
| 8. | — — . — . — . — . — . —◡ . Dresdae dant jam ceu sol tria. | 7.200 |
| 9. | — — . — — . — . — . — . ◡◡ . Dresdae lucem dant jam ceu sol tria. | 7.200 |
| 10. | am Ende ◡◡ . v. g. tria | 40.320 |
| Summe der unbrauchbaren Veränderungen wegen der Betonung von Tria, die genau die Hälfte der brauchbaren Veränderungen beträgt. |
181.440 | |
| 11. | am Anfang: — . —◡◡ . dant lumina. | 18.000 |
| 12. | — . — — . —◡◡ . dant Dresdae lumina. | 9.600 |
| 13. | — . — . — . —◡◡ . dant jam ceu lumina. | 4.320 |
| 14. | — . — . — . — . — . —◡◡ . dant jam ceu dat lumina. | 240 |
| 15. | — . — — . — — . —◡◡ . dant Dresdae lucem lumina. | 2.160 |
| 16. | — . — . — . — — . —◡◡ . dant jam ceu lucem lumina. | 5.760 |
| 17. | — . — . — . — . — . — — . —◡◡ . dant ceu jam sol dat lucem lumina. | 0 |
| 18. | — . — . — . — — . — — . —◡◡ . dant ceu jam Dresdae lucem lumina. | 1200 |
| 19. | — . — . — . — . — . — — . — — . ◡◡ . dant ceu jam sol dat lucem Dresdae lumina. | 0 |
| 20. | am Ende —◡◡ . v. g. lumina | 11.620 |
| Summe der unbrauchbaren Veränderungen wegen Betonung Lumina | 52.900 | |
| 21. | ੜberall: —◡◡ . ◡◡ . lumina tria | 40.320 |
| 22. | —◡◡ . —◡◡ . lumina Dresdae tria | 14.440 |
| 23. | —◡◡ . — . — . —◡◡ . lumina ceu jam tria | 4.800 |
| 24. | —◡◡ . — . — . — . — . ◡◡ . lumina ceu jam sol dat tria | 1.440 |
| 25. | —◡◡ . — — . — — . ◡◡ . lumina Dresdae lucem tria | 480 |
| 26. | —◡◡ . — . — . — — . ◡◡ . lumina ceu jam Dresdae tria | 4.800 |
| 27. | —◡◡ . — . — . — — . — — . ◡◡ . lumina ceu jam Dresdae lucem tria | 4.080 |
| 28. | —◡◡ . — . — . — . — . — — . ◡◡ . lumina ceu jam dat sol lucem Dresdae tria | 532 |
| 29. | —◡◡ . — . — . — . — . — — . ◡◡ . lumina ceu jam dat sol lucem Dresdae tria | 2.978 |
| Summe der unbrauchbaren Veränderungen wegen Vervielfältigung Lumina und Tria, durch Voranstellen. |
59.870 | |
| 30. | — . ◡◡ . — . — . ◡◡ . dant tria jam lumina. | 2.400 |
| 31. | — . ◡◡ . — . — — . — . ◡◡ . dant tria jam Dresdae lumina. | 3.840 |
| 32. | — . ◡◡ . — . — . — . —◡◡ . ceu sol | 1.440 |
| 33. | — . ◡◡ . — . — . — . — — . —◡◡ . dant tria jam ceu sol lucem lumina. | 5.760 |
| 34. | — . ◡◡ . — . — . — . — — . — — . —◡◡ . dant tria jam ceu sol lucem Dresdae lumina | 9.360 |
| Summe der unbrauchbaren Veränderungen wegen Vervielfältigung Tria und Lumina, jene vorangestllt | 22.800 59870 52.900 181.440 |
|
| Gesamtsumme der unbrauchbaren Veränderungen | 317.010 | |
| nach Abzug von der Gesamtsumme | 362.880 | |
| verbleibt | ||
| Summe brauchbarer Veränderungen gemäß Kleppisius der Spondeen zuläßt | 45.870 | |
| Die Spondeen haben wir ausgelassen um den Aufwand der Berechnung nicht zu vergrößern, denn wie viele brauchbaren und unbrauchbaren Veränderungen entstehen aus dem Spondeus, finde ich so: | ||
| 1. | wenn ans Ende gesetzt — . — — . v.g. dant lucem | 100.800 |
| 2. | — — . — — . v. g. Dresdae lucem | 10.080 |
| 3. | — . — . — . v. g. dant seu sol | 43.300 |
| Summe aller brauchbaren und unbrauchbaren der Spondeen | 154.080 | |
Darüber hinaus ragt der Heldenvers des sehr berühmten Carl von Goldstein heraus:
- Die Kunst ist nicht derartige gut aufgebaute Verse zu schreiben,
In der Kunst sich zu verleugnen ist der kunstfertig, welcher 1644 Veränderungen zu enthalten genannt wird. Im Wettstreit derer, besonders mit Gregor Kleppis, ist Henricus Reimerus aus Lüneburg an der örtlichen Schule am Johannis Kolleg der über Proteus unterrichtet, derartiges hervorgegangen:
- Gib gnädiger Christ der Stadt heiteren Frieden in unserer Zeit.
die er fortsetzt im gleichen Jahr 1619, in dem alle dessen Veränderungen in einem Büchlein im Duodez Format eingeschlossen in Hamburg erschienen hervorgegangen sind.
Auch der in aller Art von Gedichten sehr fleißige Christian Daum, ein , hat freilich deswegen nicht gewollt, dass ihm entgegengehalten wird, er sei zurückgeblieben. Ich würde nichts über dessen Fülle sagen, über welche Lieder derselbe er dreitausendfach gesprochen hat (denn hier müssen nicht andere Worte, sondern es muss eine andere Anordnung derselben Worte sein) was er über diesem Satz: es werde Gerechtigkeit oder die Welt geht unter, vom den Dichter Vertumnus in Zwickau im Jahr 1646 im Oktav herausgegeben, vorangestellt hat. Ich wende mich wenigstens dem zu, was auch vom Autor in der Klosterhandschrift 1 Zeilen 219 und 220 als Proteus Verse bemerkt wurde. Diese sind die folgenden:
- v. 219: Entweder Macht, Betrug und Recht fehlen, oder der Himmel stürzt ein.
- v. 220: Macht, Betrug, Streit fehlen, Gleichheit tragen, oder der Erdkreis stürzt ein.
Aber neulich haben wir gefunden, von ihm selbst mitgeteilt, ich würdige einen seiner anderen Verse, den er gefunden hat, ohne ihn zu veröffentlichen, der es verdient mehr als Proteus genannt zu werden, denn nicht so sehr in demselben, sondern er wird in viele andere Arten Lieder umgewandelt. Denn die Worte sind diese: Oh Gütiger (d. h. Gott) Verherrlichter Petrus (Jünger) es wäre ein doppelter Gewinn: die mannigfaltigen Umstellungen ergeben 8 Alcaicos, 8 Phaleucios, 14 Sapphicos, 42 Archilochios, in denen allen das Weglassen unbetonter Silben vorliegt. Aber fürwahr ohne Elision [Auslassen von Silben] macht er 32 Pentameter, sechsfüßige Jamben nur 20, Scazontes nur 22, Scazontes und Jamben zugleich 44 (und so alle Jamben 64 alle Scazontes 66) wenn man eine Silbe zufügt wäre es ein Hexameter, z. B.
- Fac duplo Petrus lucro sit mactus, o alme!
veränderlich zu 480 Versen.
Übrigens der größte Teil der Kunstfertigkeit besteht darin, dass die meisten Silben, wie die erste im Doppel, Petrus, Reichtum, zweideutig sind. Aber die Elision [Auslassen von Silben] wirkt wie ebendieselben Worte, durch das Weglassen von Silben ergeben sich verschiedene Arten des Lieds. Einen anderen hatte er schon im Jahre 1655 gegeben, aber weniger der Veränderungen, nämlich diesen alkäischen Vers:
- Faustum alma sponsis da Trias o torum!
Umwandelbar in 4 Phaleucios, 5 Sapphicos, 8 Pentameter, 8 Archilochius, 14 sechsfüßige Jamben, 14 Scazonten.
- Sed jam tempus equum spumantia solvere colla.
Wenn dennoch jemand unsere Weitschweifigkeit missbilligt, achte ich das; damit es nicht zur Gewohnheit gekommen sein wird, gegen die Kürze wendet sich das Glück.
zurück zum Anfang des Kapitels
Ende
Quellen:
- Gottfredo Guilielmo Leibnüzio: Dissertatio de Arte Combinatoria. Lispsiae 1666.
- Gottfredo Guilielmo Leibnüzio Lisiensi: Dissertatio de Arte Combinatoria. in: Carl Immanuel Gerhardt: Leibnizens mathematische Schriften. Halle 1858. (diese Quelle enthählt nicht die Danksagung an Martin Geier!)
© Rainer Stumpe, URL: www.rainerstumpe.de/
Datenschutzerklärung