Rohfassung der Übersetzung der Monadologia Physica von Immanuel Kant

Vorbemerkungen

Die klugen Forscher, die sich dem Erforschen der Naturgeschichte widmen, haben sich zwar in einhelliger Übereinstimmung zusammengefunden, sorgfältig darauf zu achten, daß keine unbegründete Vermutung mit der ungebührlichen Erlaubnis sich gewissermaßen in die Naturwissenschaft einschleicht, noch daß etwas ohne Bewertung der Erfahrung und ohne geometrische Deutung im Einzelfalle untersucht wird. Durch diese Empfehlung konnte nichts vorteilhafteres und nützlicheres für die Wissenschaft ersonnen werden. Aber weil es kaum irgendeinem Sterblichen dauerhaft erlaubt ist, sich der Wahrheit zielstrebig in gerader Linie zu nähern, ohne von der Wahrheit hier und da ein Stück abzuweichen, waren gewisse [Forscher] diesem Grundsatz gegenüber sogar dauernd nachlässig und sie haben nur was sie unmittelbar als Ergebnis der Versuche erfahren haben, zugelassen, denn sie haben gewagt, sich der Erforschung der reinen Wahrheit mit geringstem Aufwand zu widmen und immer nach Hinweisen Ausschau gehalten. Damit können wir allerdings die Gesetze der Natur zu erklären methodisch vorankommen, die Grundlage der Gesetze und die Hintergründe können wir nicht [erklären]. Doch in wie viele [Einzelfragen] die Erscheinungen der Natur zerlegt werden, von der verborgenen Nachricht der zugrundeliegenden Ursachen sind sie immer ebenso weit entfernt, wie die, die sich selbst überredeten auf höhere und höhere Berggipfel zu steigen bis der Himmel mit Händen greifbar wäre, ebenso wenig werden sie jemals die Kenntnis der [materiellen] Körper der Natur selbst erreichen.

Deshalb ist hierbei allein die Metaphysik, von der die meisten glauben, man kann bei den Fragestellungen der Physik getrost auf sie verzichten, ein Hilfsmittel und entzündet das Licht [der Erkenntnis]. Die [faßbare] Materie [corpora] bestehen bekanntlich aus Teilen; auf welche Weise die zusammengefügt sind, ob sie nur durch die gleichzeitige Anwesenheit einfacher Teilchen, oder im wechselseitigen Streit der Kräfte den Raum erfüllen, interessiert zunächst nicht, denn es wird einleuchtend dargestellt. Aber unter welcher Bedingung ist es endlich möglich, daß in dieser Ausführung die Metaphysik mit der Geometrie verbinden, da es, wie es anerkannt wird, leichter ist, die [mythischen] Greifvögel mit den Pferden, als die Transzendentalphilosophie mit der Geometrie zu verbinden? Denn indem sie [die Philosophie] den ins unendliche teilbaren Raum beharrlich ablehnt, ebendasselbe, was im Übrigen geläufig ist, hatte sie [die Geometrie] mit Überzeugung behauptet. Diese verlangt den leeren Raum als notwendig zur freien Bewegung, jene verwirft ihn. Diese bezeichnet die Anziehung — oder allgemeine Gravitation — als von den mechanischen Ursachen kaum erklärbare, aber als innewohnende [Eigenschaft] der materiellen Körper in Ruhelage und als in die Ferne wirkende Kraft, die von ihnen ausgeht, jene verwirft das als Blendwerke eitler Einbildung.

Wenn es auch erscheint, dies zu vereinbaren sei keine geringe Arbeit, habe ich es doch unternommen einige Mühe dahinein zu stecken; anderen, deren Fähigkeiten besser hinreichen zur Aufgabe, sind ausgefordert, das zu vollenden, was ich hier zu behandeln mich bemühen werde.

Zum Abschluß füge ich das hinzu: Weil es der Ursprung aller inneren Wirkungen ist, ist also eine den Elementen innewohnende Bewegungskraft notwendig, die zwar von außen angewandt, weil jene außerhalb anwesend ist, weder können wir uns eine andere zur Bewegung anwesende Kraft vorstellen, außer einer, die sowohl abstoßen als auch anziehen kann, noch könnte ferner allein durch die Anwendung einer abstoßenden Kraft die Verbindung der Elemente zu zusammengesetzten Körpern, aber vielmehr die Zerstreuung, aber durch eine einzig anziehende [Kraft] kann nicht wirklich die bestimmte Ausdehnung im Raum verstanden werden, im Vorhergehenden ["De Igne"] kann es auf gewisse Weise verstanden werden, wodurch diese beiden Grundlagen aus der Natur der Elemente und durch die Beziehungen der einfachen [Elemente] herleiten kann, diese Ausarbeitung hat zusammengetragen, was ferner zur Erklärung der Natur der Körper nicht zu vernachlässigen ist.

Die Physik der grundlegenden Substanzen (Monaden)

Teil I.

Beweis der Vereinbarkeit der Geometrie mit der Existenz physikalischer Monaden.

Satz I.

Begriffsbestimmung.

Die einfache Substanz, Monas^*) genannt, ist, was nicht aus mehreren Teilen besteht, welche eines ohne andere allein vorkommen kann.

*) Weil es ja der Grundsatz meines Vorhabens ist, es nur der Klasse der einfachen Substanzen zu widmen, die Teile der einfachen materiellen Körper sind, erinnere ich daran, daß im Folgenden die Begriffe für die einfachen Substanzen, der Urstoffe der Materie: die Monaden, der Stammbestandteile der materiellen Körper gleichbedeutend gebraucht werden.

Satz II.

Theorem. Die materiellen Körper bestehen aus Monaden.

Weil aber die Anordnung solcher Teile nur eine Beziehung ist, daher die Abgrenzung die gegenseitige Berührung ist, die unter Erhalt ihrer [der Teile] Existenz aufgehoben werden kann, ist es offensichtlich, daß alle Zusammensetzung der Körper aufgehoben werden kann, dennoch von allen übrigen gebliebenen Teilen, die vorher zusammengesetzt waren, aber von aller aufgehobenen Zusammensetzung, sind die Teile übrig, die durchaus keine Zusammensetzung haben, und die sogar vollkomen von der Vielfalt der Substanzen verlassen wurden, daher sind sie einfache [Substanzen]. Also besteht jeder Körper aus einfachen, vollkommen unzusammengesetzten Teilen, das ist aus Monaden.

Erklärung. Absichtlich habe ich in der vorliegenden Darstellung jene allbekannte Grundlage der wissenschaftlichen Lehre [von der Zusammensetzung der Materie] auslassend, die in der Gemeinschaft der Wissenschaftler eingeführt [ist, und] welcher jedermann zustimmen wird, durch Vereinigung der Vorstellungen zusammengetragen, wenig befürchtend, daß jene, denen diese Zusammensetzung der Materie unbekannt ist, von solcher Überlegung nicht überzeugt würden.

Satz III.

Theorem. Der Raum, den die materiellen Körper erfüllen, ist unendlich teilbar, und deshalb besteht er nicht aus einfachen und nicht-zusammengesetzten Teilen.

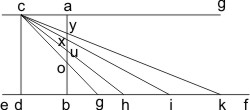Eine gegebene Linie e f unbestimmter Länge, das ist so, daß sie willkürlich immer weiter ausgedehnt werden kann, eine andere physikalische a b, das ist wenn es so beliebt, wird aus einfachen Teilen der Materie zusammengesetzt im rechten Winkel errichtet. Seitlich davon sei eine andere c d, zur vorigen parallele errichtet, man wird nicht in Abrede stellen, daß diese nicht nur in der geometrischen Bedeutung, sondern auch in der physikalischen, verstanden werden kann. Es werden auf der Linie e f beliebige Punkte g, h, i, k, und so weiter bis ins Unendliche, eingezeichnet werden. Zunächst wird niemand daran Zweifel äußern, daß man zwischen zwei beliebigen Punkten, oder wenn man lieber will gegebenen Monaden eine gerade physikalische Linie ziehen kann. Es sei [eine Linie] c g gezogen, und der Ort, an dem sie das Lot a b schneidet, sei o. Nun würde eine andere gezogene physikalische Linie zwischen den Punkten c und h gezogen, und es sei der Schnittpunkt u, der beiden Linien c h und a b gemeinsam ist, näher am Punkt a. Und so weiter, von der aus demselben Punkt c zu irgendeiner in der unendlich verlängerten Linie e f den Punkten i, k etc. gezogenen, werden immer die Schnittpunkte x, y etc. näher am Punkt a sein, wie sogar dem der Geometrie Unkundigen von selbst einleuchtet. Und wenn diese gezogenen physikalischen Linien endlich so eng zusammengepreßt sein werden daß sie einander gerade berühren, und daß zwischen ihnen keine weiteren vorkommen können, können die darunter gezogenen entfernt werden. Und trotzdem ist offensichtlich, die Orte des Schnittpunkts müssen sich dem Punkt a mehr und mehr annähern^*), jenachdem wie weiter und weiter entfernt in der unbestimmten Linie e f man den Punkt einzeichnet. Weil diese Länge allerdings ins Unendliche wachsen kann, kann die Annäherung des Schnittpunktes gegenden Punkt a auch mit unendlichen Teilen wachsen. Aber niemals fällt der Schnittpunkt unter dieser Bedingung auf den Punkt a; allerdings haben die Punkte c und a gleiche Entfernungen von der Linie e f, die Linie, die die Punkte c und a verbindet und so weit es beliebt verlängert [wurde], wird immer ebensoweit von der Grundlinie e f entfernt sein, und kann dieser niemals begegnen, weil es gegen die Grundannahme [ist, daß die Linien parallel sind]. Und solange durch die fortschreitende Teilung der Linie o a noch nicht bei den einfachen, nicht weiter teilbaren Teilen angekommen sein wird, das ist, der Raum ist unendlich teilbar, und besteht nicht aus zusammengesetzten Teilen.

*) Und niemals können die Punkte y und x zusammenfallen, weil sonst die Linien c y und c x ebenfalls zusammenfallen, und die Linie c k mit der Linie c i zusammen zusammen fallen würde, was gegen die Forderung [verstößt].

Kurze Erklärung. In dieser Darstellung habe ich hierzu geltend gemacht,was von einer großen Anzahl Naturforscher bereits benutzt wird, und es soweit dargelegt, daß größte Klarheit über den physikalischen Raum entsteht, damit nicht die Ausnahme dessen entgeht, was allgemein zur Unterscheidung der geometrischen und natürlichen Räume gebraucht wird. Es sind zwar auch andere Darstellungen dieser Meinung zur Hand, derer ich als einzige geltend machen würde, man stelle sich wenn man möchte, ein gleichseitiges Dreieck aus Monaden vor, welches wenn zwei Seiten unendlich verlängert werden, und man auf diesen Seiten des Dreiecks doppelt, dreifach, fünffach, hundertfach längere der gegebenen Strecken [abträgt], kann man die Endpunkte dieser Linien verbinden, die im gleichen Verhältnis zur dritten Seite des Dreiecks stehen werden, wie jene, ebenso großem einfachen mehrfachen [Verhältnis]. Weil aber zwischen beliebigen dieser Monaden, und zwar diese, die im Scheitel des Winkels liegt, physikalische Linien vorgestellt werden können, diese die Basis des gegebenen Dreiecks unendlich teilen, und so weit besonders die unendliche Teilbarkeit des Raumes zeigen werden. Aber wer die oben vorgetragene Darstellung ohne Behinderung durch Vorurteile angesehen haben wird, kann gewiß für alle anderen [Argumente] meiner Meinung offen sein.

Satz IV.

Theorem. Das Zusammengesetzte, das unendlich oft teilbar ist besteht nicht aus elementaren oder nicht-zusammengesetzten Teilen.

Weil im Zusammengesetzten, das unendlich teilbar ist, es niemals durch Teilen erreicht wird aus der Zusammensetzung alle Teile herauszunehmen, eine Zusammensetzung aber, die nicht durch Teilung aufgehoben werden kann, kann gerade nicht aufgehoben werden außer man spricht der Zusammenstellung alle Existenz ab; weil in der Tat, die Teile, die nach Aufheben aller Zusammensetzung in dem Zusammengesetzten verbleiben, den Einfachen des Satzes I gehorchen; es ist offensichtlich, daß unendlich teilbaren Zusammengesetzen nicht aus solchen bestehen.

Kurze Erklärung. Ich habe nichts gesagt, was der Lehre des Grundsatzes entgegenstehen wird, wonach beliebige einfache nicht-zusammengesetzte Teile aus dem Körper freigesetzt wurden, und nach der Feststellung der unendlichen Teilbarkeit ihres Raumes, sollte man sich hüten, daß man nicht irgend einer die Monaden für unendlich kleine Teilchen der Körper hielte. Denn der Raum, der eine Erscheinung ist, die vollkommen frei ist von Körperlichkeit und äußerer Beziehung der vereinigten Monaden, aber durchaus durch unendlich fortgesetzte Teilung nicht erschöpft wird, erfüllt vollauf diese Bedingung; aber es ist nur Accidens (Zufall) aus welcher möglichen Zusammensetzung die Verbindung ist, und sie sind wesentlich Bestandteile der substanziellen Verbindung, das genannte Zulassen der unendlichen Teilung ist unpassend. Denn daraus würde auch folgen, daß ein beliebiger einfacher verbundener Teil des Körpers so ist, als ob auch nicht Tausende andere, noch Myriaden, noch Millionen Millionen, mit einem Wort so viele man wird zuweisen wollen, das beliebige Teilchen der Materie zusammengesetzt bilden würde, das gewiß nicht geheimnisvoll die gesamte Körperlichkeit der Zusammengestellten beseitigt, und so nicht auf die Körper der Natur zutreffen kann.

Folgerung. Der Körper besteht demnach, wie er auch definiert wird, aus eine Anzahl einfacher Elemente.

Satz V.

Theorem. Jeder beliebiege einfache Baustein der Körper, oder die Monade, ist nicht nur im Raum [anwesend], sondern erfüllt auch den Raum, trotz seiner Einfachheit.

Weil der beliebige Körper bestimmt ist aus der Anzahl einfacher Elemente die ihn erfüllen, der Raum allerdings, den er erfüllt, würde der unendlichen Teilung unterliegen, besetzt ein beliebiges dieser Elemente einen Teil des Raums, der immer noch weiter teilbar ist, das heißt, es wird einen zuweisbaren Raum erfüllen.

Weil aber die Teilung des Raumes keine Trennung derjenigen ist, deren eines von anderen abgesondert ein eigenes selbst erhaltendes Dasein hat, sondern bloß die Vielfalt oder gewissermaßen die Menge in der äußeren Beziehung zeigen würde, wird daher offensichtlich nicht die Vielfalt der körperlichen Teile folgen; die sich einzig wegen der körperlichen Einfachheit der Monade widersetzen werden, ist es offensichtlich, daß die Teilbarkeit des Raumes nicht hinreichend der Einfachheit der Monade widerspricht.

Kurze Erklärung. Gewiß hat kein anderer Gedanke bei der Untersuchung der Elemente durch Vereinigung der Geometrie mit der Metaphysik mehr behindert, wie jene vorgefaßte, wenn auch ungenügend geprüfte Meinung, ob die Teilbarkeit des Raumes, den das Element besetzt, die Teilung der Elemente in körperliche Teile selbst zeigen würde. Was ohne Risiko des Zweifels vielmehr dauernd allgemein behauptet worden ist, daß, wer die unendliche Teilung des realen [durch Anwesenheit von Körpern definierten] Raumes behauptet, auch vor den Monaden in aller Welt zurückschaudert würde, und wer die Monaden anerkennt, hielte die Beschaffenheit des geometrischen Raumes für Einbildung, sie würden deren eigene Teile geglaubt haben. Aber weil es offenbar aus dem vorher vorgestellten einleuchtet, irrt weder die geometrischen Ansicht, noch zieht sich die beim Metaphysischen zurück, daß die Meinung vom Wahren abweicht, diese, die die beiden Meinungen trennt, als ob das Element hinsichtlcih der völlig einfachen Substanz den Raum durch seine Einfachheit nicht erfüllen könnte, und daß es notwendig ist, sie zu Fall zu bringen. Denn die Linie oder Oberfläche, die den gewissen Abstand in zwei Teile teilt, zeigt an daß ein Teil des Raumes jedenfalls außerhalb eines anderen besteht. Aber welcher Raum nicht eine Substanz ist, sondern er ist ein gewisses Phänomen des Verhältnisses äußerer Substanzen, des einen und desselben dessen Verhältnis der Substanz zweigeteilt werden kann, es würde sich durch Einfachheit sogar durch geringeren Gebruach der Substanz nicht widersetzen. Denn welches vom Teil auf beiden Seiten der teilenden Linie ist, ist nicht irgendetwas von der Substanz so abtrennbares, daß es von sich selbst abgetrennt noch eine eigene Existenz bewahren würde, was zur substanziellen Teilung, die die Einfachheit aufhebt, jedenfalls dringend erforderlich ist, aber die ausgeübte Wirkung ist einer und der selben Substanz oder Beziehung, in der man zwar eine andere Vielzahl antrifft die keine Trennung der Substanz selbst in Teile ist.

Satz VI.

Theorem. Die Monade bestimmt das Raumsegment, in dem sie anwesend ist, nicht durch die Vielzahl ihrer Teile, sondern durch ihren Wirkkreis, der die auf beiden Seiten von ihr äußerlich Anwesenden abhält von gegenseitiger Annäherung der ihr entfernteren.

Weil in der Monade keine Vielfalt der Substanzen vorhanden ist, indessen erfüllt sie jedoch allein durch ihre Lage den Raum, mit der vorangegangenen Überlegeung zum erfüllten Raum wird nicht nur in der Lage der Substanz, sondern unter Berücksichtigung der Beziehung ihrer äußerlichen zu suchen sein. Weil aber der zu erfüllende Raum die auf beiden Seiten unmittelbar Anwesenden sich von der gegenseitigen Annäherung der Erntfernteren abhält, und so weit es durch die Lage ihrer selbst irgendetwas begrenzt, nämlich das Maß der Nähe, zu der sie selbst sich annähern können, zur Begrenzung, ist es offensichtlich, daß sie eine Wirkung entfalten und zwar im Raume in alle Richtungen begrenzt, und daher ist zuzugestehen, daß sie diesen Raum durch ihren Wirkkreis erfüllen.

Satz VII.

Problem. Den Raum jenseits aller Schwierigkeiten zubeanspruchen, den eine beliebige Monade durch ihren Wirkkreis besetzte, eingedenkt ihrer Einfachheit.

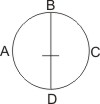Wenn wir zusammengestellt haben, auf welche Weise die Monade den begrenzten Raum erfüllt, wird dies für jedes andere beliebig begrenzte ausgedrückt werden können. Der Kreis ABCD stellt also das Raumsegment dar, das die Monade durch ihre Wirkung besetzt, BD sei der Durchmesser der Kugel ihrer Wirkung, d. i. die Entfernung, an der sie andere von weiterer gegenseitiger Annäherung abhält, die in B und D selbst anwesenden. Aber deswegen würde man zur Vorsicht geraten haben, daß dieser Durchmesser selbst der einer Monade ist, was jedenfalls unzutreffend wäre. Ebenso wenig ist auch irgendetwas unvereinbar mit unserem Annahme. Denn weil der Raum nur unter Berücksichtigung der Äußeren abgelöst würde, was auch immer an Substanz drinnen ist, d. i. die Substanz selbst, unterliegt der Abgrenzung der äußeren, die eigentlich nicht durch den Raum bestimmt werden, sondern deren eigene Abgrenzung auf deren Äußeren bezogen wird, diese nur im Raum zu suchen ist erlaubt. Aber, bejaht man die Anwesenheit einer Substanz in diesem Raumsegment, und daß sie überall in demselben vorhanden ist; warum zerteilt er [der Durchmesser] also die Substanz? Ich antworte: dieser Raum [der Wirkkreis der Monade] selbst ist umgeben von seinen außerhalb anwesenden Elementen. Wer also den Raum zerteilt, zerteilt die ausgedehnte Masse seiner Anwesenheit. Doch sind außer der äußeren Anwesenheit, d. i. die jeweiligen Abgrenzungen der anderen inneren [Substanzen], die wenn sie nicht wären, jene nicht haben würden, welchem sie anhängen, der Gegenstand. Aber die innereren sind nicht im Raum, deshalb weil sie innere sind. Und auch durch Teilung der äußeren Abgrenzungen werden sie selbst nicht geteilt. Man hat ebenso hierzu gesagt: Gott ist allen geschaffenen Dingen inwendig gegenwärtig durch die Tätigkeit der Erhaltung, wer also die Menge der erschaffenen Dinge teilt, teilt Gott, weil er die Umgebung seiner Anwesenheit teilt; so etwas äußerst unschickliches kann nicht im Bezug auf Gott gesagt werden. Daher erfüllt die Monade, die ein Element des einfachen Körpers ist, so weit den Raum, zumal sie zwar sonst eine ausgedehnte Größe hat, nämlich einen Umkreis der Wirkung, in dem aber nicht mehrere vorkommen, deren eins vom anderen getrennt, d. i. ohne andere selbst allein, eine eigene dauerhafte Beständigkeit hätte. Denn was im Raum BCD gefunden wird, von jenem, was im Raum BAD vorhanden ist, zu trennen ist also nicht möglich, damit ein beliebiges an sich erscheinen würde; weil beides bloß die Abgrenzung einer und derselben Substanz von den äußeren ist; aber das Accidens (das Prädikat) besteht nicht ohne eigene Substanzen. *)

*) Als größte aller Schwierigkeiten, die unseren Sätzen entgegenstehen können, wird angesehen was von der Darstellung der Bestimmungen der einen und derselben Substanz hervorgebracht worden ist. Denn die Wirkung der Monade, die im Raum BCD ist, ist außerhalb der Wirkung, die im Raum BDA ist, also werden sie wechselseitig von einander substanziell unterschiedlich gesehen und zwar was als außerhalb der Substanz anzusehen ist. Aber Beziehungen sind immer von sich aus gegenseitig und außerhalb der Substanz, weil jene Dinge, die auf die Substanz, auf die sie bezogen werden, sind von der Substanz und von einander vollkommen unterschiedlich, und das zeigt nicht die substanzielle Vielfalt.

Satz VIII.

Theorem. Die Kraft, durch die das einfache Element des Körpers seinen Raum besetzt, ist dieselbe, die sie anders Undurchdringbarkeit nennen; und wenn man sie nicht unterscheidet von jener Kraft, kann sie an diesem Ort sein.

Die Undurchdringbarkeit ist die Eigenschaft des Körpers, die benachbarte aus dem Raum, den er besetzt, fernhält. Weil aber der Raum, wie aus dem vorhergegangenen bekannt sein wird, den der Körper besetzt, (wenn man die Teile desselben ohne dazwischen gelagertes Vakuum eng miteinander verbunden versteht,) zusammengesetzt ist aus den Raumsegmente, die einzelne einfache Elemente enthalten; weil weiterhin das Eindringen der einzuschließenden äußeren Körper in den erfüllten Raum oder der Widerstand, der zur Undurchdringbarkeit erforderlich ist, zwar vielmehr eine gewisse Kraft erfordert würde, im Vorigen aber gezeigt worden ist, halten die Elemente, die ihren bestimmten Raum besetzen durch eine gewisse Wirkung das Eindringen von anderen dorthin ab; es ist offensichtlich, daß die Undurchdringbarkeit der Körper von nichts anderem außer von einer natürlichen Kraft der Elemente abhängt. Das war das Erste.

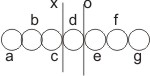Weiterhin sei die Linie a g mit einfachen Elementen der Materie, d. i. Monaden, erfüllt, wenn irgendein Element durch die Anwesenheit seiner Substanz bloß den Raum bezeichnen würde und den Raum nicht besetzen würde, würde der Ort d die gegebene Linie a g zweiteilen, und weil er so anzeigt, wo die eine Hälfte endet und die andere anfängt, wird er beiden Hälften gemeinsam sein. Aber die physikalischen Linien sind nicht gleich, wenn sie nicht aus einer gleichen Anzahl Elemente bestehen und wenn nicht auf beiden Seiten die Anzahl der Elemente in den Linien a c und e g gleich ist; also wird der Platz der Monade d den Linien a c, e g gemeinsam sein, d. i. die genannten Linien würden sich unmittelbar im angegebenen Ort begegnen und daher nicht das Element d die benachbarten e und c von der unmittelbaren Berührung abhält, das ist, es wird nicht undurchdringlich sein. Wenn man behauptet, daß der von der Monade d besetzte Ort nicht den Linien a c, e g gemeinsam ist, wird der Punkt x sein, wo sich die Linien a c und d g unmittelbar begegnen und o der, in dem sich die Linien a d und e g begegnen; weil daher die Ort der Monade d sich unterscheidet vom Ort x und ebenso vom Ort o, weil der Ort der unmittelbaren Berührung mit anderen gemeinsam sein würde, wie vorher gezeigt, hat man drei verschiedene Punkte x, d, o, die ohne Zweifel irgendeine Linie bestimmen. Die bezeichnte Linie wird deshalb durch die unmittelbare Anwesenheit der Monade d bestimmt, d. i. sie ist im bestimmten Raum gegenwärtig, und weil sie nur eine Stellung der Substanz [und] keinen Raum, sondern einen Ort besetzen könnte, ist es notwendig, daß ein gewisses anderes in der Substanz gegenwärtig sei, das ein Maß der Nähe von beiden Seiten in den berührenden Elementen bestimmt und eine irgendeine Kraft, die Näheren von der Annäherung der Elemente c und e abhält; aber einer Kraft kann bloß eine Kraft entgegengestellt werden; also verursacht die Kraft, durch die das Element des Körpers seinen Raum besetzt, die Undurchdringbarkeit. Das war das Zweite.

Teil II.

Die Neigungen der allgemeinen physikalischen Monaden zu erklären, in soweit sie in einiger Verschiedenheit die Natur der Körper verständlich machen.

Satz IX.

Definition. Die gegenseitige Berührung mehrerer Elemente ist die erzeugte Anwendung der Kräfte der Durchdringbarkeit.

Kurze Erklärung. Die Berührung wird allgemein durch die unmittelbare Anwesenheit definiert. Aber wenn man sogar sehr viele äußere einbezieht, (weil ohne diesen Zusatz wäre Gott, der allen Dingen unmittelbar, aber zu innerst inne wohnt, in der Berührung selbst zu erwarten,) doch wird die vollständige Bestimmung aller Teile kaum [möglich] sein. Denn nachdem also von anderen hinreichend bewiesen wurde, können die abgetrennten Körper trotzdem mit dem leeren Raum zusammen bestehen, und deswegen unmittelbar miteinander anwesend sein, obschon, ohne gegenseitige Berührung, diese Erklärung der Lücke wird ohne Zweifel verstanden werden. Ferner wird anscheinend von der großen unmittelbaren Schule Newtons nicht ohne Grund die Anziehung der Körper behauptet, auch wenn sie von einander zerstreut sind, deren gemeinsame Anwesenheit dennoch ohne gegenseitige Berührung möglich wäre. Wenn man außerdem behauptet, welche die Berührungen von selbst durch die Kenntnis der unmittelbaren Nachbarschaft anbieten, ist dir zunächst die Kenntnis dieser Anwesenheit zu erklären. Wenn man sie durch gegenseitige Wirkung erklärt, wie es gemacht wird, frage ich, worin besteht die Wirkung? Ohne Zweifel wirken die Körper durch ihre Bewegung. Allerdings geht die Bewegungskraft von einem gegebenen Punkt aus und stößt entweder andere von denselben an oder zieht sie an. Ferner wäre die Wirkung in der Berührung zu verstehen, was leicht offenbar wird. Denn wir sagen, der Körper der sich dem Körper mehr und mehr nähert bis sie sich gegenseitig berühren und die Undurchdringlichkeitskraft bemerkt, das heißt die Abstoßung. Also erzeugt die Tatsache wechselseitig entgegengesetzter Elementen die Wirkung und dazu die Gegenwirkung die Vorstellung der Ursache von deren Berührung.

Satz X.

Theorem. Die Körper würden sich nicht eines bestimmten Volumens nur durch die Kraft der Undurchdringlichkeit erfreuen, wenn nicht gleichzeitig eine andere innewohnende der Anziehung anwesend wäre, die mit jener gleichzeitig die Grenze der Ausdehnung bestimmt.

Die Kraft der Undurchdringlichkeit ist die Abstoßungskraft, die beliebige äußere von der weiteren Annäherung abhält. Weil diese Kraft dem beliebigen Element innewohnt, wird das aus ihrer Natur selbst verstanden werden können, warum mit dem Zuwachs der Entfernung, zu der sie ausgedehnt wird, die Stärke der Wirkung verringert wird, daß sie in gewisser gegebener Entfernung völlig Null sei kann von sich aus garnicht verstanden werden. Und wenn er daher nur bei dieser [Entfernung] still stünde, gäbe es gar kein Gefügung der Körper, allerdings würde nur durch die einander abstoßenden Teilchen und dem Körper kein umschriebenes Volumen durch die bestimmte Grenze feststehen. Es ist deshalb notwendig, damit diesem Drang etwas entgegengesetztes entgegengestellt würde, und in der gegebenen Entfernung gleiches, das dem besetzten Raum die Grenze bestimmt. Was der Abstoßung entgegen wirkt ist die Anziehung. Es ist dem beliebigen Element daher nötig außer der Undurchdringlichkeitskraft eine andere anziehende [Kraft], von der, wenn sie entfernt wird, sich bestimmte Volumina der Naturkörper nicht ergeben würden.

Kurze Erklärung. Die Gesetze beider Kräfte sind zu erforschen, der Anstoßung sowie der Anziehenden, die in dem Element sind, die Untersuchung ist allerdings ein schwieriges Unterfangen und würdig, die den scharfsinnigen Geist rastlos beschäftigen würde. Mir reicht es an dieser Stelle aus, deren mit großer Sicherheit bewiesenen Existent wiedergegeben zu haben, soweit es das Gesetz der Kürze erlaubt hat. Aber wenn es gefällt, dieser Frage gleichsam eine gewisse ausgedehnte Beachtung zu widmen, würde sie sich nicht umgekehrt zum Zuwachs [der Entfernung] abschwächen, weil die Abstoßungskraft von einem Punkt im innersten des Raumes, der von Elementen bestetzt ist, und nach außen hin wirkt, die Stärke entlang jenes Raumes zu bewerten sein, in den sie sich erstrecken? Denn die Kraft, die von einem Punkt in der bestimmten Wirkungskugel ausgeht kann nicht gefunden werden, wenn nicht alles, was innerhalb des gegebenen Durchmessers des Raumes wahrgenommen wird mit Wirkung erfüllt würde. Was von dieser Lehre offenbart wird. Denn wenn man sich vorstellen würde wie die Kraft sich entlang gerader Linien aus einer gegebenen Oberfläche ausbreitet, wie das Licht, oder auch gemäß [John] Keill′s Überlegung [Introduction to Natural Philosophy, 4. Aufl. London, S. 5] zur Anziehungskraft selbst, wird die Kraft im selben Verhältnis ausgeübt wie das Vielfache der Linien, die aus der Oberfläche gezogen werden können, das ist im Verhältnis der aktiven Oberflächen. [3. Keplersches Gesetz!] Wenn die Oberfläche unendlich klein wäre, wäre auch die Kraft unendlich klein, und wenn sie endlich ein Punkt wäre, wäre die Kraft genau Null. Daher bei aus einem Punkt auseinanderstrebenden Linien kann die Kraft, die sich ausbreitet, in gewisser Entfernung nicht nachweisbar sein. Und deswegen wird der Raum, in dem die wirken würde, nicht begriffen, wenn er nicht vollständig erfüllt ist. Aber die Räume sind kugelförmig, deshalb gehen die Entfernungen mit der dritten Potenz der Entfernung ein. Also weil diese Kraft, die durch den größeren [Teil] des Raumes zerstreut wird, sich im umgekehrten Verhältnis der [betrachteten] Räume abschwächt, wird die Undurchdringbarkeitskraft im umgekehten Verhältnis der dritten Potenz des Abstands vom Zentrum sein.

Gegen diese [Kraft] weil die Anziehung nämlich die Wirkung eben der Elemente ist, aber entgegengesetzt, wird die kugelförmige Oberfläche, in der sich die Anziehung in gegebener Entfernung auswirkt, das Ende davon sein; weil deren [der Oberfläche] Punkte, von denen man Linien in Richtung Zentrum ziehen kann, die Anzahl, und zwar sogar die Größe der Anziehung ist bestimmt, sie wird unter dieser Bedingung bestimmbar sein, und sie nimmt im umgekehrten Verhältnis zur Kugeloberfläche ab, d. h. mit dem Inversen des Quadrats der Entfernung.

Wenn also die abstoßende [Kraft] mit der dritten Potenz in der größeren Länge abzunehmen festgestellt wird, in irgendeinem Punkt des Durchmessers müssen notwendiger Weise Anziehung und Abstoßung gleich sein. Und dieser Punkt wird die Grenze der Undurchdringbarkeit bestimmen, und die Berührung der umgebenden Äußeren oder das Volumen; denn die von der Anziehung übertroffene Abstoßungskraft wirkt nicht darüberhinaus [über die Berührung].

Schlußfolgerung. Wenn man das Gesetz der innewohneden Kräfte bestimmt hat, wird man auch das gleiche Volumen aller Elemente ohne Unerschied der verschiedenen Arten erkennen. Denn weil es an der Sonne ist, können die Kräfte der Abstoßung und der Anziehung zusammen, weil ja ihr Unterschied der größte ist, der es sein kann, hier stärker, anderswo abgeschwächt sein, jedoch, weil die Abstoßungskraft doppelt so groß ist in der doppelten Entfernung, und die Anziehungskraft ebenso, und übereinstimmt, sind alle Bewegungskräfte des Elements, das spezifisch doppelt so schwer ist, im Verhältnis ihrer Stärke, immer sind die genannten Kräfte in der gleichen Entfernung gleich, solange gleiches Volumen des Elements zu bestimmen notwendig ist, so groß/viel als nur, sie sich von den bekannten anderen Kräften der Elemente durch einen Schritt/ein Grad unterscheiden.

Satz XI.

Definition. Die Trägheitskraft ist in einem beliebigen Element eine bestimmte Größe, die in unterschiedlichen [Elementen] höchst unterschiedlich sein kann.

Der bewegte Körper würde in anderen, die er trifft, keine Wirkung haben, und er würde von irgend einem unbestimmt kleinen Hindernis zurückgetrieben werden zur Ruhe, wenn er sich nicht der Trägheitskraft erfreuen würde, die sich bemüht im Zustand der Bewegung zu verharren. Die Trägheitskraft der Körper ist allerdings die Summe derTrägheitskräfte aller Elemente, aus denen er zusammengesetzt ist, (und diese nennt man Masse;) also würde ein beliebiges Element, das mit einer bestimmten Geschwindigkeit bewegt wird, wenn sie [die Geschwindigkeit] nicht durch die Trägheitskraft vergrößert würde, gar keine Bewegungswirksamkeit bewirken. Aber was auch immer es mit anderer Größe zu multiplizieren gibt, durch andere größere Faktoren, es ist selbst eine Größe, die bald größer, bald kleiner anderen zugewiesen werden kann. Also es kann von der Trägheitskraft eines beliebigen Elements anderen sowohl mehr als auch weniger gegeben werden in den verschiedenen Elementarten.

Erklärung I. Gegeben werden können den beliebigen Elementen von gegebenen anderen, deren Trägheitskraft, oder was unter anderem Umstand das gleiche ist, die Bewegungskraft, doppelt oder dreifach größer ist, d. h. die durch bestimmte Geschwindigkeit einer doppelt oder dreifach so großen Kraft widerstreben, und dieser durch die bewegte Geschwindigkeit mit doppelt oder dreifach größerem Schwung viel vermögen.

Erklärung II. Weil beliebige Elemente, ohne Unterschied der Art, jedoch durch das Volumen gleich zu bewirken stimmt mit der Erklärung des vorigen Satzes überein, und soweit im gleichen völlig erfüllten Raum immer die gleiche Anzahl Elemente enthalten ist, daraus wird richtig gefolgert: die Körper, wenn man sie vom meisten zugemischen Vakuum abtrennen würde und den ganzen vollständig erfüllten Raum annähme, (Gay-Lussac 1802, Avogadro 1811 für ideale Gase), dennoch können unter dem Volumen die unterschiedlichsten Massen zusammenhängen, allerdings mit Elementen mit mehr oder weniger Trägheitskraft versehen. Denn die Masse der Körper ist nicht, außer deren Größe ihrer Trägheitskraft, die entweder der Bewegung widersteht oder die gegebenen bewegten durch die Geschwindigkeit gewiß mit Schwung bewegt werden bewirken (Robert Hook 1635 - 1703).

Daher gilt die nicht immer ausreichend sichere Folgerung, von der kleineren Menge der Materie, die in dem gegebenen Volumen zusammengefaßt ist, zu geringerer Dichte und zu der größeren eingelagertes Vakuum. Jeder Körper von beiden kann entweder durch entsprechend eingelagertes Vakuum wirken, oder völlig dicht sein, und trotzdem [kann] einer von beiden weit mehr Masse haben; der Grund des Unterschieds beruht vollkomen auf der eigenen Eigenschaft der Elemente.

Satz XII.

Theorem. Der spezifische Unterschied der Dichte der Körper, die in der Welt beobachtbar sind, kann klar nicht ohne den Unterschied der spezifischen Trägheit seiner Elemente selbst erklärt werden.

Wenn alle Elemente sich der gleichen Trägheitskraft und des gleichen Volumens erfreuen würden, ist zum Verständnis den Unterschied des Mangels an Dichte der Körper das absolute Vakuum nötig, das den Teilen zugemischt ist. Denn es ist der Platz für die freie Bewegung und nicht wie in Newtons, Keills und anderer öffentlichen Darstellungen, nach solcher Theorie vollständig erfüllt. Und daher ist um die unendlich unterschiedliche spezifische Dichte der Materie zu erklären, z. B. des Äthers, der Luft, des Wassers, des Goldes, dem unmäßigen Belieben zu vermuten stattgegeben worden, durch die, das Gewebe selbst der Elemente welches der menschlichen Einsicht am weitesten fern liegt, unbedacht willkürlich erdacht wird, bald als kleinste Bläschen, bald nach Art der Zweige und verdrehten Brezeln diese uneingeschränkt und kühn sich vorzustellen, von welchem man sich die ausgedehnte Materie auf wunderbare Art und Weise und den naturgegebenen Raum von ein wenig Materie umgeben denken könnte. Aber erfahre, die Lehren über die sie streiten.

Die gewaltiger Menge dünner Fasern, oder Bläschen, die sie unter der Haut unermeßlicher Zartheit für die Menge der Materie als Vakuum verstehen, wird notwendiger Weise vom ständigen Zusammenschlagen der Körper und durch Reibung endlich zerrieben werden, und nach dieser Überlegung würden endlich kleine Stückchen der Zerriebenen das auffangende Vakuum erfüllen. Aus welchem Grund wird der himmlische vollständig erfüllte Raum auf irgendeine Weise durch die starke Trägheit erstarren, und alle Bewegung wird zur Ruhe gebracht werden.

Weil weiter gemäß dem Grundsatz so beschaffene spezifisch lockere Medien aus maximal ausgedehnten Teilen und mit großem Volumen ausgestattet bestehen wäre es nötig, endlich ist bekannt, daß unter der Bedingung durch jene Zwischenräumen der dichten Körper, die gemäß dem selben Grundsatz enger zusammengepreßt sind, durchlässig sein können, so wie das Feuer, das magnetische und das elektrisches Fluidum die Körper leicht durchdringen? Denn auf welche Art, die Teilchen, die mit größerem Volumen versehen sind in den Zwischenräumen, selbst in engen, sich selbst durchdringen könnten, weiß ich ebenso wenig wie die Unwissendsten nicht.

Wenn daher nicht der besondere Unterschied der einfachsten Elemente selbst, von der, von denselben im genau angefüllten Raum, bald durch weniger, bald weit mehr Masse aufgebaut werden kann, würde zugestanden werden, die Physik wird immer an dieser Schwierigkeit wie an einer Klippe hängen bleiben.

Satz XIII.

Theorem. Die Elemente des Körpers, auch die einzelstehenden, erfreuen sich in verschiedenen [Körpern] einer unterschiedlichen vollkommen elastischen Kraft, und sie bilden an sich das grundlegende elastische Medium und ohne Zumischung von Vakuum.

Jedes einfache Element, das den Raum durch die bestimmte Kraft seiner Anwesenheit besetzt, hält äußere Substanzen von ihm ab. Weil aber die beliebige Kraft eine endliche Größe hat, die von anderen größeren übertroffen werden kann, ist offensichtlich dieser abstoßenden kann eine andere stärkere entgegenstehen, welcher weil in deren Entfernung die innewohnende Kraft dem eingeschlossenen Element nicht zum Fernhalten genügt, es ist offensichtlich, daß jene in den besetzten Raum von selbst bis zu einer gewissen Grenze eindringen werden. Aber auf welche Weise die beliebigen Kräfte, die sich von einem bestimmten Punkt im Raum geradlinig ausbreiten mit der Vergrößerung der Entfernung abgeschwächt werden, daß diese Abstoßungskraft, die näher am Mittelpunkt der Wirkung hinzugefügt wird, von ihm aus stärker wirkt ist offensichtlich. Und weil die Abstoßungskraft, die in der gegebenen Entferung vom Zentrum der Abstoßung begrenzt ist, wächst sie im bestimmten Verhältnis der Annäherung, und muss am eigentlichen Punkt [der Ausgangs] unbegrenzt sein, ist offensichtlich, durch keine vorstellbare Kraft kann bis ins Innere des Elements vorgedrungen werden. Demnach wird es das vollkommene Elastikum sein und mehrere derartige bilden durch Elastizität das grundlegende elastische Medium. Daß diese Elastizität in verschiedenen unterschiedlich ist, ist offensichtlich nach der Erklärung zum Satz X.

Kurze Erklärung. Die Elemente sind vollkommen undurchdringlich, das heißt, durch eine noch so große äußere Kraft, die nicht im Stande ist sie vom innersten Raum, den sie besetzen, auszuschließen, die aber zusammenpressbar sind, und die auch größere Körper bilden, allerdings mit dem Zugeständnis des ein wenig zusammengedrückt werdens durch die äußere Kraft. Daher wäre es erlaubt, die Herkunft der Körper oder des grundlegenden elastischen Mediums, von welchen im Äther, oder der Feuermaterie im Vorigen^* zu äußern.

* Gemeint ist die Dissertation aus dem Jahr 1755: "Meditationum Quarundam De Igne"