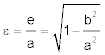Die Ellipse

Die typischen (terrestrichen) Navigationsaufgaben an der Küste und auf dem Großkreis gehen von einer Kugelgestalt der Erde aus. Die Grundlage ist die euklidische Geometrie. Mit dieser Vereinfachung macht man beim Navigieren in Küstengewässern Fehler in der Größenordnung von maximal einigen hundert Metern. Will man genauer Navigieren oder genauere Karten konstruieren, muss man die tatsächliche Form der Erde durch ein Ellipsoid annähern. Damit erreicht man Land- und Revier-Seekarten, die eine Ge­nauig­keit in der Größenordnung einiger Dezimeter haben. Die Annäherung der Erdoberfläche an ein Ellipsoid ist auch die Grundlage der satellitengestützten Navigation mit GPS (sowohl auf der Straße als auch auf See). Der Nachteil dieser Geo­metrie auf der Ellipse ist, dass man keine einfachen, mit dem Rechenschieber oder Taschenrechner zu lösende, Formeln mehr ableiten kann. Man braucht schon Computer. Diese Geometrie ist die nicht-euklidische Geometrie.

Für die terrestrische Navigation — bei der Entfernungen auf der Erdoberfläche berechnet werden — brauchen wir die Mittelpunktsgleichung der Ellipse in karthesischen und in Polarkoordinaten und die Schei­tel­glei­chung. Die Astronomie rechnet dagegen die Stellungen der Gestirne mit der Brenn­punkts­glei­chung in karthesischen und in Polarkoordinaten.

Die Geometrie der Ellipse

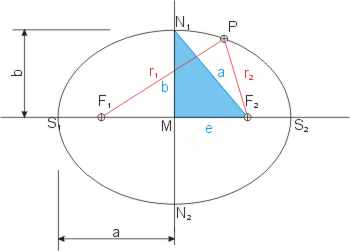Ellipse Betrachten wir die Ellipse. Jeder Punkt P auf ihr hat von zwei Punk­ten F1 und F2 den gleichen Ab­stand r1 + r2 = 2 · a. (Auf dieser Definition basiert die Gärt­ner­kon­struk­tion der Ellipse.) Die Ellipse sieht aus, wie ein gestauchter Kreis. Statt eines Radius gibt es zwei, die große (a) und kleine (b) Halbachse heißen. Die beiden Punk­te F1 und F2 sind die Brenn­punkte der Ellipse. Sie liegen auf der Hauptachse und die schneidet die Ellipse in den Haupt­scheiteln S1 und S2. Die Ne­ben­ach­se steht auf der Haupt­achse senk­recht und geht durch den Mit­tel­punkt M der Ellipse. Ihre Schnittpunkte mit der Ellipse sind die Nebenscheitel N1 und N2. Es gilt im rechtwinkligen blauen Dreieck der Satz des Pythagoras: a2 = b2 + e2.

Hinweis:Bei einer gegebenen Ellipse findet man die Brennpunkte als Schnittpunkte eines Kreises mit dem Radius der großen Halbachse um einen Nebenscheitel mit der großen Achse.

Die lineare Exzentrizität

Die Abstände der Brennpunkte F1, 2 vom Mittelpunkt sind gleich. Man nennt den Abstand MF1 = MF2 die lineare Exzentrizität e oder die Brennweite der Ellipse. Man berechnet e nach Pythagoras im recht­wink­ligen, blauen Dreieck. Da der Nebenscheitel N1 ein Punkt auf der Ellipse ist, beträgt sein Ab­stand von den Brennpunkten 2 · a. Die Hypotenuse im blauen Dreieck hat also die Läge a, die senk­rechte Kathete ent­spricht der kleinen Halbachse. Also gilt b2 + e2  = a2, oder:

  • lineare Exzentrizität

Die numerische Exzentrizität

Zur Navigation interessiert uns besonders der Abstand zweier Punkte auf der Ellipse. Aber schon die Be­rech­nung des Umfangs ist mit einfachen Mitteln nicht mehr zu bewerkstelligen. Das geht nur durch In­teg­rieren einer Differentialgleichung in Polarkoordinaten. Um die Formeln abzuleiten, brauchen wir noch die numerische Exzentrizität ε.

Ellipse mit Leitlinie Die numerische Exzentrizität ε ist definiert als Quotient aus linearer Exzentrizität e und der Länge a der großen Halbachse:

  • numerische Exzentrizität

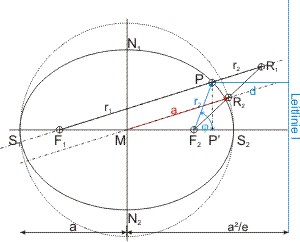
Die Leitlinie l ist geometrisch am Kegel erkenn­bar. Sie liegt parallel zur Nebenachse und schnei­det die Apsiden­linie (x-Achse) so, dass ihr Ab­stand vom Scheitel S2 sich zu dem des Brenn­punkts F2 verhält wie die große Halb­achse a zur linearen Exzentrizität. Ihr Ab­stand vom Mit­tel­punkt M der Ellipse ist a2 ⁄ e. Das Ver­hält­nis der Ab­stände jedes Punktes P auf der Ellipse vom Brenn­punkt F2 und dieser Leitlinie ist konstant r2 ⁄ d = konstant.

Die Leitlinie l hat vom Scheitel S2 den Abstand (a2 ⁄ e) - a, und ein Ellipsenpunkt P den Abstand d = a2 ⁄ e - x (x ist die x-Koordinate des Punktes P und entspricht der Strecke MP′). Die Ab­stände r1 und r2 des Ellipsenpunktes P von den beiden Brennpunkten F1 und F2 sind die Hypotenusen in den recht­wink­ligen Dreiecken F1PP′ bzw. F2PP′. Die beiden Dreiecke haben die Kathete y = PP′ ge­mein­sam, die an­de­ren Katheten haben die Längen F1P′ = 2·e + (x - e) und F2P′ = x - e.

Mit dem Satz des Pythagoras können wir nun zwei Gleichungen für die Kathete y aufstellen:

  • im Dreieck F1PP′: y² = r1² - (2·e + (x - e))²
  • im Dreieck F2PP′: y² = r2² - (x - e)²
  • damit:
  • r1² - (x + e)² = r2² - (x - e)²

Aufgelöst nach r1² und ausmultipliziert ergibt: r1² = r2² + 4·e·x, oder r1² - r2² = 4·e·x = (r1 + r2)·(r1 - r2).
Da r1 + r2 = 2·a kann man die vorige Gleichung dividieren und erhält r1 - r2 = 2·e·x ⁄ a. Oder nach Ein­set­zen der Definition der Ellipse und aufgelöst: r1 = a + e·x ⁄ a bzw. r2 = a - e·x ⁄ a.

Diese letzte Gleichung kann man auf beiden Seiten mit a multiplizieren und nach x auflösen: x = (a² - r1·a) ⁄e. Diesen Ausdruck für x setzt man in die Gleichung für den Abstand d des Ellipsenpunkts P von der Leit­linie ein, und erhält: d = r1·(a ⁄ e). Daraus die Beziehung d ⁄ r1 = a ⁄ e. Damit ist gezeigt, dass das Ver­hält­nis der Abstände eines beliebigen Ellipsenpunktes vom Brennpunkt und von der Leit­linie konstant ist, und nur von Parametern der Ellipse abhängt. Der Kehrwert dieses Verhältnisses wird nu­me­ri­sche Exzentrizität ε genannt. Anschaulich erkennt man die numerische Exzentrizität aus dem Bild der Entstehung der Kegelschnitte.

In der Abbildung oben iat auch eine geometrische Konstruktion der numerische Exzentrizität ein­ge­zeich­net. Man verlängert den Strahl vom entfernteren Brennpunkt F1 zum Punkt P auf der Ellipse um den Ab­stand von P zum näheren Brennpunkt r2, und erhält den Punkt R1. Der Schnittpunkt einer Pa­ral­le­len zu PR1 (= 2·a) durch den Mittelpunkt der Ellipse schneidet die Verbindungslinie von R1 und F2 im Punkt R2, der auch auf dem Umkreis der Ellipse liegt. MF2 = e und MR2 = a. Mit Hilfe eines Pro­por­tional­lineals kann man nun das Verhältnis e ⁄ a berechnen. (Edmund Gunter erklärt das ausführlich im 2. Buch des Sectors, Kap. II unter 5.)

Die Ellipse und ihr Umkreis

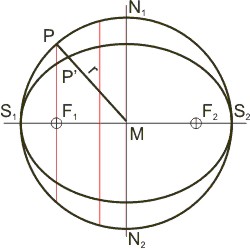Ellipsenparameter Die Ellipse ist ein affines Abbild des Kreises — man staucht den Kreis einlang einer der Achsen und er­hält die Ellipse. Daher spielt der Kreis, aus dem die Ellipse ent­stan­den ist, für viele Berechnungen der Ellipse nach der Euclidschen Trigonometrie eine aus­schlag­ge­ben­de Rolle. Beispiele sind Kepler, Newton und Gauss. Der Durchmesser des Umkreises ist gleich der großen El­lip­sen­achse, die Mittelpunkte von Ellipse und Umkreis fallen zusammen. Nach Appolonius von Perge verhalten sich die Sehnen von Ellipse und Kreis, die senkrecht auf der großen Achse stehen, wie die kleine zur großen Halb­achse der Ellipse. Die Sehne, die durch einen der Brenn­punkte der El­lip­se geht, heißt Ellipsenparameter 2·p. Man berechnet sie im rechtwinkligen Dreieck ΔP'F1M aus der großen und der kleinen Halbachse, a bzw. b, nach dem Satz von Pythagoras. Bekannt sind ja die Hypotenuse r = a und die Strecke MF1 = e (die lineare Ex­zen­tri­zi­tät); daraus erhält man die Länge der Halbsehne F1P', und die verhält sich zur Ellip­sen­halb­sehne F1P wie die große Halbachse der Ellipse a zur kleinen b.

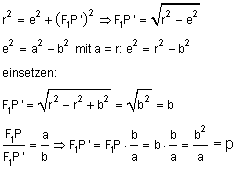
  • Formel Ellipsenparameter
  • Also: p = b² ⁄a.

Dieser Zusammenhang von Ellipse und Umkreis ermöglichte Kepler, seine Gesetze mathematisch abzuleiten (ebenso verwenden Newton und Gauss den "Ellipsenparameter").

Die sieben Bücher des Appolonius von Perge sind im Web zu finden.
Valid HTML 4.01 © Rainer Stumpe URL: www.rainerstumpe.de