Kartenprojektionen
Je nach Verwendungszweck der Karte wird die Erdoberfläche nach unterschiedlichen Algorithmen auf eine ebene (Karten-) Fläche projiziert. Für übliche Landkarten verwendet man die orthografische Projektion, für Seekarten die Mercatorprojektion und für Wetterkarten die gnomonische Projektion.
Landkarten entstehen aus der dreidimensionalen Vermessung (durch Triangulation) der Erdoberfläche. Die Höhen werden dabei relativ zu einem willkürlich festgelegten Höhenbezugspunkt angegeben. In Deutschland liegt dieser Punkt auf dem Brauhügel in Potsdam (heute: Wissenschaftspark). Von diesem Referenzpunkt aus ist Deutschland mit einem Netz geodätischer Punkte überzogen. Jeder triangulierte Punkt wird auf eine Bezugsfläche projiziert, das Bessel-Geoid (das in seiner Höhe durch den Höhenbezugspunkt gelegt wird). Als Gitternetzkoordinaten werden in Deutschland die Gauß-Krüger Koordinaten benutzt. Sie geben den Abstand in Metern vom Äquator (Hochwert) und einem Referenzmeridian (Rechtswert) an. Die Punkte auf dem Geoid werden dann, z. B. orthografisch, auf eine Kartenebene projiziert. Da Straßenkarten und Stadtpläne richtige Entfernungen angeben sollten, verwendet man hier spezielle Projektionsmethoden.
Jedes Land benutzt traditonell ein eigenes Geoid, das die tatsächeliche Landfläche optimal anpaßt und eigene Höhenbezugspunkte. Das ist natürlich nicht optimal, denn beim Anschluß der Karten zweier Länder muß man immer umrechnen. Deshalb wurde in der EU ein neuer Höhenbezugspunkt definiert: der Amsterdamer Pegel. Seit 1992 werden deutsche Karten auf diesem neuen Bezugspunkt bezogen (allerdings nur die neu erstellten). Ein weiterer Vorteil des einheitlichen Bezugspunktes ist die einheitliche Höhenangabe der Küstenregionen (europäische Seekarten beziehen die Meerestiefe schon länger auf den Amsterdamer Pegel).
Es ist offensichtlich, dass man Kartenanschlüsse nur durch Sichtverbindungen eindeutig zuordnen kann. Probleme gibt es zwischen Kontinenten, z. B. zwischen Europa und Amerika. Deshalb hat die International Geodetic Union (IGU) ein Geoid definiert; das derzeitig verwendete ist das Geoid WGS84. Nun kann man - mit Hilfe von GPS - den Bezug nationaler Landkarten über dieses Geoid herstellen. WGS84 wird auch für Seekarten als Referenzgeoid verwendet. Allerdings kann man auf hoher See nicht triangulieren, sodass es nur für die Satelitennavigation relevant ist. Das WGS84 schließt sich an die tatsächliche Gestalt der Erde bestmöglich an; die lokale Abweichung beträgt maximal 100 m. Für Europa betragen die Abweichungen zwischen 50 und 60 m, es gibt also ein Ellipsoid, das sich besser anschießt, das Bessel-Geoid.
Die orthografische Projektion
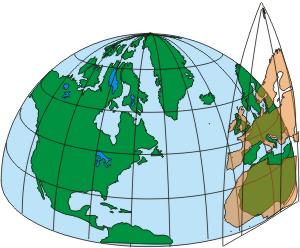
Bei der orthografischen Projektion wird die Kugeloberfläche wie eine Apfelsinenschale in Spalten abgeschält und eingeebnet. Diese Projektion ist flächentreu. Für Strassenkarten muss man aber eine Korrektur anbringen, um Entfernungen richtig abzubilden. In orthografischen Karten sind die Breitengrade gerade Linien, die Meridiane sind gebogen.
Die Mercator-Projektion
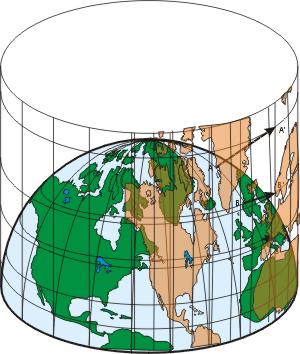
Der Vorteil der von Mercator in der Seefahrt eingeführten Zylinderprojektion — gegenüber der für Landkarten üblichen orthographischen Projektion — ist, dass die Verbindungslinie zwischen zwei Orten direkt den zu steuernden Kurs ablesen lässt: sie ist winkeltreu, bildet aber Flächen nicht richtig ab. Meridiane und Längengrade sind gerade Linien. Der Nachteil liegt in der mit steigender geographischer Höhe wachsenden Verzerrung von waagrechten Strecken auf den Breitenkreisen.
Bei der Mercator-Projektion wird aus Δφ ⇒ Δy und aus Δλ ⇒ Δx, wobeiΔx = Δλ ⁄ cos Δφ.
Nur der Massstab der Meridiane ist auf Seekarten verläßlich — wenn auch die Bogenminute je nach Breite unterschiedlich lang ist. Man kann also nur mit dem seitlichen Massstab einigermaßen zuverlässig "schräge" Entfernungen abgreifen. Sicherer ist die Entferungsbestimmung nach der Methode der mittleren Breite.
zurück zum SeitenanfangDie gnomonische Projektion
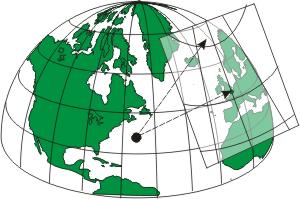
Bei der gnomonischen Projektion wird die Kugeloberfläche auf eine eben Tangentialfläche projiziert. Dabei kann man den Erdmittelpunkt (Wetterkarten, Seekarten) oder den Gegenpol als Ausgangspunkt des Projektionsstrahls verwenden. Die Längengrade sind gerade Linien, die Meridiane Ellipsen bzw. Hyperbeln mit ungleichem Abstand, wenn der Erdmittelpunkt verwendet wird, bzw. gleichem Abstand, wenn der Gegenpol der Anfangspunkt des Projektionsstrahls ist. Zugbahnen von Tiefdruckgebieten (auf Großkreiskurs) sind gerade Linien.
zurück zum SeitenanfangKartenkoordinaten
Bereits die frühen Hochkulturen haben ihre Einflussbereiche vermessen und Karten gezeichnet. Spätestens Eratosthenes legte über die Karten der damals bekannten Welt ein Rastergitter, das Gitter des Eratosthenes. Im 17. Jahrhundert wurden dann in Europa und den Kolonien Grenzen von Staaten und Landeigentum durch Vermessung festgelegt (Kataster). Das 18. Jahrhundert war geprägt von den Geodäten, die durch Triangulation und ein Netz von geodätischen Festpunkten die Oberfläche der Erde dreidimensional vermaßen. Das heißt, vor etwa 200 Jahren kannte man die Entfernungen zwischen den Punkten des Netzes in drei Dimensionen. Die Maschen des geodätischen Netzes sind Dreiecke, und wenn man von den drei Winkeln und den drei Seitenlängen des Dreiecks drei beliebige Stücke kennt, kann man die anderen, unbekannten, berechnen (s. Trigonometrie).
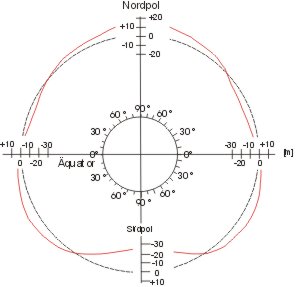
Alle Maschen (Dreiecke) des Netzes sind aber eben. Nun weiß man aber schon lange: die Erde ist annähernd eine Kugel. Man muss also um richtige Karten zu zeichnen, das dreidimensionale Maschennetz auf eine "kartoffelförmige" Oberfläche projizieren. Diese gekrümmte Fläche sollte die wahre Erdgestalt einer Region (z.B. Deutschland) möglichst genau wiedergeben. Um den Rechenaufwand im Rahmen zu halten, verwendet man ein Rotationsellipsoid. Das ist die Hüllkurve einer um die kleine Achse gedrehten Ellipse.
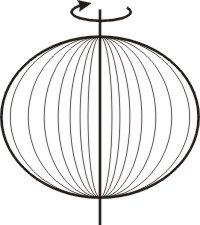
Da sich die Kenntnisse der Erdform über die Zeit geändert haben, gibt es eine Anzahl Ellipsoide, die für Karten verwendet werden. Sie unterscheiden sich zunächst in den Längen der Achsen. Man ist nun bestrebt, ein Land, z.B. Deutschland, möglichst ideal durch das Ellipsoid zu repräsentieren, verschiebt man die Lage des Rotationsmittelpunktes und die der Rotationsachse relativ zum Erd-(kugel-)radius und zur Erdachse. Das in Deutschland für Landkarten verwendete Ellipsoid wurde 1841 von Friedrich Wilhelm Bessel definiert.
|
|
||||
| Datum | Länder | Bezugspunkt | Große Achse (m) | Kleine Achse (m) |
|
|
||||
| WGS 84 | China, Russland, Hydrografisch, Aerografisch | Massezentrum der Erde | 6.378.137 | 6.356.752,3143 |
| Nord Amerika 1983 | Kanada, Kuba, USA und karibische US-Inseln | Massezentrum der Erde | 6.378.137 | 6.356.752,3141 |
| Ordnace Survey GB 1936 | GB, Nordirland | ? | 6.377.563,396 | 6.356.256,910 |
| Europa 1950 | Europa, Naher Osten, Nordafrika | Potsdam | 6.378.388 | 6.356.911,9462 |
| Deutschland | Deutschland | Potsdam | 6.377.397,155 | 6.356.078,9629 |
|
|
||||
|
Auszug aus: DEFENSE MAPPING AGENCY TECHNICAL MANUAL 8358.1 (1. Auflage 1990): http://earth-info.nga.mil/GandG/publications/tm8358.1/pdf/8358_1a.pdf |
||||
|
|
||||
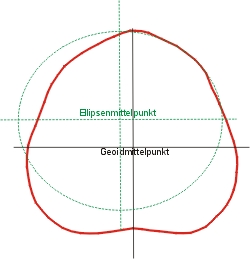
Seglern ist das WGS84, das ein 1984 festgelegtes mittleres Referenzellipsoid definiert, bekannt. Der Unterschied zum Bessel Geoid beträgt ca. 70 m. Das Ellipsoid berührt die WGS-84-Fläche in Rauenberg bei Potsdam. Sein Mittelpunkt ist gegenüber dem des WGS-84 606 m entlang der x-Achse, um 23 m entlang der y-Achse, und um 413 m entlang der z-Achse verschoben, und die Ellipsoidradien sind auch unterscheidlich.
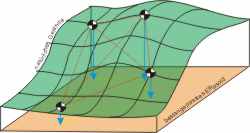
Bei der Kartenerstellung vermisst man zunächst die Oberfläche der Erde dreidimensional durch Triangulation. Diese physische Oberfläche wird auf ein Referenzgeoid projiziert. Dabei wählt man das Geoid, das der natürlichen Form der Erde unter der vermessenen Landfläche am besten angleicht. Mit dem Besselschen Geoid werden in Deutschland Karten erstellt, die auf ca. 10 cm genau die wirklichen Verhältnisse abbilden. Die auf das Referenzgeoid projizierte dreidimensionale Landschaftsbild wird nun in einer Kartenprojektion auf die Papierebene übertragen, die 3. Dimension erscheint als Höhenlinien. Bei der Projektion werden aus den Kugelkoordinaten elliptische Koordinaten und schließlich ein ebenes Raster.
Seekarten haben es da leichter. Die Meeresoberfläche kann schlecht 3-dimensional vermessen werden (inzwischen geht das auch mit Satelliten), und so sucht man ein Referenzgeoid, das einen hinreichend guten Anschluss an die nationalen Landkarten hat. Das ist bisher das WGS84. Die Projektion ist eine Mercator-Projektion.
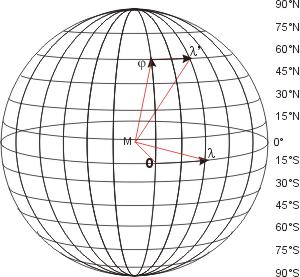
In Kugelkoordinaten werden Punkte auf der Erdoberfläche durch drei Werte repräsentiert:
- den Abstand vom Kugelmittelpunkt
- den Winkel entlang eines Hauptmeridians
- den Winkel entlang des Äquators
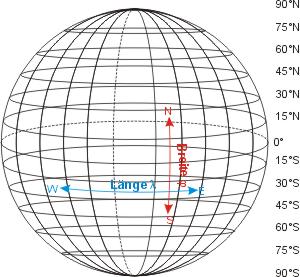
Durch die Transformation auf eine Kugel mit konstantem Radius werden die Winkel in Strecken (Entfernungen) von den Bezugskreisen umgewandelt. Diese Strecken kann man dann massstabsgetreu auf die Kartenebene projizieren.
Bei der Transformation werden die Strecken zwischen zwei Meridianen auf einem Kreis paralel zum Äquator immer kürzer, je weiter man sich einem Pol nähert. Die Mercator-Projektion der Seekarten korrigiert das durch eine Verzerrung. Sie ist winkelgetreu, gibt aber Flächen und Entfernungen nicht richtig wieder.