Ortsbestimmungen

Für eine sichere Fahrt muss man — wenigstens gelegentlich — seinen genauen Standort kennen. Dazu hat der Navigator folgende Möglichkeiten:

• die Bestimmung des Schiffsortes durch Kreuzpeilung,
• die Bestimmung des Schiffsortes durch Horizontalwinkel-Peilung dreier Objekte,
• die Bestimmung des Schiffsortes durch "Koppeln".
• die Bestimmung des horizontalen Gefahrenwinkels.

Weitere Standlinien findet er mit der Entfernungsbestimmung.

Die Kreuzpeilung

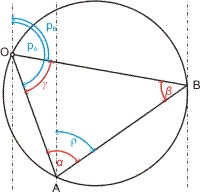
In der Sichtweite einer Küste bestimmt man den Schiffsort durch Kreuzpeilung von zwei Objekten A und B an Land, und trägt die Stand­linien in die Karte ein. Der Schnittpunkt der beiden Linien ist der Schiffsort O.

Man kann den Schiffsort O aber auch berechnen, wenn man zusätzlich zu den beiden rechtweisenden Peilwinkeln p_A und p_B auch die (Luftlinien-) Entfernung von A und B und die recht­wei­sende Richtung ρ ihrer Verbindungslinie (aus der Karte) kennt. Oder die Positionen von A (λ_A, φ_A) und B (λ_B, φ_B) sind bekannt, z. B. aus einem Küstenhandbuch. Dann kann man einfach und schnell mit dem Rechenschieber die Entfernung und die Richtung nach der Methode der mittleren Breite berechnen.

Der Schiffsort O muss auf einem Kreis mit AB als Sehne liegen. Nach dem Sehnensatz gilt für den Radius r des Umkreises: r = ½ · (AB ⁄ sin γ). Dabei ist γ = p_A - p_B.

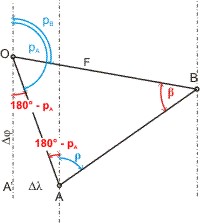
Mit ein paar Überlegungen zu "Winkeln an Parallelen" können wir den Winkel α bestimmen: α = ρ + (180° - p_A). Damit ist auch der Winkel β bekannt, denn die Summe der Innenwinkel im Dreieck beträgt 180°: β = 180° - α - γ.

Nun ist es möglich, die Längen der Dreiecksseiten AO und BO mit Hilfe des Sehnensatzes zu berechnen. Da uns aber die Position O interessiert, d. h. Δλ und Δφ relativ zur Position eines der gepeilten Objekte A oder B, brauchen wir nur den Abstand AO zu be­rech­nen: AO = 2 · r · sin β. Denn AO ist die Hypothenuse im recht­wink­ligen Dreieck A'AO, und wir erhalten:

• Δλ = AO · sin (180° - p_A) = AO · sin p_A
• Δφ = AO · cos (180° - p_A) = AO · (- cos p_A)

Beispielrechnung

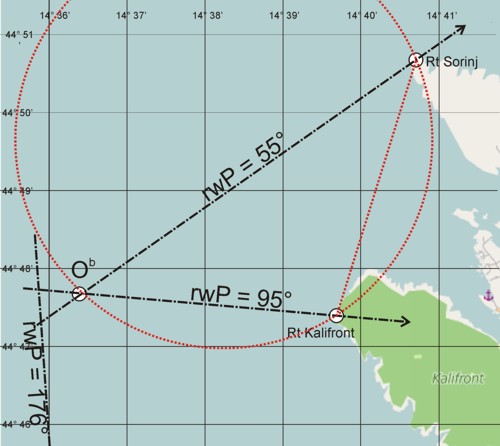
Ein Segelboot vor der kroatischen Küste peilt das Leuchtfeuer Rt Kalifront unter rw_KP = 95° und gleich­zeitig das Leuchtfeuer Rt Sorinj unter rw_SP = 55° (beide auf der auf der Insel Rab). Welche Position hat es?.

• Rt Kalifront, Fl. (3), 10s; φ = 44° 47,392′ N, λ = 014° 39,315′ E
• Rt Sorinj, Fl. 3 s.; φ = 44° 50,675′ N, λ = 014° 40,751′ E

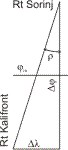
Zunächst berechnen wir die Richtung und die Entfernung der beiden Leuchtfeuer A (Rt Kalifront) und B (Rt Sorinj) nach der Methode der mittleren Breite:

• φ_m = (44,78₉₉° + 44,84₄₆°) ⁄ 2 = 44,81₇₂°
• Δφ = 3,28₃₀′
• Δλ′ = (14,67₉₂° - 14,65₅₃) ·cos 44,81₇₂ = 1,43₆₀′ · 0,70₉₄ = 1,01₈₆′
• tan ρ = 1,01₈₆′ ⁄ 3,28₃₀′ = 0,3103 ⇒ 17,2₃₇₉°
• c = Δλ′ ⁄ sin ρ = 1,01₈₆′ ⁄ 0,29₆₃ = 3,43₇₆′

Die beiden Leuchtfeuer sind also 3,44 sm von einander entfernt mit der rechtweisenden Richtung ρ = 17,2°. (Der Winkel ρ ist gleich der rw Richtung, da sie gegenüberliegende Scheitelwinkel sind.)

Als nächstes berechnen wir den Radius r des Umkreises und den Dreieckswinkel α bei Kalifront:

• r = ½ · 3,43₇₄′ ⁄ sin 40° = 2,67₃₈′.
• α = 17,23° + (180° - 95°) = 102,2₃₇₉° (er ist stumpf!).

• β = 180° - α - γ = 180° - 102,2₃₇₉° - 40° = 37,7₆₂₁°.
• b = 2 · 2,67₃₈′ · sin 37,7₆₂₁° = 3,27₄₈′

Den Winkel β kann man auch unabhängig von den Innenwinkeln mit den rw-Richtungen bestimmen: β = (180° - p_B + (180° - ρ) = p_B - ρ = 55° - 17,2° = 37,8°.

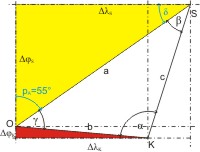
Es bleibt Δλ und Δφ in einem rechtwinkligen Dreieck (z. B. im gelben) zu berechnen. Im gelben rechtwinkligen Dreieck kennen wir den Winkel p_B, die Hypothenuse a können wir nach dem Sehnensatz berechnen:

• OS = a = 2 · r · sin α = 2 · 2,67₃₈′ · sin 102,23₇₉° = 5,22₆₁′.

Nun ist mit der Definition des Sinus und des Cosinus:

• Δφ_S = 5,22₆₁′ · cos 55° = 2,99₇₆′
• Die Breite des Schiffsorts O liegt also 3,04′ südlich von Rt Sorinj: φ_O = 44° 47,67.

• Δλ_S = 5,22₆₁′ · sin 55° = 4,27₆₀′
• Die Länge des Schiffsortes liegt also 4,28′ westlich von Rt Sorinj: λ_O = 014° 36,5′.

Die Zwischenergebnisse sind auf vier Nachkommastellen angegeben, wie man mit dem Taschenrechner rechnen würde. Der Ort stimmt mit dem durch Zeichnen auf der Karte ermittelten gut überein. Wenn man aber — zur Sicherheit — einen dritten Ort peilt (hier mit rwP = 176° den Leuchtturm Trstenik), gibt es drei Schnittpunkte der Peillinien. Irgendwo im resultierenden Dreieck mit ½ Seemeile Seitenlänge liegt dann der durch Peilung bestimmte Ort. Als vierte Standlinie kann dann der Umkreis über der Sehne dienen, was die Entscheidung über die Position erleichtern sollte.

Hübsch einfach mit dem Rechenschieber, gell?

Zur Überprüfung der Rechengenauigkeit — und zur Übung — berechnen wir die Position relativ zu Kalifront im roten Dreieck. Der Winkel μ bei O ergänzt die Peilung p_A von K zu 180°: μ = 180° - p_A = 85°, der Winkel ϑ bei K ist: ϑ = 90° - μ = 5°. Die Hypothenuse b im roten Dreieck ist oben schon berechnet worden: b = 3,27₄₈′

• Δφ_K = b · cos μ = 3,27₄₈ · cos 85° = 0,28₅₄′
• Die Breite des Schiffsortes φ_O liegt 0,28₅₄′ nördlich von Rt Kalifront: φ_O = 44° 47,67′
• Δλ · = b · sin 85° = 3,26₂₅′
• Die Länge des Schiffsortes λ_O liegt 3,26′ westlich von Rt Kalifort: λ_O = 014° 36,0′

Die bezüglich Rt Kalifort berechnete Länge des Schiffsortes weicht um 0,5 sm von von der relativ zu Rt Sorinj ab. Vermutlich handelt es sich um Rundungsfehler des Sinus nahe 90°. Zum Segeln reicht die Genauigkeit aber aus.

Der Ort, von dem man die Leuchtfeuer von Kalifront und Sorinj unter 95° bzw. 55° peilt, liegt also auf der Position: 44° 48′ N, 014° 34,6′E

Zur Überprüfung der Rechengenauigkeit — und zur Übung — berechnen wir die Position relativ zu Sorinj.

• α = 102,3° (s. o.)
• a = 2 · 5,38′ · sin 102,3° = 10,5′

• ---

• Δλ = 10,5′ · sin (90° - β) · cos 44,81° = 5,8′
• Δφ = 10,5′ · cos (90° - β) = -6,5′ 

• ---

• λ_O = 014° 40,751′ - 5,8′ = 014° 34,9′
• φ_O = 44° 50,7′ - 6,5′ = 44° 48,5′

Auch wenn man die Konstruktion des Schiffsortes aus den Peillinien in der Karte bevorzugt — weil man keinen Rechenschieber dabei hat, empfehle ich, den Standlinienkreis in die Karte einzuzeichnen. Das gibt zusätzliche Sicherheit und gibt einen Hinweis auf den Fehler, den man macht. Die Berechnung des Umkreisradius ist unter Horizontalwinkelpeilung erläutert.

Horizontalwinkel von drei Objekten

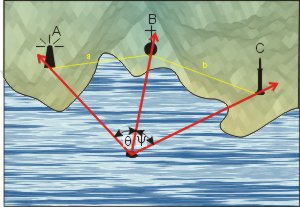
Diese Ortsbestimmung mit dem Sextanten ist völ­lig unabhängig vom Kompass und sehr ge­nau. Sie wurde 1692 von Laurent Pothenotfranzösischer Mathematiker, * um 1650 in Chaumont † 31.08.1732 in Paris, Professor am College Royal
Das Problem wurde von Willebrord Snellius um 1615 für die geodätische Triangulation formuliert. ein­ge­führt. Man peilt drei Objekte A, B, C an und misst mit dem Sextanten die beiden Win­kel θ und ψ. Der Karte entnimmt man die Ent­fer­nun­gen A-B und B-C (Hier liegt eine mög­liche Ungenauigkeit: die Kartendaten von See- und Land­karten stim­men nicht überein; man sollte darauf achten, dass die Land­mar­ken als See­zeichen mar­kiert sind! Sonst könnten sich ihre Ko­or­di­na­ten auf ein anderes Karten­datum be­zie­hen.). Der Schiffs­ort be­fin­det sich auf dem Schnitt­punkt zweier Kreise, die jeweils die Strecken AB bzw. BC als Sehne haben. Die Kunst ist es, die Mittelpunkte M₁ und M₂ die­ser beiden Kreis zu finden — die zu­ge­höri­gen Radien r₁ und r₂ sind dann ja die Strec­ken M₁A und M₂C und die Strec­ken M₁O_b und M₂O_b.

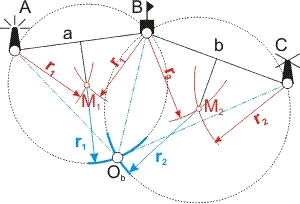
Die Lösung bietet der Sehnensatz. Nach Euklid ist der Winkel ∠AM₁B doppelt so groß wie der Winkel ∠AO_bB. Da wir im Dreieck AM₁B den gepeilten Winkel θ und die Basis AB (aus der Karte) kennen, und wissen dass AM₁ = BM₁ und ∠BAM₁ = ∠ABM₁ (gleich­schenk­liges Dreieck!), halbiert die Höhe h_M1 die Strecke AB. Also ist nach der Definition der Winkelfunktionen

• cos α = · (½ · AB) ⁄ AM₁ (α ist der Winkel im Dreieck AMB)
• und da der Winkel μ bei M im Dreieck AMB μ = 2 · θ und mit der Winkelsumme im Dreieck:
• α = β = ½ (180° - 2 · θ) = 90° - θ
• r₁ = AM₁ = M₁O_b = ½ · AB ⁄ cos (90° - θ) = ½ · AB ⁄ sin θ

Im Dreieck BM₂C erhält man mit der gleichen Argumentationskette:

• r₂ = CM₂ = M₂O_b = ½ · BC ⁄ sin ψ.

Man kann also die Radien r₁ und r₂ der Kreise um die Peilobjekte A, B und C mit dem Rechenschieber einfach berechnen, um A und um B je einen Kreis mit dem Radius r₁ schlagen, und um B und um C je einen Kreis mit Radius r₂. Dann schlägt man einen Kreis mit dem Radius r₁ um den Schnittpunkt M₁ und einen Kreis mit dem Radius r₂ um den Schnittpunkt M₂ deren Schnittpunkt ist der gesuchte Schiffsort O_b, dessen Koordinaten man der Karte entnimmt. Diese Methode ist unabhängig von Kompassrichtungen und GPS-Daten. Sie dient also zur Ermittlung der Kompassabweichung und zur Fehlerbestimmung der GPS-Ortsangaben.

Die Kombination von Rechnung und Konstruktion geht schneller als die reine Konstruktionslösung.

Das Verfahren ist ähnlich dem der unter Kreuzpeilung beschriebenen, das auch auf dem Sehnensatz beruht.

Beispielrechnung

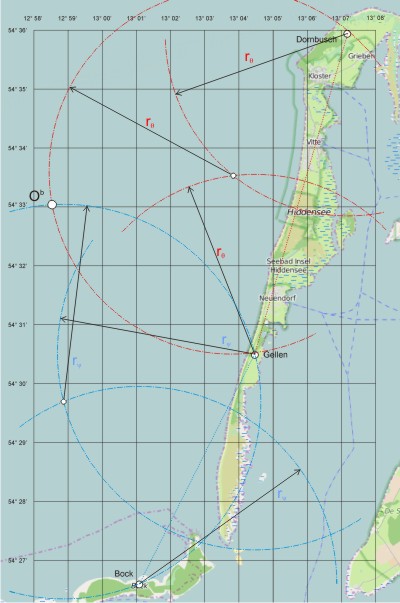
Ein Segelboot steht westlich von Hiddensee, der Kompass ist ausgefallen (das GPS auch). Man kann aber den Leuchtturm Dornbusch sehen, sowie die Leuchtfeuer Gellen und Bock. Welche Position hat das Boot?

• Dornbusch: φ 54° 35,948′ N. λ 13° 07,164′ E.
• Gellen: φ 54° 30,488′ N. λ 13° 04,466′ E
• Bock: φ 54° 26,591′ N. 7 13° 01,835′ E

Mit der Deckspeilscheibe werden die Winkel zwischen den drei Landmarken gemessen:

• ∠ Dornbusch O_b Gellen = θ = 67,0°
• ∠ Gellen O_b Bock = ψ = 38,3°

Zunächst werden die Mit­tel­senk­rech­ten auf den beiden Verbindungsstrecken errichtet. Man schlägt um jedes Leuchtfeuer einen Kreis mit und verbindet die Schnittpunkte der Kreise. Auf diesen Mit­tel­senk­rech­ten müssen die Mittelpunkte der beiden Kreise liegen, auf denen außer den Leuchtfeuern auch der Schiffsort O^b liegen (Sehnensatz).

Jetzt kommt der Rechenschieber zum Einsatz, denn die Konstruktion der Kreismittelpunkte ist umständlich. Als erstes werden die Länge der Strecken zwischen den Leuchtfeuern und deren rechtweisende Richtungen nach der Methode der mittleren Breite berechnet.

• Dornbusch → Gellen:
  • mittlere Breite φ_m = (φ_D + φ_B) ⁄ 2 = (54,599° + 54,508°) ⁄ 2 = 54,553° = 54° 33,21′
  • Breitendifferenz: Δφ = 5,46′
  • Längendifferenz: Δλ = 2,697′ · cos 54,553° = 1,564′
  • rw Richtung:
    1. tan δ = 1,564′ ⁄ 5,46′ = 0,286.
    2. ⇒ δ = 15,9°
  • Entfernung: c = 1,564′ ⁄ sin 15,9° = 5,71′
• Gellen → Bock:
  • mittlere Breite φ_m = 54,476° = 54° 28,547′
  • Breitendifferenz: Δφ = 3,90′
  • Längendifferenz: Δλ = 2,63′ · cos 54,476° = 1,529′
  • rw Richtung:
    1. tan ϑ = 1,529′ ⁄ 3,90′ = 0,392.
    2. ⇒ ϑ = 21,6°
  • Entfernung: d = 1,529′ ⁄ sin 21,6° = 4,15′

Die letzten Berechnungen sind die der Radien der Kreise zu den Sehnen Dornbusch → Gellen (r_θ) und Gellen → Bock (r_ψ):

• r_θ = ½ · c ⁄ sin θ = ½ · 5,71 ⁄ sin 67° = 3,10′.
• r_ψ = ½· d ⁄ sin ψ = ½· 4,15′ ⁄ sin 38,3°; =  3,35′

Jetzt werden noch die Kreise um die Leuchtfeuer mit dem jeweiligen Radius geschlagen und von deren Schnittpunkt ein Kreis mit dem gleichen Radius. Die beiden letzten Kreise schneiden sich im Schiffsort O^b. Die Position wird aus der Karte abgelesen φ = 54° 33,03′, λ = 12°58,54′.

Kann man die Position auch wie bei der Kreuzpeilung direkt berechnen? Man kann. Allerdings nicht mit einfachen Mitteln.

Ort aus Kurs und zurückgelegter Entfernung (Koppeln)

Das Koppeln des Schiffsortes ist ohne GPS die einzige Möglichkeit, eine Vorstellung von der gegen­wärtigen Position des Bootes zu bekommen, wenn keine Seezeichen oder Landmarken zum Peilen sichbar sind. Aus Gründen der Schiffssicherheit sollte man alle Stunden den Koppelort bestimmen — immerhin hilft eine auch ungefähre Position das Schiff im Notfall zu finden. Es ist sinnvoll, bei jeder Kursänderung einen Koppelort zu bestimmen!

Da ein Segelboot in einer Stunde keine großen Entfernungen zurücklegt, kann man die Be­rech­nungs­methode in der Kartenebene (Methode der mittleren Breite) anwenden. Ein Segelboot, das sich ohne Wind- und Stromversetzung mit konstantem Kurs und konstanter Geschwindigkeit v auf einem recht­wei­sen­den Kurs bewegt, wird sich von den Koordinaten des letzten bekannten Ortes in der Zeit t um eine Län­gen­dif­fe­renz Δλ und eine Breitendifferenz Δφ entfernt haben.

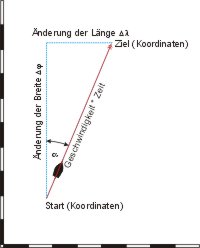
In dem ebenen, rechtwinkligen Dreieck sind bekannt die Länge der Hypo­tenuse c und der Kurswinkel α. Die Längenänderung Δλ ergibt sich dann aus der Definition des Sinus, die Brei­ten­än­de­rung Δφ aus der des Cosinus. Beides sind die Katheten des recht­wink­ligen Dreiecks.

• c = v · t
• Δφ = c · cos α
• Δλ = c · sin α

Ein bisschen Überlegung braucht die Umrechnung des rwK in den Dreieckswinkel, die von der Fahrtrichtung abhängt.

Die Kopplung ist ein Schätzverfahren, denn durch das Vernachlässigen von Versatz durch Wind und Strom macht man Fehler. Die Fehler addieren sich im Verlauf der Reise und es ist kein Wunder, wenn man schließlich einen Ort peilt, der weit weg ist vom Koppelort.

Beispielrechnung

Das Segelboot fährt mit 4,7 kn Kurs rwK = 60° von Norderney (O^b 53° 42′ N, 007° 10′ E). Wo steht es auf seiner Fahrt nach Helgoland nach 2 Stunden?

• c = 4,7 sm/h · 2 h = 9,4 sm
• Δφ = 9,4 sm · cos 60° = 4,7 sm

(wir erinnern uns: auf der Seekarte ist durch die Mercatorprojektion die Länge der Bogenminute von der (mittleren Breite abhängig!)

• Δλ · cos φ_m = (9,4 sm · sin 60°) · cos 53,7° = 4,8 sm = 4,8′

Das Boot ist also in seiner Position um 4,7′ nördlich und 4,8′ östlich vorangekommen. Die Koppelposition ist damit: O^k 53° 46,7′ N, 007° 14,8′ E.

Der horizontale Gefahrwinkel

Neben dem vertikalen Gefahrwinkel, der den mi­ni­ma­len Abstand von einem Objekt bekannter Höhe definiert, gibt es auch einen, der den Horizontalwinkel von zwei Objekten verwendet. Er verwendet Euklids Sätze über die Sehnen in Kreisen.

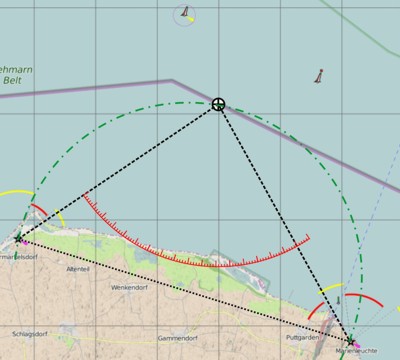
Man sucht einen Punkt auf der Karte, der den geringsten Abstand von einer Untiefe markiert, verbindet ihn mit den beiden Punkten die man peilen will, und misst den Winkel zwischen dne Verbindungslinien am Scheitel. Im Bild beträgt der Gefahrwinkel 85°. Peilt man nun mit dem Sextanten die beiden Objekte und misst einen kleineren als den bestimmten Gefahrwinkel, bleibt man sicher außerhalb der strich-punktierten Linie, denn alle Peripheriewinkel auf einem Kreis über einer Sehne sind gleich. Und der Peripheriewinkel schrumpft mit wachsendem Kreisradius.

© Rainer Stumpe, URL: www.rainerstumpe.de/
Datenschutzerklärung