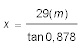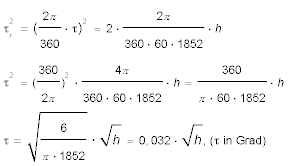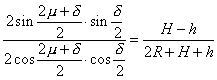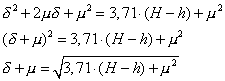Entfernungs- und Abstandsbestimmungen
Trigonometrische Abstandsbestimmungen gehören wohl zu den ganz alten Methoden. Schon als Kinder haben wir mit dem Augensprung Entfernungen geschätzt oder Winkel als Daumenbreite oder -länge gemessen. Der Navigator kennt außerdem noch folgende Entfernungsbestimmungen:
- mit Höhenwinkelmessung:
- mit Horizontalwinkelmessung:
Durch Höhenwinkelmessung
Objekt bekannter Höhe über der Kimm
Diese Entfernungsbestimmung basieren weitgehend auf der Anwendung der Regeln für das rechtwinklige Dreieck. Man kann aus der Messung eines Winkels und der Kenntnis einer Seitenlänge im rechtwinkligen Dreieck die anderen Seiten und den anderen spitzen Winkel berechnen. Der Winkel kann vertikal oder horizontal gemessen werden. Das (trigonometrisch) einfachste Beispiel ist die Entfernungsbestimmung aus dem Winkel unter dem man ein Objekt sieht — man braucht aber ein Präzessionsinstrument, auf See einen Sextanten.
- (Hinweis: alle Winkelangaben sind die gemessenen und um den Indexfehler des Sextanten korrigierten Winkel!)
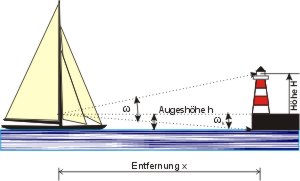 Man misst mit dem Sextanten z. B. einen Leuchtturm, dessen Höhe man aus dem Leuchtturmverzeichnis kennt (ACHTUNG: nachsehen, ob die First- oder die Galeriehöhe angegeben ist!) und korrigiert den
Indexfehler. Man schätzt seine Augeshöhe. Außerdem überzeugt man sich, dass man den Fuß des Objekts sehen kann (z. B. wenn man den Kamm brechender Wellen sehen kann; damit ist die Entfernung begrenzt auf die Kimmentfernung!).
Man misst mit dem Sextanten z. B. einen Leuchtturm, dessen Höhe man aus dem Leuchtturmverzeichnis kennt (ACHTUNG: nachsehen, ob die First- oder die Galeriehöhe angegeben ist!) und korrigiert den
Indexfehler. Man schätzt seine Augeshöhe. Außerdem überzeugt man sich, dass man den Fuß des Objekts sehen kann (z. B. wenn man den Kamm brechender Wellen sehen kann; damit ist die Entfernung begrenzt auf die Kimmentfernung!).
In dem rechtwinkligen Dreieck Auge-Leuchtturmfuß-Leuchtfeuer sind der spitze Winkel ω und die Gegenkathete bekannt, die Ankathete wird mit dem Tangens berechnet:
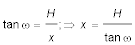 .
.- Wenn da nicht die Augeshöhe wäre!
Wegen der Augeshöhe ist nämlich das Dreieck nicht ganz rechtwinklig, weil man "von oben" auf den Fuß schaut — statt von gleicher Höhe. Da der Winkel ωK von der Entfernung abhängt, müssen wir ihn mit der ersten Entfernungsnäherung nach der gleichen Formel berechnen:
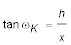 .
.
Der Winkel ωK wird nun vom gemessenen Winkel abgezogen und die korrigierte Entfernung x′ wird ausgerechnet:
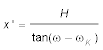 .
.
In Lehrbüchern findet man auch die Formel:
- Entfernung = 13 ⁄ 7 · (Höhe h in m) ⁄ (Winkel in ′) ≈ 1,857 · (Höhe h in m) ⁄ (Winkel in ′).
- (Hinweis: in englischen Lehrbüchern findet man den Faktor 1,854.)
Das ist im Prinzip die gleiche Rechnung, man erhält den Faktor 13 ⁄ 7, wenn man arc ω im Bogenmaß ausdrückt und die Umrechnung von m in sm durchführt.
Bisher ist noch nicht berücksichtigt, dass in Gezeitenrevieren die sichtbare Höhe größer (Ebbe) oder niedriger (Flut) sein kann als die in der Karte angegebene Höhe des Objektes. Auf welche Bezugsebene (Kartendatum) die Höhen bezogen sind, entnimmt man der Karte. Dann rechnet man den aktuellen Wasserstand aus und addiert oder subtrahiert den Unterschied zur Kartenbezugsebene zur Höhenangabe.
Beispielrechnung
Man misst einen Leuchtturm, dessen Leuchtfeuerhöhe 29 m beträgt wird bei einer Augenhöhe von 2,5 m unter dem Winkel ω = 52,7′ = 0,878°. Zu berechnen ist also
Für Winkel unter 5,5° benutzt man die Skala ST (arc) des Rechenschiebers. Zur Berechnung kehrt man die Gleichung um, da man die Winkelfunktion zuerst einstellen muss, und liest das Ergebnis auf der Skala CI ab. Läufer über 0,878 auf Skala ST, 29 auf Skala C unter den Läufer, Läufer auf Skala C 10, Zunge in Ausgangsposition (C1 über D1) und auf Skala CI den Wert ablesen (1892). Läufer auf Skala D 1892, Skala C 1852 unter den Läufer, Unter der 1 auf Skala C auf Skala D den Wert (sm) ablesen: 1,021. Zur Korrektur berechnet man nun ωK: über 2,5 auf Skala D stellt man 1892 auf Skala C; Läufer über 1 auf Skala D und auf der Skala ST ωK = 0,0757° ablesen. Der gemessen Winkel muss also um 4,5′ verringert werden. Die richtige Entfernung für 52,7′ - 4,5′ = 48,2′ = 0,713° ist 1,258 sm. Die Entfernung ist also durch die Korrektur größer geworden.
Der vertikale Gefahrwinkel
Die hier abgeleitete Formel für den Zusammenhang zwischen Entfernung zu einem Objekt an Land und der gemessenen Höhe des Objekts kann man auch als Mindestentfernung einsetzen, wenn man an der Küste mit einem Kartenobjekt bekannter Höhe mit vorgelagerter Untiefe vorbei segelt. Der Karte entnimmt man die Entfernung vom Objekt, die eine sichere Passage garantiert. Aus dieser Entfernung sieht man das Objekt unter dem Winkel ω:
- Winkel in ′ = (13 ⁄ 7) · (Höhe in m ⁄ Entfernung in sm)
Wird der im Verlaufe der Passage der Untiefe gemessene Winkel größer als der Gefahrwinkel, so ist man näher an der Untiefe als geplant. Solange er kleiner bleibt, ist man in sicherem Wasser.
Ebenfalls hilfreich ist der horizontale Gefahrwinkel, weil er genauso die Entfernungsmessung auf eine Winkelmessung reduziert.
Feuer in der Kimm
Nähert man sich in der Morgendämmerung einer Küste und sieht ein Leuchtfeuer, das im Leuchtfeuerverzeichnis beschrieben ist, kann man sehr einfach einen Schiffsort bestimmen. In dem Augenblick, in dem man die Feuerquelle sieht, ist die Entfernung genau definiert. Zusätzlich hat man die Peilung zum Leuchtfeuer. Man erhält eine gepeilte Standlinie und einen Entfernungskreis.
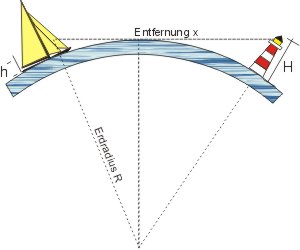
Es gilt sowohl für die Augeshöhe wie für die Leuchtfeuerhöhe die Berechnung der Kimmentfernung. Die Entfernung x der beiden Objekte ist dann die Summe der beiden Kimmentfernungen.
- x = x1 + xsub>2
- x1 = arccos[R ⁄ (R + h)] · 60 · 1,08)
- x2 = arccos[R ⁄ (R + H)] · 60 · 1,08).
(Der Faktor 1,08 ist die Korrektur für die Refraktion von ca. 8 %!)
Diese Rechnung kann man nicht mit dem Rechenschieber ausführen, der Erdradius R = 6.371.000 m hat zu viele signifikante Stellen — man braucht einen Taschenrechner. Zum Glück gibt es eine Faustformel:
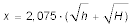
- (h und H im Metern, Ergebnis in Seemeilen).
Beispielrechnung
Auf dem Vordeck stehend (Augeshöhe 5,5 m) haben wir ein Leuchtfeuer in der Kimm gepeilt (Uhrzeit notieren!). Da wir die Kennung des Feuers bereits ausgezählt haben und den Leuchtturm im Leuchtfeuerverzeichnis identifiziert. Die Feuerhöhe beträgt 98 m.
Nun zücken wir den Rechenschieber und ziehen die Wurzeln aus 5,5 und 98. Läufer über 5,5 auf A stellen, unterm Läuferstrich auf D ablesen: 2,345; Läufer über 98 auf A, auf D ablesen: 9,81. Die beiden Zahlen im Kopf addieren: 12,15. Die 1 der Skala C über 1212 auf D stellen, und den Läufer über 2075 auf C schieben. Unter dem Läufer liest man auf D ab: 2515. Im Kopf überschlagen:2 mal 12 ist 24. Die Entfernung ist also 25 sm. Nun noch die rechtweisende Peilungslinie in die Karte eintragen und um das Feuer einen Kreis mit Radius 25 sm schlagen. Der Schnittpunkt ist der beobachtete Ort zum Zeitpunkt der Sichtung. Jetzt kann man wieder Koppeln.
Kimmtiefe
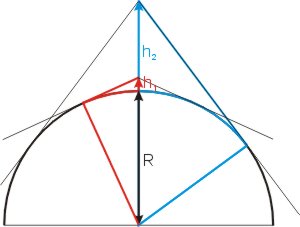
Aus der Astronavigation kennt man den Begriff der "Kimmtiefe". Das ist der Winkel τ zwischen der Horizontalen (scheinbarer Horizont) und der Blickrichtung zur Kimm. In der Abbildung ist der Zusammenhang des Winkels τ von der Augeshöhe h für zwei unterschiedliche Höhen dargestellt (h1 und τ1 bzw. h2 und τ2).
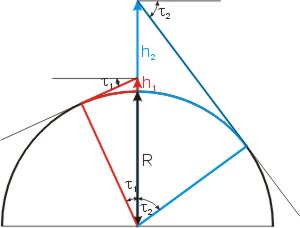
Der Kimmtiefe τ entspricht im Bogenmaß die Länge des Bogens zwischen dem Fuß des Beobachters und der Kimm (= Berührungspunkt der Blicktangente mit der Erdkugel). Denn die Schenkel der Winkel am Auge des Beobachters und am Erdmittelpunkt stehen paarweise aufeinander senkrecht. Der Winkel (90° - τ) ist daher der spitze Winkel im rechtwinkligen Dreieck, und deshalb ist
- sin (90° - τ) = R ⁄ (R + h) = cos τ.
Da cos τ sehr klein ist, rechnet man in Bogenminuten um (· 60) und hat die Kimmentfernung in sm. Diese Methode hat den Vorteil, man kann die Refraktionskorrektur anbringen. Das ist in Bogenminuten ja 1 ⁄ 12 oder 8% der Entfernung in sm. Man zählt also 8% zu
- R ⁄ (R + h) · 60 dazu.
Das Seglerlexikon von Joachim Schult (Delius Klasing, 1998) gibt eine Faustformel für den Winkel τ (in Grad, Augeshöhe in Metern):
-
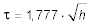 .
.
Die Wurzel der Augeshöhe entsteht durch folgende Näherung. Für kleine Winkel (< 5°) kann man für den Cosinus eine Näherungsformel anwenden:
 .
.
Für R setzen wir in Metern:
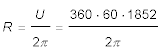 ,
,
da der Erdumfang ja 360 ⁄ 60 Seemeilen umfaßt. Die beiden Formeln werden zusammengeführt:
-
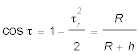
- und nach τr aufgelöst.
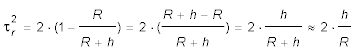 .
.
Da h sehr viel kleiner ist als R, setzen wir für R + h nur R. Für R setzen wir den obigen Ausdruck ein:
Hierbei ist die Refraktion noch nicht berücksichtigt. Dazu müssen wir τ in Bogenminuten umrechnen und 8% abziehen (wir sehen ja wegen der Refraktion weiter, und der Winkel kommt zu groß heraus). Multiplizieren wir also den Faktor 0,032 mit 60 und dividieren wir durch 1,08. Das Ergebnis ist 1,777; sollte das Seglerlexikon in seiner 10. Auflage einen Druckfehler haben? Es hatte, und er ist in neueren Auflagen korrigiert.
Beispielrechnung
Bei einer Augeshöhe von 2,5 m (sitzend im Cockpit) beträgt die Kimmtiefe in Bogenminuten arccos(6.371.000 &fradl; 6.371.002,5) = 0,051° = 3′. Man sieht man den Horizont in der Kimmentfernung von 3′ · 1,08 = 3,29 sm (mit dem Taschenrechner). Nach der Faustformel ergibt sich 3,28 sm (mit dem Rechenschieber), in der Kimmentfernungstabelle aus der Admirality List of Lights findet man 3,2 sm.
Kimmentfernung
Auf der Kugel hängt die Entfernung zum sichtbaren Rand (Horizont, Kimm) von Radius der Kugel und von der Höhe des Betrachters ab.
Die Sichtlinie ist die Tangente der Kugel (Kreis) und der Radius zum Berührungspunkt der Tangente steht auf der Tangente senkrecht. Wir erhalten also ein rechtwinkliges Dreieck Auge - Kimm - Erdmittelpunkt. Die Entfernung Auge - Kimm rechnen wir mit dem Pythagoras aus (geht nicht mit dem Rechenschieber, aber mit dem Taschenrechner):
-
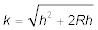 .
.
Zur Berücksichtigung der Refraktion addieren wir 8% (oder 1 ⁄ 12) der Entfernung. Es gibt auch eine Faustformel für die Kimmentfernung:
-
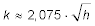 .
.
Diese Formel ähnelt der für die Kimmtiefe, nur der Faktor ist unterschiedlich:
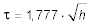 .
.
Von der Kimmtiefe zur Kimmentfernung hatten wir eine Refraktionskorrektur von +8% angebracht. Die Faustformel korrigiert mit +16%. Zwischen diesen beiden Werten wird die Wahrheit liegen, aber wo dazwischen sie liegt, hängt von der Lufttemperatur und der -feuchtigkeit ab. Beide Methoden sind nur Schätzungen mit einer großen Unsicherheit. Trotzdem kann man herrlich über die dritte Kommastelle des Faktors streiten.
Rechenbeispiel
Bei einer Augeshöhe von 2,5 m (Erdradius 6.371.000 m) erhält man eine Kimmentfernung von 6.095 m = 3,29 sm. Nach der Faustformel erhält man 3,28 sm.
Objekt bekannter Höhe teilweise hinter der Kimm
Ist es möglich, aus der bekannten Höhe eines Berges, der teilweise hinter der Kimm liegt, durch Messen des Winkels, unter dem man den sichtbaren Teil sieht, dessen Entfernung zu bestimmen? Im Admirality Manual of Navigation von 1955 fand ich einen Hinweis auf eine Tabelle (Lecky′s Tables), die einen Zusammenhang zwischen der beobachteten Höhe eines teilweise vom Horizont verdeckten Berges und seiner Entfernung angegeben hatte. Aber in einer neueren Ausgabe (1995) von Bowditch: The Practical American Navigator findet sich kein Hinweis mehr auf dieses Problem. Aber in der Ausgabe von 2002 ist die Tabelle wieder enthalten! Die Amerikaner hatten 1950 schon Computer, und konnten das Problem nummerisch lösen und eine Tabelle erstellen. Mich interessierte aber das trigonometrische Problem. Mehr als 2 Jahre nachdem ich es dargestellt hatte, erhielt ich von einem Besucher dieser Seite einen Ansatz zur Ableitung einer Formel. Kurz darauf hatte ich auch eine Kopie des "Lehrbuch der Navigation" 2. Auflage, herausgegeben vom Reichs-Marine-Amt im Jahre 1906, erhalten.
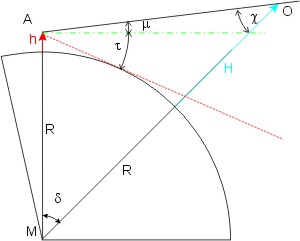
Betrachten wir die Skizze die Skizze des Problems: die waagrechte (Hilfs-)Linie (grün) geht vom Auge des Betrachters genau waagerecht auf den Berg zu. In der Skizze sind H die bekannte Höhe des Objektes, h die Augeshöhe, R der Erdradius, δ ist die Entfernung zum Objekt in Bogenminuten, τ die Kimmtiefe. Die Winkel μ und χ sind nur Hilfswinkel; sie kürzen sich in der arithmetischen Formelarbeit wieder heraus. (Im Grunde sind sie dazu da, ein rechtwinkliges Dreieck zu erzeugen.)
Der Winkel ∠MAO = 90° + μ, der Winkel ∠AMO = δ, und der Winkel ∠AOM = χ =
= 180° - ∠MAO - ∠AMO = 180° - 90° - μ - δ =
= 90° - (μ + δ) (Winkelsumme im Dreieck!).
Jetzt wendet man den Sinussatz an:
Die Seiten eines schiefwinkligen Dreiecks verhalten sich wie die Sinuswerte der den Seiten gegenüberliegenden Winkel.
und erhält die Gleichung
für die beiden Seiten MA = R + h und MO = R + H. Und durch Umformen (Trennen der Winkelfunktionen) ergibt sich:
Nun folgt eine etwas unübersichtliche arithmetische Umformung (Additionstheoreme!) mit dem Ziel, die Sinus- und Cosinusfunktion in eine Tangensfunktion umzuwandeln. Die wesentlichen Schritte sind:
Schliesslich erhält man:
In dieser Formel kann man die Größe von H + h gegenüber 2 · R ohne großen Fehler vernachlässigen;, und da μ und δ naturgemäß klein sind, kann man ohne großen Fehler schreiben tan (μ + δ ⁄ 2) = (μ + δ ⁄ 2) · sin 1´ bzw. tan (δ ⁄ 2) = (δ ⁄ 2) · sin 1´. Man erhält also den vereinfachten Ausdruck:
Der wird wieder umgeformt (Division durch sin 1´·sin 1´, Multiplikation mit 2):
Der Bruch enthält nur Konstanten (R = 6.378.137 m) und kann als Faktor 3,71 angegeben werden. Gleichzeitig addiert man zu beiden Seiten der Gleichung μ2:
Da der gemessene Höhenwinkel α des Objektes sich als Summe darstellt, erhält man μ = α - τ. Diesen Ausdruck substituiert man und löst nach δ auf:
Mit dieser Formel berechnet man die Entfernung δ zum Objekt in Bogenminuten (= sm!) aus der bekannten Höhe H (in Metern) des Objektes, dem gemessenen Höhenwinkel α (in Bogenminuten) und der Kimmtiefe τ (in Bogenminuten). Die Kimmtiefe in Abhängigkeit von der Augeshöhe (in Metern) entnimmt man einer Tabelle, oder man berechnet sie mit dem Rechenschieber.
Will man die Refraktion berücksichtigen, ändern sich die Faktoren in der Gleichung:
Da die Höhe eines Berges in Metern auf einer Insel i. d. R. vierstellige Zahl ist, die Augeshöhe aber ein- oder zweistellig, muss man mit 4 signifikanten Stellen rechnen. Das übersteigt die Rechenschiebergenauigkeit, und man rechnete (umständlich) mit der Logarithmentafel. Meist kann man aber nicht sicher sein, ob der Berg nun in der Kimm oder hinter ihr seinen Fuß hat. Also mißt man zunächst den Winkel α, und überschlägt die Entfernung mit der Formel für ein Objekt vor der Kimm: δ1 = (13 ⁄ 7) · (H ⁄ α). Dann berechnet man die Kimmentfernung für die Augeshöhe h mit der Faustformel: δ2 = 2,075 · √h. Ist δ2 > δ1, so liegt der Berg diesseits der Kimm, und man hat die Entfernung schon. Ist dagegen δ2 < δ1, suche man die Logarithmentafel …
Rechenbeispiel aus den Lehrbuch des Reichs-Marine-Amts
Man maß auf S. M. S. Moltke im Süden von Gran Canaria den Höhenwinkel des Piks von Teneriffa, Höhe 3.717 m, bei 8,3 m Augeshöhe zu 1° 34,5′. Wie war der Abstand?
- (H - h) = 3.717 - 8,3 = 3.708,7
- α = 94,5′
- τ = 0,032 · √8,3. = 0,092° = 5,53′
- unter Berücksichtigung der Refraktion: τ = 5,53′ ⁄ 1,08 = 5,12′
- (α - τ) = 89,4′
Es muss also der Ausdruck δ = √[3,71 · 3.708,7 + (89,4′)2] - 89,4′ berechnet werden. Mit dem Taschenrechner erhält man δ = 58,1′ = 58 sm. (Das Lehrbuch erhält mit der Logarithmentafel 60 sm.) Mit dem Rechenschieber (hier wird der UNIQUE-Navigator von Burns Snodgrass verwendet) — der ist ja jenseits seiner Rechengenauigkeit von 4 signifikanten Stellen — berechnet man zuerst die beiden Summanden unter der Wurzel:
- (α - τ)2: man stellt auf der x-Skala B 894 ein und liest auf der x2-Skala 7995 ab, Ergebnis 7995
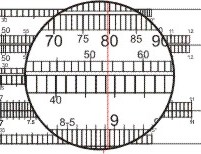
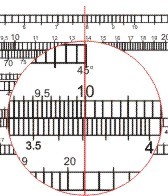
- [3,71 · 3.708,7: man schiebt die 10 auf der x-Zungenskala über 371 auf der x-Skala des Körpers und liest unter 3709 auf der Zunge auf dem Körper ab 1379, ergibt 13.790:
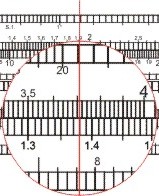
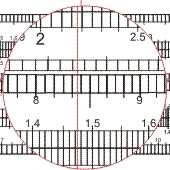
- Die beiden Zahlen werden addiert: 21.785; diesen Wert auf der x2-Skala eingestellen und auf der x-Skala ablesen: 147,4.
- Hiervon noch (α - τ) = 89,4′ abgezogen, ergibt eine Entfernung vom 58′ (= sm).
Es ist wohl eher ein Zufall, dass der Rechenschieberwert und der Taschenrechnerwert gleich sind, sicher ist kein Beweis für die Genauigkeit des Rechenschiebers.
Achtung: egal mit welchem Hilfsmittel gerechnet wird: diese Entfernungs"messung" ist eher eine Schätzung!
Durch Horizontalwinkelmessung
Versegelungspeilung
Bei der Versegelungspeilung fährt man mit konstanter Geschwindigkeit und konstantem Kurs eine zeitlang an einem Objekt mit bekannter Position, z. B. einer Tonne oder einer Landmarke, vorbei. Da man keine 2. Peilung hat kann man nicht unmittelbar einen Schiffsort bestimmen. Mit Hilfe des Sinussatzes lässt sich aber der Abstand zur Tonne, an der man vorbei gesegelt ist, berechnen.
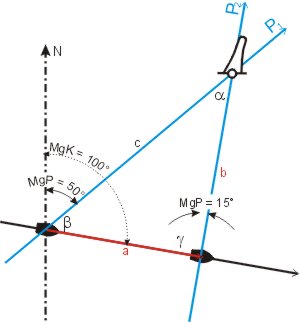
Das Boot fuhr mit rwK 100° und einer Geschwindigkeit von 6,5 kn zwischen der ersten Peilung (rwP1 = 50°) bis zur 2. (rwP2 = 15°) 1 ¼ Stunde (75 min). Die Strecke a ist damit 8,125 sm lang (zur Erinnerung: das geht toll mit dem Rechenschieber zu lösen!). Die beiden anderen Dreiecksseiten b und c stehen zu der bekannten Entfernung a nach dem Sinussatz mit den Winkeln im Verhältnis.
Für die Entfernung zum Feuer bei der ersten Peilung gilt:
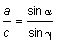 ,
,
für die bei der 2. Peilung entsprechend
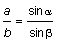 .
.
Jetzt folgt ein wenig Winkelarithmetik um die Winkel β und γ aus dem Kurs und den Peilungen zu berechnen.
- β = Kurs - Peilung 1 = 100° - 50° = 50°;
- für γ kann der Außenwinkel zu 100° - 15° direkt erkannt werden, damit ergibt sich
- γ = 180° - 85° = 95°;
(geht auf dem Rechenschieber nicht einzustellen! Aber es gilt sin (180° - α) = - sin α, wir können also mit sin (180° - 95°) = sin 85° rechnen).
Der Winkel α ergänzt die Summe der beiden anderen zu 180° (Winkelsumme im Dreieck):
- α = 180° - 50° - 95° = 35°.
Hinweis: Wenn man eine Seiten- bzw. Bordpeilung macht, also den Winkel zur Bootsachse misst, kann man sich die aufwändige Winkelberechnung sparen: man liest die Winkel β und γ direkt ab.
Beispielrechnung
Aus der Gleichung
erhält man den Ausdruck für die Länge von c:
- c = a · sin γ ⁄ sin α = 8 sm · sin 85° ⁄ sin 35° = 13,9 sm
sin 35° ablesen und notieren (wird noch einmal gebraucht). Läufer auf 35° Skala S, auf Skala D ablesen: 0,574. Läufer auf 85° auf Skala S, 10 auf Skala C unter den Läufer, Läufer auf 8 (Skala C), 0,574 (Skala C) unter Läufer, bei 1 (Skala D) auf Skala C ablesen: 13,9 sm.
Aus der Gleichung
erhält man den Ausdruck für b:
- b = a · sin β ⁄ sin α = 8 sm · sin 50° ⁄ sin 35° = 10,65 sm
Läufer auf 50° auf Skala S, 10 auf Skala C unter den Läufer, Läufer auf 8 (Skala C), 0,574 (Skala C) unter Läufer, bei 1 (Skala D) auf Skala C ablesen: 10,65 sm.
Die Entfernung zum Feuer betrug bei der 1. Peilung 13,9 sm, bei der zweiten 10,65 sm. Nun kann man zwei beobachtete Orte in die Karte eintragen: es sind dies die Schnittpunkte der Peilung zur Tonne mit den beiden Abstandskreisen. Die Unsicherheit ist in der Geschwindigkeitsmessung begründet.
Verfahren mit dem Rechenschieber
Nach dem obigen Schema würde man mit dem Taschenrechner rechnen. Der mit dem Rechenschieber geübte Navigator erinnert sich an die andere Form des Sinusatzes:
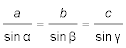 ,
,
oder in Worten:
"Die Seiten eines schiefwinkligen Dreiecks verhalten sich wie die Sinuswerte der den Seiten gegenüberliegenden Winkel."
Bei solchen Proportionalitäten spielt der Rechenschieber seine Vorteile aus: mit einer Einstellung der Zunge und Verschieben des Läufers erhält man alle gewünschten Werte.
Hat man die beiden Deckspeilungen β = 50° (1. Peilung) und γ = 95° (2. Peilung) (und daraus den dritten Winkel α = 35°, der der Seite a gegenüberliegt), und die Entfernung a = 8 sm, so stellt man den Läuferstrich über α = 35° auf der Sinusskala S und die versegelte Strecke a auf der Zungenskala C unter den Läuferstrich (in unserem Beispiel müssen wir noch die Zunge "durchschiebe", d. h. wir verschieben den Läufer auf die "1" der Skala C und verschieben die Zunge damit die "10" am anderen Ende der Skala unter dem Strich steht). Jetzt braucht man nur noch den Läufer nach einander auf die Winkel β und γ zu verschieben, und kann auf der Skala C direkt die Entfernung zum Objekt bei der ersten und der zweiten Peilung ablesen: zur ersten Peilung β = 50° gehört die 2. Entfernung b = 10,68 sm, zur zweiten Peilung sin γ = sin 95° = sin 85° gehört die erste Entfernung c = 13,85 sm.
Die Geschwindigkeit, mit der diese Rechnung möglich ist, sollte ein Taschenrechner einmal nachmachen!
Vierstrichpeilung, Verdoppelungspeilung
Eine Variante der Versegelungspeilung ist die Vierstrichpeilung. Bei ihrer Anwendung nutzt man die Eigenschaften des gleichschenkligen Dreiecks aus. Sie hat den Vorteil, dass man das Ergebnis im Kopf ausrechnen kann, und den Nachteil, dass man längere Zeit peilen muss, um den richtigen Zeitpunkt zu erwischen.
In diesem Abschnitt wird unter "Peilung" immer die Deckspeilung verstanden, d. h. der Peilwinkel bezogen auf die Bootslängsachse!
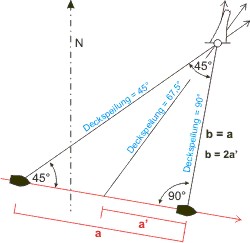
Im gleichschenkligen Dreieck gilt: zwei Seiten sind gleichlang, und die diesen anliegenden Winkel sind gleich. Ist das Dreieck zudem rechtwinklig, betragen die beiden der dritten Seite anliegenden Winkel 45° (weil die Winkelsumme im Dreieck 180° beträgt). Peilt man nun ein Objekt unter 45°, und segelt bis man es querab (unter 90°) sieht, dann entspricht die versegelte Strecke der Entfernung zum Objekt am Ort der 90°-Peilung. (Durch die beiden Peilwinkel wird ein gleichschenkliges Dreieck definiert!) Der Name Vierstrichpeilung stammt aus der Zeit der großen Segler. Damals war der Kompass nicht in 360 Grad, sondern in 32 Striche eingeteilt. Jeder Strich entspricht 11,25°, und 45° sind entsprechend 4 Striche. Man segelt also unter konstantem Kurs mit konstanter Geschwindigkeit und stoppt die Zeit, die man zwischen der 45°-Peilung und der 90°-Peilung benötigt, rechnet mit dem Rechenschieber die Fahrtstrecke aus, und hat zur Peilung noch die Entfernung, also zwei Standlinien deren Schnittpunkt den Schiffsort definieren.
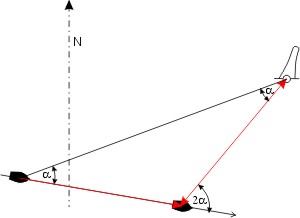
Die Eigenschaft des gleichschenkligen Dreiecks kann man zur "Peilungsverdopplung" ausnutzen: immer, wenn der zweite Peilwinkel genau doppelt so groß ist wie der der ersten Peilung, ist die Entfernung zum Peilobjekt zur Zeit der zweiten Peilung genau gleich der seit der ersten versegelten Strecke. Denn der Innenwinkel im Dreieck, der zu dem Außenwinkel 2 · α gehört beträgt 180° - 2 · α, der dritte Winkel am Objekt ist also
- 180° - 2 · α - (180° - 2 · α) -2 α = α
⇒ das Dreieck muß gleichschenklig sein, denn zwei Winkel sind gleich. Das Problem der Abstandsmessung reduziert sich auf eine Zeitmessung (wenn die Geschwindigkeit konstant war)! Den Rechenschieber braucht man nur noch, um die Fahrstrecke aus der Fahrtzeit und der Geschwindigkeit zu berechnen.
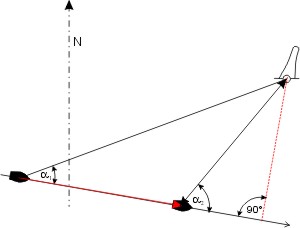
Gelegentlich kann es interessant sein, durch Peilung festzustellen, in welcher Entfernung man ein Hinderniss, z. B. ein Kap, querab passieren wird, ohne in der Karte Standorte und Kurse einzuzeichnen. Dazu gibt es Tabellen von Peilungs-Winkelpaaren, bei denen die Dwarsentfernung im Zusammenhang mit der versegelten Strecke steht.
Man unterscheidet Winkelpaare, für die die versegelte Strecke gleich it der Querab-Entfernung, und solche, für die die Dwarsentfernung ein Bruchteil der Versegelung ist. Hier unten stehen Beispeile. Mit der trigonometrischen Ableitung kann man leicht zusätzliche Winkelpaare finden.
| Erste Peilung | Zweite Peilung |
|
|
|
| 22° | 34° |
| 25° | 41° |
| 27° | 46° |
| 29° | 51° |
| 32° | 59° |
| 40° | 79° |
| 44° | 88° |
| 45° | 90° |
|
|
|
| Erste Peilung | Zweite Peilung | querab Entfernung |
| 22,5° | 45° | 7 ⁄ 10 der Versegelung |
| 30° | 60° | 7 ⁄ 8 der Versegelung |
Trigonometrischen Erklärung
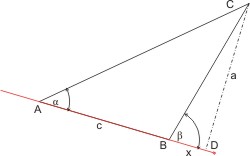
Das Schiff segelt auf der roten Linie. Am Ort A wird das Objekt C unter dem Winkel α, und nach einer Fahrt von A nach B (AB = c) am Ort B unter dem Winkel β gepeilt. Gefragt ist die querab Entfernung a vom Objekt C. (Die Strecke CD = a ist das Lot auf den Kurs des Schiffs.) Wir erkennen zwei rechtwinklige Dreiecke: ADC und BDC, und können mit der Definition der Winkelfunktionen die beiden Gleichungen formulieren:
Aus der zweiten Formel erhält man: x = a ⁄ tan β und kann x in der ersten Formel substituieren:
- a = (c + x) · tan α = (c + a ⁄ tan β) · tan α
Da uns nur der Fall interessiert wo die versegelte Strecke a gleich der Dwarsentfernung a ist, können wir die Gleichung in der Form betrachten:
- a = a · tan α + a · tan α ⁄ tan β
- 1 = tan α · (1 + 1 ⁄ tan β)
Weil diese Gleichung umständlich zu berechnen ist, formt man um:
Diese Gleichung ist transzendent, d. h. man kann sie nicht lösen — wie die Kepler-Gleichung. Man muss iterativ die Paare von α und β suchen, für die tan α · tan β ⁄ (tan β - tan α) = 1 ist, wenn die Versegelung c gleich dem Dwarsabstand a sein soll.
Man kann die Wertepaare der obigen Tabellen leicht mit MS® Excel® nachprüfen (und natürlich weitere Paare finden):
| α | β | Faktor a ⁄ c |
| 22° | 34° | 1,0 |
| 25° | 41° | 1,0 |
| 27° | 46° | 1,0 |
| 29° | 51° | 1,0 |
| 32° | 59° | 1,0 |
| 40° | 79° | 1,0 |
| 44° | 88° | 1,0 |
| 45° | 90° | 1,0 |
| 22,5° | 45° | 0,7 = 7 ⁄ 10 |
| 30° | 60° | 0,9 = 7 ⁄ 8 |
Quellen:
- Squire Thornton Stratford Lecky: Wrinkles in Practical Navigation, London (1894).
- Squire Thornton Stratford Lecky: The Danger Tables and Off-Shore Distance Tables. London (1882).
- Lehrbuch der Navigation, Reichs-Marine-Amt (Herausg.), Berlin 1906.
- Nathaniel Bowditch: The American Practical Navigator, Bethesda 2002.
© Rainer Stumpe, URL: www.rainerstumpe.de/
Datenschutzerklärung